随机事件的概率(广东省珠海市)
图片预览






文档简介
课件18张PPT。随机事件的概率 一.知识要点 (3)随机事件:在一定的条件下可能发生也可能不发生的事件.用大写字母A、B、C、D…表示. (1).在条件S下,一定会发生的事件,叫必然事件;(2).在条件S下,一定不会发生的事件,叫不可能事件; 1.三类事件必然事件和不可能事件统称为相对于条件S的确定事件. (1)频率:在相同条件S下,重复进行n次试验,事件A出现的次数nA叫事件A出现的频数,比值fn(A)=nA/n称为事件A出现的频率。2.随机事件的概率 (2)概率:对于给定的随机事件A,如果 随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作
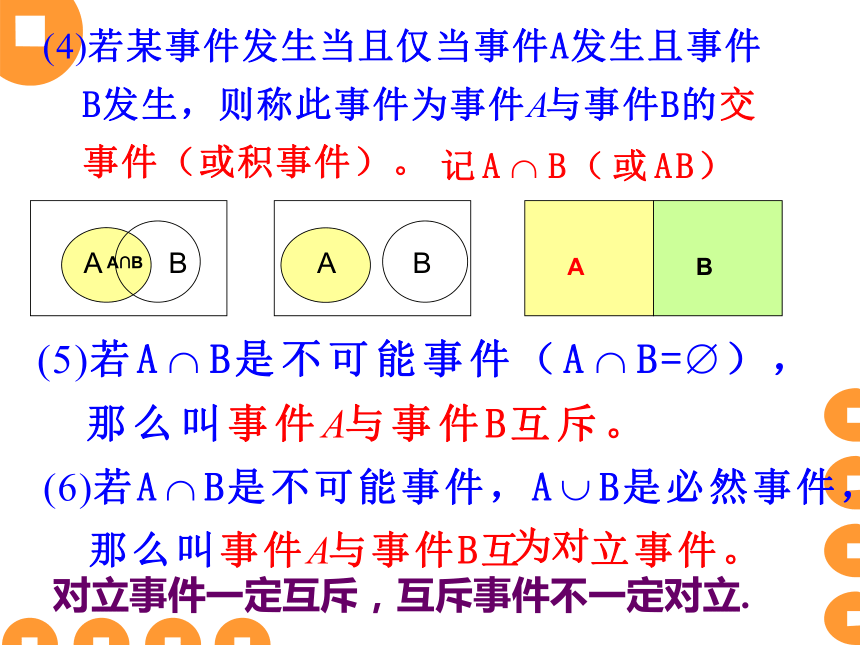
P(A),称为事件A的概率。3.事件的关系与运算注:为对对立事件一定互斥,互斥事件不一定对立. 4.概率的基本性质:
(1)0≤P(A)≤1
(2)若事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)
(3)若事件A与事件B为对立事件,则
P(A∪B)=P(A)+P(B)=1 1、指出下列事件哪些是必然事件,不可能事件,随机事件?
(1)三角形的内角和为180度;
(2)种子在水分充足的条件下发芽;
(3)方程x2+2x+3=0有两个实根;
二.例题分析 必然随机不可能2.从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是 ( )
A、“至少有一个红球”与“都是红球”
B、“至少有一个红球”与“都是白球”
C、“至少有一个红球”与“至少有一个白球”
D、“恰有一个红球”与“恰有二个红球”D 3.甲、乙两人下棋,和棋的概率为1/2,乙获胜的概率为1/3,求:
(1)甲获胜的概率;
(2)甲不输的概率. 4.袋中有12个相同大小的小球,分别为红球、黑球、黄球和绿球,从中任取一球,得到红球的概率为1/3,得到黑球或黄球的概率为5/12,得到黄球或绿球的概率也是5/12
(1)求得到黑球,黄球和绿球的概率各是多少?
(2)求得到的不是黑球也不是绿球的概率.5.某射击运动员射击一次射中10环、9环、8环、
7环的概率分别是0.24、0.28、0.19、0.16,计算这名运动员射击一次
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不超过7环的概率。
掷一枚质地均匀的骰子的试验,可能出现几种不同的结果? 像上面出现的“1点”、 “2点”、 “3点”、 “4点”、 “5点”、 “6点”这些随机事件叫做构成试验结果的基本事件。在一次实验中,可能出现的不能再分的最简单的基本结果构成的事件叫基本事件.而其它事件都可用基本事件
来表示. 1、基本事件 从字母a、b、c、d中任意取出两个不同字母的试验中,有哪些基本事件?解:所求的基本事件共有6个:A={a, b} B={a, c} C={a, d} D={b, c} E={b, d} F={c, d} 练习(1)有限性:在随机试验中,其可能出现的结果有有限个,即只有有限个不同的基本事件;(2)等可能性:每个基本事件发生的机会是均等的。有两个特征:2.古典概型 一般地,对于古典概型,如果一次试验中所有基本事件共有n个,那么每一个基本事件发生的概率都是1/n;如果某个事件A所包含的基本事件数为m,那么事件A的概率为3.古典概率的计算方法:
2.特点
(1)试验中所有可能出现的基本事件为无限个;
(2)每一个基本事件发生的可能性都相等。几何概型的概念和特点1.概念
如果每个事件发生的概率只与构成 该事件区域的长度(面积、体积)成比例,则称这样的概率模型为几何概率摸型,简称几何概型.3.几何概型中,事件A的概率的计算公式
4.古典概型与几何概型的区别
相同点:每一个基本事件出现的可能性都相等。
不同点 :古典概型中基本事件为有限个;几何概型中基本事件为无限个.3.用橡皮泥做成一个直径为6cm的小球,假设橡皮泥中
混入了一个很小的砂粒,则这个砂粒距离球心不小于1cm
的概率是______.2.向边长为2的正方形内随机投一粒豆子,则豆子到
正方形的各顶点的距离均大于1的概率是______.1. 已知在△ABC中,∠B=90oAB=4,AC=5,BC=3,,
点D为AC上一点,求△BDC为锐角三角形的概率.
P(A),称为事件A的概率。3.事件的关系与运算注:为对对立事件一定互斥,互斥事件不一定对立. 4.概率的基本性质:
(1)0≤P(A)≤1
(2)若事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)
(3)若事件A与事件B为对立事件,则
P(A∪B)=P(A)+P(B)=1 1、指出下列事件哪些是必然事件,不可能事件,随机事件?
(1)三角形的内角和为180度;
(2)种子在水分充足的条件下发芽;
(3)方程x2+2x+3=0有两个实根;
二.例题分析 必然随机不可能2.从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是 ( )
A、“至少有一个红球”与“都是红球”
B、“至少有一个红球”与“都是白球”
C、“至少有一个红球”与“至少有一个白球”
D、“恰有一个红球”与“恰有二个红球”D 3.甲、乙两人下棋,和棋的概率为1/2,乙获胜的概率为1/3,求:
(1)甲获胜的概率;
(2)甲不输的概率. 4.袋中有12个相同大小的小球,分别为红球、黑球、黄球和绿球,从中任取一球,得到红球的概率为1/3,得到黑球或黄球的概率为5/12,得到黄球或绿球的概率也是5/12
(1)求得到黑球,黄球和绿球的概率各是多少?
(2)求得到的不是黑球也不是绿球的概率.5.某射击运动员射击一次射中10环、9环、8环、
7环的概率分别是0.24、0.28、0.19、0.16,计算这名运动员射击一次
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不超过7环的概率。
掷一枚质地均匀的骰子的试验,可能出现几种不同的结果? 像上面出现的“1点”、 “2点”、 “3点”、 “4点”、 “5点”、 “6点”这些随机事件叫做构成试验结果的基本事件。在一次实验中,可能出现的不能再分的最简单的基本结果构成的事件叫基本事件.而其它事件都可用基本事件
来表示. 1、基本事件 从字母a、b、c、d中任意取出两个不同字母的试验中,有哪些基本事件?解:所求的基本事件共有6个:A={a, b} B={a, c} C={a, d} D={b, c} E={b, d} F={c, d} 练习(1)有限性:在随机试验中,其可能出现的结果有有限个,即只有有限个不同的基本事件;(2)等可能性:每个基本事件发生的机会是均等的。有两个特征:2.古典概型 一般地,对于古典概型,如果一次试验中所有基本事件共有n个,那么每一个基本事件发生的概率都是1/n;如果某个事件A所包含的基本事件数为m,那么事件A的概率为3.古典概率的计算方法:
2.特点
(1)试验中所有可能出现的基本事件为无限个;
(2)每一个基本事件发生的可能性都相等。几何概型的概念和特点1.概念
如果每个事件发生的概率只与构成 该事件区域的长度(面积、体积)成比例,则称这样的概率模型为几何概率摸型,简称几何概型.3.几何概型中,事件A的概率的计算公式
4.古典概型与几何概型的区别
相同点:每一个基本事件出现的可能性都相等。
不同点 :古典概型中基本事件为有限个;几何概型中基本事件为无限个.3.用橡皮泥做成一个直径为6cm的小球,假设橡皮泥中
混入了一个很小的砂粒,则这个砂粒距离球心不小于1cm
的概率是______.2.向边长为2的正方形内随机投一粒豆子,则豆子到
正方形的各顶点的距离均大于1的概率是______.1. 已知在△ABC中,∠B=90oAB=4,AC=5,BC=3,,
点D为AC上一点,求△BDC为锐角三角形的概率.
