江苏省徐州市铜山区黄集镇中心中学2023-2024学年八年级上学期第一次质量检测数学试卷(无答案)
文档属性
| 名称 | 江苏省徐州市铜山区黄集镇中心中学2023-2024学年八年级上学期第一次质量检测数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 556.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 11:08:42 | ||
图片预览

文档简介
2023—2024学年度第一学期八数第一次学情调研
题号 1 2 3 4 5 6 7 8 9 10
选项
一、选择题(10×3=30分)
1.下列各组中的两个图形属于全等形的是( )
A. B. C. D.
2.下列美丽的图案中是轴对称图形的个数有( )
A.1 个 B.2 个 C.3 个 D.4 个
3.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是带 ( )去 A ③ B ② C ① D ① ②
4. 如图,△ABC≌△EDF,AE=20,FC=10,则AF的长是( )
A . 5 B. 10 C. 15 D. 不能确定
第3题 第4题 第5题 第6题
5.用尺规作一个角平分线的示意图如图所示,则说明∠AOC=∠BOC相等的依据 ( )
A SAS B ASA C AAS D SSS
6.如图,AC、BD 相交于点 O,OA=OD,用“SAS”证△ABO≌△DCO还需( )
A.AB=DC B.∠A=∠D C.OB=OC D.∠AOB=∠DOC
7.到三角形的三个顶点距离相等的点是三角形( )
A. 三条中线的交点 B.三条角平分线的交点
C.三条边的垂直平分线的交点 D.三条高的交点
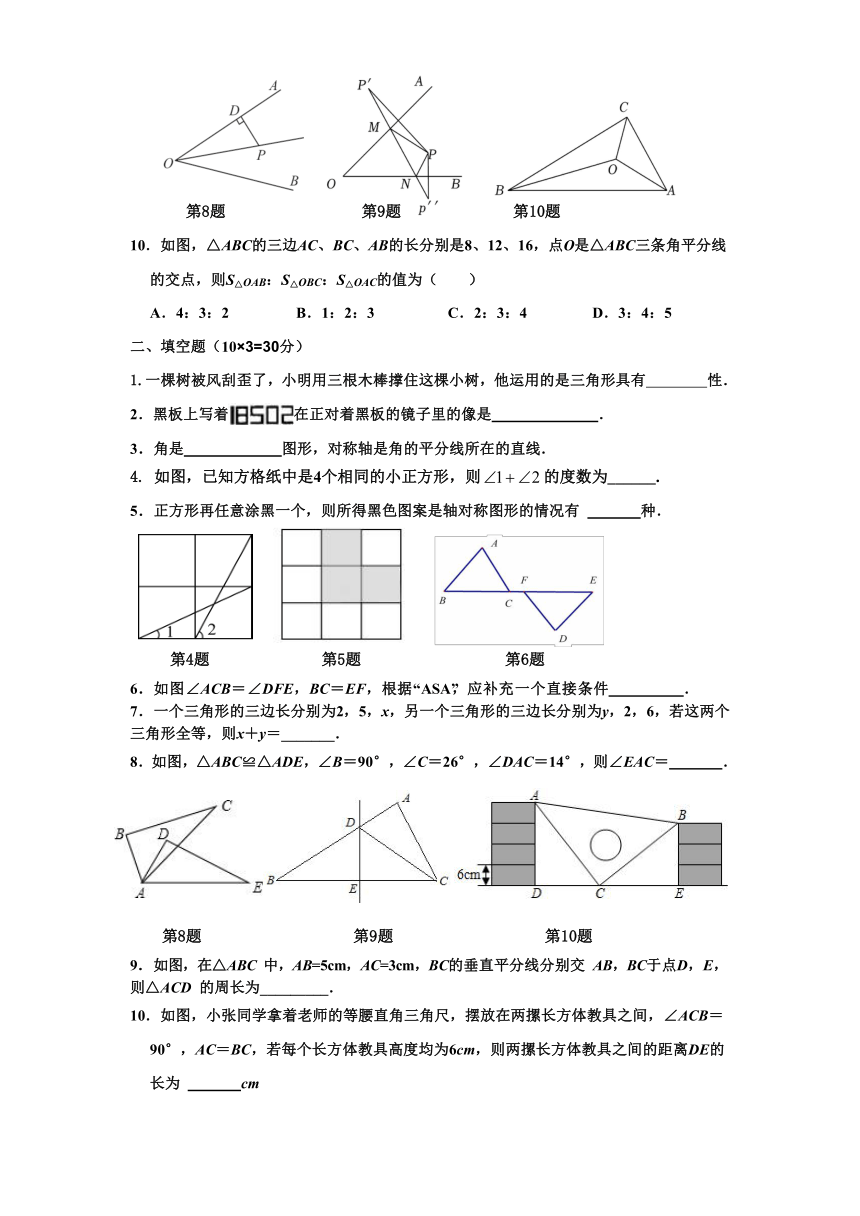
8. 如图,OP平分∠AOB,PD⊥OA于点D,点Q是射线OB上一个动点.若PD=5,则PQ的最小值为( )
B. C. D. 以上情况都有可能
9. 如图,点P是∠AOB内部一点,点P′,P″分别是点P关于OA,OB的对称点,
且P′P″=8cm,则△PMN的周长为( )
A.5cm B.6cm C.7cm D.8cm
第8题 第9题 第10题
10.如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.1:2:3 C.2:3:4 D.3:4:5
二、填空题(10×3=30分)
1.一棵树被风刮歪了,小明用三根木棒撑住这棵小树,他运用的是三角形具有 性.
2.黑板上写着在正对着黑板的镜子里的像是 .
3.角是 图形,对称轴是角的平分线所在的直线.
4. 如图,已知方格纸中是4个相同的小正方形,则的度数为______.
5.正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有 种.
第4题 第5题 第6题
6.如图∠ACB=∠DFE,BC=EF,根据“ASA”,应补充一个直接条件 .
7.一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6,若这两个三角形全等,则x+y=_______.
8.如图,△ABC≌△ADE,∠B=90°,∠C=26°,∠DAC=14°,则∠EAC= .
第8题 第9题 第10题
9.如图,在△ABC 中,AB=5cm,AC=3cm,BC的垂直平分线分别交 AB,BC于点 D,E,则△ACD 的周长为_________.
10.如图,小张同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间,∠ACB=90°,AC=BC,若每个长方体教具高度均为6cm,则两摞长方体教具之间的距离DE的长为 cm
三、作图题(8+6=14分)
1.如图,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等。
(
A
O
D
C
B
)
(2)作出△ABC关于直线L的轴对称△A′B′C′.
(
L
)
四、解答题(8+8+8+10+12=46分)
1.已知,∠1=∠2,∠B=∠C,AB=AC.求证:∠D=∠E.
2.如图,AC、BD 相交于点 O,且 AB=DC,AC=DB.求证:∠A=∠D.
3. 已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.
4.△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.
求证:AD垂直平分EF.
5. 如图所示CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE、BD,AE与BD交于点P.
(1)求证:AE=BD;
(2)如果∠ACD=35°,那么∠DPE=___________;
(3)连接PC,猜想并证明∠APC与∠BPC的关系.
题号 1 2 3 4 5 6 7 8 9 10
选项
一、选择题(10×3=30分)
1.下列各组中的两个图形属于全等形的是( )
A. B. C. D.
2.下列美丽的图案中是轴对称图形的个数有( )
A.1 个 B.2 个 C.3 个 D.4 个
3.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是带 ( )去 A ③ B ② C ① D ① ②
4. 如图,△ABC≌△EDF,AE=20,FC=10,则AF的长是( )
A . 5 B. 10 C. 15 D. 不能确定
第3题 第4题 第5题 第6题
5.用尺规作一个角平分线的示意图如图所示,则说明∠AOC=∠BOC相等的依据 ( )
A SAS B ASA C AAS D SSS
6.如图,AC、BD 相交于点 O,OA=OD,用“SAS”证△ABO≌△DCO还需( )
A.AB=DC B.∠A=∠D C.OB=OC D.∠AOB=∠DOC
7.到三角形的三个顶点距离相等的点是三角形( )
A. 三条中线的交点 B.三条角平分线的交点
C.三条边的垂直平分线的交点 D.三条高的交点
8. 如图,OP平分∠AOB,PD⊥OA于点D,点Q是射线OB上一个动点.若PD=5,则PQ的最小值为( )
B. C. D. 以上情况都有可能
9. 如图,点P是∠AOB内部一点,点P′,P″分别是点P关于OA,OB的对称点,
且P′P″=8cm,则△PMN的周长为( )
A.5cm B.6cm C.7cm D.8cm
第8题 第9题 第10题
10.如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.1:2:3 C.2:3:4 D.3:4:5
二、填空题(10×3=30分)
1.一棵树被风刮歪了,小明用三根木棒撑住这棵小树,他运用的是三角形具有 性.
2.黑板上写着在正对着黑板的镜子里的像是 .
3.角是 图形,对称轴是角的平分线所在的直线.
4. 如图,已知方格纸中是4个相同的小正方形,则的度数为______.
5.正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有 种.
第4题 第5题 第6题
6.如图∠ACB=∠DFE,BC=EF,根据“ASA”,应补充一个直接条件 .
7.一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6,若这两个三角形全等,则x+y=_______.
8.如图,△ABC≌△ADE,∠B=90°,∠C=26°,∠DAC=14°,则∠EAC= .
第8题 第9题 第10题
9.如图,在△ABC 中,AB=5cm,AC=3cm,BC的垂直平分线分别交 AB,BC于点 D,E,则△ACD 的周长为_________.
10.如图,小张同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间,∠ACB=90°,AC=BC,若每个长方体教具高度均为6cm,则两摞长方体教具之间的距离DE的长为 cm
三、作图题(8+6=14分)
1.如图,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等。
(
A
O
D
C
B
)
(2)作出△ABC关于直线L的轴对称△A′B′C′.
(
L
)
四、解答题(8+8+8+10+12=46分)
1.已知,∠1=∠2,∠B=∠C,AB=AC.求证:∠D=∠E.
2.如图,AC、BD 相交于点 O,且 AB=DC,AC=DB.求证:∠A=∠D.
3. 已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.
4.△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.
求证:AD垂直平分EF.
5. 如图所示CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE、BD,AE与BD交于点P.
(1)求证:AE=BD;
(2)如果∠ACD=35°,那么∠DPE=___________;
(3)连接PC,猜想并证明∠APC与∠BPC的关系.
同课章节目录
