第一单元圆应用题拔高篇(专项训练)数学六年级上册北师大版(含答案)
文档属性
| 名称 | 第一单元圆应用题拔高篇(专项训练)数学六年级上册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 09:19:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一单元圆应用题拔高篇(专项训练)数学六年级上册北师大版
1.有一个直径为1m的圆形洞口,一个身高为1.45m的小女孩不能直身过去.如果这个洞口周长增加1.57m,请你计算小女孩能直身通过吗?
2.下图是一个长10dm、宽4dm的长方形塑料板.现在要把它裁剪成一个最大的半圆,并在周围包上金属条,至少需要多少分米的金属条?(接头处忽略不计)
3.右图是两个大小不同互相咬合的齿轮,大齿轮的半径是18 cm,小齿轮的半径是6 cm,大齿轮转动2周,小齿轮要转动几周
4.如图,中间是边长为1分米的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形,这个图形的周长是多少分米?
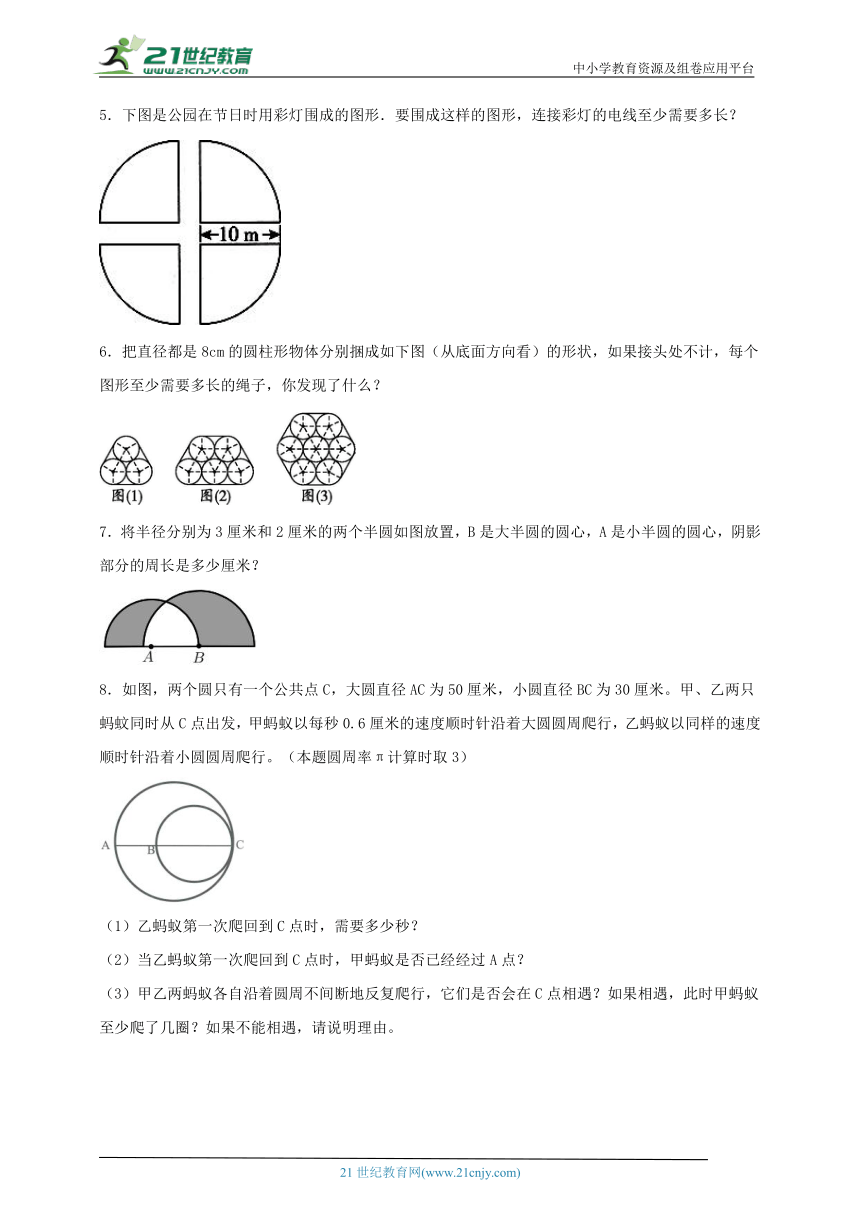
5.下图是公园在节日时用彩灯围成的图形.要围成这样的图形,连接彩灯的电线至少需要多长?
6.把直径都是8cm的圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每个图形至少需要多长的绳子,你发现了什么?
7.将半径分别为3厘米和2厘米的两个半圆如图放置,B是大半圆的圆心,A是小半圆的圆心,阴影部分的周长是多少厘米?
8.如图,两个圆只有一个公共点C,大圆直径AC为50厘米,小圆直径BC为30厘米。甲、乙两只蚂蚊同时从C点出发,甲蚂蚁以每秒0.6厘米的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(本题圆周率π计算时取3)
(1)乙蚂蚁第一次爬回到C点时,需要多少秒?
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过A点?
(3)甲乙两蚂蚁各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,此时甲蚂蚁至少爬了几圈?如果不能相遇,请说明理由。
9.脱粒用的电动机的传动轮直径为0.16米 ,脱粒机的转动轮直径为0.24米,若电动机每分钟转3600转,则脱粒机的转动轮每分钟转多少转
10.如图,有一只狗被拴在一建筑物的墙角A点上,这个建筑物的底面是边长为6米的正方形,拴狗的绳长15米,现在狗从B点出发,将绳拉紧并沿顺时针跑,狗最多可跑多少米?
11.下图中,大圆半径是10厘米,起始位置如图,如果小圆从A点沿大圆内侧滚动至B点,请在下图中画出小圆圆心走过的轨迹,并计算小圆圆心走过的路线是多少厘米?
12.如图是一幅钟面的示意图,图中的阴影部分是一个近似的梯形。已知钟面直径是24厘米,则这个近似梯形的面积是多少平方厘米?
13.如下图,已知圆外面正方形的面积是15平方分米,则阴影部分的面积是多少平方分米?
14.下图是一个边长6分米的正方形,在里面有一个半径是10厘米的圆,圆沿正方形边长内侧滚动一周。
(1)求圆滚动的距离。
(2)这个圆滚不到部分的面积是多少?
15.如图BC=12cm,CD=DE=6cm,①与②两阴影部分的面积的差(较大的减去较小的)是多少?
16.图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD为直径画半圆,求这四个半圆弧所围成的阴影部分的面积。
参考答案:
1.能
【详解】(3.14×1+1.57)÷3.14=1.5(m)
1.5>1.45
能
2.20.56dm
【分析】在长方形上裁剪最大的半圆与在长方形上裁剪最大的圆考虑方向截然不同:裁剪最大的圆只能以宽为直径.圆才不会超出长方形;而裁剪最大的半圆,先考虑长能不能作直径,如果不行,再考虑宽作半径.本题如果以长作直径,宽的长度不够,只能以宽作半径,所以就裁剪成下图的形状,再计算这个半圆的周长.
【详解】2×3.14×4÷2+4×2=20.56(dm)
答:至少需要20.56dm的金属条.
3.18÷6×2=6(周)
【详解】略
4.10.28分米
【分析】由题意知:图形的周长=4个圆弧的长度(也就是一个圆的周长)+4条圆的半径(边长1分米的正方形的边长)
【详解】3.14×2×1+1×4
=6.28+4
=10.28(分米)
答:这个图形的周长是10.28分米。
【点睛】解答此题关键是弄清楚,这个图形由哪些图形组成,利用规则图形的周长和,即可得解。
5.142.8m
【详解】10×2×3.14+10×8=142.8(m)
答:连接彩灯的电线至少需要142.8m.
6.见详解
【分析】通过观察图形可知,图1的绳子长度=一个圆的周长+3条直径长,图2绳子的长度=一个圆的周长+5条直径长,图3绳子的长度=一个圆的周长+6条直径长,由此分别求出绳子的长度。
【详解】8×3+3.14×8
=24+25.12
=49.12(cm)
8×5+3.14×8
=40+25.12
=65.12(cm)
8×6+3.14×8
=48+25.12
=73.12(cm)
答:图1绳子长49.12厘米,图2绳子长65.12厘米,图3绳子长73.12厘米。
发现:最少需要绳子的长度等于一个圆的周长加上若干条直径的和。最外圈有几个圆柱形物体,就有几条直径。
【点睛】解答此题需要先认真观察分析图形,找出内在的规律进而解答。
7.19.7厘米
【分析】观察图形可知,阴影部分的周长就是这个半径为3厘米和2厘米的半圆的弧长,再加上大半圆的半径3厘米与小半圆的直径减去大半圆的半径的差,据此利用圆的周长公式分别求出这两个半圆的弧长即可解答问题。
【详解】3.14×3×2÷2+3.14×2×2÷2+3+2×2-3
=9.42+6.28+3+1
=19.7(厘米)
答:阴影部分的周长是19.7厘米。
【点睛】考查了圆的周长公式的灵活运用,本题的关键是得到阴影部分的周长=2个半圆的弧长+下面两条直线段的长度之和。
8.(1)150秒;(2)没有;(3)会,3圈
【分析】(1)根据圆的周长C=πd,先求出小圆的周长,再除以乙蚂蚁的速度即可;
(2)根据圆的周长C=πd,先求出大圆的周长,再除以甲蚂蚁的速度,求出甲蚂蚁用的时间,与乙蚂蚁爬行一周用的时间比较即可;
(3)先求出甲蚂蚁和乙蚂蚁爬一圈所用时间的最小公倍数,再除以甲蚂蚁爬一圈用的时间即可。
【详解】(1)3×30÷0.6
=90÷0.6
=150(秒)
答:需要150秒。
(2)3×50÷0.6
=150÷0.6
=250(秒)
250>150
答:还没有到达A点。
(3)150=2×3×5×5
250=2×5×5×5
所以150和250的最小公倍数是2×3×5×5×5=750
750÷250=3(圈)
答:会在C点相遇,此时甲蚂蚁至少爬了3圈。
【点睛】此题考查了圆的周长与最小公倍数的综合应用,掌握公式,认真解答即可。
9.2400转
【详解】0.16×3.14×3600/(0.24×3.14)=2400(转)
10.42.39米
【分析】先分析狗跑过的路径:第一段是半径为15米的圆的周长的;第二段是半径为(15-6)米的圆的周长的;第三段是半径为(15-6-6)米的圆的周长的;把这三段路程相加即可。
【详解】如图:
3.14×15×2×
=47.1×2×
=94.2×
=23.55(米)
3.14×(15-6)×2×
=3.14×9×2×
=28.26×2×
=56.52×
=14.13(米)
3.14×(15-6-6)×2×
=3.14×3×2×
=9.42×2×
=18.84×
=4.71(米)
23.55+14.13+4.71
=37.68+4.71
=42.39(米)
答:狗最多可跑42.39米。
【点睛】解决此题的关键是找到圆的半径。
11.图见详解;15.7厘米
【分析】由题意可知:小圆圆心走过的轨迹是以点O为圆心,半径是10÷2=5厘米的圆的一半;将数据代入圆的周长公式计算即可。
【详解】作图如下:
3.14×(10÷2)×2÷2
=3.14×5
=15.7(厘米)
答:小圆圆心走过的路线是15.7厘米。
【点睛】本题主要考查圆的周长公式的灵活运用,明确圆心的轨迹是解题的关键。
12.75.36平方厘米
【分析】由图可知,虚线将上面半圆分成了两部分,左边是右边的2倍,左边比右边多的恰好是阴影部分的面积,据此解答。
【详解】3.14×(24÷2)2÷2÷3×(2-1)
=3.14×144÷6
=3.14×24
=75.36(平方厘米)
答:这个近似梯形的面积是75.36平方厘米。
【点睛】明确半圆部分虚线左边比右边多的面积恰好就是阴影部分的面积是解决此题的关键。
13.4.275平方分米
【分析】根据题意可知,先设圆的半径为r,然后用r表示大正方形的面积,再根据大正方形的面积求出圆的面积,里面正方形的面积等于以圆的直径为底,圆的半径为直角边的四个三角形的面积之和,再根据阴影部分的面积=圆面积-小正方形面积得解。
【详解】设圆的半径为r
大正方形的面积=2r×2r=15
则r2=
圆的面积=πr2=3.14×=11.775(平方分米)
小正方形的面积=r×r÷2×4=7.5(平方分米)
阴影部分的面积=11.775-7.5=4.275(平方分米)
答:阴影部分的面积是4.275平方分米。
【点睛】解决本题的关键是将里面的正方形面积转化成两个三角形的面积,利用半径的平方,代入关系式再计算。
14.(1)222.8厘米
(2)486平方厘米
【分析】如下图所示:
(1)圆沿正方形边长内侧滚动一周的距离就是四个角上的圆弧长度与四条边上的线段之和。4个圆弧组成整圆,根据圆的周长=2πr求出整圆的周长,四条边上的线段都是正方形的边长减去圆的两个半径的长度,最后把两者加起来。
(2)圆滚不到的面积是四个角上的阴影部分面积和中间的小正方形的面积之和。四个阴影部分是用角上的小正方形的面积减去扇形的面积,根据正方形的面积=边长×边长、圆的面积=π解答。
【详解】(1)6分米=60厘米
3.14×10×2+(60-10-10)×4
=62.8+160
=222.8(厘米)
答:圆滚动的距离是222.8厘米。
(2)中间小正方形的边长:60-10×4
=60-40
=20(厘米)
(10×10-3.14××)×4+20×20
=(100-78.5)×4+400
=21.5×4+400
=86+400
=486(平方厘米)
答:这个圆滚不到部分的面积是486平方厘米。
【点睛】本题考查有关圆的组合图形的周长和面积运算,理解问题的具体所求是解题的关键。
15.12.78cm2
【分析】如下图所示,用③表示一块阴影部分的面积,则①-②=(①+③)-(②+③)。用半径是12cm的大扇形的面积减去半径是6cm的小扇形的面积即可得出①与③两阴影部分的面积之和,而②与③两阴影部分的面积之和等于长方形的面积,那么用大扇形的面积减去小扇形的面积,再减去长方形的面积,即可求出①与②两阴影部分的面积的差。图中扇形的面积是整圆面积的,根据S=πr2求出整圆面积,再除以4分别求出两个扇形的面积;根据长方形的面积=长×宽,求出长方形的面积。最后根据上面的分析结果进行解答。
【详解】
=3.14×27-72
(cm2)
答:①与②两阴影部分的面积的差是12.78cm2。
【点睛】把①与②两阴影部分的面积的差,转化为①与③的面积之和,与②与③面积之和的差,是解题的关键。再运用圆的面积公式和长方形的面积公式分别求出两部分的面积。
16.9.12平方米
【分析】如下图所示,分别连接点A、点B和半圆的交点,则两条虚线组成一个三角形,用半圆的面积减去三角形的面积,即求出阴影部分的面积。再乘4求出整个阴影部分的面积。根据圆的面积=π,三角形的面积=底×高÷2,即可解答。
【详解】半径:4÷2=2(米)
阴影部分的面积:3.14×÷2-4×2÷2
=3.14×4÷2-4
=6.28-4
=2.28(平方米)
整个阴影部分的面积:2.28×4=9.12(平方米)
【点睛】通过添加辅助线,用半圆的面积减去三角形的面积求出阴影部分的面积是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一单元圆应用题拔高篇(专项训练)数学六年级上册北师大版
1.有一个直径为1m的圆形洞口,一个身高为1.45m的小女孩不能直身过去.如果这个洞口周长增加1.57m,请你计算小女孩能直身通过吗?
2.下图是一个长10dm、宽4dm的长方形塑料板.现在要把它裁剪成一个最大的半圆,并在周围包上金属条,至少需要多少分米的金属条?(接头处忽略不计)
3.右图是两个大小不同互相咬合的齿轮,大齿轮的半径是18 cm,小齿轮的半径是6 cm,大齿轮转动2周,小齿轮要转动几周
4.如图,中间是边长为1分米的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形,这个图形的周长是多少分米?
5.下图是公园在节日时用彩灯围成的图形.要围成这样的图形,连接彩灯的电线至少需要多长?
6.把直径都是8cm的圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每个图形至少需要多长的绳子,你发现了什么?
7.将半径分别为3厘米和2厘米的两个半圆如图放置,B是大半圆的圆心,A是小半圆的圆心,阴影部分的周长是多少厘米?
8.如图,两个圆只有一个公共点C,大圆直径AC为50厘米,小圆直径BC为30厘米。甲、乙两只蚂蚊同时从C点出发,甲蚂蚁以每秒0.6厘米的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(本题圆周率π计算时取3)
(1)乙蚂蚁第一次爬回到C点时,需要多少秒?
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过A点?
(3)甲乙两蚂蚁各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,此时甲蚂蚁至少爬了几圈?如果不能相遇,请说明理由。
9.脱粒用的电动机的传动轮直径为0.16米 ,脱粒机的转动轮直径为0.24米,若电动机每分钟转3600转,则脱粒机的转动轮每分钟转多少转
10.如图,有一只狗被拴在一建筑物的墙角A点上,这个建筑物的底面是边长为6米的正方形,拴狗的绳长15米,现在狗从B点出发,将绳拉紧并沿顺时针跑,狗最多可跑多少米?
11.下图中,大圆半径是10厘米,起始位置如图,如果小圆从A点沿大圆内侧滚动至B点,请在下图中画出小圆圆心走过的轨迹,并计算小圆圆心走过的路线是多少厘米?
12.如图是一幅钟面的示意图,图中的阴影部分是一个近似的梯形。已知钟面直径是24厘米,则这个近似梯形的面积是多少平方厘米?
13.如下图,已知圆外面正方形的面积是15平方分米,则阴影部分的面积是多少平方分米?
14.下图是一个边长6分米的正方形,在里面有一个半径是10厘米的圆,圆沿正方形边长内侧滚动一周。
(1)求圆滚动的距离。
(2)这个圆滚不到部分的面积是多少?
15.如图BC=12cm,CD=DE=6cm,①与②两阴影部分的面积的差(较大的减去较小的)是多少?
16.图中ABCD是边长为4米的正方形,分别以AB、BC、CD、AD为直径画半圆,求这四个半圆弧所围成的阴影部分的面积。
参考答案:
1.能
【详解】(3.14×1+1.57)÷3.14=1.5(m)
1.5>1.45
能
2.20.56dm
【分析】在长方形上裁剪最大的半圆与在长方形上裁剪最大的圆考虑方向截然不同:裁剪最大的圆只能以宽为直径.圆才不会超出长方形;而裁剪最大的半圆,先考虑长能不能作直径,如果不行,再考虑宽作半径.本题如果以长作直径,宽的长度不够,只能以宽作半径,所以就裁剪成下图的形状,再计算这个半圆的周长.
【详解】2×3.14×4÷2+4×2=20.56(dm)
答:至少需要20.56dm的金属条.
3.18÷6×2=6(周)
【详解】略
4.10.28分米
【分析】由题意知:图形的周长=4个圆弧的长度(也就是一个圆的周长)+4条圆的半径(边长1分米的正方形的边长)
【详解】3.14×2×1+1×4
=6.28+4
=10.28(分米)
答:这个图形的周长是10.28分米。
【点睛】解答此题关键是弄清楚,这个图形由哪些图形组成,利用规则图形的周长和,即可得解。
5.142.8m
【详解】10×2×3.14+10×8=142.8(m)
答:连接彩灯的电线至少需要142.8m.
6.见详解
【分析】通过观察图形可知,图1的绳子长度=一个圆的周长+3条直径长,图2绳子的长度=一个圆的周长+5条直径长,图3绳子的长度=一个圆的周长+6条直径长,由此分别求出绳子的长度。
【详解】8×3+3.14×8
=24+25.12
=49.12(cm)
8×5+3.14×8
=40+25.12
=65.12(cm)
8×6+3.14×8
=48+25.12
=73.12(cm)
答:图1绳子长49.12厘米,图2绳子长65.12厘米,图3绳子长73.12厘米。
发现:最少需要绳子的长度等于一个圆的周长加上若干条直径的和。最外圈有几个圆柱形物体,就有几条直径。
【点睛】解答此题需要先认真观察分析图形,找出内在的规律进而解答。
7.19.7厘米
【分析】观察图形可知,阴影部分的周长就是这个半径为3厘米和2厘米的半圆的弧长,再加上大半圆的半径3厘米与小半圆的直径减去大半圆的半径的差,据此利用圆的周长公式分别求出这两个半圆的弧长即可解答问题。
【详解】3.14×3×2÷2+3.14×2×2÷2+3+2×2-3
=9.42+6.28+3+1
=19.7(厘米)
答:阴影部分的周长是19.7厘米。
【点睛】考查了圆的周长公式的灵活运用,本题的关键是得到阴影部分的周长=2个半圆的弧长+下面两条直线段的长度之和。
8.(1)150秒;(2)没有;(3)会,3圈
【分析】(1)根据圆的周长C=πd,先求出小圆的周长,再除以乙蚂蚁的速度即可;
(2)根据圆的周长C=πd,先求出大圆的周长,再除以甲蚂蚁的速度,求出甲蚂蚁用的时间,与乙蚂蚁爬行一周用的时间比较即可;
(3)先求出甲蚂蚁和乙蚂蚁爬一圈所用时间的最小公倍数,再除以甲蚂蚁爬一圈用的时间即可。
【详解】(1)3×30÷0.6
=90÷0.6
=150(秒)
答:需要150秒。
(2)3×50÷0.6
=150÷0.6
=250(秒)
250>150
答:还没有到达A点。
(3)150=2×3×5×5
250=2×5×5×5
所以150和250的最小公倍数是2×3×5×5×5=750
750÷250=3(圈)
答:会在C点相遇,此时甲蚂蚁至少爬了3圈。
【点睛】此题考查了圆的周长与最小公倍数的综合应用,掌握公式,认真解答即可。
9.2400转
【详解】0.16×3.14×3600/(0.24×3.14)=2400(转)
10.42.39米
【分析】先分析狗跑过的路径:第一段是半径为15米的圆的周长的;第二段是半径为(15-6)米的圆的周长的;第三段是半径为(15-6-6)米的圆的周长的;把这三段路程相加即可。
【详解】如图:
3.14×15×2×
=47.1×2×
=94.2×
=23.55(米)
3.14×(15-6)×2×
=3.14×9×2×
=28.26×2×
=56.52×
=14.13(米)
3.14×(15-6-6)×2×
=3.14×3×2×
=9.42×2×
=18.84×
=4.71(米)
23.55+14.13+4.71
=37.68+4.71
=42.39(米)
答:狗最多可跑42.39米。
【点睛】解决此题的关键是找到圆的半径。
11.图见详解;15.7厘米
【分析】由题意可知:小圆圆心走过的轨迹是以点O为圆心,半径是10÷2=5厘米的圆的一半;将数据代入圆的周长公式计算即可。
【详解】作图如下:
3.14×(10÷2)×2÷2
=3.14×5
=15.7(厘米)
答:小圆圆心走过的路线是15.7厘米。
【点睛】本题主要考查圆的周长公式的灵活运用,明确圆心的轨迹是解题的关键。
12.75.36平方厘米
【分析】由图可知,虚线将上面半圆分成了两部分,左边是右边的2倍,左边比右边多的恰好是阴影部分的面积,据此解答。
【详解】3.14×(24÷2)2÷2÷3×(2-1)
=3.14×144÷6
=3.14×24
=75.36(平方厘米)
答:这个近似梯形的面积是75.36平方厘米。
【点睛】明确半圆部分虚线左边比右边多的面积恰好就是阴影部分的面积是解决此题的关键。
13.4.275平方分米
【分析】根据题意可知,先设圆的半径为r,然后用r表示大正方形的面积,再根据大正方形的面积求出圆的面积,里面正方形的面积等于以圆的直径为底,圆的半径为直角边的四个三角形的面积之和,再根据阴影部分的面积=圆面积-小正方形面积得解。
【详解】设圆的半径为r
大正方形的面积=2r×2r=15
则r2=
圆的面积=πr2=3.14×=11.775(平方分米)
小正方形的面积=r×r÷2×4=7.5(平方分米)
阴影部分的面积=11.775-7.5=4.275(平方分米)
答:阴影部分的面积是4.275平方分米。
【点睛】解决本题的关键是将里面的正方形面积转化成两个三角形的面积,利用半径的平方,代入关系式再计算。
14.(1)222.8厘米
(2)486平方厘米
【分析】如下图所示:
(1)圆沿正方形边长内侧滚动一周的距离就是四个角上的圆弧长度与四条边上的线段之和。4个圆弧组成整圆,根据圆的周长=2πr求出整圆的周长,四条边上的线段都是正方形的边长减去圆的两个半径的长度,最后把两者加起来。
(2)圆滚不到的面积是四个角上的阴影部分面积和中间的小正方形的面积之和。四个阴影部分是用角上的小正方形的面积减去扇形的面积,根据正方形的面积=边长×边长、圆的面积=π解答。
【详解】(1)6分米=60厘米
3.14×10×2+(60-10-10)×4
=62.8+160
=222.8(厘米)
答:圆滚动的距离是222.8厘米。
(2)中间小正方形的边长:60-10×4
=60-40
=20(厘米)
(10×10-3.14××)×4+20×20
=(100-78.5)×4+400
=21.5×4+400
=86+400
=486(平方厘米)
答:这个圆滚不到部分的面积是486平方厘米。
【点睛】本题考查有关圆的组合图形的周长和面积运算,理解问题的具体所求是解题的关键。
15.12.78cm2
【分析】如下图所示,用③表示一块阴影部分的面积,则①-②=(①+③)-(②+③)。用半径是12cm的大扇形的面积减去半径是6cm的小扇形的面积即可得出①与③两阴影部分的面积之和,而②与③两阴影部分的面积之和等于长方形的面积,那么用大扇形的面积减去小扇形的面积,再减去长方形的面积,即可求出①与②两阴影部分的面积的差。图中扇形的面积是整圆面积的,根据S=πr2求出整圆面积,再除以4分别求出两个扇形的面积;根据长方形的面积=长×宽,求出长方形的面积。最后根据上面的分析结果进行解答。
【详解】
=3.14×27-72
(cm2)
答:①与②两阴影部分的面积的差是12.78cm2。
【点睛】把①与②两阴影部分的面积的差,转化为①与③的面积之和,与②与③面积之和的差,是解题的关键。再运用圆的面积公式和长方形的面积公式分别求出两部分的面积。
16.9.12平方米
【分析】如下图所示,分别连接点A、点B和半圆的交点,则两条虚线组成一个三角形,用半圆的面积减去三角形的面积,即求出阴影部分的面积。再乘4求出整个阴影部分的面积。根据圆的面积=π,三角形的面积=底×高÷2,即可解答。
【详解】半径:4÷2=2(米)
阴影部分的面积:3.14×÷2-4×2÷2
=3.14×4÷2-4
=6.28-4
=2.28(平方米)
整个阴影部分的面积:2.28×4=9.12(平方米)
【点睛】通过添加辅助线,用半圆的面积减去三角形的面积求出阴影部分的面积是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
