第三单元小数除法综合自检卷单元测试(含答案)数学五年级上册青岛版
文档属性
| 名称 | 第三单元小数除法综合自检卷单元测试(含答案)数学五年级上册青岛版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 10:24:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三单元小数除法综合自检卷(单元测试)数学五年级上册青岛版
一、选择题
1.因为23×65=1495,所以1.495÷0.23=( )。
A.0.65 B.6.5 C.65 D.0.065
2.商大于被除数的算式是( )。
A.7.2÷1.8 B.3.6÷1 C.9÷0.5 D.0.23÷3.6
3.已知甲数除以乙数的商是8.5,如果甲数扩大到原来的10倍,乙数缩小到原来的十分之一,则商是( )。
A.8.5 B.0.085 C.850 D.无法确定
4.手工小组的同学编织一个中国结需要3.5米红丝带,现有50米红丝带,最多可以编织( )个中国结。
A.13 B.14 C.15
5.一辆卡车的载重量是6吨,现有57吨货物运走,需要( )辆这样的卡车才能一次运完。
A.9 B.10 C.9.5 D.8
6.把一段木头锯成10段需要5.4分钟,锯成13段需要( )分钟。
A.7.02 B.5.4 C.7.8 D.7.2
二、填空题
7.妈妈用1.5元买了3千克白菜,每千克白菜( )元,1元能买( )千克白菜。
8.8.6÷0.07=( )÷7 38÷0.24=( )÷24
9.找规律填空。
(1)0.3,1.2,4.8,( ),( )。
(2)6.4,3.2,1.6,( ),( )。
10.在括号里填上“>”“<”或“=”。
( )5.6 ( )48.5 ( )
11.10.1÷3.3的商用循环小数记作( ),保留三位小数是( ),小数点后面第11位数字是( )。
12.甲数除以乙数的商是0.7,如果甲数不变,乙数扩大到原来的10倍,商是( )。
三、判断题
13.9.3333是循环小数。( )
14.用计算器计算8.045÷6时,漏掉了小数点,要纠正错误,应将结果除以1000。( )
15.0.98÷2.8,如果同时去掉被除数和除数的小数点,商不变。( )
16.0.25×0.04÷0.25×0.04的计算结果是1。( )
17.10千克油都放入瓶中,每瓶最多盛3千克,实际要准备3个这样的瓶子。( )
四、计算题
18.直接写得数。
7×0.9= 0.3×0.1= 4.2÷2.1= 4.5×2= 4÷0.8=
43.6+2.3= 3.2÷0.32= 8.8-7= 0.36÷0.09= 28÷4=
19.列竖式计算。(画△的得数保留两位小数)
△5.63÷7.8≈ 22.68÷2.7= 10.9×3.8=
20.脱式计算。(能简算的要简算)
五、解答题
21.8辆汽车5天节约汽油50.4升,照这样计算,25辆汽车7天节约汽油多少升?
22.国庆期间,明明一家自驾从德州到上海游玩,行驶了948千米,用了10.5小时,平均每小时行驶多少千米?(得数保留两位小数)
23.青岛和济南相距约351.6千米,一辆客车和一辆货车同时从两地相对开出,2小时后相遇。客车平均每小时行95千米,货车平均每小时行多少千米?
24.一间教室长9米,长是宽的1.5倍,用边长0.8米的地砖铺地,至少需要多少块?
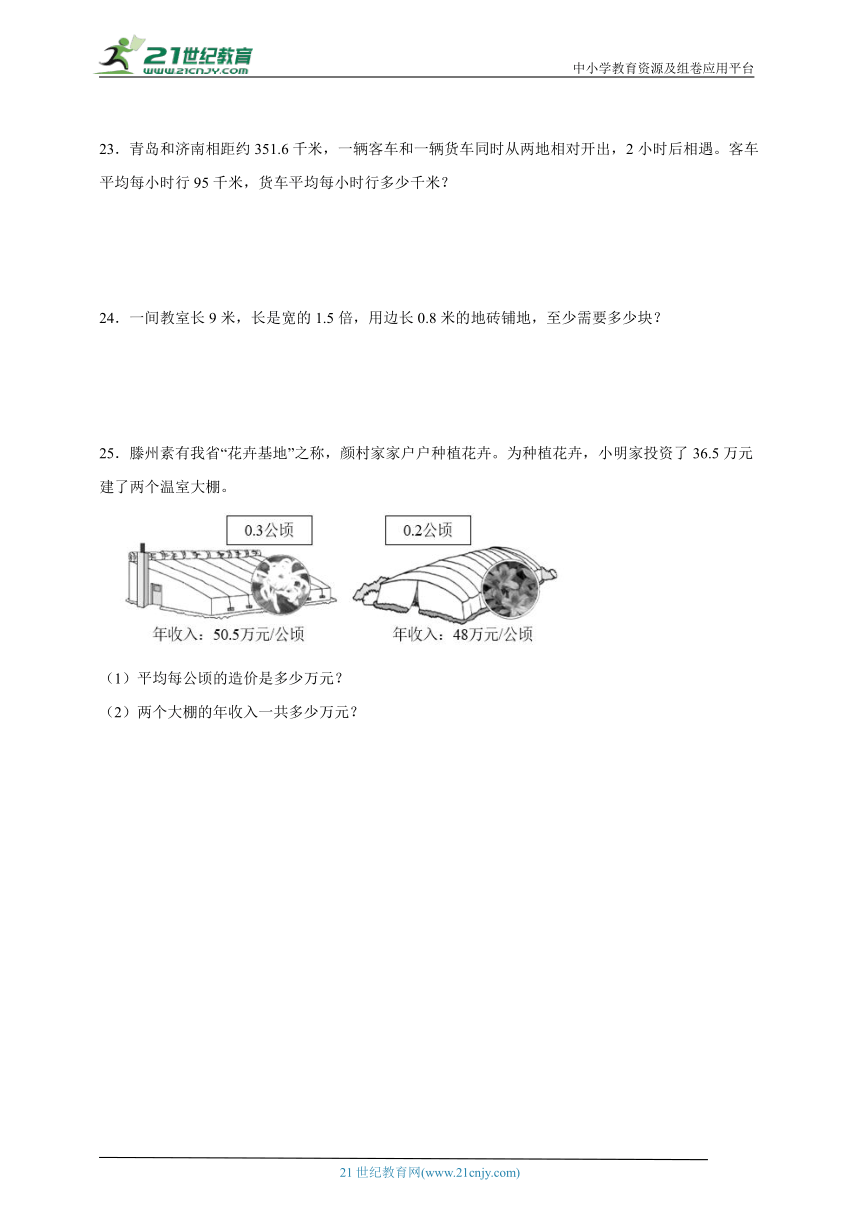
25.滕州素有我省“花卉基地”之称,颜村家家户户种植花卉。为种植花卉,小明家投资了36.5万元建了两个温室大棚。
(1)平均每公顷的造价是多少万元?
(2)两个大棚的年收入一共多少万元?
参考答案:
1.B
【分析】商的变化规律:除数不变,被除数乘几,商就乘几;被除数除以几,商就除以几;
被除数不变,除数乘几,商反而除以几;除数除以几,商反而乘几。
由23×65=1495可得出:1495÷23=65;
1.495÷0.23中,相当于被除数1495÷1000,除数23÷100,根据商的变化规律可知,商65÷1000×100,据此解答。
【详解】因为23×65=1495,则1495÷23=65;
65÷1000×100
=0.065×100
=6.5
所以1.495÷0.23=6.5。
故答案为:B
【点睛】本题考查商的变化规律的灵活运用。
2.C
【分析】一个数(0除外)除以大于1的数,商比原来的数小;
一个数(0除外)除以小于1的数,商比原来的数大;
一个数(0除外)除以1,商等于原来的数。
【详解】A.1.8>1,所以7.2÷1.8<7.2,商小于被除数,不符合题意;
B.3.6÷1=3.6,商等于被除数,不符合题意;
C.0.5<1,所以9÷0.5>9,商大于被除数,符合题意;
D.3.6>1,所以0.23÷3.6<0.23,商小于被除数,不符合题意。
故答案为:C
【点睛】掌握判断商与被除数之间大小关系的方法是解题的关键。
3.C
【分析】假设甲数是17,乙数是2,17÷2=8.5,它们的商是8.5,然后用甲数乘10,乙数除以10,再求出它们的商即可。
【详解】假设甲数是17,乙数是2
(17×10)÷(2÷10)
=170÷0.2
=850
则商是850。
故答案为:C
【点睛】本题考查小数除法,通过假设法可以使思路更清晰。
4.B
【分析】求50米红丝带最多可以编织几个中国结,也就是求50米里面有几个3.5米,用除法计算,得数采用“去尾法”取整数。
【详解】50÷3.5≈14(个)
最多可以编织14个中国结。
故答案为:B
【点睛】本题考查小数除法的应用以及商的近似数的求法,注意计算结果要结合生活实际,采用“去尾法”取近似数。
5.B
【分析】用需要运走的货物的质量除以6,即可求出需要多少辆这样的卡车才能一次运完。
【详解】57÷6≈10(辆)
所以,一辆卡车的载重量是6吨,现有57吨货物运走,需要10辆这样的卡车才能一次运完。
故答案为:B
【点睛】解答此题时,注意最后剩下的不够装满1车的货物,也需要1辆车,即用“进一法”求商的近似数。
6.D
【分析】把一段木头锯成10段,需要锯(10-1=9)次,由此可以求出锯1次需要的时间,锯成13段,需要锯(13-1=12)次,用锯的次数乘每锯一次需要的时间即可。
【详解】5.4÷(10-1)
=5.4÷9
=0.6(分钟)
0.6×(13-1)
=0.6×12
=7.2(分钟)
所以,把一段木头锯成10段需要5.4分钟,锯成13段需要7.2分钟。
故答案为:D
【点睛】本题考查了的锯木头问题,抓住锯的次数=锯出的段数-1,解题即可。
7. 0.5 2
【分析】已知用1.5元买了3千克白菜,根据“单价=总价÷数量”,即可求出每千克白菜的价钱;
求1元能买多少千克白菜,根据“数量=总价÷单价”,即可求解。
【详解】1.5÷3=0.5(元)
1÷0.5=2(千克)
每千克白菜0.5元,1元能买2千克白菜。
【点睛】本题考查小数除法的应用,掌握单价、数量、总价之间的关系是解题的关键。
8. 860 3800
【分析】除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0补足);然后按除数是整数的小数除法进行计算。
计算8.6÷0.07时,按照小数除法的计算法则,被除数、除数同时乘100,变成860÷7,商不变;
计算38÷0.24时,按照小数除法的计算法则,被除数、除数同时乘100,变成3800÷24,商不变。
【详解】8.6÷0.07=860÷7
38÷0.24=3800÷24
【点睛】本题考查除数是小数的除法计算法则,依据是商不变的规律。
9.(1) 19.2 76.8
(2) 0.8 0.4
【分析】(1)观察数列可知,前一个数乘4即可得到后一个数;
(2)观察数列可知,前一个数除以2即可得到后一个数。
【详解】(1)4.8×4=19.2
19.2×4=76.8
则0.3,1.2,4.8,19.2,76.8。
(2)1.6÷2=0.8
0.8÷2=0.4
则6.4,3.2,1.6,0.8,0.4。
【点睛】本题考查数字的排列规律,发现规律,利用规律是解题的关键。
10. > < =
【分析】根据积与因数的关系,一个数(0除外)乘一个大于1的数,所得的积比这个数大;根据商和被除数的关系,一个数(0除外)除以一个大于1的数,所得的商比被除数小;根据积不变的性质可知,两个因数相乘,一个因数扩大到原来的几倍,另一个因数缩小到原来的几分之一,积不变。据此判断。
【详解】1.4>1,所以>5.6
1.6>1,所以<48.5
=
【点睛】掌握积与因数的关系,商和被除数的关系,可以不用计算快速判断积与因数、商和被除数的大小。
11. 3.061 0
【分析】(1)一个无限小数,如果从小数部分的某一位起,都是由一个或几个数字依照一定的顺序连续不断地重复出现,这样的小数叫做“无限循环小数”,简称“循环小数”。重复出现的一个或几个数字,叫做“循环节”;简便写法:写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个圆点。
(2)按照“四舍五入”的原则,保留三位小数,即保留千分位上的数,而千分位后面的数,也即万分位上的数,如果大于或等于5时,那么就要向前进一位,如果小于5,就舍去。
(3)10.1÷3.3=3.060606…,3.060606…的循环节是06,用11除以循环节中数字的个数2,如果没有余数,小数点后面第11位数字就与循环节中的最后一个数字相同,如果有余数,余数是几,就与循环节中第几个数字相同。
【详解】10.1÷3.3
=3.060606…
=
10.1÷3.3≈3.061
11÷2=5……1
所以,10.1÷3.3的商用循环小数记作,保留三位小数是3.061,小数点后面第11位数字是0。
【点睛】本题考查了循环小数、循环节的意义,循环小数的简写方法,商的近似数,是基础知识,需要牢固掌握。
12.0.07
【分析】被除数不变,除数扩大几倍或缩小到原来的几分之一(0除外),商反而缩小到原来的几分之一或扩大相同的倍数。据此解答。
【详解】根据商的变化规律可知:
甲数除以乙数的商是0.7,如果甲数不变,乙数扩大到原来的10倍,商缩小到原来的;是0.7÷10=0.07
【点睛】此题考查了小数除法和商的变化规律的灵活运用。
13.×
【分析】从小数点后某一位开始不断地重复出现的一个或一节数字的无限小数,叫做循环小数。据此判断即可。
【详解】由分析可知:
9.3333是有限小数,不是循环小数。原题干说法错误。
故答案为:×
【点睛】本题考查循环小数,明确循环小数的定义是解题的关键。
14.√
【分析】用计算器计算8.045÷6时,漏掉了小数点,则被除数的小数点向右移动了三位,也就是扩大了1000倍;
在商不为0的除法算式里,除数不变,被除数扩大1000倍,则商也会扩大1000倍,依此判断即可。
【详解】8.045×1000=8045
用计算器计算8.045÷6时,漏掉了小数点,要纠正错误,应将结果除以1000。
故答案为:√
【点睛】此题考查的是商的变化规律,应熟练掌握小数点位置的移动方法。
15.×
【分析】由题意可知,在算式0.98÷2.8中,如果把被除数除数的小数点同时去掉,则被除数扩大到原来的100倍,除数扩大到原来的10倍,根据商的变化规律,则商乘100÷10=10。据此判断即可。
【详解】在0.98÷2.8中,如果同时去掉被除数和除数的小数点,变为98÷28,
相当于被除数扩大到原来的100倍,除数扩大到原来的10倍,那么商会扩大到原来的10倍。
故答案为:×
【点睛】本题考查小数除法,掌握商的变化规律是解题的关键。
16.×
【分析】按照乘除混合运算顺序,从左到右进行计算即可。
【详解】0.25×0.04÷0.25×0.04
=0.01÷0.25×0.04
=0.04×0.04
=0.0016
0.0016<1
原题说法错误。
故答案为:×
【点睛】本题考查小数乘除法,明确乘除混合运算顺序是解题的关键。
17.×
【分析】用10千克除以3千克,利用进一法将商保留到整数部分,求出需要准备的瓶子数量。
【详解】10÷3≈4(个),所以,实际要准备4个这样的瓶子。
所以判断错误。
故答案为:×
【点睛】本题考查了商的近似数,能根据实际情况采用进一法求近似数是解题的关键。
18.6.3;0.03;2;9;5;
45.9;10;1.8;4;7
【详解】略
19.0.72;8.4;41.42
【分析】计算小数乘法时,先按照整数乘法计算出积,再点小数点,看因数中一共有几位小数就从积的右边起数出几位点上小数点,位数不够时用0补足,小数部分末尾的0要去掉;
计算除数是小数的小数除法时,先移动除数的小数点使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾用0补足),然后按照除数是整数的小数除法进行计算,商保留两位小数时,要除到小数点后面第三位,再根据四舍五入取近似值,据此解答。
【详解】△5.63÷7.8≈0.72 22.68÷2.7=8.4 10.9×3.8=41.42
20.0.78;11
36.36;1.7
【分析】(1)根据乘法交换律a×b=b×a进行简算;
(2)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(3)先把10.1分解成10+0.1,然后根据乘法分配律(a+b)×c=a×c+b×c进行简算;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算中括号外面的除法。
【详解】(1)
(2)
(3)
(4)
21.220.5升
【分析】根据除法的意义,用50.4除以8再除以5即可得到1辆汽车1天可节约的汽油,再乘25,再乘7即可求出25辆汽车7天节约汽油多少升。
【详解】50.4÷8÷5×25×7
=6.3÷5×25×7
=1.26×25×7
=31.5×7
=220.5(升)
答:25辆汽车7天节约汽油220.5升。
【点睛】本题考查小数乘除法,求出1辆汽车1天可节约的汽油的升数是解题的关键。
22.90.29千米
【分析】根据路程÷时间=速度,即用948除以10.5,然后运用“四舍五入”法保留两位小数即可。
【详解】(千米)
答:平均每小时行驶90.29千米。
【点睛】本题考查小数除法,明确路程、时间和速度之间的关系是解题的关键。
23.80.8千米
【分析】根据相遇问题中,速度和×相遇时间=相遇路程,即用351.6除以2即可得到客车和货车的速度和,用它们的速度和减去客车的速度即可求出货车的速度。
【详解】
(千米)
答:货车平均每小时行80.8千米。
【点睛】本题考查小数除法,求出客车和货车的速度和是解题的关键。
24.85块
【分析】根据已知一个数的几倍是多少,求这个数,用除法计算,用9除以1.5即可求出教室的宽,再根据长方形的面积公式:S=ab,据此求出教室的面积,根据正方形的面积公式:S=a2,据此求出地砖的面积,然后用教室的面积除以地砖的面积,其结果根据实际情况运用“进一法”保留整数即可。
【详解】9×(9÷1.5)÷(0.8×0.8)
=9×6÷0.64
=54÷0.64
=84.375
≈85(块)
答:至少需要85块。
【点睛】本题考查小数乘除法,结合长方形和正方形的面积的计算方法是解题的关键。
25.(1)73万元;
(2)24.75万元
【分析】(1)两个温室大棚的面积等于(0.3+0.2)公顷,投资36.5万元,根据平均数的意义,用36.5除以(0.3+0.2),即可求出平均每公顷的造价是多少万元。
(2)用第一个温室大棚每公顷的年收入乘第一个温室大棚的面积,求出第一个温室大棚的年收入,用第二个温室大棚每公顷的年收入乘第二个温室大棚的面积,求出第二个温室大棚的年收入,把两个大棚的年收入加起来,即可得解。
【详解】(1)36.5÷(0.3+0.2)
=36.5÷0.5
=73(万元)
答:平均每公顷的造价是73万元。
(2)50.5×0.3+48×0.2
=15.15+9.6
=24.75(万元)
答:两个大棚的年收入一共24.75万元。
【点睛】此题主要考查小数乘除法在实际生活中的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三单元小数除法综合自检卷(单元测试)数学五年级上册青岛版
一、选择题
1.因为23×65=1495,所以1.495÷0.23=( )。
A.0.65 B.6.5 C.65 D.0.065
2.商大于被除数的算式是( )。
A.7.2÷1.8 B.3.6÷1 C.9÷0.5 D.0.23÷3.6
3.已知甲数除以乙数的商是8.5,如果甲数扩大到原来的10倍,乙数缩小到原来的十分之一,则商是( )。
A.8.5 B.0.085 C.850 D.无法确定
4.手工小组的同学编织一个中国结需要3.5米红丝带,现有50米红丝带,最多可以编织( )个中国结。
A.13 B.14 C.15
5.一辆卡车的载重量是6吨,现有57吨货物运走,需要( )辆这样的卡车才能一次运完。
A.9 B.10 C.9.5 D.8
6.把一段木头锯成10段需要5.4分钟,锯成13段需要( )分钟。
A.7.02 B.5.4 C.7.8 D.7.2
二、填空题
7.妈妈用1.5元买了3千克白菜,每千克白菜( )元,1元能买( )千克白菜。
8.8.6÷0.07=( )÷7 38÷0.24=( )÷24
9.找规律填空。
(1)0.3,1.2,4.8,( ),( )。
(2)6.4,3.2,1.6,( ),( )。
10.在括号里填上“>”“<”或“=”。
( )5.6 ( )48.5 ( )
11.10.1÷3.3的商用循环小数记作( ),保留三位小数是( ),小数点后面第11位数字是( )。
12.甲数除以乙数的商是0.7,如果甲数不变,乙数扩大到原来的10倍,商是( )。
三、判断题
13.9.3333是循环小数。( )
14.用计算器计算8.045÷6时,漏掉了小数点,要纠正错误,应将结果除以1000。( )
15.0.98÷2.8,如果同时去掉被除数和除数的小数点,商不变。( )
16.0.25×0.04÷0.25×0.04的计算结果是1。( )
17.10千克油都放入瓶中,每瓶最多盛3千克,实际要准备3个这样的瓶子。( )
四、计算题
18.直接写得数。
7×0.9= 0.3×0.1= 4.2÷2.1= 4.5×2= 4÷0.8=
43.6+2.3= 3.2÷0.32= 8.8-7= 0.36÷0.09= 28÷4=
19.列竖式计算。(画△的得数保留两位小数)
△5.63÷7.8≈ 22.68÷2.7= 10.9×3.8=
20.脱式计算。(能简算的要简算)
五、解答题
21.8辆汽车5天节约汽油50.4升,照这样计算,25辆汽车7天节约汽油多少升?
22.国庆期间,明明一家自驾从德州到上海游玩,行驶了948千米,用了10.5小时,平均每小时行驶多少千米?(得数保留两位小数)
23.青岛和济南相距约351.6千米,一辆客车和一辆货车同时从两地相对开出,2小时后相遇。客车平均每小时行95千米,货车平均每小时行多少千米?
24.一间教室长9米,长是宽的1.5倍,用边长0.8米的地砖铺地,至少需要多少块?
25.滕州素有我省“花卉基地”之称,颜村家家户户种植花卉。为种植花卉,小明家投资了36.5万元建了两个温室大棚。
(1)平均每公顷的造价是多少万元?
(2)两个大棚的年收入一共多少万元?
参考答案:
1.B
【分析】商的变化规律:除数不变,被除数乘几,商就乘几;被除数除以几,商就除以几;
被除数不变,除数乘几,商反而除以几;除数除以几,商反而乘几。
由23×65=1495可得出:1495÷23=65;
1.495÷0.23中,相当于被除数1495÷1000,除数23÷100,根据商的变化规律可知,商65÷1000×100,据此解答。
【详解】因为23×65=1495,则1495÷23=65;
65÷1000×100
=0.065×100
=6.5
所以1.495÷0.23=6.5。
故答案为:B
【点睛】本题考查商的变化规律的灵活运用。
2.C
【分析】一个数(0除外)除以大于1的数,商比原来的数小;
一个数(0除外)除以小于1的数,商比原来的数大;
一个数(0除外)除以1,商等于原来的数。
【详解】A.1.8>1,所以7.2÷1.8<7.2,商小于被除数,不符合题意;
B.3.6÷1=3.6,商等于被除数,不符合题意;
C.0.5<1,所以9÷0.5>9,商大于被除数,符合题意;
D.3.6>1,所以0.23÷3.6<0.23,商小于被除数,不符合题意。
故答案为:C
【点睛】掌握判断商与被除数之间大小关系的方法是解题的关键。
3.C
【分析】假设甲数是17,乙数是2,17÷2=8.5,它们的商是8.5,然后用甲数乘10,乙数除以10,再求出它们的商即可。
【详解】假设甲数是17,乙数是2
(17×10)÷(2÷10)
=170÷0.2
=850
则商是850。
故答案为:C
【点睛】本题考查小数除法,通过假设法可以使思路更清晰。
4.B
【分析】求50米红丝带最多可以编织几个中国结,也就是求50米里面有几个3.5米,用除法计算,得数采用“去尾法”取整数。
【详解】50÷3.5≈14(个)
最多可以编织14个中国结。
故答案为:B
【点睛】本题考查小数除法的应用以及商的近似数的求法,注意计算结果要结合生活实际,采用“去尾法”取近似数。
5.B
【分析】用需要运走的货物的质量除以6,即可求出需要多少辆这样的卡车才能一次运完。
【详解】57÷6≈10(辆)
所以,一辆卡车的载重量是6吨,现有57吨货物运走,需要10辆这样的卡车才能一次运完。
故答案为:B
【点睛】解答此题时,注意最后剩下的不够装满1车的货物,也需要1辆车,即用“进一法”求商的近似数。
6.D
【分析】把一段木头锯成10段,需要锯(10-1=9)次,由此可以求出锯1次需要的时间,锯成13段,需要锯(13-1=12)次,用锯的次数乘每锯一次需要的时间即可。
【详解】5.4÷(10-1)
=5.4÷9
=0.6(分钟)
0.6×(13-1)
=0.6×12
=7.2(分钟)
所以,把一段木头锯成10段需要5.4分钟,锯成13段需要7.2分钟。
故答案为:D
【点睛】本题考查了的锯木头问题,抓住锯的次数=锯出的段数-1,解题即可。
7. 0.5 2
【分析】已知用1.5元买了3千克白菜,根据“单价=总价÷数量”,即可求出每千克白菜的价钱;
求1元能买多少千克白菜,根据“数量=总价÷单价”,即可求解。
【详解】1.5÷3=0.5(元)
1÷0.5=2(千克)
每千克白菜0.5元,1元能买2千克白菜。
【点睛】本题考查小数除法的应用,掌握单价、数量、总价之间的关系是解题的关键。
8. 860 3800
【分析】除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0补足);然后按除数是整数的小数除法进行计算。
计算8.6÷0.07时,按照小数除法的计算法则,被除数、除数同时乘100,变成860÷7,商不变;
计算38÷0.24时,按照小数除法的计算法则,被除数、除数同时乘100,变成3800÷24,商不变。
【详解】8.6÷0.07=860÷7
38÷0.24=3800÷24
【点睛】本题考查除数是小数的除法计算法则,依据是商不变的规律。
9.(1) 19.2 76.8
(2) 0.8 0.4
【分析】(1)观察数列可知,前一个数乘4即可得到后一个数;
(2)观察数列可知,前一个数除以2即可得到后一个数。
【详解】(1)4.8×4=19.2
19.2×4=76.8
则0.3,1.2,4.8,19.2,76.8。
(2)1.6÷2=0.8
0.8÷2=0.4
则6.4,3.2,1.6,0.8,0.4。
【点睛】本题考查数字的排列规律,发现规律,利用规律是解题的关键。
10. > < =
【分析】根据积与因数的关系,一个数(0除外)乘一个大于1的数,所得的积比这个数大;根据商和被除数的关系,一个数(0除外)除以一个大于1的数,所得的商比被除数小;根据积不变的性质可知,两个因数相乘,一个因数扩大到原来的几倍,另一个因数缩小到原来的几分之一,积不变。据此判断。
【详解】1.4>1,所以>5.6
1.6>1,所以<48.5
=
【点睛】掌握积与因数的关系,商和被除数的关系,可以不用计算快速判断积与因数、商和被除数的大小。
11. 3.061 0
【分析】(1)一个无限小数,如果从小数部分的某一位起,都是由一个或几个数字依照一定的顺序连续不断地重复出现,这样的小数叫做“无限循环小数”,简称“循环小数”。重复出现的一个或几个数字,叫做“循环节”;简便写法:写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个圆点。
(2)按照“四舍五入”的原则,保留三位小数,即保留千分位上的数,而千分位后面的数,也即万分位上的数,如果大于或等于5时,那么就要向前进一位,如果小于5,就舍去。
(3)10.1÷3.3=3.060606…,3.060606…的循环节是06,用11除以循环节中数字的个数2,如果没有余数,小数点后面第11位数字就与循环节中的最后一个数字相同,如果有余数,余数是几,就与循环节中第几个数字相同。
【详解】10.1÷3.3
=3.060606…
=
10.1÷3.3≈3.061
11÷2=5……1
所以,10.1÷3.3的商用循环小数记作,保留三位小数是3.061,小数点后面第11位数字是0。
【点睛】本题考查了循环小数、循环节的意义,循环小数的简写方法,商的近似数,是基础知识,需要牢固掌握。
12.0.07
【分析】被除数不变,除数扩大几倍或缩小到原来的几分之一(0除外),商反而缩小到原来的几分之一或扩大相同的倍数。据此解答。
【详解】根据商的变化规律可知:
甲数除以乙数的商是0.7,如果甲数不变,乙数扩大到原来的10倍,商缩小到原来的;是0.7÷10=0.07
【点睛】此题考查了小数除法和商的变化规律的灵活运用。
13.×
【分析】从小数点后某一位开始不断地重复出现的一个或一节数字的无限小数,叫做循环小数。据此判断即可。
【详解】由分析可知:
9.3333是有限小数,不是循环小数。原题干说法错误。
故答案为:×
【点睛】本题考查循环小数,明确循环小数的定义是解题的关键。
14.√
【分析】用计算器计算8.045÷6时,漏掉了小数点,则被除数的小数点向右移动了三位,也就是扩大了1000倍;
在商不为0的除法算式里,除数不变,被除数扩大1000倍,则商也会扩大1000倍,依此判断即可。
【详解】8.045×1000=8045
用计算器计算8.045÷6时,漏掉了小数点,要纠正错误,应将结果除以1000。
故答案为:√
【点睛】此题考查的是商的变化规律,应熟练掌握小数点位置的移动方法。
15.×
【分析】由题意可知,在算式0.98÷2.8中,如果把被除数除数的小数点同时去掉,则被除数扩大到原来的100倍,除数扩大到原来的10倍,根据商的变化规律,则商乘100÷10=10。据此判断即可。
【详解】在0.98÷2.8中,如果同时去掉被除数和除数的小数点,变为98÷28,
相当于被除数扩大到原来的100倍,除数扩大到原来的10倍,那么商会扩大到原来的10倍。
故答案为:×
【点睛】本题考查小数除法,掌握商的变化规律是解题的关键。
16.×
【分析】按照乘除混合运算顺序,从左到右进行计算即可。
【详解】0.25×0.04÷0.25×0.04
=0.01÷0.25×0.04
=0.04×0.04
=0.0016
0.0016<1
原题说法错误。
故答案为:×
【点睛】本题考查小数乘除法,明确乘除混合运算顺序是解题的关键。
17.×
【分析】用10千克除以3千克,利用进一法将商保留到整数部分,求出需要准备的瓶子数量。
【详解】10÷3≈4(个),所以,实际要准备4个这样的瓶子。
所以判断错误。
故答案为:×
【点睛】本题考查了商的近似数,能根据实际情况采用进一法求近似数是解题的关键。
18.6.3;0.03;2;9;5;
45.9;10;1.8;4;7
【详解】略
19.0.72;8.4;41.42
【分析】计算小数乘法时,先按照整数乘法计算出积,再点小数点,看因数中一共有几位小数就从积的右边起数出几位点上小数点,位数不够时用0补足,小数部分末尾的0要去掉;
计算除数是小数的小数除法时,先移动除数的小数点使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾用0补足),然后按照除数是整数的小数除法进行计算,商保留两位小数时,要除到小数点后面第三位,再根据四舍五入取近似值,据此解答。
【详解】△5.63÷7.8≈0.72 22.68÷2.7=8.4 10.9×3.8=41.42
20.0.78;11
36.36;1.7
【分析】(1)根据乘法交换律a×b=b×a进行简算;
(2)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(3)先把10.1分解成10+0.1,然后根据乘法分配律(a+b)×c=a×c+b×c进行简算;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算中括号外面的除法。
【详解】(1)
(2)
(3)
(4)
21.220.5升
【分析】根据除法的意义,用50.4除以8再除以5即可得到1辆汽车1天可节约的汽油,再乘25,再乘7即可求出25辆汽车7天节约汽油多少升。
【详解】50.4÷8÷5×25×7
=6.3÷5×25×7
=1.26×25×7
=31.5×7
=220.5(升)
答:25辆汽车7天节约汽油220.5升。
【点睛】本题考查小数乘除法,求出1辆汽车1天可节约的汽油的升数是解题的关键。
22.90.29千米
【分析】根据路程÷时间=速度,即用948除以10.5,然后运用“四舍五入”法保留两位小数即可。
【详解】(千米)
答:平均每小时行驶90.29千米。
【点睛】本题考查小数除法,明确路程、时间和速度之间的关系是解题的关键。
23.80.8千米
【分析】根据相遇问题中,速度和×相遇时间=相遇路程,即用351.6除以2即可得到客车和货车的速度和,用它们的速度和减去客车的速度即可求出货车的速度。
【详解】
(千米)
答:货车平均每小时行80.8千米。
【点睛】本题考查小数除法,求出客车和货车的速度和是解题的关键。
24.85块
【分析】根据已知一个数的几倍是多少,求这个数,用除法计算,用9除以1.5即可求出教室的宽,再根据长方形的面积公式:S=ab,据此求出教室的面积,根据正方形的面积公式:S=a2,据此求出地砖的面积,然后用教室的面积除以地砖的面积,其结果根据实际情况运用“进一法”保留整数即可。
【详解】9×(9÷1.5)÷(0.8×0.8)
=9×6÷0.64
=54÷0.64
=84.375
≈85(块)
答:至少需要85块。
【点睛】本题考查小数乘除法,结合长方形和正方形的面积的计算方法是解题的关键。
25.(1)73万元;
(2)24.75万元
【分析】(1)两个温室大棚的面积等于(0.3+0.2)公顷,投资36.5万元,根据平均数的意义,用36.5除以(0.3+0.2),即可求出平均每公顷的造价是多少万元。
(2)用第一个温室大棚每公顷的年收入乘第一个温室大棚的面积,求出第一个温室大棚的年收入,用第二个温室大棚每公顷的年收入乘第二个温室大棚的面积,求出第二个温室大棚的年收入,把两个大棚的年收入加起来,即可得解。
【详解】(1)36.5÷(0.3+0.2)
=36.5÷0.5
=73(万元)
答:平均每公顷的造价是73万元。
(2)50.5×0.3+48×0.2
=15.15+9.6
=24.75(万元)
答:两个大棚的年收入一共24.75万元。
【点睛】此题主要考查小数乘除法在实际生活中的应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
