第12章全等三角形 解答题优生辅导专题训练 2023-2024学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 第12章全等三角形 解答题优生辅导专题训练 2023-2024学年人教版八年级数学上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 591.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
2023-2024学年人教版八年级数学上册《第12章全等三角形》
解答题优生辅导专题训练(附答案)
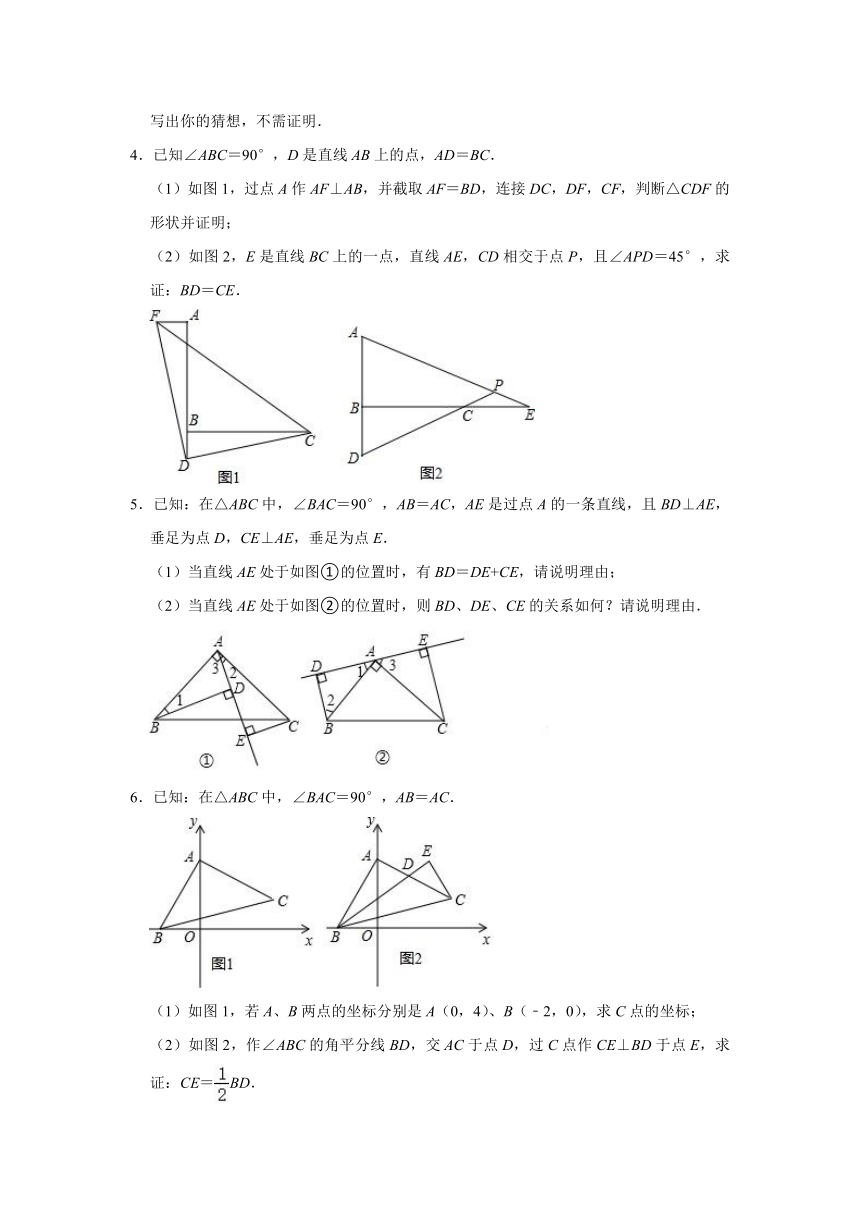
1.如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH;
(2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
2.如图1,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,连接ED交BC于F,DF=EF.
(1)求证:BD=CE;
(2)如图2,连接CD,若∠DFB=45°,BC=6,求△BCD的面积.
3.已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD、DC(或它们的延长线)于E、F.
(1)当∠MBN绕B点旋转到AE=CF时(如图1),求证:AE+CF=EF;
(2)当∠MBN绕B点旋转到AE≠CF时,在 图2和 图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明.
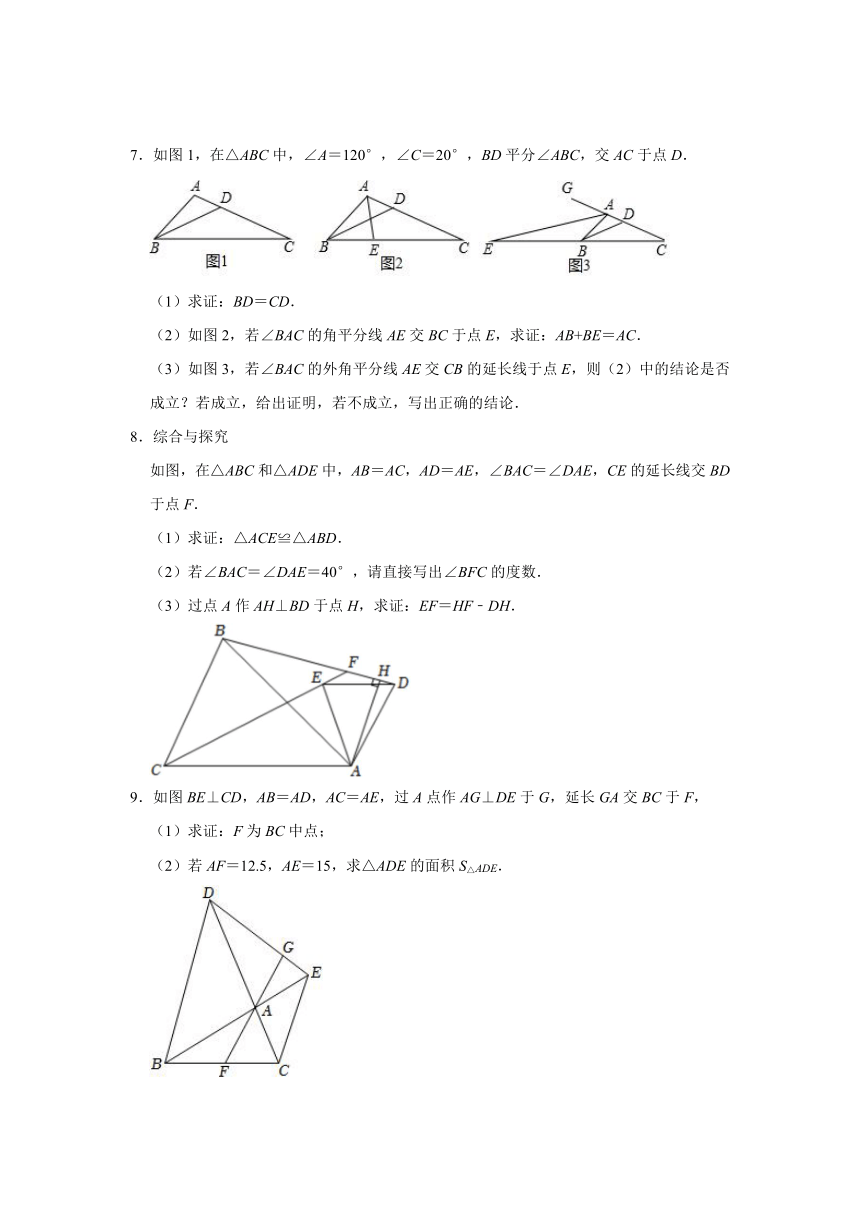
4.已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
5.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE,垂足为点D,CE⊥AE,垂足为点E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由.
6.已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若A、B两点的坐标分别是A(0,4)、B(﹣2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE=BD.
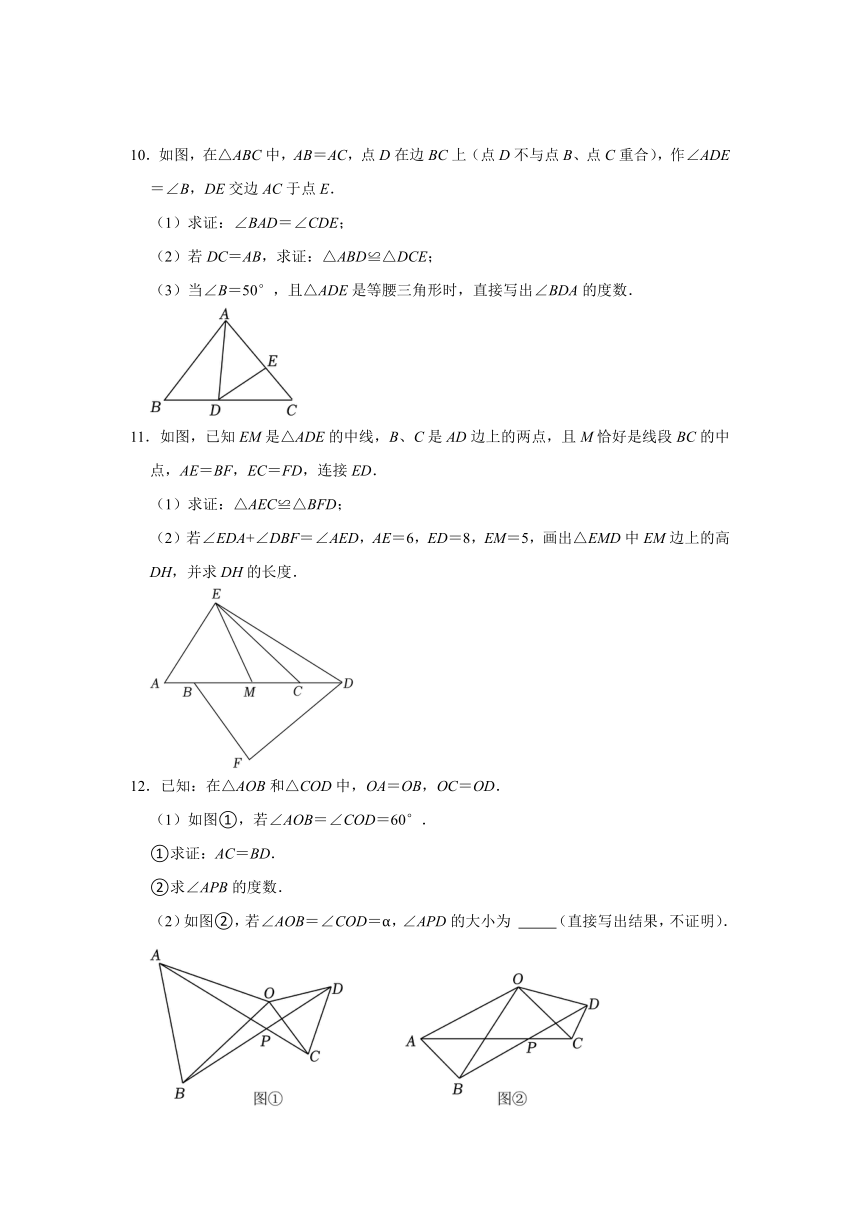
7.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.
(1)求证:BD=CD.
(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.
(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.
8.综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=40°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF=HF﹣DH.
9.如图BE⊥CD,AB=AD,AC=AE,过A点作AG⊥DE于G,延长GA交BC于F,
(1)求证:F为BC中点;
(2)若AF=12.5,AE=15,求△ADE的面积S△ADE.
10.如图,在△ABC中,AB=AC,点D在边BC上(点D不与点B、点C重合),作∠ADE
=∠B,DE交边AC于点E.
(1)求证:∠BAD=∠CDE;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)当∠B=50°,且△ADE是等腰三角形时,直接写出∠BDA的度数.
11.如图,已知EM是△ADE的中线,B、C是AD边上的两点,且M恰好是线段BC的中点,AE=BF,EC=FD,连接ED.
(1)求证:△AEC≌△BFD;
(2)若∠EDA+∠DBF=∠AED,AE=6,ED=8,EM=5,画出△EMD中EM边上的高DH,并求DH的长度.
12.已知:在△AOB和△COD中,OA=OB,OC=OD.
(1)如图①,若∠AOB=∠COD=60°.
①求证:AC=BD.
②求∠APB的度数.
(2)如图②,若∠AOB=∠COD=α,∠APD的大小为 (直接写出结果,不证明).
13.如图,在△ABC中,AB<BC,过点A作线段AD∥BC,连接BD,且满足AD+BD=BC.取AC的中点E,连接BE、DE.
(1)若AB=4、BC=6,直接写出BE的取值范围 ;
(2)求证:BE⊥DE.
14.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.(1)求证:EF=BE+FD;
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?
15.如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:
①△BPD≌△CQP;
②∠DPQ=∠B;
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ为等腰三角形?
16.如图,在Rt△ABC中,∠ABC=90°,在Rt△EBD中,∠EBD=90°,AB=EB,∠BCA=∠BDE
(1)求证:CA=DE;
(2)连接EC,连接AD,交BC于F,若F恰好是AD的中点,求证:BF=EC.
17.AB=AC,BD=CD,EG⊥AB,GF⊥AC.
(1)若∠BAC=90°,求证ED=FD;
(2)若∠BAC≠90°,则(1)的结论是否成立?
18.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点(不与A、B重合).
(1)求证:△ACE≌△BCD;
(2)若AD=2,BD=4,求ED的长.
19.在平面直角坐标系中,三角形ABC为等腰直角三角形,AC=BC,BC交x轴于点D.
(1)若A(﹣8,0),C(0,6),直接写出点B的坐标 ;
(2)如图2,△OAB与△ACD均为等腰直角三角形,连OD,求∠AOD的度数;
(3)如图3,若AD平分∠BAC,A(﹣8,0),D(m,0),B的纵坐标为n,求2n+m的值.
20.如图,△ABC中,∠ABC=∠ACB,点D、E、F分别是AB、BC、AC边上的点,BE=CF.
(1)若∠DEF=∠ABC,求证:DE=EF;
(2)若∠A+2∠DEF=180°,BC=9,EC=2BE,求BD的长;
(3)把(1)中的条件和结论反过来,即:若DE=EF,则∠DEF=∠ABC;这个命题是否成立?若成立,请证明;若不成立,请说明理由.
参考答案
1.(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵∠ABC=∠GBH,
∴∠A=∠GBH.
∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.
在△ADG和△CDF中,
,
∴△AEF≌△BGH(AAS).
(2)解:∵△AEF≌△BGH,
∴AF=BH,
∴AB=FH=4.
∵EF⊥AB,GH⊥AB,
∴∠EFD=∠GHD.
在△EFD和△GHD中,
∴△EFD≌△GHD(AAS),
∴.
2.(1)证明:如图1,过点D作DG∥AE,交BC于点G,
∴∠FDG=∠E,
在△DGF和△ECF中,
,
∴△DGF≌△ECF(ASA),
∴DG=CE,
∵AB=AC,
∴∠B=∠ACB,
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠DBG=∠DGB,
∴DG=BD,
∴BD=CE;
(2)解:如图2,过点D作DG∥AE,交BC于点G,过点D作DH⊥BC于点H,
∵DB=DG,
∴BH=GH,
由(1)知△DGF≌△ECF,
∴GF=CF,
∴HF=BC=3,
∵DH⊥BC,∠DFB=45°,
∴△DHF是等腰直角三角形,
∴DH=HF=3,
∴S△CDB=BC DH=6×3=9.
3.解:(1)如图1中,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS).
∴BE=BF,∴∠ABE=∠CBF=(∠ABC﹣∠MBN)=(120°﹣60°)=30°.
∴AE=BE,CF=BF,
△BEF是等边三角形.
∴BE=BF=EF.
∴AE+CF=BE+BF=EF;
(2)①如图2中,结论仍然成立.理由如下:
延长DC至K点使得CK=AE,
在△ABE和△CBK中,
,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°,
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
,
∴△EBF≌△KBF(SAS).
∴EF=KF.
∴EF=CK+CF.
∴AE+CF=EF;
③如图3,结论不成立.猜想AE﹣CF=EF,理由如下:
证明如下:在DC的延长线上取点K,使CK=AE,连接BK.
在△ABE和△CBK中,
,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°.
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
,
∴△EBF≌△KBF(SAS),
∴EF=KF,
∴EF=CK﹣CF.
∴AE﹣CF=EF.
4.解:(1)∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
,
∴△FAD≌△DBC(SAS);
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形.
(2)如图2,作AF⊥AB于A,使AF=BD,连接DF,CF,
∴∠FAD=90°.
∵∠ABC=90°,
∴∠FAD=∠DBC=90°.
在△FAD和△DBC中,
,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°.
∵∠APD=45°,
∴∠FCD=∠APD,
∴CF∥AE.
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,
∴CE=BD.
5.证明:(1)∵∠BAC=90°,
∴∠2+∠3=90°,
∵BD⊥AE,
∴∠1+∠3=90°,
∴∠1=∠2,
在△ABD和△CAE中,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE﹣CE,
理由如下:∵∠BAC=90°,
∴∠1+∠3=90°,
∵BD⊥AE,
∴∠1+∠2=90°,
∴∠2=∠3,
在△ABD和△CAE中,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AE=DE﹣AD,
∴BD=DE﹣CE.
6.解:(1)如图1中,作CM⊥OA垂足为M,则∠AMC=90°,
∵∠BAC=∠AOB=90°,
∴∠BAO+∠CAM=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠CAM,
在△ABO和△CAM中,
,
∴△ABO≌△CAM(AAS),
∴MC=AO,AM=BO,
∵A(0,4)、B(﹣2,0),
∴AO=4,BO=2,
∴MC=4,AM=2,MO=AO﹣AM=2,
∴点C坐标(4,2);
(2)如图2,延长CE、BA相交于点F,
∵BE⊥CE,∠BAC=90°,
∴∠EBF+∠F=90°,∠ACF+∠F=90°,
∴∠EBF=∠ACF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵BE⊥CF,BE平分∠FBC,
∴△BCF是等腰三角形,CF是底边,
∴CE=,
∴CE=BD.
7.(1)证明:∵∠A=120°,∠C=20°,
∴∠ABC=180°﹣120°﹣20°=40°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=ABC=20°,
∴∠DBC=∠C=20°,
∴BD=CD;
(2)证明:如图2,过点E作EF∥BD交AC于点F,
∴∠FEC=∠DBC=20°,
∴∠FEC=∠C=20°,
∴∠AFE=40°,FE=FC,
∴∠AFE=∠ABC,
∵AE是∠BAC的平分线,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS),
∴BE=EF,
∴BE=EF=FC,
∴AB+BE=AF+FC=AC;
(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:
如图3,过点A作AF∥BD交BE于点F,
∴∠AFC=∠DBC=20°,
∴∠AFC=∠C=20°,
∴AF=AC,
∵AE是∠BAC的外角平分线,
∴∠EAB=(180°﹣∠ABC)=30°,
∵∠ABC=40°,
∴∠E=∠ABC﹣∠EAB=10°,
∴∠E=∠FAE=10°,
∴FE=AF,
∴FE=AF=AC,
∴BE﹣AB=BE﹣BF=EF=AC.
8.(1)证明:∵∠BAC=∠DAE.
∴∠CAE=∠BAD.
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴∠AEC=∠ADB,
∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,
∵∠BFC+∠DFE=180°,
∴∠BFC=∠DAE=∠BAC=40°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.
∵△ACE≌△ABD,
∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD,
∴CE AJ=BD AH,
∴AJ=AH,
在Rt△AFJ和Rt△AFH中,
,
∴Rt△AFJ≌Rt△AFH(HL),
∴FJ=FH,
在Rt△AJE和Rt△AHD中,
,
∴Rt△AJE≌Rt△AHD(HL),
∴EJ=DH,
∴EF=FJ﹣EJ=FH﹣DH.
∴EF=HF﹣DH.
9.(1)证明:∵BE⊥CD,
∴∠DAE=∠DAB=∠BAC=∠CAE=90°,
在△ADE和△ABC中,
,
∴△ADE≌△ABC (SAS),
∴∠DEA=∠BCA,
∵AG⊥DE,
∴∠AGD=90°,
∴∠AED+∠ADE=∠DAG+∠ADE=90°,
∴∠AED=∠DAG,
∵∠DAG=∠CAF,
∴∠CAF=∠FCA,
∴FC=FA,
∵∠BAC=90°,
∴∠FAC+∠BAF=∠FCA+∠FBA=90°,
∴∠BAF=∠FBA,
∴FB=FA,
∴FB=FC,
∴F是BC的中点;
(2)解:∵F为BC的中点,∠BAC=90°,
∴AF=BC,
∴BC=2AF=25,
由△ABC≌△ADE知:DE=BC=25,
∵AE=15,∠DAE=90°,
∴AD=20,
∴S△ADE=AD AE=20×15=150.
10.(1)证明:∠ADE=∠B,∠BAD+∠B=∠ADC,∠CDE+∠ADE=∠ADC,
∴∠BAD=∠CDE;
(2)证明:∵AB=AC,
∴∠B=∠C,
∵DC=AB,∠BAD=∠CDE;
在△ABD和△DCE中,
,
∴△ABD≌△DCE(SAS);
(3)解:∵∠B=∠C=50°,∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣50°=80°,
分三种情况讨论:
①当DA=DE时,∠DAE=∠DEA,
∵∠ADE=∠B=50°,∠ADE+∠DAE+∠DEA=180°,
∴∠DAE=(180°﹣50°)÷2=65°,
∴∠BAD=∠BAC﹣∠DAE=80°﹣65°=15°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°﹣∠B﹣∠BAD=180°﹣50°﹣15°=115°;
②当AD=AE时,∠AED=∠ADE=50°,
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°﹣∠AED﹣∠ADE=180°﹣50°﹣50°=80°,
∵∠BAC=80°,
∴∠DAE=∠BAE,
∴点D与点B重合,不合题意.
③当EA=ED时,∠DAE=∠ADE=50°,
∴∠BAD=∠BAC﹣∠DAE=80°﹣50°=30°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°﹣∠B﹣∠BAD=180°﹣50°﹣30°=100°,
综上所述,当∠BDA的度数为115°或100°时,△ADE是等腰三角形.
11.(1)证明:∵EM是△ADE的中线,
∴AM=DM,
∵M是线段BC的中点,
∴BM=CM,
∴AM﹣BM=DM﹣CM,
∴AB=DC,
∴AD﹣AB=AD﹣CD,
∴DB=AC,
在△AEC和△BFD中,
,
∴△AEC≌△BFD(SSS);
(2)解:∵△AEC≌△BFD,
∴∠EAC=∠DBF,
∵∠EDA+∠DBF=∠AED,
∴∠EDA+∠EAD=∠AED,
∵∠EDA+∠EAD+∠AED=180°,
∴∠EDA+∠EAD=∠AED=90°,
∴△AED是直角三角形,
∵EM是△ADE的中线,
∴S△AED=2S△EMD,
∵DH是△EMD中EM边上的高,
∴AE DE=2××EM DH,
∴6×8=2×5DH,
∴DH=.
∴DH的长度为.
12.(1)①证明:∵∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
②解:∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∴∠OAC+∠AOB=∠OBD+∠APB,
∴∠OAC+60°=∠OBD+∠APB,
∴∠APB=60°;
(2)解:由(1)可知:△AOC≌△BOD(SAS),
∴∠OAC=∠OBD,
∴∠OAC+∠AOB=∠OBD+∠APB,
∴∠OAC+α=∠OBD+∠APB,
∴∠APB=α,
∴∠APD=180°﹣α.
故答案为:180°﹣α.
13.(1)解:延长AD,BE交于K点,
∵AD∥BC,
∴∠KAC=∠C,
∵E为AC的中点,
∴AE=CE,
在△AEK与△CEB中,
,
∴△AEK≌△CEB(ASA),
∴AK=BC,
∵BC﹣AB<2BE<BC+AB,
∴1<BE<5;
故答案为:1<BE<5;
(2)证明:∵AD+BD=BC,
∴AD+BD=AK,
∴BD=DK,
∵BE=EK,
∴BE⊥DE.
14.(1)证明:延长EB到G,使BG=DF,连接AG.
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=∠BAD.
∴∠GAE=∠EAF.
又∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD;
(2)(1)中的结论EF=BE+FD,仍然成立,
证明:如图2,延长CB至M,使BM=DF,
∵∠ABC+∠D=180°,∠1+∠ABC=180°,
∴∠1=∠D,
在△ABM与△ADF中,
∴△ABM≌△ADF(SAS).
∴AF=AM,∠2=∠3.
∵∠EAF=∠BAD,
∴∠2+∠4=∠BAD=∠EAF.
∴∠3+∠4=∠EAF,即∠MAE=∠EAF.
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS).
∴EF=ME,即EF=BE+BM,
∴EF=BE+DF.
15.(1)证明:①当P,Q两点分别从B,A两点同时出发运动2秒时,
有BP=2×2=4cm,AQ=4×2=8cm,
∴CP=BC﹣BP=10﹣4=6cm,
CQ=AC﹣AQ=12﹣8=4cm,
∵D是AB的中点,
∴BD=AB=×12=6cm,
∴BP=CQ,BD=CP,
∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
,
∴△BPD≌△CQP(SAS)
②∵△BPD≌△CQP,
∴∠DPB=∠PQC,
∵∠DPB+∠DPQ=∠PQC+∠C,
∴∠DPQ=∠C,
∵∠B=∠C,
∴∠DPQ=∠B;
(2)设当P,Q两点同时出发运动t秒时,
有BP=2t(cm),AQ=4t,CP=(10﹣2t)cm,CQ=(12﹣4t)(cm),
∴PQ=18﹣(10﹣2t)﹣( 12﹣4t)=(6t﹣4)(cm),
∴t的取值范围是0≤t≤3,
要使△CPQ是等腰三角形,则可分为三种情况讨论:
①当CP=CQ时,则有10﹣2t=12﹣4t,
解得:t=1,此时PQ的长度为2cm,不符合题意,
②当PQ=PC时,则有6t﹣4=10﹣2t,
解得:t=;
∴CP=PQ=cm,CQ=5cm,
此时满足△CPQ的周长为18cm;
③当QP=QC时,则有2(12﹣4t)+(10﹣2t)=18,
解得:t=;
∴QP=QC=,PC=,
此时满足△CPQ的周长为18cm;
综上所述,经过s或s时,△CPQ是等腰三角形.
16.(1)证明:在△ACB和△EDB中,
,
∴△ACB≌△EDB(AAS),
∴CA=DE;
(2)证明:如图,过点D作DG∥AB交BC于点G,
∴∠DGB=∠ABC=90°,
∵F是AD的中点,
∴AF=DF,
在△AFB和△DFG中,
,
∴△AFB≌△DFG(AAS),
∴BF=GF,
∴BF=BG,
∵△ACB≌△EDB,
∴AB=DG,
∵AB=EB,
∴EB=DG,
∵△ACB≌△EDB,
∴CB=DB,∠ABC=∠EBD=90°,
∴∠EBC=90°﹣∠DBG,
∵∠GDB=90°﹣∠DBG,
∴∠EBC=∠GDB,
在△EBC和△GDB中,
,
∴△EBC≌△GDB(SAS),
∴EC=GB,
∴BF=EC.
17.(1)证明:如图(1),连接AD,AG,
∵△ABC为等腰直角三角形,
∴∠DAF=∠DBE=45°,且BD=CD=AD,
∵∠AEG=∠AFG=∠ADG=90°,
∴A、E、G、D、F都在以AG为直径的圆上,
∴AEDF内接于圆,
∴∠AFD=180°﹣∠CFD=180°﹣∠AED=∠BED,
在△AFD和△BED中,
,
∴△AFD≌△BED(AAS),
∴ED=FD;
(2)结论DE=DF成立,理由如下:
如图(2),连接AG、AD,在AC上取一点P使∠DFP=∠DPF,
∵∠AEG=∠AFG=∠ADG=90°,
∴A、F、G、D、E都在以AG为直径的圆上,
∴∠DPF=∠DFP=∠AED,
∴∠BED=∠CPD,
在△BED和△CPD中,
,
∴△BED≌△CFD(AAS),
∴DE=DP=DF.
∴DE=DF.
18.(1)证明:∵,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
∴AC=CB,EC=DC,∠ECA=∠DCB,∠B=∠CAB=45°,
在△ECA和△DCB中,
,
∴△ACE≌△BCD.
(2)解:∵△ACE≌△BCD,
∴AE=BD=4,∠CAE=∠B=45°,
∴∠EAD=∠EAC+∠CAB=90°,
∴ED=2.
19.解:(1)如图1,过点B作BT⊥y轴于点T,
∵∠ACB=90°,
∴∠ACO+∠BCT=90°,
∵BT⊥y轴,
∴∠CBT+∠BCT=90°,
∴∠ACO=∠CBT,
在△AOC和△CTB中,
,
∴△AOC≌△CTB(AAS),
∴CT=OA=8,BT=CO=6,
∴OT=2,
∴点B的坐标为(6,﹣2),
故答案为:(6,﹣2);
(2)如图2,过点A作AH⊥OB于H,过点D作DE⊥OB于点E.
∵AO=AB,AH⊥OB,∠OAB=90°,
∴OH=HB,∠AOB=∠ABO=45°,
∴AH=OB=OH=HB,
同(1)可证:△AHC≌△CED(AAS),
∴CH=DE,CE=AH,
∴CE=OH,
∴OE=CH=DE,
∵∠DEO=90°,
∴∠DOE=45°,
∴∠AOD=∠AOB+∠DOE=90°;
(3)如图3,过B作x轴垂线交AC延长线于F,
则∠FAD+∠F=90°,
∵∠FCB=90°,
∴∠FBC+∠F=90°,
∴∠FAD=∠FBC,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(AAS),
∴BF=AD=8+m,
∵AD平分∠BAF,BF⊥x轴,
∴BF=2n,
∴8+m=﹣2n,
∴2n+m=﹣8.
20.(1)证明:如图1所示:
∵∠ABC=∠ACB,
又∵∠DEC=∠ABC+∠BDE,
∠DEC=∠DEF+∠CEF,
∠DEF=∠ABC,
∴∠BDE=∠CEF,
在△DBE和△ECF中,
,
∴△DBE≌△ECF(AAS),
∴DE=EF;
(2)解:∵∠A+2∠DEF=180°,∠A+2∠B=180°,
∴∠DEF=∠B,
∴△DBE≌△ECF(AAS),
∴DB=EC,
∵BC=9,EC=2BE,
∴EC=6,BE=3,
∴BD=EC=6.
(3)解:把(1)中的条件和结论反过来,即:若DE=EF,则∠DEF=∠ABC;这个命题不一定成立.
如图,△BDE和△CEF中,BE=CF,ED=EF.∠B=∠C(SSA),无法判定两个三角形全等.
解答题优生辅导专题训练(附答案)
1.如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH;
(2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
2.如图1,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,连接ED交BC于F,DF=EF.
(1)求证:BD=CE;
(2)如图2,连接CD,若∠DFB=45°,BC=6,求△BCD的面积.
3.已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD、DC(或它们的延长线)于E、F.
(1)当∠MBN绕B点旋转到AE=CF时(如图1),求证:AE+CF=EF;
(2)当∠MBN绕B点旋转到AE≠CF时,在 图2和 图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明.
4.已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
5.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE,垂足为点D,CE⊥AE,垂足为点E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由.
6.已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若A、B两点的坐标分别是A(0,4)、B(﹣2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE=BD.
7.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.
(1)求证:BD=CD.
(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.
(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.
8.综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=40°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF=HF﹣DH.
9.如图BE⊥CD,AB=AD,AC=AE,过A点作AG⊥DE于G,延长GA交BC于F,
(1)求证:F为BC中点;
(2)若AF=12.5,AE=15,求△ADE的面积S△ADE.
10.如图,在△ABC中,AB=AC,点D在边BC上(点D不与点B、点C重合),作∠ADE
=∠B,DE交边AC于点E.
(1)求证:∠BAD=∠CDE;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)当∠B=50°,且△ADE是等腰三角形时,直接写出∠BDA的度数.
11.如图,已知EM是△ADE的中线,B、C是AD边上的两点,且M恰好是线段BC的中点,AE=BF,EC=FD,连接ED.
(1)求证:△AEC≌△BFD;
(2)若∠EDA+∠DBF=∠AED,AE=6,ED=8,EM=5,画出△EMD中EM边上的高DH,并求DH的长度.
12.已知:在△AOB和△COD中,OA=OB,OC=OD.
(1)如图①,若∠AOB=∠COD=60°.
①求证:AC=BD.
②求∠APB的度数.
(2)如图②,若∠AOB=∠COD=α,∠APD的大小为 (直接写出结果,不证明).
13.如图,在△ABC中,AB<BC,过点A作线段AD∥BC,连接BD,且满足AD+BD=BC.取AC的中点E,连接BE、DE.
(1)若AB=4、BC=6,直接写出BE的取值范围 ;
(2)求证:BE⊥DE.
14.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.(1)求证:EF=BE+FD;
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?
15.如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:
①△BPD≌△CQP;
②∠DPQ=∠B;
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ为等腰三角形?
16.如图,在Rt△ABC中,∠ABC=90°,在Rt△EBD中,∠EBD=90°,AB=EB,∠BCA=∠BDE
(1)求证:CA=DE;
(2)连接EC,连接AD,交BC于F,若F恰好是AD的中点,求证:BF=EC.
17.AB=AC,BD=CD,EG⊥AB,GF⊥AC.
(1)若∠BAC=90°,求证ED=FD;
(2)若∠BAC≠90°,则(1)的结论是否成立?
18.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点(不与A、B重合).
(1)求证:△ACE≌△BCD;
(2)若AD=2,BD=4,求ED的长.
19.在平面直角坐标系中,三角形ABC为等腰直角三角形,AC=BC,BC交x轴于点D.
(1)若A(﹣8,0),C(0,6),直接写出点B的坐标 ;
(2)如图2,△OAB与△ACD均为等腰直角三角形,连OD,求∠AOD的度数;
(3)如图3,若AD平分∠BAC,A(﹣8,0),D(m,0),B的纵坐标为n,求2n+m的值.
20.如图,△ABC中,∠ABC=∠ACB,点D、E、F分别是AB、BC、AC边上的点,BE=CF.
(1)若∠DEF=∠ABC,求证:DE=EF;
(2)若∠A+2∠DEF=180°,BC=9,EC=2BE,求BD的长;
(3)把(1)中的条件和结论反过来,即:若DE=EF,则∠DEF=∠ABC;这个命题是否成立?若成立,请证明;若不成立,请说明理由.
参考答案
1.(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵∠ABC=∠GBH,
∴∠A=∠GBH.
∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.
在△ADG和△CDF中,
,
∴△AEF≌△BGH(AAS).
(2)解:∵△AEF≌△BGH,
∴AF=BH,
∴AB=FH=4.
∵EF⊥AB,GH⊥AB,
∴∠EFD=∠GHD.
在△EFD和△GHD中,
∴△EFD≌△GHD(AAS),
∴.
2.(1)证明:如图1,过点D作DG∥AE,交BC于点G,
∴∠FDG=∠E,
在△DGF和△ECF中,
,
∴△DGF≌△ECF(ASA),
∴DG=CE,
∵AB=AC,
∴∠B=∠ACB,
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠DBG=∠DGB,
∴DG=BD,
∴BD=CE;
(2)解:如图2,过点D作DG∥AE,交BC于点G,过点D作DH⊥BC于点H,
∵DB=DG,
∴BH=GH,
由(1)知△DGF≌△ECF,
∴GF=CF,
∴HF=BC=3,
∵DH⊥BC,∠DFB=45°,
∴△DHF是等腰直角三角形,
∴DH=HF=3,
∴S△CDB=BC DH=6×3=9.
3.解:(1)如图1中,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS).
∴BE=BF,∴∠ABE=∠CBF=(∠ABC﹣∠MBN)=(120°﹣60°)=30°.
∴AE=BE,CF=BF,
△BEF是等边三角形.
∴BE=BF=EF.
∴AE+CF=BE+BF=EF;
(2)①如图2中,结论仍然成立.理由如下:
延长DC至K点使得CK=AE,
在△ABE和△CBK中,
,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°,
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
,
∴△EBF≌△KBF(SAS).
∴EF=KF.
∴EF=CK+CF.
∴AE+CF=EF;
③如图3,结论不成立.猜想AE﹣CF=EF,理由如下:
证明如下:在DC的延长线上取点K,使CK=AE,连接BK.
在△ABE和△CBK中,
,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°.
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
,
∴△EBF≌△KBF(SAS),
∴EF=KF,
∴EF=CK﹣CF.
∴AE﹣CF=EF.
4.解:(1)∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
,
∴△FAD≌△DBC(SAS);
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形.
(2)如图2,作AF⊥AB于A,使AF=BD,连接DF,CF,
∴∠FAD=90°.
∵∠ABC=90°,
∴∠FAD=∠DBC=90°.
在△FAD和△DBC中,
,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°.
∵∠APD=45°,
∴∠FCD=∠APD,
∴CF∥AE.
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,
∴CE=BD.
5.证明:(1)∵∠BAC=90°,
∴∠2+∠3=90°,
∵BD⊥AE,
∴∠1+∠3=90°,
∴∠1=∠2,
在△ABD和△CAE中,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE﹣CE,
理由如下:∵∠BAC=90°,
∴∠1+∠3=90°,
∵BD⊥AE,
∴∠1+∠2=90°,
∴∠2=∠3,
在△ABD和△CAE中,
,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∵AE=DE﹣AD,
∴BD=DE﹣CE.
6.解:(1)如图1中,作CM⊥OA垂足为M,则∠AMC=90°,
∵∠BAC=∠AOB=90°,
∴∠BAO+∠CAM=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠CAM,
在△ABO和△CAM中,
,
∴△ABO≌△CAM(AAS),
∴MC=AO,AM=BO,
∵A(0,4)、B(﹣2,0),
∴AO=4,BO=2,
∴MC=4,AM=2,MO=AO﹣AM=2,
∴点C坐标(4,2);
(2)如图2,延长CE、BA相交于点F,
∵BE⊥CE,∠BAC=90°,
∴∠EBF+∠F=90°,∠ACF+∠F=90°,
∴∠EBF=∠ACF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵BE⊥CF,BE平分∠FBC,
∴△BCF是等腰三角形,CF是底边,
∴CE=,
∴CE=BD.
7.(1)证明:∵∠A=120°,∠C=20°,
∴∠ABC=180°﹣120°﹣20°=40°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=ABC=20°,
∴∠DBC=∠C=20°,
∴BD=CD;
(2)证明:如图2,过点E作EF∥BD交AC于点F,
∴∠FEC=∠DBC=20°,
∴∠FEC=∠C=20°,
∴∠AFE=40°,FE=FC,
∴∠AFE=∠ABC,
∵AE是∠BAC的平分线,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS),
∴BE=EF,
∴BE=EF=FC,
∴AB+BE=AF+FC=AC;
(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:
如图3,过点A作AF∥BD交BE于点F,
∴∠AFC=∠DBC=20°,
∴∠AFC=∠C=20°,
∴AF=AC,
∵AE是∠BAC的外角平分线,
∴∠EAB=(180°﹣∠ABC)=30°,
∵∠ABC=40°,
∴∠E=∠ABC﹣∠EAB=10°,
∴∠E=∠FAE=10°,
∴FE=AF,
∴FE=AF=AC,
∴BE﹣AB=BE﹣BF=EF=AC.
8.(1)证明:∵∠BAC=∠DAE.
∴∠CAE=∠BAD.
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴∠AEC=∠ADB,
∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,
∵∠BFC+∠DFE=180°,
∴∠BFC=∠DAE=∠BAC=40°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.
∵△ACE≌△ABD,
∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD,
∴CE AJ=BD AH,
∴AJ=AH,
在Rt△AFJ和Rt△AFH中,
,
∴Rt△AFJ≌Rt△AFH(HL),
∴FJ=FH,
在Rt△AJE和Rt△AHD中,
,
∴Rt△AJE≌Rt△AHD(HL),
∴EJ=DH,
∴EF=FJ﹣EJ=FH﹣DH.
∴EF=HF﹣DH.
9.(1)证明:∵BE⊥CD,
∴∠DAE=∠DAB=∠BAC=∠CAE=90°,
在△ADE和△ABC中,
,
∴△ADE≌△ABC (SAS),
∴∠DEA=∠BCA,
∵AG⊥DE,
∴∠AGD=90°,
∴∠AED+∠ADE=∠DAG+∠ADE=90°,
∴∠AED=∠DAG,
∵∠DAG=∠CAF,
∴∠CAF=∠FCA,
∴FC=FA,
∵∠BAC=90°,
∴∠FAC+∠BAF=∠FCA+∠FBA=90°,
∴∠BAF=∠FBA,
∴FB=FA,
∴FB=FC,
∴F是BC的中点;
(2)解:∵F为BC的中点,∠BAC=90°,
∴AF=BC,
∴BC=2AF=25,
由△ABC≌△ADE知:DE=BC=25,
∵AE=15,∠DAE=90°,
∴AD=20,
∴S△ADE=AD AE=20×15=150.
10.(1)证明:∠ADE=∠B,∠BAD+∠B=∠ADC,∠CDE+∠ADE=∠ADC,
∴∠BAD=∠CDE;
(2)证明:∵AB=AC,
∴∠B=∠C,
∵DC=AB,∠BAD=∠CDE;
在△ABD和△DCE中,
,
∴△ABD≌△DCE(SAS);
(3)解:∵∠B=∠C=50°,∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣50°=80°,
分三种情况讨论:
①当DA=DE时,∠DAE=∠DEA,
∵∠ADE=∠B=50°,∠ADE+∠DAE+∠DEA=180°,
∴∠DAE=(180°﹣50°)÷2=65°,
∴∠BAD=∠BAC﹣∠DAE=80°﹣65°=15°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°﹣∠B﹣∠BAD=180°﹣50°﹣15°=115°;
②当AD=AE时,∠AED=∠ADE=50°,
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°﹣∠AED﹣∠ADE=180°﹣50°﹣50°=80°,
∵∠BAC=80°,
∴∠DAE=∠BAE,
∴点D与点B重合,不合题意.
③当EA=ED时,∠DAE=∠ADE=50°,
∴∠BAD=∠BAC﹣∠DAE=80°﹣50°=30°,
∵∠B+∠BAD+∠BDA=180°,
∴∠BDA=180°﹣∠B﹣∠BAD=180°﹣50°﹣30°=100°,
综上所述,当∠BDA的度数为115°或100°时,△ADE是等腰三角形.
11.(1)证明:∵EM是△ADE的中线,
∴AM=DM,
∵M是线段BC的中点,
∴BM=CM,
∴AM﹣BM=DM﹣CM,
∴AB=DC,
∴AD﹣AB=AD﹣CD,
∴DB=AC,
在△AEC和△BFD中,
,
∴△AEC≌△BFD(SSS);
(2)解:∵△AEC≌△BFD,
∴∠EAC=∠DBF,
∵∠EDA+∠DBF=∠AED,
∴∠EDA+∠EAD=∠AED,
∵∠EDA+∠EAD+∠AED=180°,
∴∠EDA+∠EAD=∠AED=90°,
∴△AED是直角三角形,
∵EM是△ADE的中线,
∴S△AED=2S△EMD,
∵DH是△EMD中EM边上的高,
∴AE DE=2××EM DH,
∴6×8=2×5DH,
∴DH=.
∴DH的长度为.
12.(1)①证明:∵∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
②解:∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∴∠OAC+∠AOB=∠OBD+∠APB,
∴∠OAC+60°=∠OBD+∠APB,
∴∠APB=60°;
(2)解:由(1)可知:△AOC≌△BOD(SAS),
∴∠OAC=∠OBD,
∴∠OAC+∠AOB=∠OBD+∠APB,
∴∠OAC+α=∠OBD+∠APB,
∴∠APB=α,
∴∠APD=180°﹣α.
故答案为:180°﹣α.
13.(1)解:延长AD,BE交于K点,
∵AD∥BC,
∴∠KAC=∠C,
∵E为AC的中点,
∴AE=CE,
在△AEK与△CEB中,
,
∴△AEK≌△CEB(ASA),
∴AK=BC,
∵BC﹣AB<2BE<BC+AB,
∴1<BE<5;
故答案为:1<BE<5;
(2)证明:∵AD+BD=BC,
∴AD+BD=AK,
∴BD=DK,
∵BE=EK,
∴BE⊥DE.
14.(1)证明:延长EB到G,使BG=DF,连接AG.
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=∠BAD.
∴∠GAE=∠EAF.
又∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD;
(2)(1)中的结论EF=BE+FD,仍然成立,
证明:如图2,延长CB至M,使BM=DF,
∵∠ABC+∠D=180°,∠1+∠ABC=180°,
∴∠1=∠D,
在△ABM与△ADF中,
∴△ABM≌△ADF(SAS).
∴AF=AM,∠2=∠3.
∵∠EAF=∠BAD,
∴∠2+∠4=∠BAD=∠EAF.
∴∠3+∠4=∠EAF,即∠MAE=∠EAF.
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS).
∴EF=ME,即EF=BE+BM,
∴EF=BE+DF.
15.(1)证明:①当P,Q两点分别从B,A两点同时出发运动2秒时,
有BP=2×2=4cm,AQ=4×2=8cm,
∴CP=BC﹣BP=10﹣4=6cm,
CQ=AC﹣AQ=12﹣8=4cm,
∵D是AB的中点,
∴BD=AB=×12=6cm,
∴BP=CQ,BD=CP,
∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
,
∴△BPD≌△CQP(SAS)
②∵△BPD≌△CQP,
∴∠DPB=∠PQC,
∵∠DPB+∠DPQ=∠PQC+∠C,
∴∠DPQ=∠C,
∵∠B=∠C,
∴∠DPQ=∠B;
(2)设当P,Q两点同时出发运动t秒时,
有BP=2t(cm),AQ=4t,CP=(10﹣2t)cm,CQ=(12﹣4t)(cm),
∴PQ=18﹣(10﹣2t)﹣( 12﹣4t)=(6t﹣4)(cm),
∴t的取值范围是0≤t≤3,
要使△CPQ是等腰三角形,则可分为三种情况讨论:
①当CP=CQ时,则有10﹣2t=12﹣4t,
解得:t=1,此时PQ的长度为2cm,不符合题意,
②当PQ=PC时,则有6t﹣4=10﹣2t,
解得:t=;
∴CP=PQ=cm,CQ=5cm,
此时满足△CPQ的周长为18cm;
③当QP=QC时,则有2(12﹣4t)+(10﹣2t)=18,
解得:t=;
∴QP=QC=,PC=,
此时满足△CPQ的周长为18cm;
综上所述,经过s或s时,△CPQ是等腰三角形.
16.(1)证明:在△ACB和△EDB中,
,
∴△ACB≌△EDB(AAS),
∴CA=DE;
(2)证明:如图,过点D作DG∥AB交BC于点G,
∴∠DGB=∠ABC=90°,
∵F是AD的中点,
∴AF=DF,
在△AFB和△DFG中,
,
∴△AFB≌△DFG(AAS),
∴BF=GF,
∴BF=BG,
∵△ACB≌△EDB,
∴AB=DG,
∵AB=EB,
∴EB=DG,
∵△ACB≌△EDB,
∴CB=DB,∠ABC=∠EBD=90°,
∴∠EBC=90°﹣∠DBG,
∵∠GDB=90°﹣∠DBG,
∴∠EBC=∠GDB,
在△EBC和△GDB中,
,
∴△EBC≌△GDB(SAS),
∴EC=GB,
∴BF=EC.
17.(1)证明:如图(1),连接AD,AG,
∵△ABC为等腰直角三角形,
∴∠DAF=∠DBE=45°,且BD=CD=AD,
∵∠AEG=∠AFG=∠ADG=90°,
∴A、E、G、D、F都在以AG为直径的圆上,
∴AEDF内接于圆,
∴∠AFD=180°﹣∠CFD=180°﹣∠AED=∠BED,
在△AFD和△BED中,
,
∴△AFD≌△BED(AAS),
∴ED=FD;
(2)结论DE=DF成立,理由如下:
如图(2),连接AG、AD,在AC上取一点P使∠DFP=∠DPF,
∵∠AEG=∠AFG=∠ADG=90°,
∴A、F、G、D、E都在以AG为直径的圆上,
∴∠DPF=∠DFP=∠AED,
∴∠BED=∠CPD,
在△BED和△CPD中,
,
∴△BED≌△CFD(AAS),
∴DE=DP=DF.
∴DE=DF.
18.(1)证明:∵,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
∴AC=CB,EC=DC,∠ECA=∠DCB,∠B=∠CAB=45°,
在△ECA和△DCB中,
,
∴△ACE≌△BCD.
(2)解:∵△ACE≌△BCD,
∴AE=BD=4,∠CAE=∠B=45°,
∴∠EAD=∠EAC+∠CAB=90°,
∴ED=2.
19.解:(1)如图1,过点B作BT⊥y轴于点T,
∵∠ACB=90°,
∴∠ACO+∠BCT=90°,
∵BT⊥y轴,
∴∠CBT+∠BCT=90°,
∴∠ACO=∠CBT,
在△AOC和△CTB中,
,
∴△AOC≌△CTB(AAS),
∴CT=OA=8,BT=CO=6,
∴OT=2,
∴点B的坐标为(6,﹣2),
故答案为:(6,﹣2);
(2)如图2,过点A作AH⊥OB于H,过点D作DE⊥OB于点E.
∵AO=AB,AH⊥OB,∠OAB=90°,
∴OH=HB,∠AOB=∠ABO=45°,
∴AH=OB=OH=HB,
同(1)可证:△AHC≌△CED(AAS),
∴CH=DE,CE=AH,
∴CE=OH,
∴OE=CH=DE,
∵∠DEO=90°,
∴∠DOE=45°,
∴∠AOD=∠AOB+∠DOE=90°;
(3)如图3,过B作x轴垂线交AC延长线于F,
则∠FAD+∠F=90°,
∵∠FCB=90°,
∴∠FBC+∠F=90°,
∴∠FAD=∠FBC,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(AAS),
∴BF=AD=8+m,
∵AD平分∠BAF,BF⊥x轴,
∴BF=2n,
∴8+m=﹣2n,
∴2n+m=﹣8.
20.(1)证明:如图1所示:
∵∠ABC=∠ACB,
又∵∠DEC=∠ABC+∠BDE,
∠DEC=∠DEF+∠CEF,
∠DEF=∠ABC,
∴∠BDE=∠CEF,
在△DBE和△ECF中,
,
∴△DBE≌△ECF(AAS),
∴DE=EF;
(2)解:∵∠A+2∠DEF=180°,∠A+2∠B=180°,
∴∠DEF=∠B,
∴△DBE≌△ECF(AAS),
∴DB=EC,
∵BC=9,EC=2BE,
∴EC=6,BE=3,
∴BD=EC=6.
(3)解:把(1)中的条件和结论反过来,即:若DE=EF,则∠DEF=∠ABC;这个命题不一定成立.
如图,△BDE和△CEF中,BE=CF,ED=EF.∠B=∠C(SSA),无法判定两个三角形全等.
