24.1.4圆周角 同步测试题 2023-2024学年人教版九年级数学上册(含答案)
文档属性
| 名称 | 24.1.4圆周角 同步测试题 2023-2024学年人教版九年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 411.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


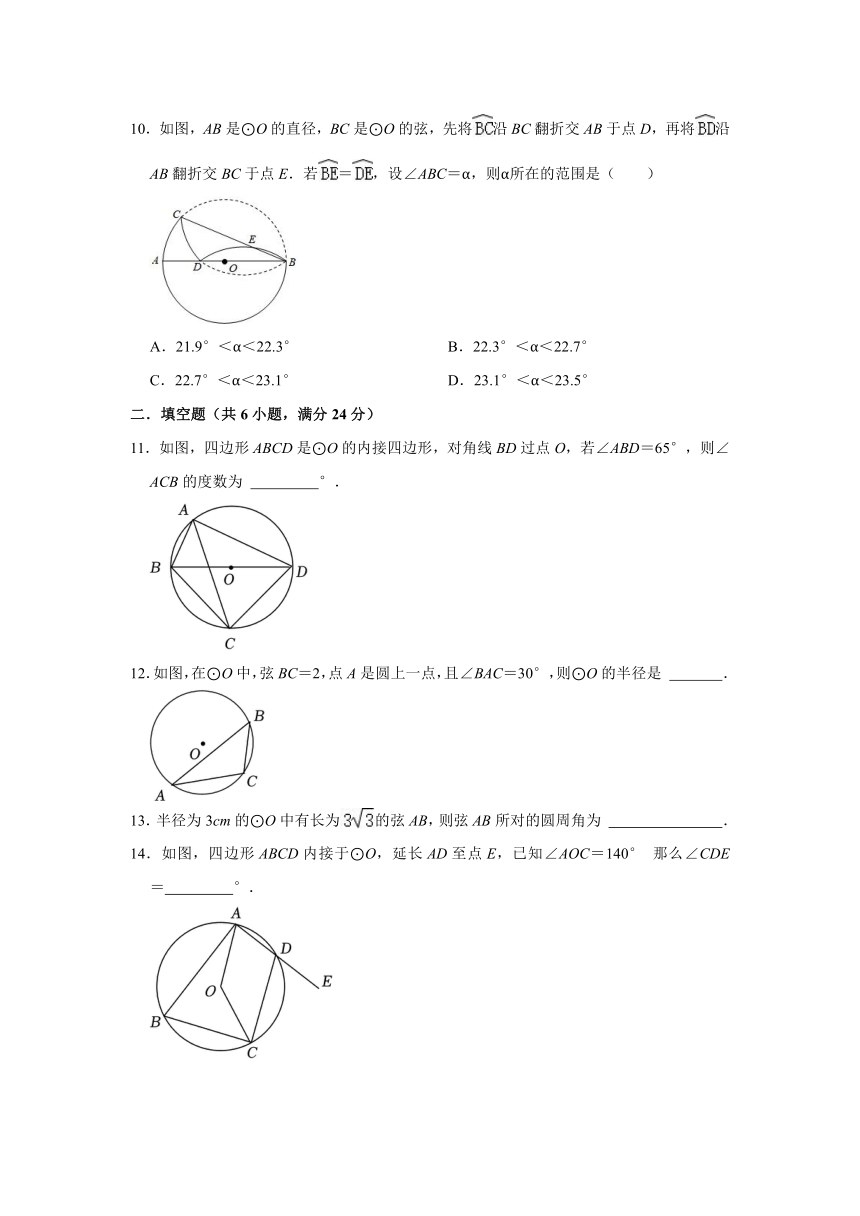
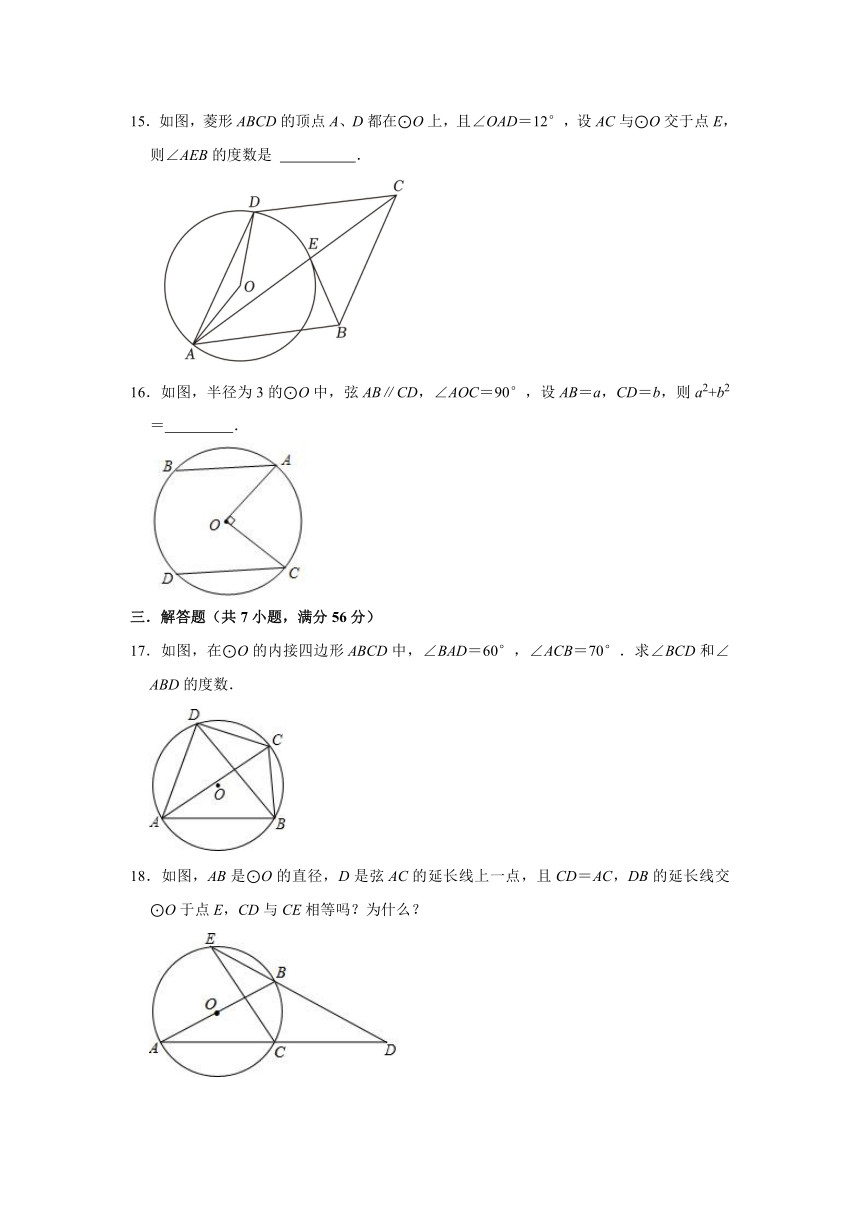

文档简介
2023-2024学年人教版九年级数学上册《24.1.4圆周角》同步测试题(附答案)
一.选择题(共10小题,满分40分)
1.如图,AB是⊙O的直径,AC、BC是⊙O的弦,若∠A=30°,则∠B的度数为( )
A.70° B.90° C.40° D.60°
2.如图,AB是⊙O的直径,若AC=4,∠D=60°,则BC的长等于( )
A.8 B.10 C.2 D.4
3.下列语句中不正确的有( )
①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤圆内接四边形的对角互补;⑥在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.
A.5个 B.4个 C.3个 D.2个
4.如图,AB是⊙O的直径,AC为弦,∠BAC=25°,在⊙O上任取一点D,且点D与点C位于直径AB的两侧,连接AD和DC,则∠D的度数是( )
A.50° B.60° C.65° D.75°
5.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,连结AO,BO,则∠AOB的度数是( )
A.30° B.60° C.80° D.90°
6.如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=82°,那么∠BOD的度数为( )
A.160° B.162° C.164° D.170°
7.如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为( )
A.5 B.10 C.5 D.10
8.如图,已知四边形ABCD内接于⊙O,=,AD、BC的延长线相交于点E,AF为直径,连接BF.若∠BAF=32°,∠E=40°,则∠CBF的度数为( )
A.16° B.24° C.12° D.14°
9.如图是以O为圆心,AB为直径的圆形纸片,点C在⊙O上.将该纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E,若AD=ED,则∠B的度数为( )
A.24° B.30° C.36° D.44°
10.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是( )
A.21.9°<α<22.3° B.22.3°<α<22.7°
C.22.7°<α<23.1° D.23.1°<α<23.5°
二.填空题(共6小题,满分24分)
11.如图,四边形ABCD是⊙O的内接四边形,对角线BD过点O,若∠ABD=65°,则∠ACB的度数为 °.
12.如图,在⊙O中,弦BC=2,点A是圆上一点,且∠BAC=30°,则⊙O的半径是 .
13.半径为3cm的⊙O中有长为的弦AB,则弦AB所对的圆周角为 .
14.如图,四边形ABCD内接于⊙O,延长AD至点E,已知∠AOC=140° 那么∠CDE= °.
15.如图,菱形ABCD的顶点A、D都在⊙O上,且∠OAD=12°,设AC与⊙O交于点E,则∠AEB的度数是 .
16.如图,半径为3的⊙O中,弦AB∥CD,∠AOC=90°,设AB=a,CD=b,则a2+b2= .
三.解答题(共7小题,满分56分)
17.如图,在⊙O的内接四边形ABCD中,∠BAD=60°,∠ACB=70°.求∠BCD和∠ABD的度数.
18.如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E,CD与CE相等吗?为什么?
19.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=45°,∠APD=75°.
(1)求∠B的大小;
(2)已知圆心O到BD的距离为3,求AD的长.
20.如图,点A、B、C在⊙O上,BC是直径,∠ABC的角平分线BD与⊙O交于点D,与AC交于点M,且BM=MD,连接OD,交AC于点N.
(1)证明:OD⊥AC;
(2)试猜想AB与OD之间的数量关系,并证明.
21.如图,四边形ABCD是⊙O的内接四边形,且对角线BD经过⊙O的圆心O,过点A作AE⊥CD,与CD的延长线交于点E,且DA平分∠BDE.
(1)求证:∠ABO=∠EAD;
(2)若⊙O的半径为5,CD=6,求AD的长.
22.在圆⊙O中,AB为弦(不是直径),K为弧AB的中点,C为优弧AB上一点,连接KC交AB于M
(1)如图1,作直径CT,连接KT,求证:∠KTC=∠KMB;
(2)如图2,作直径AD交KC于N,若∠ADC=45°,求证:AN=AM.
23.如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵AB是⊙O的直径,
∴∠C=90°,
∵∠A=30°,
∴∠B=90°﹣∠A=60°,
故选:D.
2.解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠D=60°,∠A=∠D,
∴∠A=60°,
∴∠ABC=90°﹣∠A=30°,
∵AC=4,
∴AB=2AC=8,
∴BC2===4,
故选:D.
3.解:①平分弦(不是直径)的直径垂直于弦,本说法错误;
②在同圆或等圆中,相等的圆心角所对的弧相等,本说法错误;
③能够完全重合的两条弧是等弧,本说法错误;
④圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,本说法错误;
⑤圆内接四边形的对角互补,本说法正确;
⑥在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等或互补,本说法错误;
故选:A.
4.解:连接BC,如图所示,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=65°,
∵,
∴∠D=∠B=65°.
故选:C.
5.解:∵∠P=30°,
又∵∠AOB=2∠P,
∴∠AOB=60°,
故选:B.
6.解:∵∠DCE+∠BCD=180°,∠A+∠BCD=180°,
∴∠A=∠BCD,
∵∠BCD=82°,
∴∠A=82°,
∴∠BOD=164°.
故选:C.
7.解:∵AC=AC,
∴∠D=∠B,
∵∠BAC=∠D,
∴∠B=∠BAC,
∴△ABC是等腰三角形,
∵AB是直径,
∴△ABC是等腰直角三角形,
∵AC=5,
∴AB=5,
故选:C.
8.解:∵AF为圆的直径,
∴∠ABF=90°,=,
∵=,
∴=,
∴∠DAF=∠BAF=32°,
∴∠BAD=64°,
∵∠E=40°,
∴∠ABC=180°﹣∠BAD﹣∠E=76°,
∴∠CBF=∠ABF﹣∠ABC=14°.
故选:D.
9.解:∵AD=DE,
∴∠DAE=∠DEA,
∵∠DEA=∠BEC,∠DAE=∠BCE,
∴∠BEC=∠BCE,
∵将该圆形纸片沿直线CO对折,
∴∠ECO=∠BCO,
又∵OB=OC,
∴∠OCB=∠B,
设∠ECO=∠OCB=∠B=x,
∴∠BCE=∠ECO+∠BCO=2x,
∴∠CEB=2x,
∵∠BEC+∠BCE+∠B=180°,
∴x+2x+2x=180°,
∴x=36°,
∴∠B=36°;
故选:C.
10.解:如图,连接AC,CD,DE.
∵=,
∴ED=EB,
∴∠EDB=∠EBD=α,
∵==(对着同一个圆周角),
∴AC=CD=DE,
∴∠DCE=∠DEC=∠EDB+∠EBD=2α,
∴∠CAD=∠CDA=∠DCE+∠EBD=3α,
∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴4α=90°,
∴α=22.5°,
故选:B.
二.填空题(共6小题,满分24分)
11.解:∵BD是⊙O的直径,
∴∠BCD=90°,
∵∠ABD=65°,∠ABD=∠ACD,
∴∠ACD=65°,
∵∠ACB+∠ACD=∠BCD,
∴∠ACB=25°,
故答案为:25.
12.解:连接OB、OC,如图,
∵∠BOC=2∠BAC=2×30°=60°,
而OB=OC,
∴△OBC为等边三角形,
∴OB=BC=2,
即⊙O的半径为2.
故答案为:2.
13.解:连接OA,OB,作OD⊥AB,
∵OA=3cm,AB=3cm,
∴AD=BD=,
∴AD:OA=:2,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠AMB=60°,
∴∠ANB=120°.
∴弦AB所对的圆周角度数为60°或120°.
故答案为:60°或120°.
14.解:∵∠CDE+∠ADC=180°,∠B+∠ADC=180°,
∴∠CDE=∠B,
∵∠B=∠AOC=×140°=70°,
∴∠CDE=70°.
故答案为:70.
15.解:如图,连接DE,
∵OA=OD,
∴∠ODA=∠OAD=12°,
∴∠AOD=180°﹣12°﹣12°=156°,
∴∠AED=∠AOD=78°,
∵四边形ABCD是菱形,
∴AB=AD,∠BAE=∠DAE,
在△BAE和△DAE中,
,
∴△BAE≌△DAE(SAS),
∴∠AEB=∠AED=78°,
故答案为:78°.
16.解:如图,过点O作OM⊥AB于点M交CD于点N.
∵AB∥CD,OM⊥AB,
∴ON⊥CD,
∴AM=AB=a,CN=CD=b,
∵∠AOC=∠AMO=∠CNO=90°,
∴∠AOM+∠CON=90°,∠CON+∠OCN=90°,
∴∠AOM=∠OCN,
在△AMO和△ONC中,
,
∴△AMO≌△ONC(AAS),
∴OM=CN=b,
∵OA2=AM2+OM2,
∴32=(a)2+(b)2,
∴a2+b2=36.
故答案为:36.
三.解答题(共7小题,满分56分)
17.解:∵在⊙O的内接四边形ABCD中,∠BAD=60°,
∴∠BCD=180°﹣∠BAD=120°,
∵∠ACB=70°,
∴∠ACD=∠BCD﹣∠ACB=50°,
∴∠ABD=∠ACD=50°.
18.解:CD与CE相等;
理由:连接BC,
∵AB是⊙O的直径,
∴∠ABC=90°,即BC⊥AD,
∵CD=AC,
∴AB=BD,
∴∠A=∠D,
∴∠CEB=∠A,
∴∠CEB=∠D,
∴CE=CD.
19.解:(1)∵∠CAB=45°,∠APD=75°.
∴∠C=∠APD﹣∠CAB=30°,
∵由圆周角定理得:∠C=∠B,
∴∠B=30°;
(2)过O作OE⊥BD于E,
∵OE过O,
∴BE=DE,
∵圆心O到BD的距离为3,
∴OE=3,
∵AO=BO,DE=BE,
∴AD=2OE=6.
20.(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBO,
∴,
∴OD⊥AC;
(2)解:猜想 OD=AB.
∵,OD⊥AC,
∴AN=NC.
∵,AN=NC,
∴ON是△ABC 的中位线,
∴AB=2ON,AB∥ON.
∴∠ABM=∠NDM.
∵BM=MD,∠BMA=∠DMN,
∴△ABM≌△NDM(ASA),
∴AB=ND=2ON.
∴OD=ON+ND=AB.
21.(1)证明:∵BD为直径,
∴∠BAD=90°,
∴∠ABD+∠ADB=90°,
∵AE⊥CE,
∴∠ADE+∠EAD=90°,
∵DA平分∠BDE,
∴∠ADB=∠ADE,
∴∠ABD=∠EAD,
即∠ABO=∠EAD;
(2)解:过O点作OH⊥CD于H点,连接OA,如图,则CH=DH=CD=3,
在Rt△ODH中,OH===4,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠ODA=∠ADE,
∴∠OAD=∠ADE,
∴OA∥CE,
∴∠OAE=180°﹣∠E=90°,
∵∠OHE=∠E=∠OAE=90°,
∴四边形OAEH为矩形,
∴AE=OH=4,HE=OA=5,
∴DE=5﹣3=2,
在Rt△ADE中,AD===2.
22.证明:(1)连接AK,如图1,
∵K为弧AB的中点,
∴=,
∴=+=+,
∵∠KMB=∠A+∠AKM,
而∠A对,∠AKC对,
∴∠KTC=∠KMB;
(2)连接OC,如图2,
∵K为弧AB的中点,
∴OK⊥AB,
∴∠K+∠KMB=90°,
∵OC=OD,∠D=45°,
∴∠COD=90°,
∴∠OCK+∠ONC=90°,
而OK=OC,
∴∠K=∠OCK,
∴∠KMB=∠ONC,
∵∠KMB=∠AMN,∠ONC=∠ANM,
∴∠AMN=∠ANM,
∴AM=AN.
23.解:(1)如图1,
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.理由如下:
如图2,设∠ABE=α,∠CBF=β,
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
一.选择题(共10小题,满分40分)
1.如图,AB是⊙O的直径,AC、BC是⊙O的弦,若∠A=30°,则∠B的度数为( )
A.70° B.90° C.40° D.60°
2.如图,AB是⊙O的直径,若AC=4,∠D=60°,则BC的长等于( )
A.8 B.10 C.2 D.4
3.下列语句中不正确的有( )
①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤圆内接四边形的对角互补;⑥在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.
A.5个 B.4个 C.3个 D.2个
4.如图,AB是⊙O的直径,AC为弦,∠BAC=25°,在⊙O上任取一点D,且点D与点C位于直径AB的两侧,连接AD和DC,则∠D的度数是( )
A.50° B.60° C.65° D.75°
5.如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,连结AO,BO,则∠AOB的度数是( )
A.30° B.60° C.80° D.90°
6.如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=82°,那么∠BOD的度数为( )
A.160° B.162° C.164° D.170°
7.如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为( )
A.5 B.10 C.5 D.10
8.如图,已知四边形ABCD内接于⊙O,=,AD、BC的延长线相交于点E,AF为直径,连接BF.若∠BAF=32°,∠E=40°,则∠CBF的度数为( )
A.16° B.24° C.12° D.14°
9.如图是以O为圆心,AB为直径的圆形纸片,点C在⊙O上.将该纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E,若AD=ED,则∠B的度数为( )
A.24° B.30° C.36° D.44°
10.如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是( )
A.21.9°<α<22.3° B.22.3°<α<22.7°
C.22.7°<α<23.1° D.23.1°<α<23.5°
二.填空题(共6小题,满分24分)
11.如图,四边形ABCD是⊙O的内接四边形,对角线BD过点O,若∠ABD=65°,则∠ACB的度数为 °.
12.如图,在⊙O中,弦BC=2,点A是圆上一点,且∠BAC=30°,则⊙O的半径是 .
13.半径为3cm的⊙O中有长为的弦AB,则弦AB所对的圆周角为 .
14.如图,四边形ABCD内接于⊙O,延长AD至点E,已知∠AOC=140° 那么∠CDE= °.
15.如图,菱形ABCD的顶点A、D都在⊙O上,且∠OAD=12°,设AC与⊙O交于点E,则∠AEB的度数是 .
16.如图,半径为3的⊙O中,弦AB∥CD,∠AOC=90°,设AB=a,CD=b,则a2+b2= .
三.解答题(共7小题,满分56分)
17.如图,在⊙O的内接四边形ABCD中,∠BAD=60°,∠ACB=70°.求∠BCD和∠ABD的度数.
18.如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E,CD与CE相等吗?为什么?
19.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=45°,∠APD=75°.
(1)求∠B的大小;
(2)已知圆心O到BD的距离为3,求AD的长.
20.如图,点A、B、C在⊙O上,BC是直径,∠ABC的角平分线BD与⊙O交于点D,与AC交于点M,且BM=MD,连接OD,交AC于点N.
(1)证明:OD⊥AC;
(2)试猜想AB与OD之间的数量关系,并证明.
21.如图,四边形ABCD是⊙O的内接四边形,且对角线BD经过⊙O的圆心O,过点A作AE⊥CD,与CD的延长线交于点E,且DA平分∠BDE.
(1)求证:∠ABO=∠EAD;
(2)若⊙O的半径为5,CD=6,求AD的长.
22.在圆⊙O中,AB为弦(不是直径),K为弧AB的中点,C为优弧AB上一点,连接KC交AB于M
(1)如图1,作直径CT,连接KT,求证:∠KTC=∠KMB;
(2)如图2,作直径AD交KC于N,若∠ADC=45°,求证:AN=AM.
23.如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵AB是⊙O的直径,
∴∠C=90°,
∵∠A=30°,
∴∠B=90°﹣∠A=60°,
故选:D.
2.解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠D=60°,∠A=∠D,
∴∠A=60°,
∴∠ABC=90°﹣∠A=30°,
∵AC=4,
∴AB=2AC=8,
∴BC2===4,
故选:D.
3.解:①平分弦(不是直径)的直径垂直于弦,本说法错误;
②在同圆或等圆中,相等的圆心角所对的弧相等,本说法错误;
③能够完全重合的两条弧是等弧,本说法错误;
④圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,本说法错误;
⑤圆内接四边形的对角互补,本说法正确;
⑥在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等或互补,本说法错误;
故选:A.
4.解:连接BC,如图所示,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=65°,
∵,
∴∠D=∠B=65°.
故选:C.
5.解:∵∠P=30°,
又∵∠AOB=2∠P,
∴∠AOB=60°,
故选:B.
6.解:∵∠DCE+∠BCD=180°,∠A+∠BCD=180°,
∴∠A=∠BCD,
∵∠BCD=82°,
∴∠A=82°,
∴∠BOD=164°.
故选:C.
7.解:∵AC=AC,
∴∠D=∠B,
∵∠BAC=∠D,
∴∠B=∠BAC,
∴△ABC是等腰三角形,
∵AB是直径,
∴△ABC是等腰直角三角形,
∵AC=5,
∴AB=5,
故选:C.
8.解:∵AF为圆的直径,
∴∠ABF=90°,=,
∵=,
∴=,
∴∠DAF=∠BAF=32°,
∴∠BAD=64°,
∵∠E=40°,
∴∠ABC=180°﹣∠BAD﹣∠E=76°,
∴∠CBF=∠ABF﹣∠ABC=14°.
故选:D.
9.解:∵AD=DE,
∴∠DAE=∠DEA,
∵∠DEA=∠BEC,∠DAE=∠BCE,
∴∠BEC=∠BCE,
∵将该圆形纸片沿直线CO对折,
∴∠ECO=∠BCO,
又∵OB=OC,
∴∠OCB=∠B,
设∠ECO=∠OCB=∠B=x,
∴∠BCE=∠ECO+∠BCO=2x,
∴∠CEB=2x,
∵∠BEC+∠BCE+∠B=180°,
∴x+2x+2x=180°,
∴x=36°,
∴∠B=36°;
故选:C.
10.解:如图,连接AC,CD,DE.
∵=,
∴ED=EB,
∴∠EDB=∠EBD=α,
∵==(对着同一个圆周角),
∴AC=CD=DE,
∴∠DCE=∠DEC=∠EDB+∠EBD=2α,
∴∠CAD=∠CDA=∠DCE+∠EBD=3α,
∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴4α=90°,
∴α=22.5°,
故选:B.
二.填空题(共6小题,满分24分)
11.解:∵BD是⊙O的直径,
∴∠BCD=90°,
∵∠ABD=65°,∠ABD=∠ACD,
∴∠ACD=65°,
∵∠ACB+∠ACD=∠BCD,
∴∠ACB=25°,
故答案为:25.
12.解:连接OB、OC,如图,
∵∠BOC=2∠BAC=2×30°=60°,
而OB=OC,
∴△OBC为等边三角形,
∴OB=BC=2,
即⊙O的半径为2.
故答案为:2.
13.解:连接OA,OB,作OD⊥AB,
∵OA=3cm,AB=3cm,
∴AD=BD=,
∴AD:OA=:2,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠AMB=60°,
∴∠ANB=120°.
∴弦AB所对的圆周角度数为60°或120°.
故答案为:60°或120°.
14.解:∵∠CDE+∠ADC=180°,∠B+∠ADC=180°,
∴∠CDE=∠B,
∵∠B=∠AOC=×140°=70°,
∴∠CDE=70°.
故答案为:70.
15.解:如图,连接DE,
∵OA=OD,
∴∠ODA=∠OAD=12°,
∴∠AOD=180°﹣12°﹣12°=156°,
∴∠AED=∠AOD=78°,
∵四边形ABCD是菱形,
∴AB=AD,∠BAE=∠DAE,
在△BAE和△DAE中,
,
∴△BAE≌△DAE(SAS),
∴∠AEB=∠AED=78°,
故答案为:78°.
16.解:如图,过点O作OM⊥AB于点M交CD于点N.
∵AB∥CD,OM⊥AB,
∴ON⊥CD,
∴AM=AB=a,CN=CD=b,
∵∠AOC=∠AMO=∠CNO=90°,
∴∠AOM+∠CON=90°,∠CON+∠OCN=90°,
∴∠AOM=∠OCN,
在△AMO和△ONC中,
,
∴△AMO≌△ONC(AAS),
∴OM=CN=b,
∵OA2=AM2+OM2,
∴32=(a)2+(b)2,
∴a2+b2=36.
故答案为:36.
三.解答题(共7小题,满分56分)
17.解:∵在⊙O的内接四边形ABCD中,∠BAD=60°,
∴∠BCD=180°﹣∠BAD=120°,
∵∠ACB=70°,
∴∠ACD=∠BCD﹣∠ACB=50°,
∴∠ABD=∠ACD=50°.
18.解:CD与CE相等;
理由:连接BC,
∵AB是⊙O的直径,
∴∠ABC=90°,即BC⊥AD,
∵CD=AC,
∴AB=BD,
∴∠A=∠D,
∴∠CEB=∠A,
∴∠CEB=∠D,
∴CE=CD.
19.解:(1)∵∠CAB=45°,∠APD=75°.
∴∠C=∠APD﹣∠CAB=30°,
∵由圆周角定理得:∠C=∠B,
∴∠B=30°;
(2)过O作OE⊥BD于E,
∵OE过O,
∴BE=DE,
∵圆心O到BD的距离为3,
∴OE=3,
∵AO=BO,DE=BE,
∴AD=2OE=6.
20.(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBO,
∴,
∴OD⊥AC;
(2)解:猜想 OD=AB.
∵,OD⊥AC,
∴AN=NC.
∵,AN=NC,
∴ON是△ABC 的中位线,
∴AB=2ON,AB∥ON.
∴∠ABM=∠NDM.
∵BM=MD,∠BMA=∠DMN,
∴△ABM≌△NDM(ASA),
∴AB=ND=2ON.
∴OD=ON+ND=AB.
21.(1)证明:∵BD为直径,
∴∠BAD=90°,
∴∠ABD+∠ADB=90°,
∵AE⊥CE,
∴∠ADE+∠EAD=90°,
∵DA平分∠BDE,
∴∠ADB=∠ADE,
∴∠ABD=∠EAD,
即∠ABO=∠EAD;
(2)解:过O点作OH⊥CD于H点,连接OA,如图,则CH=DH=CD=3,
在Rt△ODH中,OH===4,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠ODA=∠ADE,
∴∠OAD=∠ADE,
∴OA∥CE,
∴∠OAE=180°﹣∠E=90°,
∵∠OHE=∠E=∠OAE=90°,
∴四边形OAEH为矩形,
∴AE=OH=4,HE=OA=5,
∴DE=5﹣3=2,
在Rt△ADE中,AD===2.
22.证明:(1)连接AK,如图1,
∵K为弧AB的中点,
∴=,
∴=+=+,
∵∠KMB=∠A+∠AKM,
而∠A对,∠AKC对,
∴∠KTC=∠KMB;
(2)连接OC,如图2,
∵K为弧AB的中点,
∴OK⊥AB,
∴∠K+∠KMB=90°,
∵OC=OD,∠D=45°,
∴∠COD=90°,
∴∠OCK+∠ONC=90°,
而OK=OC,
∴∠K=∠OCK,
∴∠KMB=∠ONC,
∵∠KMB=∠AMN,∠ONC=∠ANM,
∴∠AMN=∠ANM,
∴AM=AN.
23.解:(1)如图1,
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.理由如下:
如图2,设∠ABE=α,∠CBF=β,
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
同课章节目录
