约分与通分练习课
图片预览






文档简介
课件18张PPT。分式的性质的应用分式约分与通分练习课学习目标1、分式基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变。
2、分式的基本性质的应用:
(1)约分; (2)通分;
3、约分后,分子与分母不再有公因式,这样的分式为最简分式。分式的性质: 分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.想一想分式的约分、通分: 1.分式的约分运算,用到了哪些知识?2.通分的关键是确定几个分式的公分母;如何确定最简公分母? 最简分式 、最简公分母:约分的基本步骤:
(1)若分子﹑分母都是单项式,则约去分子、分母的公因式;
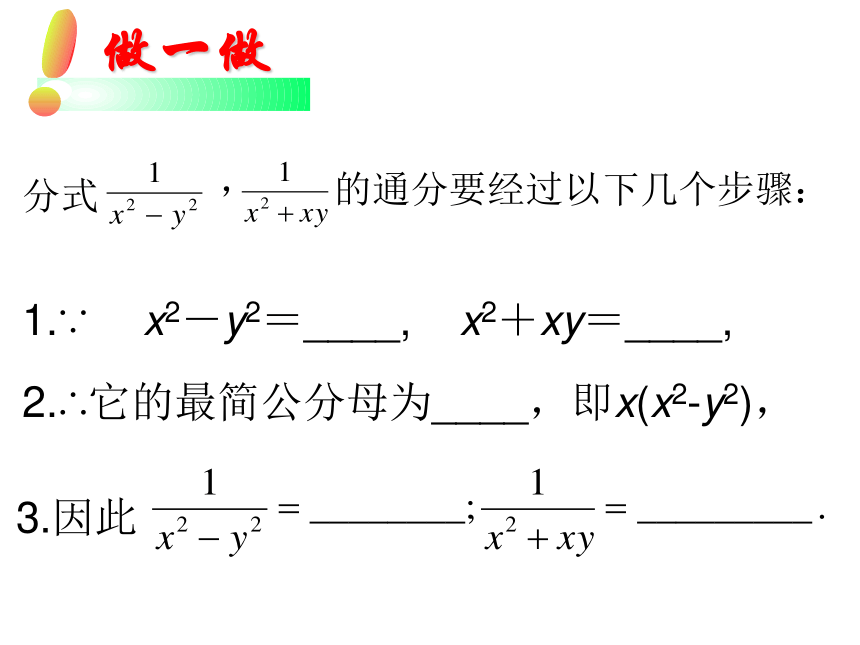
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母的公因式.约分的依据是分式的基本性质做一做1.∵ x2-y2=____, x2+xy=____, 2.∴它的最简公分母为____,即x(x2-y2), 3.因此 1、如果把分式 中的字母x,
y扩大为原来的2倍,则分式的值( )练习:A、扩大到原来2倍 B、缩小为原来的
C、不变 D、缩小为原来的2、如果把上题分式 改为 那么答案又是什么呢?( )cB1.化简下列分式: 把一个分式的分子和分母的公因式约去,这种变形称为约分,若分式的分子和分母已没有因式,则称此分式为最简分式练一练2.先约分,再求值: 解:以上解答错在哪里?化简下列分式:
(2) 应如何解答才正确呢? 像这样把一个分式的分子与分母的公因式约去,叫做分式的约分.议一议化简下列各式解: 通分:(1) (2) 注意:通分取最简公分母我们试试这个!!通分:(1),; (2),;(3).试一试试一试(2)如果把分式 中的x,y都乘以3,那么分式的值一
定( )A是原来的3倍 B.是原来的9倍 C.是原来的1/3 D.不变1.约分:(1); (2).
2.通分:(1) (2)试一试1.当分式=-1时,则x__________. 的最简公分母是_________. 有意义. 中分子、分母各项系数化成整数为______.2.分式3.当x________时, 4.不改变分式的值,把分式1 、将下列各式进行约分:2、将下列各组分别进行通分:最简公分母达标检测:
1、约分:
2、通分: 1、这节课你有哪些收获?
2、分式与分数的的区别与联系?
3、分式有意义的条件?
4、分式的基本性质?
5、分式化简的要求?学习方法指导:
分式化简的目标是“最简”,使用的方法是约分。
为实施约分必须先将分子与分母分解因式。
另外还须注意:
(1)把分子与分母降幂排列;
(2)把最高次方项的负号移到分数线左前方;
(3)把分子与分母的各项系数化为整数。总结:
2、分式的基本性质的应用:
(1)约分; (2)通分;
3、约分后,分子与分母不再有公因式,这样的分式为最简分式。分式的性质: 分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.想一想分式的约分、通分: 1.分式的约分运算,用到了哪些知识?2.通分的关键是确定几个分式的公分母;如何确定最简公分母? 最简分式 、最简公分母:约分的基本步骤:
(1)若分子﹑分母都是单项式,则约去分子、分母的公因式;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母的公因式.约分的依据是分式的基本性质做一做1.∵ x2-y2=____, x2+xy=____, 2.∴它的最简公分母为____,即x(x2-y2), 3.因此 1、如果把分式 中的字母x,
y扩大为原来的2倍,则分式的值( )练习:A、扩大到原来2倍 B、缩小为原来的
C、不变 D、缩小为原来的2、如果把上题分式 改为 那么答案又是什么呢?( )cB1.化简下列分式: 把一个分式的分子和分母的公因式约去,这种变形称为约分,若分式的分子和分母已没有因式,则称此分式为最简分式练一练2.先约分,再求值: 解:以上解答错在哪里?化简下列分式:
(2) 应如何解答才正确呢? 像这样把一个分式的分子与分母的公因式约去,叫做分式的约分.议一议化简下列各式解: 通分:(1) (2) 注意:通分取最简公分母我们试试这个!!通分:(1),; (2),;(3).试一试试一试(2)如果把分式 中的x,y都乘以3,那么分式的值一
定( )A是原来的3倍 B.是原来的9倍 C.是原来的1/3 D.不变1.约分:(1); (2).
2.通分:(1) (2)试一试1.当分式=-1时,则x__________. 的最简公分母是_________. 有意义. 中分子、分母各项系数化成整数为______.2.分式3.当x________时, 4.不改变分式的值,把分式1 、将下列各式进行约分:2、将下列各组分别进行通分:最简公分母达标检测:
1、约分:
2、通分: 1、这节课你有哪些收获?
2、分式与分数的的区别与联系?
3、分式有意义的条件?
4、分式的基本性质?
5、分式化简的要求?学习方法指导:
分式化简的目标是“最简”,使用的方法是约分。
为实施约分必须先将分子与分母分解因式。
另外还须注意:
(1)把分子与分母降幂排列;
(2)把最高次方项的负号移到分数线左前方;
(3)把分子与分母的各项系数化为整数。总结:
