江苏省江阴市要塞中学2014-2015学年初三上数学12月月考试卷及答案
文档属性
| 名称 | 江苏省江阴市要塞中学2014-2015学年初三上数学12月月考试卷及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 323.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-31 00:00:00 | ||
图片预览


文档简介
江阴市要塞中学2014~2015学年12月份检测试卷
初三数学 2014.12
说明:本试卷满分130分 考试时间:120分钟 请将本卷所有答案写在答卷上.
一、选择题:(本大题共10小题,每题3分,共30分,每题的四个选项中,只有一个符合题意)
1.若关于x的一元二次方程的常数项为0,则m的值为( ▲ )
A.1 B.0 C.1或2 D.2
2.已知等腰三角形的腰长、底边长分别是一元二次方程x2-7x+10=0的两根,则该等腰三角形的周长是 ( ▲ )
A.9或12 B.9 C.12 D.21
3.若△ABC∽△DEF,周长比为1:4.若BC=1,则EF的长是 ( ▲ )
A.2 B.4 C.8 D.16
4.抛物线的顶点坐标是 ( ▲ )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
5.在Rt△ABC中,∠C=90°,下列式子必定成立的是 ( ▲ )
A.a=c·sinB B.a=c·cosB C.a=c·tanB D.a=c·
6.如图所示,在□ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有 ( ▲ )
A.3对 B.4对 C.5对 D.6对
7.现给出以下几个命题:(1)长度相等的两条弧是等弧;(2)相等的弧所对的弦相等;(3)圆中90°的角所对的弦是直径;(4)矩形的四个顶点必在同一个圆上;(5)在同圆中,相等的弦所对的圆周角相等.其中真命题的个数为 ( ▲ )
A.1 B.2 C.3 D.4
8.半径为2的圆中,弦AB、AC的长分别2和2,则∠BAC的度数是 ( ▲ )
A.15° B.15°或45° C.15°或75° D.15°或105°
第6题图 第9题图 第10题图
9.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:
①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(,y2)是抛物线上两点,则y1>y2.其中正确的是 ( ▲ )
A.①②③ B.①③④ C.①②④ D.②③④
10.如图,A(0,8),B(0,2),点E为x轴正半轴上一动点,设tan∠AEB =m,则m的取值范围是 ( ▲ )
A.0<m≤ B.0<m≤ C.<m< D.0<m≤
二、填空题(本大题共8小题,每空2分,共16分. 不需写出解答过程,只需把答案直接填写在答题卡上相应的位置)
11.设a,b是方程的两个实数根,则ab的值为 .
12.抛物线y=2x2-bx+3的对称轴是直线x=1,则b的值为 .
13.抛物线y=-x2-6x+m,若其顶点在x轴上,则m= .
14.在Rt△ABC中,∠B=90°,AC=15,sinC=,则AB= .
15.已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 米.
16.如图,在直角三角形ABC纸片上剪出如图所示的正方体的展开图,直角三角形的两直角边与正方体展开图左下角正方形的边重合,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图中正方形的边长是 cm.
第16题图 第17题图 第18题图
17.如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2 ,BC=4,则线段DE长的最大值是 .
18.如图,一段抛物线(0≤m≤1)记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为 .
三、解答题(本大题共10小题,共计84分.解答时应写出必要的证明过程或演算步骤.)
19.(8分)计算:
(1)sin30°+cos245°+sin60°·tan45°; (2)-+(-1)0+.
20.(8分)解方程:(1)3; (2)2x-3x-1=0.
21.(6分)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长; (2)求tan∠DAE的值.
22.(9分)已知二次函数.
(1)利用配方法求出抛物线的顶点坐标;
(2)在给定的直角坐标系中,画出这个函数的图象;
(3)根据图象,写出当y<0时,x的取值范围.
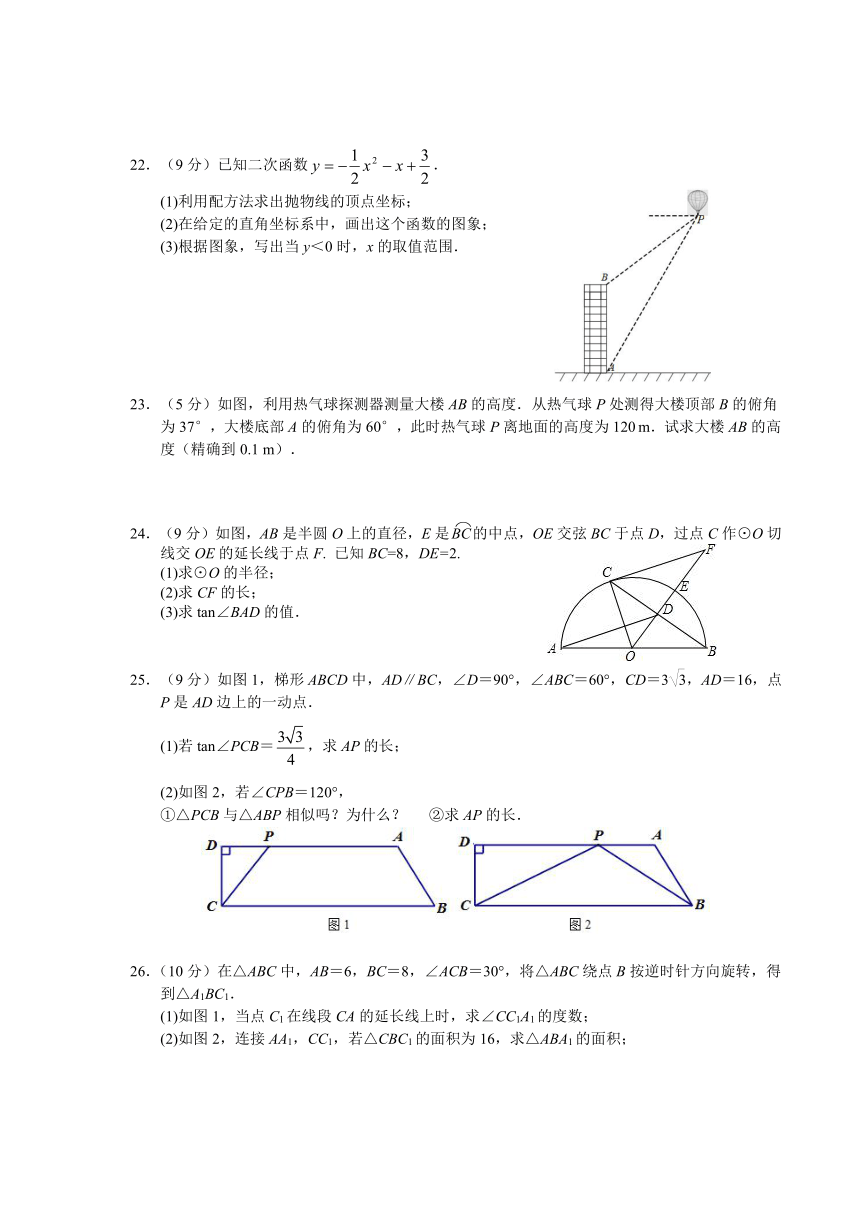
23.(5分)如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120 m.试求大楼AB的高度(精确到0.1 m).
24.(9分)如图,AB是半圆O上的直径,E是的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F. 已知BC=8,DE=2.
(1)求⊙O的半径;
(2)求CF的长;
(3)求tan∠BAD的值.
25.(9分)如图1,梯形ABCD中,AD∥BC,∠D=90°,∠ABC=60°,CD=3,AD=16,点P是AD边上的一动点.
(1)若tan∠PCB=,求AP的长;
(2)如图2,若∠CPB=120°,
①△PCB与△ABP相似吗?为什么? ②求AP的长.
26.(10分)在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1,若△CBC1的面积为16,求△ABA1的面积;
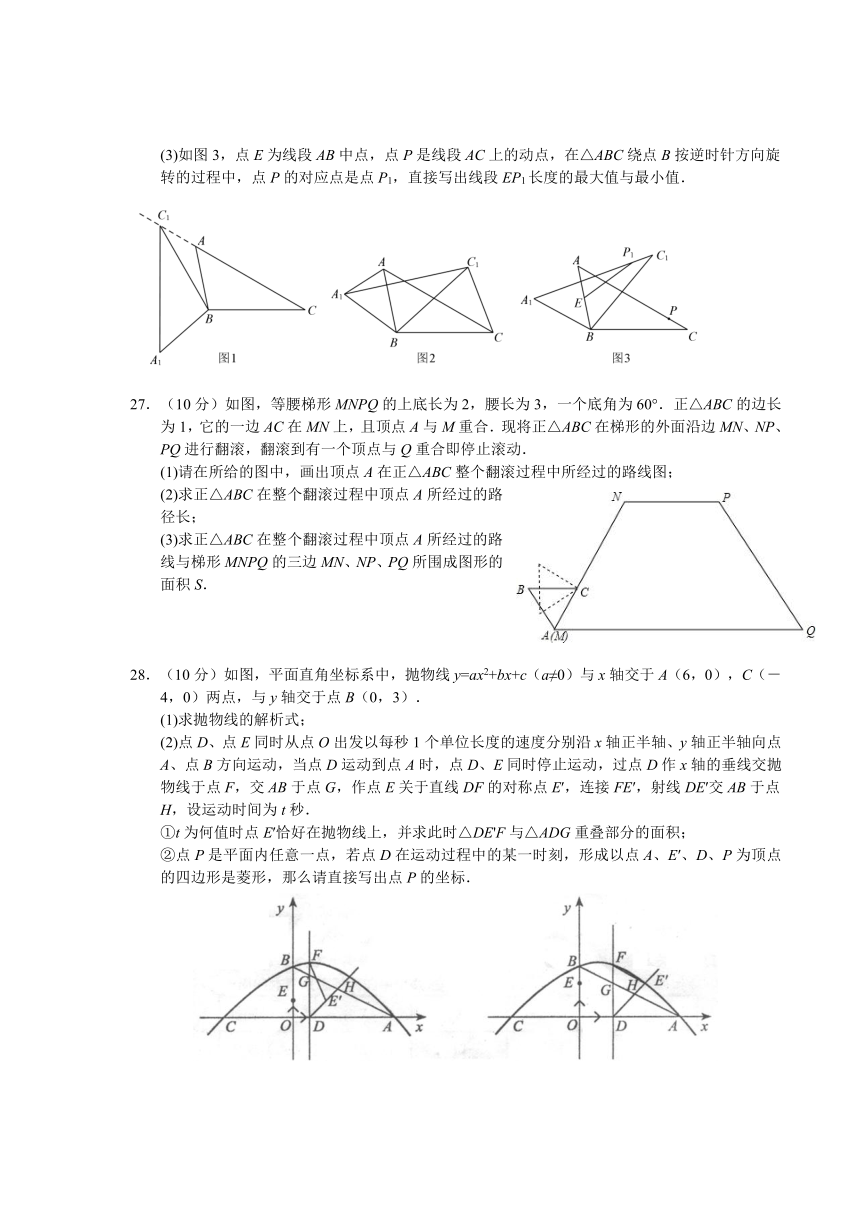
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,直接写出线段EP1长度的最大值与最小值.
27.(10分)如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正△ABC的边长为1,它的一边AC在MN上,且顶点A与M重合.现将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
(1)请在所给的图中,画出顶点A在正△ABC整个翻滚过程中所经过的路线图;
(2)求正△ABC在整个翻滚过程中顶点A所经过的路径长;
(3)求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
28.(10分)如图,平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(6,0),C(-4,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)点D、点E同时从点O出发以每秒1个单位长度的速度分别沿x轴正半轴、y轴正半轴向点A、点B方向运动,当点D运动到点A时,点D、E同时停止运动,过点D作x轴的垂线交抛物线于点F,交AB于点G,作点E关于直线DF的对称点E′,连接FE′,射线DE′交AB于点H,设运动时间为t秒.
①t为何值时点E′恰好在抛物线上,并求此时△DE'F与△ADG重叠部分的面积;
②点P是平面内任意一点,若点D在运动过程中的某一时刻,形成以点A、E′、D、P为顶点的四边形是菱形,那么请直接写出点P的坐标.
江阴市要塞中学2014~2015学年12月份检测试卷
初三数学
参考答案
一、选择题(本大题共10小题,每题3分,共30分)1-10 题 DCBBB DBDBA
二、填空题(本大题共8小题,每空2分,共16分)
11. -2014 12.4 13.-9 14.9 15.26
16.3 17.10 18.(9.5,-0.25)
三、解答题
19.(8分)
(1)1+ (2)4-
20.(8分)
(1) ,1 (2)
21.( 6分)
(1)BC=2+1( 3分),(2)tan∠DAE=( 3分).
22.(9分)(1)(-1,2) ( 4分);
(2)略( 3分);
(3)x<-3或x>1( 2分).
23.过P作PC⊥AB,垂足为C,由已知∠APC=60°,∠BPC=37°,
且由题意可知:AC=120米. ………………1分
在Rt△APC中,由tan∠APC=,
即tan60°=,得PC= EQ \F(120, )=40.………………2分
在Rt△BPC中,由tan∠BPC=,
即tan37°=,得BC=40×0.75≈51.9.………4分
因此AB =AC-BC =120-51.9=68.1,
即大楼AB的高度约为68.1米. ………………5分
24.(9分)⑴r=5 ⑵CF=⑶tan∠BAD=(各3分)
25.(9分)(1)求得PD=4 …1分
所以AP=12 …2分
(2)①相似。
理由:
∵AD∥BC,∠ABC=60°
∴∠APB=∠PBC,∠A=120°…3分
∴∠A=∠CPB=120°…4分
∴△PCB∽△ABP…5分
②过B作BE⊥DA于E
求得AE=3,BC=19…6分
设PA=x,
由△PCB∽△ABP得
…7分
则在△PBE中由勾股定理得:
…8分
解得:…9分
26.(10分)
(1)如图1,依题意得:△A1C1B≌△ACB.
∴BC1=BC,∠A1C1B =∠C=30°,………… 1分
∴∠BC1C = ∠C=30°, …………………… 2分
∴∠CC1A1 = 60°;…………………………… 3分
(2)如图2,由(1)知:△A1C1B≌△ACB,
∴A1B = AB,BC1 = BC,∠A1BC1 =∠ABC,
∴∠1 = ∠2,= = = ,…… 4分
∴ △A1BA∽△C1BC ,∴ = ()2 = ,…… 6分
∵16,∴9. ……………………………8分
(3)线段EP1长度的最大值为11,EP1长度的最小值1. …………10分
27.(10分)解:(1)如图所示:…………………(3分)
(2)点A所经过的路线长:
…………(6分)
(3)如图所示:
根据正三角形边长为1,则高AD为
故面积为:…………………(8分)
围成的图形的面积:3个圆心角为120°的扇形+2个正三角形的面积+一个半圆面积,(根据要求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S,则最后一段弧没有和PQ围成闭合的图形,故可以不求这部分面积)
所以点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S为:……………………(10分)
28.(本题满分10分)(1)依题意,得,解得
∴ 抛物线的解析式为(3分)
(2)依题意,点D、点E的坐标分别为(t,0)、(0,t)
所以点的坐标为(2t,t)
将其代入抛物线解析式整理得
解得
∵ ,∴
∴ 当时,点恰好在抛物线上(5分)
∴点D、点的坐标分别为(2,0)、(4,2)
易求直线AB的解析式为,的解析式为
联立,解得就,则点H的坐标为
点G的坐标为(2,2)
∴ 与重叠部分△DGH的面积为:。(7分)
(3)符合要求的点P有三个:、、。(10分)
C
P
A
B
初三数学 2014.12
说明:本试卷满分130分 考试时间:120分钟 请将本卷所有答案写在答卷上.
一、选择题:(本大题共10小题,每题3分,共30分,每题的四个选项中,只有一个符合题意)
1.若关于x的一元二次方程的常数项为0,则m的值为( ▲ )
A.1 B.0 C.1或2 D.2
2.已知等腰三角形的腰长、底边长分别是一元二次方程x2-7x+10=0的两根,则该等腰三角形的周长是 ( ▲ )
A.9或12 B.9 C.12 D.21
3.若△ABC∽△DEF,周长比为1:4.若BC=1,则EF的长是 ( ▲ )
A.2 B.4 C.8 D.16
4.抛物线的顶点坐标是 ( ▲ )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
5.在Rt△ABC中,∠C=90°,下列式子必定成立的是 ( ▲ )
A.a=c·sinB B.a=c·cosB C.a=c·tanB D.a=c·
6.如图所示,在□ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有 ( ▲ )
A.3对 B.4对 C.5对 D.6对
7.现给出以下几个命题:(1)长度相等的两条弧是等弧;(2)相等的弧所对的弦相等;(3)圆中90°的角所对的弦是直径;(4)矩形的四个顶点必在同一个圆上;(5)在同圆中,相等的弦所对的圆周角相等.其中真命题的个数为 ( ▲ )
A.1 B.2 C.3 D.4
8.半径为2的圆中,弦AB、AC的长分别2和2,则∠BAC的度数是 ( ▲ )
A.15° B.15°或45° C.15°或75° D.15°或105°
第6题图 第9题图 第10题图
9.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:
①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(,y2)是抛物线上两点,则y1>y2.其中正确的是 ( ▲ )
A.①②③ B.①③④ C.①②④ D.②③④
10.如图,A(0,8),B(0,2),点E为x轴正半轴上一动点,设tan∠AEB =m,则m的取值范围是 ( ▲ )
A.0<m≤ B.0<m≤ C.<m< D.0<m≤
二、填空题(本大题共8小题,每空2分,共16分. 不需写出解答过程,只需把答案直接填写在答题卡上相应的位置)
11.设a,b是方程的两个实数根,则ab的值为 .
12.抛物线y=2x2-bx+3的对称轴是直线x=1,则b的值为 .
13.抛物线y=-x2-6x+m,若其顶点在x轴上,则m= .
14.在Rt△ABC中,∠B=90°,AC=15,sinC=,则AB= .
15.已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 米.
16.如图,在直角三角形ABC纸片上剪出如图所示的正方体的展开图,直角三角形的两直角边与正方体展开图左下角正方形的边重合,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图中正方形的边长是 cm.
第16题图 第17题图 第18题图
17.如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2 ,BC=4,则线段DE长的最大值是 .
18.如图,一段抛物线(0≤m≤1)记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为 .
三、解答题(本大题共10小题,共计84分.解答时应写出必要的证明过程或演算步骤.)
19.(8分)计算:
(1)sin30°+cos245°+sin60°·tan45°; (2)-+(-1)0+.
20.(8分)解方程:(1)3; (2)2x-3x-1=0.
21.(6分)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长; (2)求tan∠DAE的值.
22.(9分)已知二次函数.
(1)利用配方法求出抛物线的顶点坐标;
(2)在给定的直角坐标系中,画出这个函数的图象;
(3)根据图象,写出当y<0时,x的取值范围.
23.(5分)如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120 m.试求大楼AB的高度(精确到0.1 m).
24.(9分)如图,AB是半圆O上的直径,E是的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F. 已知BC=8,DE=2.
(1)求⊙O的半径;
(2)求CF的长;
(3)求tan∠BAD的值.
25.(9分)如图1,梯形ABCD中,AD∥BC,∠D=90°,∠ABC=60°,CD=3,AD=16,点P是AD边上的一动点.
(1)若tan∠PCB=,求AP的长;
(2)如图2,若∠CPB=120°,
①△PCB与△ABP相似吗?为什么? ②求AP的长.
26.(10分)在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1,若△CBC1的面积为16,求△ABA1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,直接写出线段EP1长度的最大值与最小值.
27.(10分)如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正△ABC的边长为1,它的一边AC在MN上,且顶点A与M重合.现将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
(1)请在所给的图中,画出顶点A在正△ABC整个翻滚过程中所经过的路线图;
(2)求正△ABC在整个翻滚过程中顶点A所经过的路径长;
(3)求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
28.(10分)如图,平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(6,0),C(-4,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)点D、点E同时从点O出发以每秒1个单位长度的速度分别沿x轴正半轴、y轴正半轴向点A、点B方向运动,当点D运动到点A时,点D、E同时停止运动,过点D作x轴的垂线交抛物线于点F,交AB于点G,作点E关于直线DF的对称点E′,连接FE′,射线DE′交AB于点H,设运动时间为t秒.
①t为何值时点E′恰好在抛物线上,并求此时△DE'F与△ADG重叠部分的面积;
②点P是平面内任意一点,若点D在运动过程中的某一时刻,形成以点A、E′、D、P为顶点的四边形是菱形,那么请直接写出点P的坐标.
江阴市要塞中学2014~2015学年12月份检测试卷
初三数学
参考答案
一、选择题(本大题共10小题,每题3分,共30分)1-10 题 DCBBB DBDBA
二、填空题(本大题共8小题,每空2分,共16分)
11. -2014 12.4 13.-9 14.9 15.26
16.3 17.10 18.(9.5,-0.25)
三、解答题
19.(8分)
(1)1+ (2)4-
20.(8分)
(1) ,1 (2)
21.( 6分)
(1)BC=2+1( 3分),(2)tan∠DAE=( 3分).
22.(9分)(1)(-1,2) ( 4分);
(2)略( 3分);
(3)x<-3或x>1( 2分).
23.过P作PC⊥AB,垂足为C,由已知∠APC=60°,∠BPC=37°,
且由题意可知:AC=120米. ………………1分
在Rt△APC中,由tan∠APC=,
即tan60°=,得PC= EQ \F(120, )=40.………………2分
在Rt△BPC中,由tan∠BPC=,
即tan37°=,得BC=40×0.75≈51.9.………4分
因此AB =AC-BC =120-51.9=68.1,
即大楼AB的高度约为68.1米. ………………5分
24.(9分)⑴r=5 ⑵CF=⑶tan∠BAD=(各3分)
25.(9分)(1)求得PD=4 …1分
所以AP=12 …2分
(2)①相似。
理由:
∵AD∥BC,∠ABC=60°
∴∠APB=∠PBC,∠A=120°…3分
∴∠A=∠CPB=120°…4分
∴△PCB∽△ABP…5分
②过B作BE⊥DA于E
求得AE=3,BC=19…6分
设PA=x,
由△PCB∽△ABP得
…7分
则在△PBE中由勾股定理得:
…8分
解得:…9分
26.(10分)
(1)如图1,依题意得:△A1C1B≌△ACB.
∴BC1=BC,∠A1C1B =∠C=30°,………… 1分
∴∠BC1C = ∠C=30°, …………………… 2分
∴∠CC1A1 = 60°;…………………………… 3分
(2)如图2,由(1)知:△A1C1B≌△ACB,
∴A1B = AB,BC1 = BC,∠A1BC1 =∠ABC,
∴∠1 = ∠2,= = = ,…… 4分
∴ △A1BA∽△C1BC ,∴ = ()2 = ,…… 6分
∵16,∴9. ……………………………8分
(3)线段EP1长度的最大值为11,EP1长度的最小值1. …………10分
27.(10分)解:(1)如图所示:…………………(3分)
(2)点A所经过的路线长:
…………(6分)
(3)如图所示:
根据正三角形边长为1,则高AD为
故面积为:…………………(8分)
围成的图形的面积:3个圆心角为120°的扇形+2个正三角形的面积+一个半圆面积,(根据要求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S,则最后一段弧没有和PQ围成闭合的图形,故可以不求这部分面积)
所以点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S为:……………………(10分)
28.(本题满分10分)(1)依题意,得,解得
∴ 抛物线的解析式为(3分)
(2)依题意,点D、点E的坐标分别为(t,0)、(0,t)
所以点的坐标为(2t,t)
将其代入抛物线解析式整理得
解得
∵ ,∴
∴ 当时,点恰好在抛物线上(5分)
∴点D、点的坐标分别为(2,0)、(4,2)
易求直线AB的解析式为,的解析式为
联立,解得就,则点H的坐标为
点G的坐标为(2,2)
∴ 与重叠部分△DGH的面积为:。(7分)
(3)符合要求的点P有三个:、、。(10分)
C
P
A
B
同课章节目录
