2023-2024学年江苏省南通市启东市长江中学八年级(上)月考数学试卷(10月份)(无答案)
文档属性
| 名称 | 2023-2024学年江苏省南通市启东市长江中学八年级(上)月考数学试卷(10月份)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
长江中学八年级数学月考试卷
一、选择题(本题共10小题,每小题3分,共30分.)
1.下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.4,4,8 C.5,6,11 D.5,6,10
2.下列图形中具有稳定性的是( )
A.六边形 B.五边形 C.四边形 D.三角形
3.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B.
C. D.
4.如图,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )
A.100° B.90° C.80° D.70°
5.如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
A.70° B.60° C.50° D.40°
6.用尺规作已知角的平分线的理论依据是( )
A.SAS B.AAS C.SSS D.ASA
7.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
8.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A.11 B.5.5 C.7 D.3.5
9.如图,△ABC沿EF折叠使点A落在点A'处,BP、CP分别是∠ABD、∠ACD平分线,若∠P=30°,∠A'EB=20°,则∠A'FC为( )
A.125° B.130° C.135° D.140°
10..如图在△ABC,△CDE中,∠ACB=∠DCE=90°,AC=BC,CD=CE.连接BD,AE交于点F.以下四个结论:
①BD=AE;②BD⊥AE;③∠AEC+∠DBC=45°;④FC平分∠BFE,
其中结论正确的个数为( )
A.1 B.2 C.3 D.4
二、填空题(11-12题每小题3分,13-18题每题4分,共30分。)
11.如图,△ABC≌△ADE,AB=8,AC=5,BC=6,则CD= .
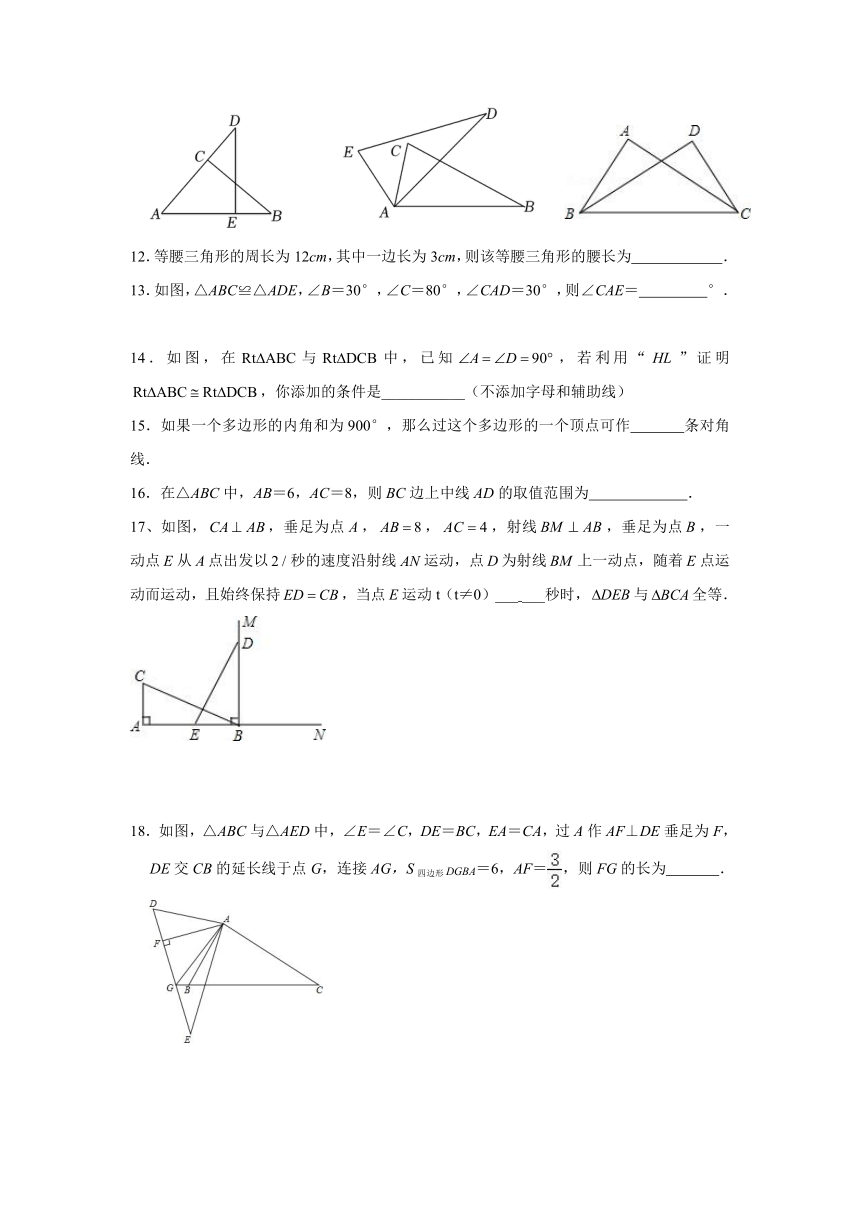
12.等腰三角形的周长为12cm,其中一边长为3cm,则该等腰三角形的腰长为 .
13.如图,△ABC≌△ADE,∠B=30°,∠C=80°,∠CAD=30°,则∠CAE= °.
14.如图,在与中,已知,若利用“”证明,你添加的条件是___________(不添加字母和辅助线)
15.如果一个多边形的内角和为900°,那么过这个多边形的一个顶点可作 条对角线.
16.在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为 .
17、如图,,垂足为点,,,射线,垂足为点,一动点从点出发以秒的速度沿射线运动,点为射线上一动点,随着点运动而运动,且始终保持,当点运动t(t≠0)___ ___秒时,与全等.
18.如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG,S四边形DGBA=6,AF=,则FG的长为 .
长江中学2023-2024学年度第一学期
八年级数学错题再练答题卷(一)
(时间:120分钟 总分:150分 )
一、选择题(本题共10小题,每小题3分,共30分.)
1 2 3 4 5 6 7 8 9 10
二、填空题(11-12题每小题3分,13-18题每题4分,共30分。)
11、 12、 13、 14、
15、 16、 17、 18、
三、解答题(共90分)
19.(10分)尺规作图(不写作法,保留作图痕迹)
已知∠AOB,(1)作∠AOB的平分线;(2)作一个角等于∠AOB.
20.(10分)如图,点B、E、C、F在同一条直线上,AB=DE,AC∥DF,AB∥DE,求证:BE=CF.
21.(10分)如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.
22.(12分)如图,已知在△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,且AE⊥BE,交BD的延长线于点E,求证:BD=2AE.
23.(12分)如图,△ABC中,三个内角的角平分线交于点O,OH⊥BC垂足为H.
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)求证:∠BOD=∠COH.
24、(12分)如图,在△ABC中,∠B=110°,延长BC至点D使CD=AB,过点C作CE∥AB且使CE=BC,连接DE并延长DE交AC于点F,交AB于点H.若∠D=20°。
(1)求证:AC=DE
(2)求∠CFE的度数.
25.(12分).已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB相交于点D,E.
(1)如图1,当CD⊥OA于D,CE⊥OB于E,则CD,CE的大小关系为 .
(2)当三角板绕点C旋转到CD与OA不垂直时,在图2这种情况下,上述结论是否还成立?若成立,请证明;若不成立,请写出你的猜想.
26.(12分)如图,已知EM是△ADE的中线,B、C是AD边上的两点,且M恰好是线段BC的中点,AE=BF,EC=FD,连接ED.
(1)求证:△AEC≌△BFD;
(2)若∠EDA+∠DBF=∠AED,AE=6,ED=8,EM=5,画出△EMD中EM边上的高DH,并求DH的长度.
一、选择题(本题共10小题,每小题3分,共30分.)
1.下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.4,4,8 C.5,6,11 D.5,6,10
2.下列图形中具有稳定性的是( )
A.六边形 B.五边形 C.四边形 D.三角形
3.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B.
C. D.
4.如图,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )
A.100° B.90° C.80° D.70°
5.如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
A.70° B.60° C.50° D.40°
6.用尺规作已知角的平分线的理论依据是( )
A.SAS B.AAS C.SSS D.ASA
7.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
8.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A.11 B.5.5 C.7 D.3.5
9.如图,△ABC沿EF折叠使点A落在点A'处,BP、CP分别是∠ABD、∠ACD平分线,若∠P=30°,∠A'EB=20°,则∠A'FC为( )
A.125° B.130° C.135° D.140°
10..如图在△ABC,△CDE中,∠ACB=∠DCE=90°,AC=BC,CD=CE.连接BD,AE交于点F.以下四个结论:
①BD=AE;②BD⊥AE;③∠AEC+∠DBC=45°;④FC平分∠BFE,
其中结论正确的个数为( )
A.1 B.2 C.3 D.4
二、填空题(11-12题每小题3分,13-18题每题4分,共30分。)
11.如图,△ABC≌△ADE,AB=8,AC=5,BC=6,则CD= .
12.等腰三角形的周长为12cm,其中一边长为3cm,则该等腰三角形的腰长为 .
13.如图,△ABC≌△ADE,∠B=30°,∠C=80°,∠CAD=30°,则∠CAE= °.
14.如图,在与中,已知,若利用“”证明,你添加的条件是___________(不添加字母和辅助线)
15.如果一个多边形的内角和为900°,那么过这个多边形的一个顶点可作 条对角线.
16.在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为 .
17、如图,,垂足为点,,,射线,垂足为点,一动点从点出发以秒的速度沿射线运动,点为射线上一动点,随着点运动而运动,且始终保持,当点运动t(t≠0)___ ___秒时,与全等.
18.如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG,S四边形DGBA=6,AF=,则FG的长为 .
长江中学2023-2024学年度第一学期
八年级数学错题再练答题卷(一)
(时间:120分钟 总分:150分 )
一、选择题(本题共10小题,每小题3分,共30分.)
1 2 3 4 5 6 7 8 9 10
二、填空题(11-12题每小题3分,13-18题每题4分,共30分。)
11、 12、 13、 14、
15、 16、 17、 18、
三、解答题(共90分)
19.(10分)尺规作图(不写作法,保留作图痕迹)
已知∠AOB,(1)作∠AOB的平分线;(2)作一个角等于∠AOB.
20.(10分)如图,点B、E、C、F在同一条直线上,AB=DE,AC∥DF,AB∥DE,求证:BE=CF.
21.(10分)如图,∠ACB=90°,BC=AC,AD⊥CE,BE⊥CE,垂足分别为D、E,AD=2.5cm,BE=0.8cm.求DE的长.
22.(12分)如图,已知在△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,且AE⊥BE,交BD的延长线于点E,求证:BD=2AE.
23.(12分)如图,△ABC中,三个内角的角平分线交于点O,OH⊥BC垂足为H.
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)求证:∠BOD=∠COH.
24、(12分)如图,在△ABC中,∠B=110°,延长BC至点D使CD=AB,过点C作CE∥AB且使CE=BC,连接DE并延长DE交AC于点F,交AB于点H.若∠D=20°。
(1)求证:AC=DE
(2)求∠CFE的度数.
25.(12分).已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB相交于点D,E.
(1)如图1,当CD⊥OA于D,CE⊥OB于E,则CD,CE的大小关系为 .
(2)当三角板绕点C旋转到CD与OA不垂直时,在图2这种情况下,上述结论是否还成立?若成立,请证明;若不成立,请写出你的猜想.
26.(12分)如图,已知EM是△ADE的中线,B、C是AD边上的两点,且M恰好是线段BC的中点,AE=BF,EC=FD,连接ED.
(1)求证:△AEC≌△BFD;
(2)若∠EDA+∠DBF=∠AED,AE=6,ED=8,EM=5,画出△EMD中EM边上的高DH,并求DH的长度.
同课章节目录
