专题2.37有理数的混合运算 直通中考(含解析)2023-2024学年七年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题2.37有理数的混合运算 直通中考(含解析)2023-2024学年七年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览



文档简介
专题2.37 有理数的混合运算(直通中考)
【要点回顾1】有理数加减乘除混合运算
(1)在运算时要注意“先乘除,后加减”的顺序进行,如有括号,应先算括号里面的,在同级运算中,要按从左到右的顺序来计算.
(2)能用运算律的要使用运算律,使用时注意只有加法和乘法有运算律,而减法和除法没有,运算律必须先统一运算再应用.
【要点回顾2】有理数的混合运算
有理数混合运算的顺序:先乘方,再乘除,最后加减;同级运算,按从左到右顺序进行;如有括号,通常先算括号里面的,按小括号、中括号和大括号依次计算.
一、单选题
(2023·浙江杭州·统考中考真题)
1.( )
A.0 B.2 C.4 D.8
(2021·四川宜宾·统考中考真题)
2.在我国远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是远古时期一位母亲记录孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是( )
A.27 B.42 C.55 D.210
(2021·陕西·统考中考真题)
3.计算:( )
A.1 B.-1 C.6 D.-6
(2021·江苏镇江·统考中考真题)
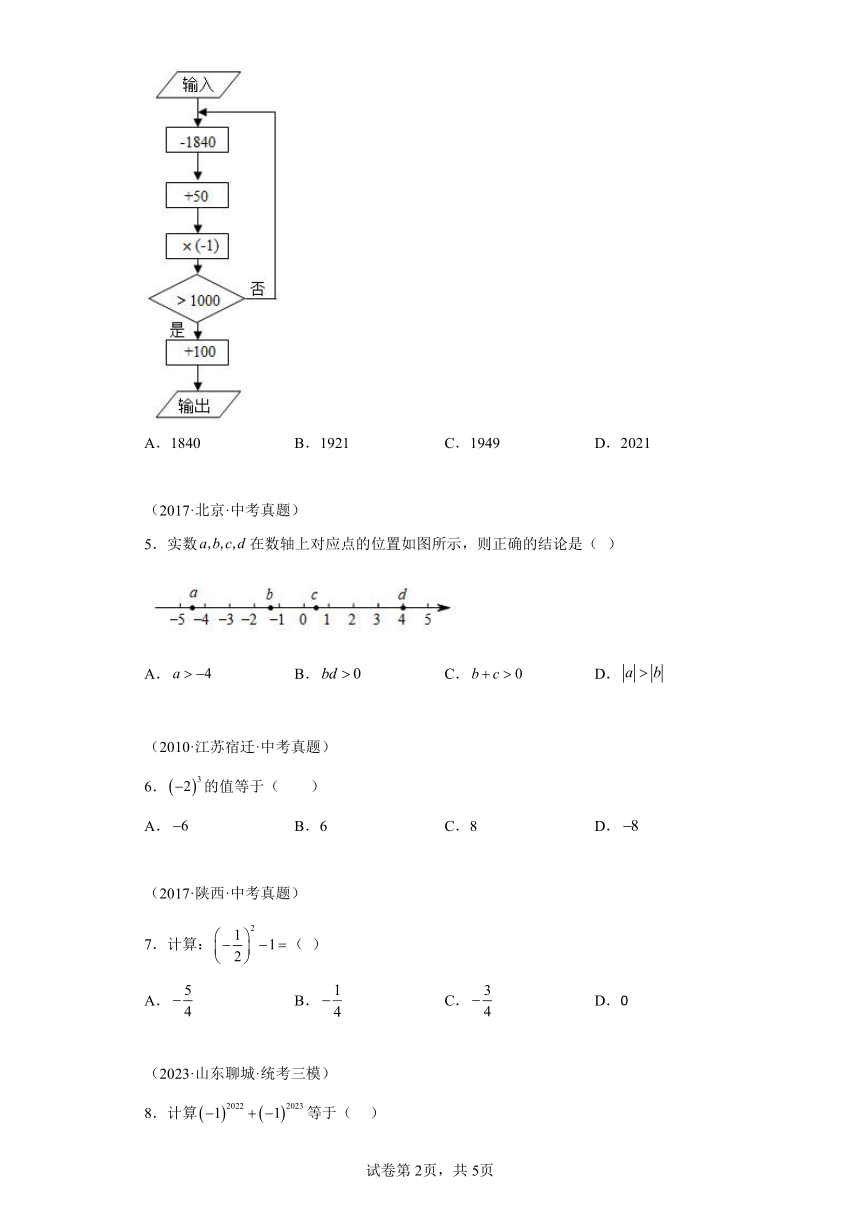
4.如图,输入数值1921,按所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),输出的结果为( )
A.1840 B.1921 C.1949 D.2021
(2017·北京·中考真题)
5.实数在数轴上对应点的位置如图所示,则正确的结论是( )
A. B. C. D.
(2010·江苏宿迁·中考真题)
6.的值等于( )
A. B.6 C.8 D.
(2017·陕西·中考真题)
7.计算:( )
A. B. C. D.0
(2023·山东聊城·统考三模)
8.计算等于( )
A.2 B.0 C. D.
(2019·广西贺州·统考中考真题)
9.计算的结果是( )
A. B. C. D.
(2023·浙江温州·校考二模)
10.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.母亲甲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子1出生后的天数,如图1所示,孩子1出生后的天数是(天),母亲乙按照母亲甲的做法记录孩子2出生后的天数,如图2所示,则孩子2出生后的天数比孩子1 出生后的天数( )
A.少41天 B.少42天 C.多41天 D.多42天
二、填空题
(2023·湖北随州·统考中考真题)
11.计算: .
(2022·四川凉山·统考中考真题)
12.计算:-12+|-2023|= .
(2021·宁夏银川·统考一模)
13.计算:(—1)2009× .
(2022·湖北宜昌·统考中考真题)
14.中国是世界上首先使用负数的国家.两千多年前战国时期李悝所著的《法经》中已出现使用负数的实例.《九章算术》的“方程”一章,在世界数学史上首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法.请计算以下涉及“负数”的式子的值: .
(2022·山东烟台·统考中考真题)
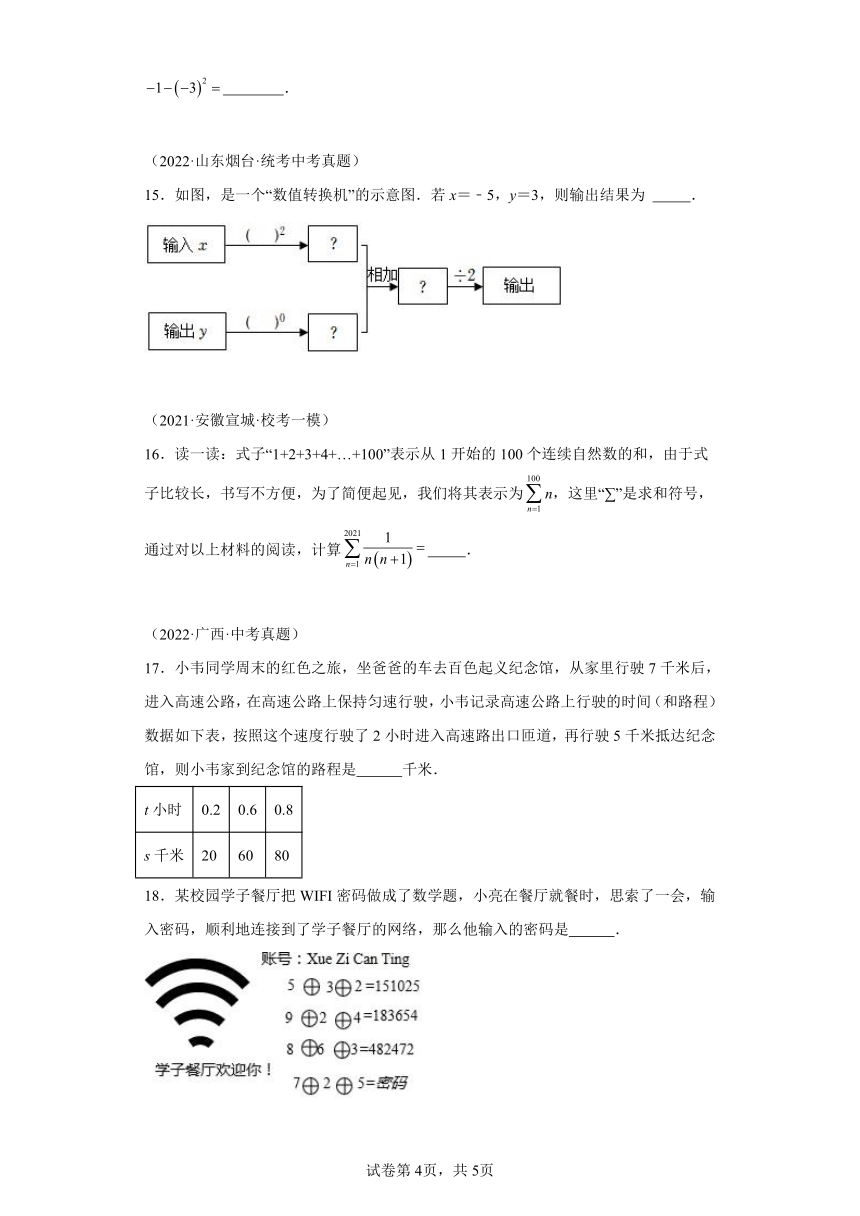
15.如图,是一个“数值转换机”的示意图.若x=﹣5,y=3,则输出结果为 .
(2021·安徽宣城·校考一模)
16.读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为n,这里“∑”是求和符号,通过对以上材料的阅读,计算 .
(2022·广西·中考真题)
17.小韦同学周末的红色之旅,坐爸爸的车去百色起义纪念馆,从家里行驶7千米后,进入高速公路,在高速公路上保持匀速行驶,小韦记录高速公路上行驶的时间(和路程)数据如下表,按照这个速度行驶了2小时进入高速路出口匝道,再行驶5千米抵达纪念馆,则小韦家到纪念馆的路程是 千米.
t小时 0.2 0.6 0.8
s千米 20 60 80
18.某校园学子餐厅把WIFI密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络,那么他输入的密码是 .
三、解答题
(2022·广西柳州·统考中考真题)
19.计算:3×(﹣1)+22+|﹣4|.
(2023·广西·统考中考真题)
20.计算:.
(2022·广西桂林·统考中考真题)
21.计算:(﹣2)×0+5.
(2022·广西·统考中考真题)
22.计算:.
(2021·广西来宾·统考中考真题)
23.计算:.
(2021·浙江台州·统考中考真题)
24.小华输液前发现瓶中药液共250毫升,输液器包装袋上标有“15滴/毫升”.输液开始时,药液流速为75滴/分钟.小华感觉身体不适,输液10分钟时调整了药液流速,输液20分钟时,瓶中的药液余量为160毫升.
(1)求输液10分钟时瓶中的药液余量;
(2)求小华从输液开始到结束所需的时间.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】先计算乘方,再计算加法即可求解.
【详解】解:,
故选:D.
【点睛】本题考查有理数度混合运算,熟练掌握有理数乘方运算法则是解题的关键.
2.B
【分析】由题可知,孩子出生的天数的五进制数为132,化为十进制数即可.
【详解】解:根据题意得:孩子出生的天数的五进制数为132,
化为十进制数为:132=1×52+3×51+2×50=42.
故选:B.
【点睛】本题主要考查了进位制,解题的关键是会将五进制转化成十进制.
3.D
【分析】根据有理数的运算法则可直接进行求解.
【详解】解:;
故选D.
【点睛】本题主要考查有理数的乘法法则,熟练掌握有理数的乘法法则是解题的关键.
4.D
【分析】把1921代入程序中计算,判断即可得到结果.
【详解】解:把1921代入得:(1921﹣1840+50)×(﹣1)=﹣131<1000,
把﹣131代入得:(﹣131﹣1840+50)×(﹣1)=1921>1000,
则输出结果为1921+100=2021.
故选:D.
【点睛】此题考查了有理数的混合运算,弄清程序中的运算过程是解本题的关键.
5.D
【分析】根据数轴上点的位置关系,可得a,b,c,d的大小,根据有理数的运算,绝对值的性质,可得答案.
【详解】解:由数轴上点的位置,得:-5A、a<-4,故A不符合题意;
B、bd<0,故B不符合题意;
C、b+c<0,故C不符合题意;
D、∵|a|>4,|b|<2,∴|a|>|b|,故D符合题意;
故选:D.
【点睛】本题考查了数轴、绝对值以及有理数的混合运算,根据数轴确定点的位置和点表示数的大小是关键.
6.D
【分析】先确定出幂的符号,再求出23的值即可.
【详解】解:是奇数,
的结果为负数.
,
.
故选D.
【点睛】解答此题的关键是熟知以下知识:一个正数的任何次幂都是正数,负数的偶次幂是正数,负数的奇次幂是负数,0的任何次幂都是0.
7.C
【分析】先计算有理数的乘方,然后计算有理数的减法,即可求解.
【详解】解:,
故选:C.
【点睛】本题考查了有理数的混合运算,熟练掌握有理数的运算法则是解题的关键.
8.B
【分析】先根据有理数乘方法则计算,再根据有理数加法法则计算即可.
【详解】解:
.
故选:B.
【点睛】本题考查有理数混合运算,熟练掌握有理数乘方法则和有理数加法法则是解题的关键.
9.B
【分析】把每个分数写成两个分数之差的一半,然后再进行简便运算.
【详解】解:原式=
=
= .
故选B.
【点睛】本题是一个规律计算题,主要考查了有理数的混合运算,关键是把分数乘法转化成分数减法来计算.
10.A
【分析】根据已知算法求出孩子2出生后的天数,相减即可得到答案.
【详解】解:由已知算法可知,孩子2出生后的天数是(天),
(天),
孩子2出生后的天数比孩子1 出生后的天数少41天,
故选A.
【点睛】本题考查了含乘方的有理数混合运算,理解题意,掌握“结绳计数”满七进一的计算方法是解题关键.
11.0
【分析】先算乘方,再计算乘法,最后算加减.
【详解】解:.
故答案为:0.
【点睛】此题主要考查了有理数的混合运算,关键是掌握运算法则.
12.2022
【分析】先计算有理数的乘方、化简绝对值,再计算加法即可得.
【详解】解:原式
,
故答案为:2022.
【点睛】本题考查了含乘方的有理数混合运算,熟练掌握有理数的运算法则是解题关键.
13.2
【分析】根据有理数的乘方、乘除法法则运算即可.
【详解】解:,
故答案为2.
【点睛】本题主要考查了有理数的乘方、有理数的乘除法运算,熟练掌握有理数的乘除法运算法则是解题的关键.
14.-10
【分析】根据有理数运算法则进行计算即可.
【详解】解:,
故答案为:.
【点睛】此题考查含乘方的有理数混合运算,掌握乘方的计算法则,有理数混合运算的计算法则是解题的关键.
15.13
【分析】根据题意可得,把,代入进行计算即可解答.
【详解】解:当,时,
.
故答案为:13.
【点睛】本题考查了有理数的混合运算,准确熟练地进行计算是解题的关键.
16.
【分析】根据求和公式写出分数的和的形式,根据分数的性质计算即可.
【详解】解:由题意得,
=1
=1
,
故答案为:.
【点睛】本题考查的是数字的变化类问题,根据题意写出分数的和的形式、并正确进行分解是解题的关键.
17.212
【分析】根据路程÷时间=速度,求出在高速公路上行驶的速度,再根据路程=速度×时间求出子高速公路行驶的路程,再和其它两段路程相加即可求解.
【详解】解:在高速公路上行驶的速度为平均每小时:20÷0.2=100(千米)
在高速公路上行驶的路程为:100×2=200(千米)
所以小韦家到纪念馆的路程是:7+200+5=212(千米).
故答案为:212
【点睛】本题主要考查了根据题意求行程的问题,解题的关键是读懂题意,弄清速度,时间,路程三者之间的关系.
18.143549
【分析】根据题中密码规律确定所求即可.
【详解】532=5×3×10000+5×2×100+5×(2+3)=151025
924=9×2×10000+9×4×100+9×(2+4)=183654,
863=8×6×10000+8×3×100+8×(3+6)=482472,
∴725=7×2×10000+7×5×100+7×(2+5)=143549.
故答案为143549
【点睛】本题考查有理数的混合运算,根据题意得出规律并熟练掌握运算法则是解题关键.
19.5
【分析】先计算乘方运算,同步计算乘法运算,化简绝对值,再合并即可.
【详解】解:原式=﹣3+4+4
=5.
【点睛】本题考查的是含乘方的有理数的混合运算,掌握“含乘方的有理数的混合运算的运算顺序”是解本题的关键.
20.6
【分析】根据有理数的混合运算法则求解即可.
【详解】
.
【点睛】本题主要考查了含乘方的有理数混合计算,熟知相关计算法则是解题的关键.
21.5
【分析】根据有理数的混合运算顺序,先计算乘法,再计算加法即可.
【详解】解:(﹣2)×0+5
=0+5
=5.
【点睛】本题考查了有理数的混合运算,掌握相关运算法则是解答本题的关键.
22.3
【分析】先计算括号内的,并计算乘方,再计算乘法,最后计算加减即可.
【详解】解:原式=1×3+4-4
=3+4-4
=3.
【点睛】本题考查有理数混合运算,熟练掌握有理数运算法则是解题的关键,注意解题时要注意运算顺序:从高级到低级运算,有括号时应先算括号里的.
23.-2
【分析】先分别计算出有理数的乘方及括号内的有理数加减,再计算乘除,即可求得结果.
【详解】解:
.
【点睛】此题考查了有理数的混合运算,熟练掌握有理数混合运算的运算顺序及相关运算法则是解答此题的关键.
24.(1)输液10分钟时瓶中的药液余量为200毫升;(2)小华从输液开始到结束所需的时间为60分钟.
【分析】(1)先求出每分钟输液多少毫升,进而即可求解;
(2)先求出输液10分钟时调整后的药液流速,进而即可求解.
【详解】(1)解:75÷15=5(毫升/分钟),
250-5×10=200(毫升),
答:输液10分钟时瓶中的药液余量为200毫升;
(2)(200-160)÷10=4(毫升/分钟),
160÷4+20=60(分钟),
答:小华从输液开始到结束所需的时间为60分钟.
【点睛】本题主要考查有理数运算的实际应用,明确时间,流速,输液量三者之间的数量关系,是解题的关键.
答案第1页,共2页
答案第1页,共2页
【要点回顾1】有理数加减乘除混合运算
(1)在运算时要注意“先乘除,后加减”的顺序进行,如有括号,应先算括号里面的,在同级运算中,要按从左到右的顺序来计算.
(2)能用运算律的要使用运算律,使用时注意只有加法和乘法有运算律,而减法和除法没有,运算律必须先统一运算再应用.
【要点回顾2】有理数的混合运算
有理数混合运算的顺序:先乘方,再乘除,最后加减;同级运算,按从左到右顺序进行;如有括号,通常先算括号里面的,按小括号、中括号和大括号依次计算.
一、单选题
(2023·浙江杭州·统考中考真题)
1.( )
A.0 B.2 C.4 D.8
(2021·四川宜宾·统考中考真题)
2.在我国远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是远古时期一位母亲记录孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是( )
A.27 B.42 C.55 D.210
(2021·陕西·统考中考真题)
3.计算:( )
A.1 B.-1 C.6 D.-6
(2021·江苏镇江·统考中考真题)
4.如图,输入数值1921,按所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),输出的结果为( )
A.1840 B.1921 C.1949 D.2021
(2017·北京·中考真题)
5.实数在数轴上对应点的位置如图所示,则正确的结论是( )
A. B. C. D.
(2010·江苏宿迁·中考真题)
6.的值等于( )
A. B.6 C.8 D.
(2017·陕西·中考真题)
7.计算:( )
A. B. C. D.0
(2023·山东聊城·统考三模)
8.计算等于( )
A.2 B.0 C. D.
(2019·广西贺州·统考中考真题)
9.计算的结果是( )
A. B. C. D.
(2023·浙江温州·校考二模)
10.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.母亲甲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子1出生后的天数,如图1所示,孩子1出生后的天数是(天),母亲乙按照母亲甲的做法记录孩子2出生后的天数,如图2所示,则孩子2出生后的天数比孩子1 出生后的天数( )
A.少41天 B.少42天 C.多41天 D.多42天
二、填空题
(2023·湖北随州·统考中考真题)
11.计算: .
(2022·四川凉山·统考中考真题)
12.计算:-12+|-2023|= .
(2021·宁夏银川·统考一模)
13.计算:(—1)2009× .
(2022·湖北宜昌·统考中考真题)
14.中国是世界上首先使用负数的国家.两千多年前战国时期李悝所著的《法经》中已出现使用负数的实例.《九章算术》的“方程”一章,在世界数学史上首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法.请计算以下涉及“负数”的式子的值: .
(2022·山东烟台·统考中考真题)
15.如图,是一个“数值转换机”的示意图.若x=﹣5,y=3,则输出结果为 .
(2021·安徽宣城·校考一模)
16.读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为n,这里“∑”是求和符号,通过对以上材料的阅读,计算 .
(2022·广西·中考真题)
17.小韦同学周末的红色之旅,坐爸爸的车去百色起义纪念馆,从家里行驶7千米后,进入高速公路,在高速公路上保持匀速行驶,小韦记录高速公路上行驶的时间(和路程)数据如下表,按照这个速度行驶了2小时进入高速路出口匝道,再行驶5千米抵达纪念馆,则小韦家到纪念馆的路程是 千米.
t小时 0.2 0.6 0.8
s千米 20 60 80
18.某校园学子餐厅把WIFI密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络,那么他输入的密码是 .
三、解答题
(2022·广西柳州·统考中考真题)
19.计算:3×(﹣1)+22+|﹣4|.
(2023·广西·统考中考真题)
20.计算:.
(2022·广西桂林·统考中考真题)
21.计算:(﹣2)×0+5.
(2022·广西·统考中考真题)
22.计算:.
(2021·广西来宾·统考中考真题)
23.计算:.
(2021·浙江台州·统考中考真题)
24.小华输液前发现瓶中药液共250毫升,输液器包装袋上标有“15滴/毫升”.输液开始时,药液流速为75滴/分钟.小华感觉身体不适,输液10分钟时调整了药液流速,输液20分钟时,瓶中的药液余量为160毫升.
(1)求输液10分钟时瓶中的药液余量;
(2)求小华从输液开始到结束所需的时间.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】先计算乘方,再计算加法即可求解.
【详解】解:,
故选:D.
【点睛】本题考查有理数度混合运算,熟练掌握有理数乘方运算法则是解题的关键.
2.B
【分析】由题可知,孩子出生的天数的五进制数为132,化为十进制数即可.
【详解】解:根据题意得:孩子出生的天数的五进制数为132,
化为十进制数为:132=1×52+3×51+2×50=42.
故选:B.
【点睛】本题主要考查了进位制,解题的关键是会将五进制转化成十进制.
3.D
【分析】根据有理数的运算法则可直接进行求解.
【详解】解:;
故选D.
【点睛】本题主要考查有理数的乘法法则,熟练掌握有理数的乘法法则是解题的关键.
4.D
【分析】把1921代入程序中计算,判断即可得到结果.
【详解】解:把1921代入得:(1921﹣1840+50)×(﹣1)=﹣131<1000,
把﹣131代入得:(﹣131﹣1840+50)×(﹣1)=1921>1000,
则输出结果为1921+100=2021.
故选:D.
【点睛】此题考查了有理数的混合运算,弄清程序中的运算过程是解本题的关键.
5.D
【分析】根据数轴上点的位置关系,可得a,b,c,d的大小,根据有理数的运算,绝对值的性质,可得答案.
【详解】解:由数轴上点的位置,得:-5
B、bd<0,故B不符合题意;
C、b+c<0,故C不符合题意;
D、∵|a|>4,|b|<2,∴|a|>|b|,故D符合题意;
故选:D.
【点睛】本题考查了数轴、绝对值以及有理数的混合运算,根据数轴确定点的位置和点表示数的大小是关键.
6.D
【分析】先确定出幂的符号,再求出23的值即可.
【详解】解:是奇数,
的结果为负数.
,
.
故选D.
【点睛】解答此题的关键是熟知以下知识:一个正数的任何次幂都是正数,负数的偶次幂是正数,负数的奇次幂是负数,0的任何次幂都是0.
7.C
【分析】先计算有理数的乘方,然后计算有理数的减法,即可求解.
【详解】解:,
故选:C.
【点睛】本题考查了有理数的混合运算,熟练掌握有理数的运算法则是解题的关键.
8.B
【分析】先根据有理数乘方法则计算,再根据有理数加法法则计算即可.
【详解】解:
.
故选:B.
【点睛】本题考查有理数混合运算,熟练掌握有理数乘方法则和有理数加法法则是解题的关键.
9.B
【分析】把每个分数写成两个分数之差的一半,然后再进行简便运算.
【详解】解:原式=
=
= .
故选B.
【点睛】本题是一个规律计算题,主要考查了有理数的混合运算,关键是把分数乘法转化成分数减法来计算.
10.A
【分析】根据已知算法求出孩子2出生后的天数,相减即可得到答案.
【详解】解:由已知算法可知,孩子2出生后的天数是(天),
(天),
孩子2出生后的天数比孩子1 出生后的天数少41天,
故选A.
【点睛】本题考查了含乘方的有理数混合运算,理解题意,掌握“结绳计数”满七进一的计算方法是解题关键.
11.0
【分析】先算乘方,再计算乘法,最后算加减.
【详解】解:.
故答案为:0.
【点睛】此题主要考查了有理数的混合运算,关键是掌握运算法则.
12.2022
【分析】先计算有理数的乘方、化简绝对值,再计算加法即可得.
【详解】解:原式
,
故答案为:2022.
【点睛】本题考查了含乘方的有理数混合运算,熟练掌握有理数的运算法则是解题关键.
13.2
【分析】根据有理数的乘方、乘除法法则运算即可.
【详解】解:,
故答案为2.
【点睛】本题主要考查了有理数的乘方、有理数的乘除法运算,熟练掌握有理数的乘除法运算法则是解题的关键.
14.-10
【分析】根据有理数运算法则进行计算即可.
【详解】解:,
故答案为:.
【点睛】此题考查含乘方的有理数混合运算,掌握乘方的计算法则,有理数混合运算的计算法则是解题的关键.
15.13
【分析】根据题意可得,把,代入进行计算即可解答.
【详解】解:当,时,
.
故答案为:13.
【点睛】本题考查了有理数的混合运算,准确熟练地进行计算是解题的关键.
16.
【分析】根据求和公式写出分数的和的形式,根据分数的性质计算即可.
【详解】解:由题意得,
=1
=1
,
故答案为:.
【点睛】本题考查的是数字的变化类问题,根据题意写出分数的和的形式、并正确进行分解是解题的关键.
17.212
【分析】根据路程÷时间=速度,求出在高速公路上行驶的速度,再根据路程=速度×时间求出子高速公路行驶的路程,再和其它两段路程相加即可求解.
【详解】解:在高速公路上行驶的速度为平均每小时:20÷0.2=100(千米)
在高速公路上行驶的路程为:100×2=200(千米)
所以小韦家到纪念馆的路程是:7+200+5=212(千米).
故答案为:212
【点睛】本题主要考查了根据题意求行程的问题,解题的关键是读懂题意,弄清速度,时间,路程三者之间的关系.
18.143549
【分析】根据题中密码规律确定所求即可.
【详解】532=5×3×10000+5×2×100+5×(2+3)=151025
924=9×2×10000+9×4×100+9×(2+4)=183654,
863=8×6×10000+8×3×100+8×(3+6)=482472,
∴725=7×2×10000+7×5×100+7×(2+5)=143549.
故答案为143549
【点睛】本题考查有理数的混合运算,根据题意得出规律并熟练掌握运算法则是解题关键.
19.5
【分析】先计算乘方运算,同步计算乘法运算,化简绝对值,再合并即可.
【详解】解:原式=﹣3+4+4
=5.
【点睛】本题考查的是含乘方的有理数的混合运算,掌握“含乘方的有理数的混合运算的运算顺序”是解本题的关键.
20.6
【分析】根据有理数的混合运算法则求解即可.
【详解】
.
【点睛】本题主要考查了含乘方的有理数混合计算,熟知相关计算法则是解题的关键.
21.5
【分析】根据有理数的混合运算顺序,先计算乘法,再计算加法即可.
【详解】解:(﹣2)×0+5
=0+5
=5.
【点睛】本题考查了有理数的混合运算,掌握相关运算法则是解答本题的关键.
22.3
【分析】先计算括号内的,并计算乘方,再计算乘法,最后计算加减即可.
【详解】解:原式=1×3+4-4
=3+4-4
=3.
【点睛】本题考查有理数混合运算,熟练掌握有理数运算法则是解题的关键,注意解题时要注意运算顺序:从高级到低级运算,有括号时应先算括号里的.
23.-2
【分析】先分别计算出有理数的乘方及括号内的有理数加减,再计算乘除,即可求得结果.
【详解】解:
.
【点睛】此题考查了有理数的混合运算,熟练掌握有理数混合运算的运算顺序及相关运算法则是解答此题的关键.
24.(1)输液10分钟时瓶中的药液余量为200毫升;(2)小华从输液开始到结束所需的时间为60分钟.
【分析】(1)先求出每分钟输液多少毫升,进而即可求解;
(2)先求出输液10分钟时调整后的药液流速,进而即可求解.
【详解】(1)解:75÷15=5(毫升/分钟),
250-5×10=200(毫升),
答:输液10分钟时瓶中的药液余量为200毫升;
(2)(200-160)÷10=4(毫升/分钟),
160÷4+20=60(分钟),
答:小华从输液开始到结束所需的时间为60分钟.
【点睛】本题主要考查有理数运算的实际应用,明确时间,流速,输液量三者之间的数量关系,是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
