专题3.6代数式 直通中考(含解析)2023-2024学年七年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题3.6代数式 直通中考(含解析)2023-2024学年七年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 375.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览




文档简介
专题3.6 代数式(直通中考)
一、单选题
(2023·河北·统考中考真题)
1.代数式的意义可以是( )
A.与x的和 B.与x的差 C.与x的积 D.与x的商
(2020·黑龙江大庆·统考中考真题)
2.若,则的值为( )
A.-5 B.5 C.1 D.-1
(2021·四川自贡·统考中考真题)
3.已知,则代数式的值是( )
A.31 B. C.41 D.
(2018·江苏常州·中考真题)
4.已知苹果每千克m元,则2千克苹果共多少元?
A.m-2 B.m+2 C. D.2m
(2023·湖南常德·统考中考真题)
5.若,则( )
A.5 B.1 C. D.0
(2023·四川巴中·统考中考真题)
6.若x满足,则代数式的值为( )
A.5 B.7 C.10 D.
(2018·山东枣庄·中考真题)
7.如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
A.3a+2b B.3a+4b C.6a+2b D.6a+4b
(2022·内蒙古包头·中考真题)
8.若a,b互为相反数,c的倒数是4,则的值为( )
A. B. C. D.16
(2022·贵州六盘水·统考中考真题)
9.已知,则的值是( )
A.4 B.8 C.16 D.12
(2022·广东广州·统考中考真题)
10.如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒……若按照这样的方法拼成的第个图形需要2022根小木棒,则的值为( )
A.252 B.253 C.336 D.337
二、填空题
(2022·广西梧州·统考中考真题)
11.若,则 .
(2022·湖南邵阳·统考中考真题)
12.已知,则 .
(2021·江苏苏州·统考中考真题)
13.若,则的值为 .
(2019·江苏常州·统考中考真题)
14.如果,那么代数式的值是 .
(2019·湖南怀化·统考中考真题)
15.当时,代数式的值等于 .
(2023·四川凉山·统考中考真题)
16.已知,则的值等于 .
(2023·山东临沂·统考中考真题)
17.观察下列式子
;
;
;
……
按照上述规律, .
(2020·贵州黔西·统考中考真题)
18.如图所示是一个运算程序的示意图,若开始输入x的值为625,则第2022次输出的结果为 .
三、解答题
(2019·黑龙江·统考中考真题)
19.已知:ab=1,b=2a-1,求代数式的值.
(2019·贵州贵阳·统考中考真题)
20.如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.
(1)用含字母a,b的代数式表示矩形中空白部分的面积;
(2)当a=3,b=2时,求矩形中空白部分的面积.
(2019·江苏盐城·统考中考真题)
21.【生活观察】甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价元千克
质量 金额
甲 千克 元
乙 千克 元
菜价元千克
质量 金额
甲 千克 ____元
乙 ____千克 元
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价总金额总质量)
【数学思考】设甲每次买质量为千克的菜,乙每次买金额为元的菜,两次的单价分别是元千克、元千克,用含有、、、的式子,分别表示出甲、乙两次买菜的均价、.比较、的大小,并说明理由.
【知识迁移】某船在相距为的甲、乙两码头间往返航行一次,在没有水流时,船的速度为所需时间为:如果水流速度为时(),船顺水航行速度为(),逆水航行速度为(),所需时间为请借鉴上面的研究经验,比较、的大小,并说明理由.
(2012·广东珠海·中考真题)
22.观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25;
② ×396=693× .
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.
(2013·浙江衢州·中考真题)
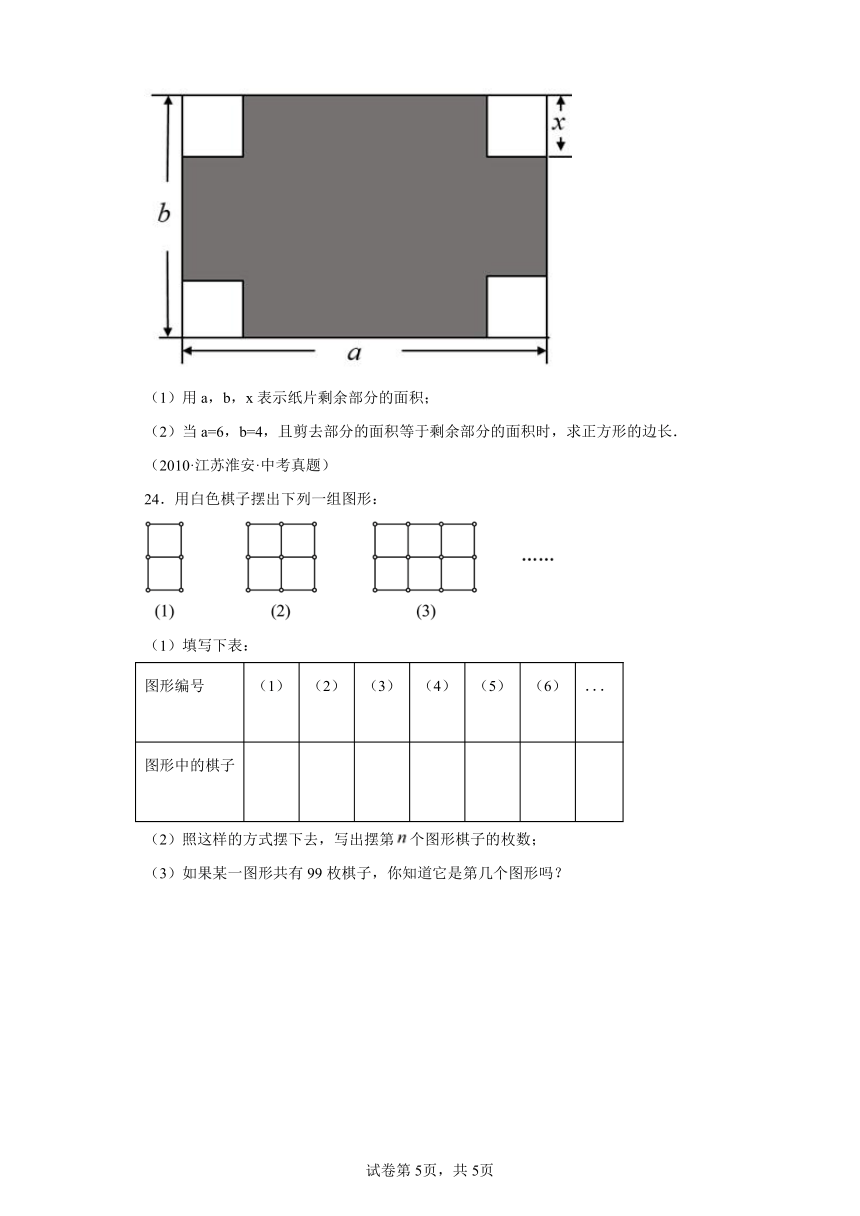
23.如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
(1)用a,b,x表示纸片剩余部分的面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
(2010·江苏淮安·中考真题)
24.用白色棋子摆出下列一组图形:
(1)填写下表:
图形编号 (1) (2) (3) (4) (5) (6) ...
图形中的棋子
(2)照这样的方式摆下去,写出摆第个图形棋子的枚数;
(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据代数式赋予实际意义即可解答.
【详解】解:的意义可以是与x的积.
故选C.
【点睛】本题主要考查了代数式的意义,掌握代数式和差乘除的意义是解答本题的关键.
2.A
【分析】根据绝对值和平方的非负性可求出x,y的值,代入计算即可;
【详解】∵,
∴,,
∴,,
∴.
故答案选A.
【点睛】本题主要考查了绝对值和平方的非负性,准确计算是解题的关键.
3.B
【分析】根据题意,可先求出x2-3x的值,再化简,然后整体代入所求代数式求值即可.
【详解】解:∵,
∴,
∴.
故选:B.
【点睛】此题考查了代数式求值,此题的关键是代数式中的字母表示的数没有明确告知,而是隐含在题设中,得出,是解题的关键.
4.D
【分析】根据单价×数量=钱数列代数式即可.
【详解】每千克m元,则2千克苹果共2m元.
故选D.
【点睛】考查了列代数式表示实际问题,解题的关键是掌握单价×数量=钱数.
5.A
【分析】把变形后整体代入求值即可.
【详解】∵,
∴
∴,
故选:A.
【点睛】本题考查代数式求值,利用整体思想是解题的关键.
6.B
【分析】由已知可得,即为,然后整体代入所求式子解答即可.
【详解】解:∵,
∴,
∴,
∴;
故选:B.
【点睛】本题考查了代数式求值,属于基础题型,熟练掌握整体代入的思想是解题关键.
7.A
【分析】根据这块矩形较长的边长=边长为3a的正方形的边长-边长为2b的小正方形的边长+边长为2b的小正方形的边长的2倍代入数据即可.
【详解】依题意有:3a﹣2b+2b×2=3a﹣2b+4b=3a+2b.
故这块矩形较长的边长为3a+2b.故选A.
【点睛】本题主要考查矩形、正方形和整式的运算,熟读题目,理解题意,清楚题中的等量关系是解答本题的关键.
8.C
【分析】根据a,b互为相反数,可得,c的倒数是4,可得 ,代入即可求解.
【详解】∵a,b互为相反数,
∴,
∵c的倒数是4,
∴,
∴,
故选:C
【点睛】本题考查了代数式的求值问题,利用已知求得,是解题的关键.
9.C
【分析】令,代入已知等式进行计算即可得.
【详解】解:观察所求式子与已知等式的关系,令,
则,
故选:C.
【点睛】本题考查了代数式求值,观察得出所求式子与已知等式的关系是解题关键.
10.B
【分析】根据图形的变化及数值的变化找出变化规律,即可得出结论.
【详解】解:设第n个图形需要an(n为正整数)根小木棒,
观察发现规律:第一个图形需要小木棒:6=6×1+0,
第二个图形需要小木棒:14=6×2+2;
第三个图形需要小木棒:22=6×3+4,…,
∴第n个图形需要小木棒:6n+2(n-1)=8n-2.
∴8n-2=2022,得:n=253,
故选:B.
【点睛】本题考查了规律型中图形的变化类,解决该题型题目时,根据给定图形中的数据找出变化规律是关键.
11.1
【分析】将代入代数式求解即可.
【详解】解:∵,
∴,
故答案为:.
【点睛】本题考查了代数式求值.解题的关键在于正确的计算.
12.2
【分析】将变形为即可计算出答案.
【详解】
∵
∴
故答案为:2.
【点睛】本题考查代数式的性质,解题的关键是熟练掌握代数式的相关知识.
13.3
【分析】根据,将式子进行变形,然后代入求出值即可.
【详解】∵ ,
∴=3m(m+2n)+6n=3m+6n=3(m+2n)=3.
故答案为:3.
【点睛】本题考查了代数式的求值,解题的关键是利用已知代数式求值.
14.
【分析】将所求式子化简后再将已知条件中整体代入即可求值;
【详解】,
,
;
故答案为.
【点睛】本题考查代数式求值;熟练掌握整体代入法求代数式的值是解题的关键.
15.-5
【分析】把a、b的值代入代数式,即可求出答案即可.
【详解】当时, ,
故答案为.
【点睛】本题考查了求代数式的值的应用,能正确进行有理数的混合运算是解此题的关键.
16.2023
【分析】把化为:代入降次,再把代入求值即可.
【详解】解:由得:,,
,
故答案为:.
【点睛】本题考查的是代数式的求值,找到整体进行降次是解题的关键.
17.
【分析】根据已有的式子,抽象出相应的数字规律,进行作答即可.
【详解】解:∵;
;
;
……
∴,
∴.
故答案为:
【点睛】本题考查数字类规律探究.解题的关键是从已有的式子中抽象出相应的数字规律.
18.1
【分析】按照程序的流程进行计算并找到规律即可.
【详解】当x=625时,,
当x=125时,,
当x=25时,,
当x=5时, ,
当x=1时, ,
当x=5时, ,
…
依此类推,以5,1循环,而(2022-2)÷2=1010,能够整除,所以输出的结果是1
故答案为:1
【点睛】本题考查了求代数式的值,根据程序框图的条件计算出前面几个值的情况,找到规律,体现了由特殊到一般的思想.
19.-1.
【分析】根据ab=1,b=2a-1,可以求得b-2a的值,从而可以求得所求式子的值.
【详解】∵ab=1,b=2a-1,∴b-2a=-1,∴
【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
20.(1)S=ab﹣a﹣b+1;(2)矩形中空白部分的面积为2;
【分析】(1)空白区域面积=矩形面积-两个阴影平行四边形面积+中间重叠平行四边形面积;
(2)将a=3,b=2代入(1)中即可;
【详解】(1)S=ab﹣a﹣b+1;
(2)当a=3,b=2时,S=6﹣3﹣2+1=2;
【点睛】本题考查阴影部分面积,平行四边形面积,代数式求值;能够准确求出阴影部分面积是解题的关键.
21.【生活观察】:(1)见解析表;(2)甲两次买菜的均价是元千克:乙两次买菜的均价是元千克;【数学思考】:当时,,当时,,见解析;【知识迁移】:,见解析.
【分析】(1)根据单价、质量与金额的关系,进行求解.(2)根据均价总金额总质量,进行求解.【数学思考】:根据均价总金额总质量,进行表示与大小比较.【知识迁移】:根据时间=路程速度,进行表示与大小比较.
【详解】(1)根据单价、质量与金额的关系,可得甲的金额和乙的质量,如图表所示
第二次:
菜价元千克
质量 金额
甲 千克 元
乙 千克 元
(2)根据均价总金额总质量,甲两次买菜的均价为元千克,乙两次买菜的均价为元千克.
【数学思考】:
,
,
.
当时,,当时,.
【知识迁移】:
,,
;
,,
,.
又,,
.
【点睛】本题考查“单价=金额质量”,“时间=路程速度”公式的综合应用,以及代数式的值的大小判别.
22.解:(1)①275;572.
②63;36.
(2)“数字对称等式”一般规律的式子为:
(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a),
证明见解析.
【分析】根据题意可得三位数中间的数等于两数的和,根据这一规律然后进行填空,从而得出答案;根据题意得出一般性的规律,然后根据多项式的计算法则进行说明理由.
【详解】(1)两位数的个位数字、十位数字、个位数与十位数之和分别是三位数的百位上的数、个位上的数、十位上的数,
∴①52×275=572×25;
②63×396=693×36;
(2)“数字对称等式”一般规律的式子为:
(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).
证明如下:
∵左边两位数的十位数字为a,个位数字为b,
∴左边的两位数是10a+b,三位数是100b+10(a+b)+a,
右边的两位数是10b+a,三位数是100a+10(a+b)+b,
∴左边=(10a+b)×[100b+10(a+b)+a]=(10a+b)(100b+10a+10b+a)
=(10a+b)(110b+11a)=11(10a+b)(10b+a),
右边=[100a+10(a+b)+b]×(10b+a)=(100a+10a+10b+b)(10b+a)
=(110a+11b)(10b+a)=11(10a+b)(10b+a),
∴左边=右边.
∴“数字对称等式”一般规律的式子为:
(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).
【点睛】考点:规律题
23.(1)ab﹣4x2(2)
【分析】(1)边长为x的正方形面积为x2,矩形面积减去4个小正方形的面积即可.
(2)依据剪去部分的面积等于剩余部分的面积,列方程求出x的值即可.
【详解】解:(1)ab﹣4x2.
(2)依题意有:,将a=6,b=4,代入上式,得x2=3.
解得x1=,x2=(舍去).
∴正方形的边长为.
24.(1)见详解;(2)3(n+1);(3)99枚.
【分析】解题注意根据图形发现规律,并用字母表示.然后根据条件代入计算.
【详解】解:(1)
图形编号 1 2 3 4 5 6
图形中的棋子 6 9 12 15 18 21
(2)第n个图形棋子的枚数是6+3(n-1)=3n+3个.
(3)设图形有99枚棋子,它是第x个图形.
根据题意得:3+3x=99
解得x=32
所以它是第32个图形.
故答案为(1)6,9,12,15,18,21.
【点睛】此题考查规律问题,观察图形,发现(1)中是6个棋子.后边多一个图形,多3个棋子.根据这一规律即可解决下列问题.
答案第1页,共2页
答案第1页,共2页
一、单选题
(2023·河北·统考中考真题)
1.代数式的意义可以是( )
A.与x的和 B.与x的差 C.与x的积 D.与x的商
(2020·黑龙江大庆·统考中考真题)
2.若,则的值为( )
A.-5 B.5 C.1 D.-1
(2021·四川自贡·统考中考真题)
3.已知,则代数式的值是( )
A.31 B. C.41 D.
(2018·江苏常州·中考真题)
4.已知苹果每千克m元,则2千克苹果共多少元?
A.m-2 B.m+2 C. D.2m
(2023·湖南常德·统考中考真题)
5.若,则( )
A.5 B.1 C. D.0
(2023·四川巴中·统考中考真题)
6.若x满足,则代数式的值为( )
A.5 B.7 C.10 D.
(2018·山东枣庄·中考真题)
7.如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
A.3a+2b B.3a+4b C.6a+2b D.6a+4b
(2022·内蒙古包头·中考真题)
8.若a,b互为相反数,c的倒数是4,则的值为( )
A. B. C. D.16
(2022·贵州六盘水·统考中考真题)
9.已知,则的值是( )
A.4 B.8 C.16 D.12
(2022·广东广州·统考中考真题)
10.如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒……若按照这样的方法拼成的第个图形需要2022根小木棒,则的值为( )
A.252 B.253 C.336 D.337
二、填空题
(2022·广西梧州·统考中考真题)
11.若,则 .
(2022·湖南邵阳·统考中考真题)
12.已知,则 .
(2021·江苏苏州·统考中考真题)
13.若,则的值为 .
(2019·江苏常州·统考中考真题)
14.如果,那么代数式的值是 .
(2019·湖南怀化·统考中考真题)
15.当时,代数式的值等于 .
(2023·四川凉山·统考中考真题)
16.已知,则的值等于 .
(2023·山东临沂·统考中考真题)
17.观察下列式子
;
;
;
……
按照上述规律, .
(2020·贵州黔西·统考中考真题)
18.如图所示是一个运算程序的示意图,若开始输入x的值为625,则第2022次输出的结果为 .
三、解答题
(2019·黑龙江·统考中考真题)
19.已知:ab=1,b=2a-1,求代数式的值.
(2019·贵州贵阳·统考中考真题)
20.如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.
(1)用含字母a,b的代数式表示矩形中空白部分的面积;
(2)当a=3,b=2时,求矩形中空白部分的面积.
(2019·江苏盐城·统考中考真题)
21.【生活观察】甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价元千克
质量 金额
甲 千克 元
乙 千克 元
菜价元千克
质量 金额
甲 千克 ____元
乙 ____千克 元
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价总金额总质量)
【数学思考】设甲每次买质量为千克的菜,乙每次买金额为元的菜,两次的单价分别是元千克、元千克,用含有、、、的式子,分别表示出甲、乙两次买菜的均价、.比较、的大小,并说明理由.
【知识迁移】某船在相距为的甲、乙两码头间往返航行一次,在没有水流时,船的速度为所需时间为:如果水流速度为时(),船顺水航行速度为(),逆水航行速度为(),所需时间为请借鉴上面的研究经验,比较、的大小,并说明理由.
(2012·广东珠海·中考真题)
22.观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25;
② ×396=693× .
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.
(2013·浙江衢州·中考真题)
23.如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
(1)用a,b,x表示纸片剩余部分的面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
(2010·江苏淮安·中考真题)
24.用白色棋子摆出下列一组图形:
(1)填写下表:
图形编号 (1) (2) (3) (4) (5) (6) ...
图形中的棋子
(2)照这样的方式摆下去,写出摆第个图形棋子的枚数;
(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据代数式赋予实际意义即可解答.
【详解】解:的意义可以是与x的积.
故选C.
【点睛】本题主要考查了代数式的意义,掌握代数式和差乘除的意义是解答本题的关键.
2.A
【分析】根据绝对值和平方的非负性可求出x,y的值,代入计算即可;
【详解】∵,
∴,,
∴,,
∴.
故答案选A.
【点睛】本题主要考查了绝对值和平方的非负性,准确计算是解题的关键.
3.B
【分析】根据题意,可先求出x2-3x的值,再化简,然后整体代入所求代数式求值即可.
【详解】解:∵,
∴,
∴.
故选:B.
【点睛】此题考查了代数式求值,此题的关键是代数式中的字母表示的数没有明确告知,而是隐含在题设中,得出,是解题的关键.
4.D
【分析】根据单价×数量=钱数列代数式即可.
【详解】每千克m元,则2千克苹果共2m元.
故选D.
【点睛】考查了列代数式表示实际问题,解题的关键是掌握单价×数量=钱数.
5.A
【分析】把变形后整体代入求值即可.
【详解】∵,
∴
∴,
故选:A.
【点睛】本题考查代数式求值,利用整体思想是解题的关键.
6.B
【分析】由已知可得,即为,然后整体代入所求式子解答即可.
【详解】解:∵,
∴,
∴,
∴;
故选:B.
【点睛】本题考查了代数式求值,属于基础题型,熟练掌握整体代入的思想是解题关键.
7.A
【分析】根据这块矩形较长的边长=边长为3a的正方形的边长-边长为2b的小正方形的边长+边长为2b的小正方形的边长的2倍代入数据即可.
【详解】依题意有:3a﹣2b+2b×2=3a﹣2b+4b=3a+2b.
故这块矩形较长的边长为3a+2b.故选A.
【点睛】本题主要考查矩形、正方形和整式的运算,熟读题目,理解题意,清楚题中的等量关系是解答本题的关键.
8.C
【分析】根据a,b互为相反数,可得,c的倒数是4,可得 ,代入即可求解.
【详解】∵a,b互为相反数,
∴,
∵c的倒数是4,
∴,
∴,
故选:C
【点睛】本题考查了代数式的求值问题,利用已知求得,是解题的关键.
9.C
【分析】令,代入已知等式进行计算即可得.
【详解】解:观察所求式子与已知等式的关系,令,
则,
故选:C.
【点睛】本题考查了代数式求值,观察得出所求式子与已知等式的关系是解题关键.
10.B
【分析】根据图形的变化及数值的变化找出变化规律,即可得出结论.
【详解】解:设第n个图形需要an(n为正整数)根小木棒,
观察发现规律:第一个图形需要小木棒:6=6×1+0,
第二个图形需要小木棒:14=6×2+2;
第三个图形需要小木棒:22=6×3+4,…,
∴第n个图形需要小木棒:6n+2(n-1)=8n-2.
∴8n-2=2022,得:n=253,
故选:B.
【点睛】本题考查了规律型中图形的变化类,解决该题型题目时,根据给定图形中的数据找出变化规律是关键.
11.1
【分析】将代入代数式求解即可.
【详解】解:∵,
∴,
故答案为:.
【点睛】本题考查了代数式求值.解题的关键在于正确的计算.
12.2
【分析】将变形为即可计算出答案.
【详解】
∵
∴
故答案为:2.
【点睛】本题考查代数式的性质,解题的关键是熟练掌握代数式的相关知识.
13.3
【分析】根据,将式子进行变形,然后代入求出值即可.
【详解】∵ ,
∴=3m(m+2n)+6n=3m+6n=3(m+2n)=3.
故答案为:3.
【点睛】本题考查了代数式的求值,解题的关键是利用已知代数式求值.
14.
【分析】将所求式子化简后再将已知条件中整体代入即可求值;
【详解】,
,
;
故答案为.
【点睛】本题考查代数式求值;熟练掌握整体代入法求代数式的值是解题的关键.
15.-5
【分析】把a、b的值代入代数式,即可求出答案即可.
【详解】当时, ,
故答案为.
【点睛】本题考查了求代数式的值的应用,能正确进行有理数的混合运算是解此题的关键.
16.2023
【分析】把化为:代入降次,再把代入求值即可.
【详解】解:由得:,,
,
故答案为:.
【点睛】本题考查的是代数式的求值,找到整体进行降次是解题的关键.
17.
【分析】根据已有的式子,抽象出相应的数字规律,进行作答即可.
【详解】解:∵;
;
;
……
∴,
∴.
故答案为:
【点睛】本题考查数字类规律探究.解题的关键是从已有的式子中抽象出相应的数字规律.
18.1
【分析】按照程序的流程进行计算并找到规律即可.
【详解】当x=625时,,
当x=125时,,
当x=25时,,
当x=5时, ,
当x=1时, ,
当x=5时, ,
…
依此类推,以5,1循环,而(2022-2)÷2=1010,能够整除,所以输出的结果是1
故答案为:1
【点睛】本题考查了求代数式的值,根据程序框图的条件计算出前面几个值的情况,找到规律,体现了由特殊到一般的思想.
19.-1.
【分析】根据ab=1,b=2a-1,可以求得b-2a的值,从而可以求得所求式子的值.
【详解】∵ab=1,b=2a-1,∴b-2a=-1,∴
【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.
20.(1)S=ab﹣a﹣b+1;(2)矩形中空白部分的面积为2;
【分析】(1)空白区域面积=矩形面积-两个阴影平行四边形面积+中间重叠平行四边形面积;
(2)将a=3,b=2代入(1)中即可;
【详解】(1)S=ab﹣a﹣b+1;
(2)当a=3,b=2时,S=6﹣3﹣2+1=2;
【点睛】本题考查阴影部分面积,平行四边形面积,代数式求值;能够准确求出阴影部分面积是解题的关键.
21.【生活观察】:(1)见解析表;(2)甲两次买菜的均价是元千克:乙两次买菜的均价是元千克;【数学思考】:当时,,当时,,见解析;【知识迁移】:,见解析.
【分析】(1)根据单价、质量与金额的关系,进行求解.(2)根据均价总金额总质量,进行求解.【数学思考】:根据均价总金额总质量,进行表示与大小比较.【知识迁移】:根据时间=路程速度,进行表示与大小比较.
【详解】(1)根据单价、质量与金额的关系,可得甲的金额和乙的质量,如图表所示
第二次:
菜价元千克
质量 金额
甲 千克 元
乙 千克 元
(2)根据均价总金额总质量,甲两次买菜的均价为元千克,乙两次买菜的均价为元千克.
【数学思考】:
,
,
.
当时,,当时,.
【知识迁移】:
,,
;
,,
,.
又,,
.
【点睛】本题考查“单价=金额质量”,“时间=路程速度”公式的综合应用,以及代数式的值的大小判别.
22.解:(1)①275;572.
②63;36.
(2)“数字对称等式”一般规律的式子为:
(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a),
证明见解析.
【分析】根据题意可得三位数中间的数等于两数的和,根据这一规律然后进行填空,从而得出答案;根据题意得出一般性的规律,然后根据多项式的计算法则进行说明理由.
【详解】(1)两位数的个位数字、十位数字、个位数与十位数之和分别是三位数的百位上的数、个位上的数、十位上的数,
∴①52×275=572×25;
②63×396=693×36;
(2)“数字对称等式”一般规律的式子为:
(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).
证明如下:
∵左边两位数的十位数字为a,个位数字为b,
∴左边的两位数是10a+b,三位数是100b+10(a+b)+a,
右边的两位数是10b+a,三位数是100a+10(a+b)+b,
∴左边=(10a+b)×[100b+10(a+b)+a]=(10a+b)(100b+10a+10b+a)
=(10a+b)(110b+11a)=11(10a+b)(10b+a),
右边=[100a+10(a+b)+b]×(10b+a)=(100a+10a+10b+b)(10b+a)
=(110a+11b)(10b+a)=11(10a+b)(10b+a),
∴左边=右边.
∴“数字对称等式”一般规律的式子为:
(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).
【点睛】考点:规律题
23.(1)ab﹣4x2(2)
【分析】(1)边长为x的正方形面积为x2,矩形面积减去4个小正方形的面积即可.
(2)依据剪去部分的面积等于剩余部分的面积,列方程求出x的值即可.
【详解】解:(1)ab﹣4x2.
(2)依题意有:,将a=6,b=4,代入上式,得x2=3.
解得x1=,x2=(舍去).
∴正方形的边长为.
24.(1)见详解;(2)3(n+1);(3)99枚.
【分析】解题注意根据图形发现规律,并用字母表示.然后根据条件代入计算.
【详解】解:(1)
图形编号 1 2 3 4 5 6
图形中的棋子 6 9 12 15 18 21
(2)第n个图形棋子的枚数是6+3(n-1)=3n+3个.
(3)设图形有99枚棋子,它是第x个图形.
根据题意得:3+3x=99
解得x=32
所以它是第32个图形.
故答案为(1)6,9,12,15,18,21.
【点睛】此题考查规律问题,观察图形,发现(1)中是6个棋子.后边多一个图形,多3个棋子.根据这一规律即可解决下列问题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
