专题3.2用字母表示数 分层练习(含解析)2023-2024学年七年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题3.2用字母表示数 分层练习(含解析)2023-2024学年七年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览




文档简介
专题3.2 用字母表示数(分层练习)
一、单选题
1.用代数式表示“与的和的平方”,正确的是( )
A. B. C. D.
2.某商店经销一种品牌的空气炸锅,其中某一型号的空气炸锅的进价为每台元,商店将进价提高30%后作为零售价销售,一段时间后,商店又按零售价的8折销售,这时该型号空气炸锅的零售价为( )
A.元 B.元 C.元 D.元
3.下列各式中,符合代数式书写规则的是( )
A. B. C. D.
4.小明在电脑上1分钟录入汉字50个,小明的爸爸1分钟录入汉字30个.如果小明和爸爸各录入个汉字,那么爸爸比小明多用( )分钟.
A. B. C. D.
5.甲,乙两商场以相同的价格出售同样的商品,当购物金额超出一定数额后,各自推出不同的优惠方案,若在两个商场购买元的商品,在甲商场需付费元,在乙商场需付费元,下列关于两个商场优惠方案的说法正确的是( )
A.购买金额不超过100元时,两个商场都不优惠
B.购买金额超过50元时,两个商场都有优惠
C.购买金额超过100元时,甲商场按收费,乙商场按收费
D.购买金额超过100元时,超出100元的部分,甲商场按收费,乙商场按收费
6.下面语句中,正确的是( )
A.比一个数大5,则这个数是 B.表示、、的积的代数式为
C.,两数的倒数和为 D.与的平方差是
7.一个长方形的长是宽的4倍多2厘米,设长为厘米,那么宽为( )
A.厘米 B.厘米 C.厘米 D.厘米
8.今年,我校成功举办了“经典诵读”比赛,其中参加比赛的男同学有人,女同学人数比男同学人数的少24人,则参加“经典诵读”比赛的学生一共有( )
A.人 B.人 C.人 D.人
9.受今年高温天气的影响,我市某企业今年月份产值为万元,月份比月份减少了,月份比月份增加了,则月份的产值为( )
A.万元 B.万元
C.万元 D.万元
10.粗心的小倩在放学回家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回家(取书时间忽略不计).已知跑步速度为x,步行速度为y,则她往返一趟的平均速度是( )
A.x B.y C. D.
11.因H7N9禽流感致病性强,某药房打算让利于民,板蓝根一箱原价为100元,现有下列四种调价方案,其中0<n<m<100,则调价后板蓝根价格最低的方案是( )
A.先涨价m%,再降价n% B.先涨价n%,再降价m%
C.先涨价,再降价再降价 D.无法确定
12.如图,在图1中,、、分别是等边 的边、、的中点,在图2中,,,分别是的边、、的中点,…,按此规律,则第n个图形中菱形的个数共有( )个.
A. B. C. D.
13.观察算式,探究规律:
当时,;
当时, ;
当时,;
当时,;…
那么与n的关系为( )
A. B. C. D.
14.已知,,,,若,都是正整数符合前面式子的规律,则的值是( )
A.17 B.18 C.19 D.20
15.观察下列一组图形,其中图中共有个小黑点,图中共有个小黑点,图中共有个小黑点,,按此规律,图中小黑点的个数是( )
A.46 B.51 C.61 D.76
二、填空题
16.书写单项式的注意事项:
①数字要写在字母的 ;
②数字与字母相乘,字母与字母相乘时,“×”号可以省略或用 替代;
③系数是带分数时要写成 .
17.如图是小明同学设计的一个运算程序的流程图,输入一个有理数x,便可输出一个相应的有理数y,写出y与x之间的关系式: .
18.苹果原价是每千克x元,按9折优惠出售,该苹果现价是每千克 元.(用含x的代数式表示)
19.从甲地到乙地有两条都是3千米的路,其中第一条是平路,第二条是1千米的上坡路,2千米的下坡路:小明在上坡路上的骑车速度为千米/时,在平路上的骑车速度为千米/时,在下坡路上的骑车速度为千米/时,则他走第二条路比走第一条路多用了 小时.(用含的代数式表示)
20.如图所示是2004年10月份的日历.现在日历中任意框出4个数,请用一个等式表示,,,之间的关系: .
21.一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是 .
22.某校初一(1)班有m人参加晚托课后服务,其中有参加足球兴趣活动,有8人参加书法兴趣活动,则参加其余兴趣活动的共 人.
23.小红的房间窗户的装饰物如图所示,由两个四分之一圆组成(半径分别相同),窗户中能射进阳光的部分的面积是 .
24.如图,长方形中,,,M、N两点分别从点A、C同时出发,沿长方形的边相向而行,速度都是秒,设他们的运动时间为t秒,当M、N两点第一次相遇时, 秒;第十次相遇时, 秒.
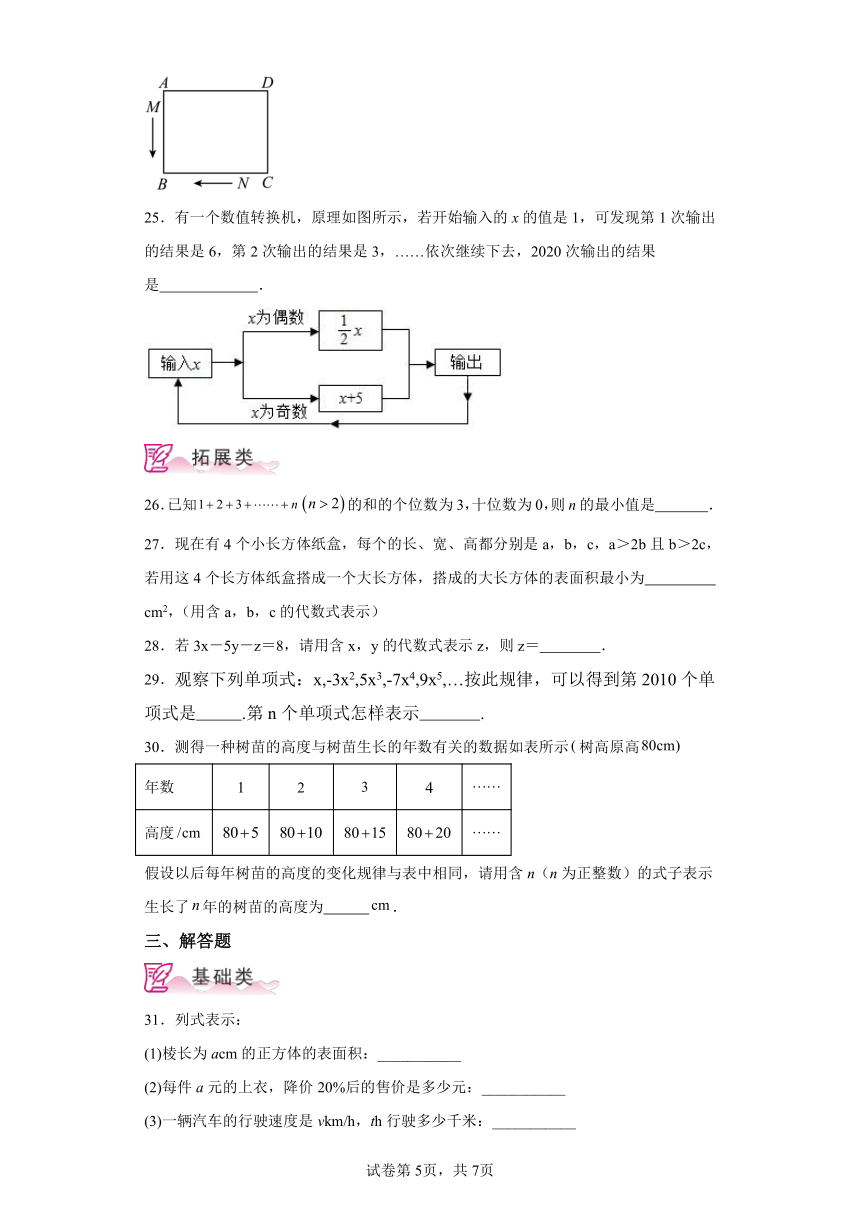
25.有一个数值转换机,原理如图所示,若开始输入的x的值是1,可发现第1次输出的结果是6,第2次输出的结果是3,……依次继续下去,2020次输出的结果是 .
26.已知的和的个位数为3,十位数为0,则n的最小值是 .
27.现在有4个小长方体纸盒,每个的长、宽、高都分别是a,b,c,a>2b且b>2c,若用这4个长方体纸盒搭成一个大长方体,搭成的大长方体的表面积最小为 cm2,(用含a,b,c的代数式表示)
28.若3x-5y-z=8,请用含x,y的代数式表示z,则z= .
29.观察下列单项式:x,-3x2,5x3,-7x4,9x5,…按此规律,可以得到第2010个单项式是 .第n个单项式怎样表示 .
30.测得一种树苗的高度与树苗生长的年数有关的数据如表所示树高原高
年数
高度
假设以后每年树苗的高度的变化规律与表中相同,请用含n(n为正整数)的式子表示生长了年的树苗的高度为 .
三、解答题
31.列式表示:
(1)棱长为acm的正方体的表面积:___________
(2)每件a元的上衣,降价20%后的售价是多少元:___________
(3)一辆汽车的行驶速度是vkm/h,th行驶多少千米:___________
(4)长方形绿地的长、宽分别是am,bm如果长增加xm,新增加的绿地面积为多少平方米:___________
(5)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数:___________
32.2022年8月3日,第二届郑州食品博览会在郑州开幕.期间河南某特产供应商进行了电商直播,其中河南干货特产头层腐竹每份6元,河南焦作铁棍山药每份10元.某时间段直播期间,河南干货特产头层腐竹共销售m份,河南焦作铁棍山药共销售n份,这两种特产共销售金额Q元.
(1)用含m,n的式子表示Q;
(2)若m为6000,n为10000,求出并用科学记数法表示Q的值.
33.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价元,乒乓球每盒定价5元,现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠两盒乒乓球;乙店的优惠办法是:全部商品按定价的折出售.某班需购买乒乓球拍4副和x盒乒乓球.
(1)当时,分别求在这两家商店购买所需支付的费用.(用含x的代数式表示)
(2)当时,分别计算在这两家商店购买所需支付的费用,如果这两种方案可以同时使用,请帮助该班设计一种最省钱的购买方案,并计算此方案所需支付的费用.
34.为了节约用水,某自来水公司采取以下收费方法:若每户每月用水不超过10吨,则每吨水收费元;若每户每月用水超过10吨,则超过的部分按每吨3元收费.8月份李老师家里用水a吨().
(1)请用含a的代数式表示李老师8月份应交的水费.
(2)当时,求李老师8月份应交水费多少元?
35.华润苏果超市有A、B、C三种果冻出售,A种果冻20千克,售价为m元每千克,B种果冻60千克,售价比A种贵2元每千克,C种果冻40千克,售价比A种便宜1元每千克.
(1)若将这三种果冻全部混合在一起销售,在保证总售价不变的情况下,混合果冻的售价应定为多少?
(2)售货员小张在写混合后的销售单价牌时,误写成原来三个单价的平均数,如果混合果冻按小张写的单价全部售完,超市的这批果冻的利润有何变化?变化多少元?
36.阅读下面的材料并解答问题:
点表示数,点表示数,点表示数,且点到点的距离记为线段的长,线段的长可以用右边的数减去左边的数表示,即.
若是最小的正整数,且满足.
(1)_________,__________.
(2)若将数轴折叠,使得与点重合:
①点与数_________表示的点重合;
②若数轴上两点之间的距离为2018(在的左侧),且两点经折叠后重合,则两点表示的数是_______、__________.
(3)点开始在数轴上运动,若点以每秒2个单位长度的速度向左运动,同时点和点分别以每秒1个单位长度和3个单位长度的速度向右运动,设运动时间为秒,试探索:的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出其值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】先写出与的和,再表示平方,则代数式即可列出.
【详解】解:与的和的平方表示为:.
故选:C.
【点睛】本题考查了列代数式,注意代数式的正确书写:数字应写在字母的前面,数字和字母之间的乘号要省略不写.
2.C
【分析】根据题意可以得到最后打折后的零售价,从而可以解答本题.
【详解】解:由题意可得, 某一型号的空气炸锅的零售价:(元),
故选C.
【点睛】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
3.A
【分析】根据代数式的书写规则逐一进行判断.
【详解】解:A、符合代数式书写规则.
B、数与字母相乘,乘号一般也省略不写,但数一定要写在字母的前面,不符合代数式书写规则,应该为,故原式不符合书写规则;
C、数与字母相乘,乘号一般也省略不写,但数一定要写在字母的前面,而且当数是带分数时一定要化为假分数,应该为,故原式不符合书写规则;
D、当代数式中含有除法运算时,一般不用“÷”号,而改用分数线,不符合代数式书写规则,应该为,故原式不符合书写规则;
故选:A.
【点睛】本题考查代数式的书写规则,解决本题的关键是熟练掌握书写规则.
4.B
【分析】根据时间=总量÷速度,列式表示即可.
【详解】解:根据题意可得:
爸爸比小明多用的时间为:分钟,
故选:B.
【点睛】本题考查了列代数式,熟练掌握时间=总量÷速度是解题关键.
5.D
【分析】根据代数式还原打折销售的方式即可得解.
【详解】解:∵甲商场需付费元,
∴甲商场付费时,100元以内不打折,超过超出100元的部分,甲商场按收费,
∵乙商场需付费元,
∴乙商场付费时,50元以内不打折,超过超出50元的部分,乙商场按收费,
∴乙商场付费时,超过超出100元的部分,乙商场按收费,
故选:D.
【点睛】此题考查了列代数式,读懂题意,明确打折销售是解题的关键.
6.C
【分析】根据题意分别列出代数式,即可一一判定.
【详解】解:A.比一个数大5,则这个数是,故该选项说法不正确;
B.表示、、的积的代数式为:,故该选项说法不正确;
C.,两数的倒数和为,故该选项说法正确;
D.与的平方差是,故该选项说法不正确;
故选:C.
【点睛】本题考查了列代数式,理解题意,正确列出代数式是解决本题的关键.
7.D
【分析】设长方形的宽为厘米,根据题意列出关系式,解即可.
【详解】解:设长方形的宽为厘米,根据题意得:
,
,
厘米.
故选:D.
【点睛】本题考查了列代数式,理解题意找到等量关系是解题的关键.
8.D
【分析】先根据题意求出女生的人数,然后与男生数求和即可.
【详解】解:∵男同学有人,女同学比男同学的少24人,
∴女同学有: 人,
∴参加比赛的学生一共有:=人.
故选D.
【点睛】本题主要考查了列代数式,读懂题意、正确根据题意列出代数式是解答本题的关键.
9.D
【分析】先表示出9月份的产值,再根据增长率的概念得出10月份产值即可.
【详解】解:由题意知,月份产值为万元,月份产值为万元,
故选:D.
【点睛】本题主要考查列代数式,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
10.D
【分析】设从学校到家路程为s,然后表示出从家到学校所用时间,再表示出从学校到家所用时间,然后利用总路程除以总时间可得平均速度.
【详解】设从学校到家路程为s,
平均速度是:
;
故选:D.
【点睛】此题主要考查了列代数式,关键是掌握平均速度=路程÷时间.
11.B
【分析】A.先涨价m%,再降价n%,则价格=100(1+m%)(1-n%)=100(1-n%+m%-)B.先涨价n%,再降价m%,价格=100(1+n%)(1-m%)=100(1+n%-m%-),则B<A;C.先涨价,再降价,则价格=100(1+)(1-)=100,推出BC,得到A>C>B,D选项错误.
【详解】A.先涨价m%,再降价n%,
则价格为:100(1+m%)(1-n%)=100(1-n%+m%- )
B.先涨价n%,再降价m%,
价格为:100(1+n%)(1-m%)=100(1+n%-m%- )
则B<A
C先涨价,再降价,
则价格为:100(1+)(1-)
=100 ,
B-C
,
∴BA-C
,
∴A>C,
∵D选项错误,
∴A>C>B.
故选B.
【点睛】本题主要考查了不同降价方案的销售问题,解决问题的关键是熟练掌握降价后的售价等于原价乘以1减去降价率的差,列式比较大小,售价最小的为价格最低方案.
12.C
【分析】根据中位线定理及等边三角形得到三条中线相等且都等于等边三角形的边的一半,等到作一次图得3个菱形,依次可得答案.
【详解】解:由题意可得,
∵、、分别是等边 的边、、的中点,
∴ ,
∴图1有三个菱形,由此可得作一次中位线分三个菱形,
∴第n个图形中菱形的个数共有 个菱形,
故选C.
【点睛】本题考查等边三角形性质及中位线定理,解题的关键是找出作一次中位线分3个菱形.
13.C
【分析】观察不难发现,底数是两个连续整数的乘积的一半,根据此规律写出即可.
【详解】解:∵,,,,,
∴,,,,,
∴,
故选:C.
【点睛】本题是对数字变化规律的考查,难度较大,对同学们的数字敏感程度要求较高,观察出底数的变化特点是解题的关键.
14.C
【分析】由已知可得规律:,根据规律求出
【详解】由已知可得规律:,
因为,
所以,
所以,
故选C
【点睛】本题考查了用代数式表示规律,观察分析出规律是解题的关键.
15.D
【分析】观察图形、、,找到个数规律为,进而写出第个图形中小黑点的个数,即可求解.
【详解】由图形、、可以看出,第个图形小黑点的个数:;
第个图形小黑点的个数:;
第个图形小黑点的个数:;
则第个图形小黑点的个数:;
第个图形小黑点的个数:.
故选D.
【点睛】本题考查了图形类规律,找到规律是解题的关键.
16. 前面 假分数
【解析】略
17.
【分析】根据运算程序式列出y与x之间的关系式即可.
【详解】解:由运算程序得,
故答案为:.
【点睛】本题主要考查了程序运算式,解题的关键是理解题意,根据运算程序列出代数式.
18.
【分析】根据题意可直接进行求解.
【详解】解:由题意得该苹果现价是每千克元;
故答案为:.
【点睛】本题主要考查列代数式,解题的关键是理解题意.
19.
【分析】分别表示在两条路上所用的时间,作差即可求得.
【详解】解:第一条路所用时间:,
第二条路所用时间:,
第二条路比走第一条路多用的时间为:
故答案为:.
【点睛】本题考查了速度,路程,时间之间的关系,解题的关键是理解题意,掌握速度,路程,时间之间的关系.
20.(答案不唯一)
【分析】可以有多种表示方法:①横向来看,左右两个数的差都是1;②纵向看,上下两个数字的差相等;③对角线的角度看,两个数字的和相等.
【详解】解:横向来看(答案不唯一)
②纵向看,则.
③对角线的角度看,
故答案为:(答案不唯一)
【点睛】本题考查了列代数式,观察日历中的数字找到四个数的关系是解题的关键.
21.
【分析】根据“十位数字乘以10加上个位数字等于这个两位数”,列代数式即可.
【详解】一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是
故答案为:12a
【点睛】本题主要考查了列代数式,熟练掌握两位数的表示方法是解题的关键.
22.
【分析】根据共有m人参加晚托课后服务,其中有参加足球兴趣活动,有8人参加书法兴趣活动,即可求得参加其余兴趣活动的人数.
【详解】解:共有m人参加晚托课后服务,其中有参加足球兴趣活动,有8人参加书法兴趣活动,
参加其余兴趣活动的人数为:,
故答案:.
【点睛】本题考查了列代数式,理解题意,正确列出代数式是解决本题的关键.
23.
【分析】观察图可知房间窗户的面积是,先利用圆的面积,求出窗帘的面积,也就是遮住阳光的面积,进而用总面积减去遮住的面积即可求得.
【详解】解:根据题意和图可得,窗帘所在圆的半径为,
故窗户中能射进阳光的部分的面积为:
,
故答案为:.
【点睛】本题考查了圆的面积公式,矩形的面积公式,熟练掌握和运用各图形面积的求法是解决本题的关键.
24.
【分析】根据相遇时间总路程速度和得出第一次相遇的时间,再分别求出第二、三、四次相遇的时间,得出规律,进而求出第n次相遇的时间.
【详解】解:根据题意得,当M、N两点第一次相遇时,(秒),
从第一次相遇到第二次相遇需要的时间为:(秒),
∴当M、N两点第二次相遇时,(秒),
从第二次相遇到第三次相遇需要的时间为:(秒),
∴当M、N两点第三次相遇时,(秒),
从第三次相遇到第四次相遇需要的时间为:(秒),
∴当M、N两点第四次相遇时,(秒),
以此类推,
∴第n次相遇时,(秒).
∴第10次相遇时,(秒).
故答案为:;.
【点睛】本题考查了列代数式,掌握相遇问题的数量关系是解题的关键.
25.4
【分析】根据原理图可算出每一次输出的结果,从中找出规律即可求出第2020次的结果.
【详解】解:根据原理图可知:
当x=1时,第一次输出的结果为6,
第二次输出的结果为3,
第三次输出的结果为8,
第四次输出的结果为4,
第五次输出的结果为2,
第六次输出的结果为1,
第七次输出的结果为6,
所以从第一次开始,每6次重复一遍,
2020÷6=336...4,
所以第2020次输出的结果是4.
故答案为:4.
【点睛】本题考查有理数的混合运算,代数式求值,涉及数字规律问题,属于中等题型.
26.37
【分析】由题意知,则,由的和的个位数为3,十位数为0,可得的末两位是06,末位是6的连续的两个自然数的成积的末位只能为或,然后列举不同的值,计算求出满足要求的值即可.
【详解】解:由题意知,
∴,
∵的和的个位数为3,十位数为0,
∴的末两位是06,
∵末位是6的连续的两个自然数的成积的末位只能为或,
∴,(不合要求)
,(不合要求)
,(不合要求)
,(不合要求)
,(不合要求)
,
∴n的最小值为37;
故答案为:37.
【点睛】本题考查了列代数式运算求解.解题的关键在于根据题意确定前项和的表示形式.
27.4ab+4ac+8bc
【分析】分四个小长方体排一行以及两行来寻找搭法,由此可得出共6种不同的搭建方式,再根据长方体的表面积公式结合a>2b、b>2c即可得出大长方体的表面积最小值.
【详解】解:四个小长方体排一行时,有3种不同的搭法;四个小长方体排两行时,有3种不同的搭法.
∴用这4个长方体纸盒搭成一个大长方体,共有6种不同的方法.
∵a>2b且b>2c,
∴搭成的大长方体的表面积最小为:4×2×(ab+ac+bc)-4×(ab+ac)=4(ab+ac+2bc)cm2.
故答案为:4ab+4ac+8bc.
【点睛】本题考查了几何体的表面积,分两类搭建方式寻找搭法是解题的关键.
28.3x-5y-8
【分析】根据等式的性质,移项即可解题.
【详解】解:∵3x-5y-z=8,
∴z=3x-5y-8(移项).
【点睛】本题考查了等式的性质,属于简单题,熟练运用移项是解题关键.
29. -4019 x2010 (-1)(n+1)(2n-1)n
【详解】观察下列单项式:x,-3x2,5x3,-7x4,9x5,…
得出第n项的系数可以表示为(-1)n-1(2n-1),指数表示为n,
即第n项表示为(-1)n-1(2n-1)xn,
第2008个单项式是-4015x2008,
故答案为-4015x2008;(-1)n-1(2n-1)xn.
【点睛】本题考查根据规律写单项式,通过仔细观察写出第n个单项式是解此题关键.
30.##
【分析】从上表可以看出,树每年长高,所以生长了n年的树苗的高度为.
【详解】解:从表格可看出,每年树长高,
年的树高为.
故答案为:.
【点睛】本题主要考查了列代数式,解题的关键是算出树每年长高多少厘米,通过观察,分析、归纳并发现其中的规律.
31.(1);
(2);
(3);
(4);
(5)
【分析】(1)根据正方体的表面积公式求解即可;
(2)根据售价=原价×即可求解;
(3)根据路程=速度×时间即可求解;
(4)根据长方形的面积公式即可求解;
(5)根据十位数字×10+各位数字=两位数,即可求解.
【详解】(1)解:棱长为acm的正方体的表面积:,
故答案为:;
(2)解:每件a元的上衣,降价20%后的售价是(元),
故答案为:;
(3)解:一辆汽车的行驶速度是vkm/h,th行驶千米,
故答案为:;
(4)解:由题意得:(平方米),
故答案为:;
(5)解:两位数的个位上的数是a,十位上的数是b,表示为:,
故答案为:.
【点睛】本题主要考查列代数式,理解题意,找出题中的数量关系是关键.
32.(1)
(2),
【分析】(1)根据题意列出销售金额Q的代数式即可;
(2)把,代入销售金额Q的代数式计算结果,再用科学记数法表示即可.
【详解】(1)∵头层腐竹每份6元,铁棍山药每份10元,头层腐竹共销售m份,铁棍山药共销售n份,这两种特产共销售金额Q元,
∴;
(2)当,时,,
用科学记数法表示为.
【点睛】本题考查了列代数式营销问题,科学记数法,理解题意列出相关代数式是解题的关键.
33.(1)甲商店费用为:元,乙商店费用为:元;
(2)甲店费用220元,乙店费用221元;先在甲商店购买4副乒乓球拍,再在乙商店购买盒乒乓球,所需支付的费用为元.
【分析】(1)根据优惠方案结合金额单价数量列式即可得到答案;
(2)将代入(1)中代数式求解,即可得到答案.
【详解】(1)解:由题意可得,
甲商店费用:元,
乙商店费用:元,
∴甲商店费用为:元,乙商店费用为:元;
(2)解:当时,
甲商店:(元),
乙商店:(元),
如果两种方案能同时使用,可先在甲商店购买4副乒乓球拍,再在乙商店购买盒乒乓球,此时最省钱,
所需支付的费用为:(元).
【点睛】本题考查列代数式及求值,解题的关键是从题干中找到数量关系,列出代数式.
34.(1)
(2)35元
【分析】(1)根据收费标准即可列出代数式;
(2)把代入(1)中的代数式,求值即可.
【详解】(1)
(2)当时
【点睛】此题考查列代数式,代数式求值,解题关键在于根据题意列出式子.
35.(1)元;(2)这批果冻的利润将减少,减少40元.
【分析】(1)计算出所有果冻的总售价及总质量,利用单价等于售价除以质量即可得到答案;
计算三个单价的平均数时的总售价,及(1)中混合果冻的总售价,两种相减即可得到答案.
【详解】(1) ,
=,
=()元,
∴混合果冻的售价应定为()元;
(2)
(元),
所以如果按小张写的单价全部售完,这批果冻的利润将减少,减少40元.
【点睛】此题考查列代数式解决问题,正确理解题意是解题的关键.
36.(1)1,5;(2)①3;②-1007,1011;(3)不变,值为8
【分析】(1)利用非负性可求解;
(2)①由中点坐标公式可求AC的中点表示的数是2,由折叠的性质可求解;
②由折叠的性质可求解;
(3)利用两点距离公式分别求出AC,AB,表示出3AC-5AB,再化简即可求解.
【详解】解:(1)∵b是最小的正整数,
∴b=1,
∵(c-5)2+|a+b|=0.
∴c=5,a=-b=-1,
故答案为:1,5;
(2)①∵将数轴折叠,使得A与C点重合:
∴AC的中点表示的数是(-1+5)÷2=2,
∴与点B重合的数=2-1+2=3;
②点P表示的数为2-2018÷2=-1007,
点Q表示的数为2+2018÷2=1011,
故答案为:-1007,1011;
(3)3AC-5AB的值不变.
理由是:
点A表示的数为:-1-2t,
点B表示的数为:1+t,
点C表示的数为:5+3t,
∴AC=5+3t-(-1-2t)=6+5t,AB=1+t-(-1-2t)=2+3t,
3AC-5AB=3(6+5t)-5(2+3t)=8,
所以3AC-5AB的值不变,为8.
【点睛】本题考查了数轴,非负性,折叠的性质,两点距离公式,灵活运用这些性质解决问题是本题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.用代数式表示“与的和的平方”,正确的是( )
A. B. C. D.
2.某商店经销一种品牌的空气炸锅,其中某一型号的空气炸锅的进价为每台元,商店将进价提高30%后作为零售价销售,一段时间后,商店又按零售价的8折销售,这时该型号空气炸锅的零售价为( )
A.元 B.元 C.元 D.元
3.下列各式中,符合代数式书写规则的是( )
A. B. C. D.
4.小明在电脑上1分钟录入汉字50个,小明的爸爸1分钟录入汉字30个.如果小明和爸爸各录入个汉字,那么爸爸比小明多用( )分钟.
A. B. C. D.
5.甲,乙两商场以相同的价格出售同样的商品,当购物金额超出一定数额后,各自推出不同的优惠方案,若在两个商场购买元的商品,在甲商场需付费元,在乙商场需付费元,下列关于两个商场优惠方案的说法正确的是( )
A.购买金额不超过100元时,两个商场都不优惠
B.购买金额超过50元时,两个商场都有优惠
C.购买金额超过100元时,甲商场按收费,乙商场按收费
D.购买金额超过100元时,超出100元的部分,甲商场按收费,乙商场按收费
6.下面语句中,正确的是( )
A.比一个数大5,则这个数是 B.表示、、的积的代数式为
C.,两数的倒数和为 D.与的平方差是
7.一个长方形的长是宽的4倍多2厘米,设长为厘米,那么宽为( )
A.厘米 B.厘米 C.厘米 D.厘米
8.今年,我校成功举办了“经典诵读”比赛,其中参加比赛的男同学有人,女同学人数比男同学人数的少24人,则参加“经典诵读”比赛的学生一共有( )
A.人 B.人 C.人 D.人
9.受今年高温天气的影响,我市某企业今年月份产值为万元,月份比月份减少了,月份比月份增加了,则月份的产值为( )
A.万元 B.万元
C.万元 D.万元
10.粗心的小倩在放学回家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回家(取书时间忽略不计).已知跑步速度为x,步行速度为y,则她往返一趟的平均速度是( )
A.x B.y C. D.
11.因H7N9禽流感致病性强,某药房打算让利于民,板蓝根一箱原价为100元,现有下列四种调价方案,其中0<n<m<100,则调价后板蓝根价格最低的方案是( )
A.先涨价m%,再降价n% B.先涨价n%,再降价m%
C.先涨价,再降价再降价 D.无法确定
12.如图,在图1中,、、分别是等边 的边、、的中点,在图2中,,,分别是的边、、的中点,…,按此规律,则第n个图形中菱形的个数共有( )个.
A. B. C. D.
13.观察算式,探究规律:
当时,;
当时, ;
当时,;
当时,;…
那么与n的关系为( )
A. B. C. D.
14.已知,,,,若,都是正整数符合前面式子的规律,则的值是( )
A.17 B.18 C.19 D.20
15.观察下列一组图形,其中图中共有个小黑点,图中共有个小黑点,图中共有个小黑点,,按此规律,图中小黑点的个数是( )
A.46 B.51 C.61 D.76
二、填空题
16.书写单项式的注意事项:
①数字要写在字母的 ;
②数字与字母相乘,字母与字母相乘时,“×”号可以省略或用 替代;
③系数是带分数时要写成 .
17.如图是小明同学设计的一个运算程序的流程图,输入一个有理数x,便可输出一个相应的有理数y,写出y与x之间的关系式: .
18.苹果原价是每千克x元,按9折优惠出售,该苹果现价是每千克 元.(用含x的代数式表示)
19.从甲地到乙地有两条都是3千米的路,其中第一条是平路,第二条是1千米的上坡路,2千米的下坡路:小明在上坡路上的骑车速度为千米/时,在平路上的骑车速度为千米/时,在下坡路上的骑车速度为千米/时,则他走第二条路比走第一条路多用了 小时.(用含的代数式表示)
20.如图所示是2004年10月份的日历.现在日历中任意框出4个数,请用一个等式表示,,,之间的关系: .
21.一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是 .
22.某校初一(1)班有m人参加晚托课后服务,其中有参加足球兴趣活动,有8人参加书法兴趣活动,则参加其余兴趣活动的共 人.
23.小红的房间窗户的装饰物如图所示,由两个四分之一圆组成(半径分别相同),窗户中能射进阳光的部分的面积是 .
24.如图,长方形中,,,M、N两点分别从点A、C同时出发,沿长方形的边相向而行,速度都是秒,设他们的运动时间为t秒,当M、N两点第一次相遇时, 秒;第十次相遇时, 秒.
25.有一个数值转换机,原理如图所示,若开始输入的x的值是1,可发现第1次输出的结果是6,第2次输出的结果是3,……依次继续下去,2020次输出的结果是 .
26.已知的和的个位数为3,十位数为0,则n的最小值是 .
27.现在有4个小长方体纸盒,每个的长、宽、高都分别是a,b,c,a>2b且b>2c,若用这4个长方体纸盒搭成一个大长方体,搭成的大长方体的表面积最小为 cm2,(用含a,b,c的代数式表示)
28.若3x-5y-z=8,请用含x,y的代数式表示z,则z= .
29.观察下列单项式:x,-3x2,5x3,-7x4,9x5,…按此规律,可以得到第2010个单项式是 .第n个单项式怎样表示 .
30.测得一种树苗的高度与树苗生长的年数有关的数据如表所示树高原高
年数
高度
假设以后每年树苗的高度的变化规律与表中相同,请用含n(n为正整数)的式子表示生长了年的树苗的高度为 .
三、解答题
31.列式表示:
(1)棱长为acm的正方体的表面积:___________
(2)每件a元的上衣,降价20%后的售价是多少元:___________
(3)一辆汽车的行驶速度是vkm/h,th行驶多少千米:___________
(4)长方形绿地的长、宽分别是am,bm如果长增加xm,新增加的绿地面积为多少平方米:___________
(5)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数:___________
32.2022年8月3日,第二届郑州食品博览会在郑州开幕.期间河南某特产供应商进行了电商直播,其中河南干货特产头层腐竹每份6元,河南焦作铁棍山药每份10元.某时间段直播期间,河南干货特产头层腐竹共销售m份,河南焦作铁棍山药共销售n份,这两种特产共销售金额Q元.
(1)用含m,n的式子表示Q;
(2)若m为6000,n为10000,求出并用科学记数法表示Q的值.
33.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价元,乒乓球每盒定价5元,现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠两盒乒乓球;乙店的优惠办法是:全部商品按定价的折出售.某班需购买乒乓球拍4副和x盒乒乓球.
(1)当时,分别求在这两家商店购买所需支付的费用.(用含x的代数式表示)
(2)当时,分别计算在这两家商店购买所需支付的费用,如果这两种方案可以同时使用,请帮助该班设计一种最省钱的购买方案,并计算此方案所需支付的费用.
34.为了节约用水,某自来水公司采取以下收费方法:若每户每月用水不超过10吨,则每吨水收费元;若每户每月用水超过10吨,则超过的部分按每吨3元收费.8月份李老师家里用水a吨().
(1)请用含a的代数式表示李老师8月份应交的水费.
(2)当时,求李老师8月份应交水费多少元?
35.华润苏果超市有A、B、C三种果冻出售,A种果冻20千克,售价为m元每千克,B种果冻60千克,售价比A种贵2元每千克,C种果冻40千克,售价比A种便宜1元每千克.
(1)若将这三种果冻全部混合在一起销售,在保证总售价不变的情况下,混合果冻的售价应定为多少?
(2)售货员小张在写混合后的销售单价牌时,误写成原来三个单价的平均数,如果混合果冻按小张写的单价全部售完,超市的这批果冻的利润有何变化?变化多少元?
36.阅读下面的材料并解答问题:
点表示数,点表示数,点表示数,且点到点的距离记为线段的长,线段的长可以用右边的数减去左边的数表示,即.
若是最小的正整数,且满足.
(1)_________,__________.
(2)若将数轴折叠,使得与点重合:
①点与数_________表示的点重合;
②若数轴上两点之间的距离为2018(在的左侧),且两点经折叠后重合,则两点表示的数是_______、__________.
(3)点开始在数轴上运动,若点以每秒2个单位长度的速度向左运动,同时点和点分别以每秒1个单位长度和3个单位长度的速度向右运动,设运动时间为秒,试探索:的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出其值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】先写出与的和,再表示平方,则代数式即可列出.
【详解】解:与的和的平方表示为:.
故选:C.
【点睛】本题考查了列代数式,注意代数式的正确书写:数字应写在字母的前面,数字和字母之间的乘号要省略不写.
2.C
【分析】根据题意可以得到最后打折后的零售价,从而可以解答本题.
【详解】解:由题意可得, 某一型号的空气炸锅的零售价:(元),
故选C.
【点睛】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
3.A
【分析】根据代数式的书写规则逐一进行判断.
【详解】解:A、符合代数式书写规则.
B、数与字母相乘,乘号一般也省略不写,但数一定要写在字母的前面,不符合代数式书写规则,应该为,故原式不符合书写规则;
C、数与字母相乘,乘号一般也省略不写,但数一定要写在字母的前面,而且当数是带分数时一定要化为假分数,应该为,故原式不符合书写规则;
D、当代数式中含有除法运算时,一般不用“÷”号,而改用分数线,不符合代数式书写规则,应该为,故原式不符合书写规则;
故选:A.
【点睛】本题考查代数式的书写规则,解决本题的关键是熟练掌握书写规则.
4.B
【分析】根据时间=总量÷速度,列式表示即可.
【详解】解:根据题意可得:
爸爸比小明多用的时间为:分钟,
故选:B.
【点睛】本题考查了列代数式,熟练掌握时间=总量÷速度是解题关键.
5.D
【分析】根据代数式还原打折销售的方式即可得解.
【详解】解:∵甲商场需付费元,
∴甲商场付费时,100元以内不打折,超过超出100元的部分,甲商场按收费,
∵乙商场需付费元,
∴乙商场付费时,50元以内不打折,超过超出50元的部分,乙商场按收费,
∴乙商场付费时,超过超出100元的部分,乙商场按收费,
故选:D.
【点睛】此题考查了列代数式,读懂题意,明确打折销售是解题的关键.
6.C
【分析】根据题意分别列出代数式,即可一一判定.
【详解】解:A.比一个数大5,则这个数是,故该选项说法不正确;
B.表示、、的积的代数式为:,故该选项说法不正确;
C.,两数的倒数和为,故该选项说法正确;
D.与的平方差是,故该选项说法不正确;
故选:C.
【点睛】本题考查了列代数式,理解题意,正确列出代数式是解决本题的关键.
7.D
【分析】设长方形的宽为厘米,根据题意列出关系式,解即可.
【详解】解:设长方形的宽为厘米,根据题意得:
,
,
厘米.
故选:D.
【点睛】本题考查了列代数式,理解题意找到等量关系是解题的关键.
8.D
【分析】先根据题意求出女生的人数,然后与男生数求和即可.
【详解】解:∵男同学有人,女同学比男同学的少24人,
∴女同学有: 人,
∴参加比赛的学生一共有:=人.
故选D.
【点睛】本题主要考查了列代数式,读懂题意、正确根据题意列出代数式是解答本题的关键.
9.D
【分析】先表示出9月份的产值,再根据增长率的概念得出10月份产值即可.
【详解】解:由题意知,月份产值为万元,月份产值为万元,
故选:D.
【点睛】本题主要考查列代数式,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
10.D
【分析】设从学校到家路程为s,然后表示出从家到学校所用时间,再表示出从学校到家所用时间,然后利用总路程除以总时间可得平均速度.
【详解】设从学校到家路程为s,
平均速度是:
;
故选:D.
【点睛】此题主要考查了列代数式,关键是掌握平均速度=路程÷时间.
11.B
【分析】A.先涨价m%,再降价n%,则价格=100(1+m%)(1-n%)=100(1-n%+m%-)B.先涨价n%,再降价m%,价格=100(1+n%)(1-m%)=100(1+n%-m%-),则B<A;C.先涨价,再降价,则价格=100(1+)(1-)=100,推出B
【详解】A.先涨价m%,再降价n%,
则价格为:100(1+m%)(1-n%)=100(1-n%+m%- )
B.先涨价n%,再降价m%,
价格为:100(1+n%)(1-m%)=100(1+n%-m%- )
则B<A
C先涨价,再降价,
则价格为:100(1+)(1-)
=100 ,
B-C
,
∴B
,
∴A>C,
∵D选项错误,
∴A>C>B.
故选B.
【点睛】本题主要考查了不同降价方案的销售问题,解决问题的关键是熟练掌握降价后的售价等于原价乘以1减去降价率的差,列式比较大小,售价最小的为价格最低方案.
12.C
【分析】根据中位线定理及等边三角形得到三条中线相等且都等于等边三角形的边的一半,等到作一次图得3个菱形,依次可得答案.
【详解】解:由题意可得,
∵、、分别是等边 的边、、的中点,
∴ ,
∴图1有三个菱形,由此可得作一次中位线分三个菱形,
∴第n个图形中菱形的个数共有 个菱形,
故选C.
【点睛】本题考查等边三角形性质及中位线定理,解题的关键是找出作一次中位线分3个菱形.
13.C
【分析】观察不难发现,底数是两个连续整数的乘积的一半,根据此规律写出即可.
【详解】解:∵,,,,,
∴,,,,,
∴,
故选:C.
【点睛】本题是对数字变化规律的考查,难度较大,对同学们的数字敏感程度要求较高,观察出底数的变化特点是解题的关键.
14.C
【分析】由已知可得规律:,根据规律求出
【详解】由已知可得规律:,
因为,
所以,
所以,
故选C
【点睛】本题考查了用代数式表示规律,观察分析出规律是解题的关键.
15.D
【分析】观察图形、、,找到个数规律为,进而写出第个图形中小黑点的个数,即可求解.
【详解】由图形、、可以看出,第个图形小黑点的个数:;
第个图形小黑点的个数:;
第个图形小黑点的个数:;
则第个图形小黑点的个数:;
第个图形小黑点的个数:.
故选D.
【点睛】本题考查了图形类规律,找到规律是解题的关键.
16. 前面 假分数
【解析】略
17.
【分析】根据运算程序式列出y与x之间的关系式即可.
【详解】解:由运算程序得,
故答案为:.
【点睛】本题主要考查了程序运算式,解题的关键是理解题意,根据运算程序列出代数式.
18.
【分析】根据题意可直接进行求解.
【详解】解:由题意得该苹果现价是每千克元;
故答案为:.
【点睛】本题主要考查列代数式,解题的关键是理解题意.
19.
【分析】分别表示在两条路上所用的时间,作差即可求得.
【详解】解:第一条路所用时间:,
第二条路所用时间:,
第二条路比走第一条路多用的时间为:
故答案为:.
【点睛】本题考查了速度,路程,时间之间的关系,解题的关键是理解题意,掌握速度,路程,时间之间的关系.
20.(答案不唯一)
【分析】可以有多种表示方法:①横向来看,左右两个数的差都是1;②纵向看,上下两个数字的差相等;③对角线的角度看,两个数字的和相等.
【详解】解:横向来看(答案不唯一)
②纵向看,则.
③对角线的角度看,
故答案为:(答案不唯一)
【点睛】本题考查了列代数式,观察日历中的数字找到四个数的关系是解题的关键.
21.
【分析】根据“十位数字乘以10加上个位数字等于这个两位数”,列代数式即可.
【详解】一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是
故答案为:12a
【点睛】本题主要考查了列代数式,熟练掌握两位数的表示方法是解题的关键.
22.
【分析】根据共有m人参加晚托课后服务,其中有参加足球兴趣活动,有8人参加书法兴趣活动,即可求得参加其余兴趣活动的人数.
【详解】解:共有m人参加晚托课后服务,其中有参加足球兴趣活动,有8人参加书法兴趣活动,
参加其余兴趣活动的人数为:,
故答案:.
【点睛】本题考查了列代数式,理解题意,正确列出代数式是解决本题的关键.
23.
【分析】观察图可知房间窗户的面积是,先利用圆的面积,求出窗帘的面积,也就是遮住阳光的面积,进而用总面积减去遮住的面积即可求得.
【详解】解:根据题意和图可得,窗帘所在圆的半径为,
故窗户中能射进阳光的部分的面积为:
,
故答案为:.
【点睛】本题考查了圆的面积公式,矩形的面积公式,熟练掌握和运用各图形面积的求法是解决本题的关键.
24.
【分析】根据相遇时间总路程速度和得出第一次相遇的时间,再分别求出第二、三、四次相遇的时间,得出规律,进而求出第n次相遇的时间.
【详解】解:根据题意得,当M、N两点第一次相遇时,(秒),
从第一次相遇到第二次相遇需要的时间为:(秒),
∴当M、N两点第二次相遇时,(秒),
从第二次相遇到第三次相遇需要的时间为:(秒),
∴当M、N两点第三次相遇时,(秒),
从第三次相遇到第四次相遇需要的时间为:(秒),
∴当M、N两点第四次相遇时,(秒),
以此类推,
∴第n次相遇时,(秒).
∴第10次相遇时,(秒).
故答案为:;.
【点睛】本题考查了列代数式,掌握相遇问题的数量关系是解题的关键.
25.4
【分析】根据原理图可算出每一次输出的结果,从中找出规律即可求出第2020次的结果.
【详解】解:根据原理图可知:
当x=1时,第一次输出的结果为6,
第二次输出的结果为3,
第三次输出的结果为8,
第四次输出的结果为4,
第五次输出的结果为2,
第六次输出的结果为1,
第七次输出的结果为6,
所以从第一次开始,每6次重复一遍,
2020÷6=336...4,
所以第2020次输出的结果是4.
故答案为:4.
【点睛】本题考查有理数的混合运算,代数式求值,涉及数字规律问题,属于中等题型.
26.37
【分析】由题意知,则,由的和的个位数为3,十位数为0,可得的末两位是06,末位是6的连续的两个自然数的成积的末位只能为或,然后列举不同的值,计算求出满足要求的值即可.
【详解】解:由题意知,
∴,
∵的和的个位数为3,十位数为0,
∴的末两位是06,
∵末位是6的连续的两个自然数的成积的末位只能为或,
∴,(不合要求)
,(不合要求)
,(不合要求)
,(不合要求)
,(不合要求)
,
∴n的最小值为37;
故答案为:37.
【点睛】本题考查了列代数式运算求解.解题的关键在于根据题意确定前项和的表示形式.
27.4ab+4ac+8bc
【分析】分四个小长方体排一行以及两行来寻找搭法,由此可得出共6种不同的搭建方式,再根据长方体的表面积公式结合a>2b、b>2c即可得出大长方体的表面积最小值.
【详解】解:四个小长方体排一行时,有3种不同的搭法;四个小长方体排两行时,有3种不同的搭法.
∴用这4个长方体纸盒搭成一个大长方体,共有6种不同的方法.
∵a>2b且b>2c,
∴搭成的大长方体的表面积最小为:4×2×(ab+ac+bc)-4×(ab+ac)=4(ab+ac+2bc)cm2.
故答案为:4ab+4ac+8bc.
【点睛】本题考查了几何体的表面积,分两类搭建方式寻找搭法是解题的关键.
28.3x-5y-8
【分析】根据等式的性质,移项即可解题.
【详解】解:∵3x-5y-z=8,
∴z=3x-5y-8(移项).
【点睛】本题考查了等式的性质,属于简单题,熟练运用移项是解题关键.
29. -4019 x2010 (-1)(n+1)(2n-1)n
【详解】观察下列单项式:x,-3x2,5x3,-7x4,9x5,…
得出第n项的系数可以表示为(-1)n-1(2n-1),指数表示为n,
即第n项表示为(-1)n-1(2n-1)xn,
第2008个单项式是-4015x2008,
故答案为-4015x2008;(-1)n-1(2n-1)xn.
【点睛】本题考查根据规律写单项式,通过仔细观察写出第n个单项式是解此题关键.
30.##
【分析】从上表可以看出,树每年长高,所以生长了n年的树苗的高度为.
【详解】解:从表格可看出,每年树长高,
年的树高为.
故答案为:.
【点睛】本题主要考查了列代数式,解题的关键是算出树每年长高多少厘米,通过观察,分析、归纳并发现其中的规律.
31.(1);
(2);
(3);
(4);
(5)
【分析】(1)根据正方体的表面积公式求解即可;
(2)根据售价=原价×即可求解;
(3)根据路程=速度×时间即可求解;
(4)根据长方形的面积公式即可求解;
(5)根据十位数字×10+各位数字=两位数,即可求解.
【详解】(1)解:棱长为acm的正方体的表面积:,
故答案为:;
(2)解:每件a元的上衣,降价20%后的售价是(元),
故答案为:;
(3)解:一辆汽车的行驶速度是vkm/h,th行驶千米,
故答案为:;
(4)解:由题意得:(平方米),
故答案为:;
(5)解:两位数的个位上的数是a,十位上的数是b,表示为:,
故答案为:.
【点睛】本题主要考查列代数式,理解题意,找出题中的数量关系是关键.
32.(1)
(2),
【分析】(1)根据题意列出销售金额Q的代数式即可;
(2)把,代入销售金额Q的代数式计算结果,再用科学记数法表示即可.
【详解】(1)∵头层腐竹每份6元,铁棍山药每份10元,头层腐竹共销售m份,铁棍山药共销售n份,这两种特产共销售金额Q元,
∴;
(2)当,时,,
用科学记数法表示为.
【点睛】本题考查了列代数式营销问题,科学记数法,理解题意列出相关代数式是解题的关键.
33.(1)甲商店费用为:元,乙商店费用为:元;
(2)甲店费用220元,乙店费用221元;先在甲商店购买4副乒乓球拍,再在乙商店购买盒乒乓球,所需支付的费用为元.
【分析】(1)根据优惠方案结合金额单价数量列式即可得到答案;
(2)将代入(1)中代数式求解,即可得到答案.
【详解】(1)解:由题意可得,
甲商店费用:元,
乙商店费用:元,
∴甲商店费用为:元,乙商店费用为:元;
(2)解:当时,
甲商店:(元),
乙商店:(元),
如果两种方案能同时使用,可先在甲商店购买4副乒乓球拍,再在乙商店购买盒乒乓球,此时最省钱,
所需支付的费用为:(元).
【点睛】本题考查列代数式及求值,解题的关键是从题干中找到数量关系,列出代数式.
34.(1)
(2)35元
【分析】(1)根据收费标准即可列出代数式;
(2)把代入(1)中的代数式,求值即可.
【详解】(1)
(2)当时
【点睛】此题考查列代数式,代数式求值,解题关键在于根据题意列出式子.
35.(1)元;(2)这批果冻的利润将减少,减少40元.
【分析】(1)计算出所有果冻的总售价及总质量,利用单价等于售价除以质量即可得到答案;
计算三个单价的平均数时的总售价,及(1)中混合果冻的总售价,两种相减即可得到答案.
【详解】(1) ,
=,
=()元,
∴混合果冻的售价应定为()元;
(2)
(元),
所以如果按小张写的单价全部售完,这批果冻的利润将减少,减少40元.
【点睛】此题考查列代数式解决问题,正确理解题意是解题的关键.
36.(1)1,5;(2)①3;②-1007,1011;(3)不变,值为8
【分析】(1)利用非负性可求解;
(2)①由中点坐标公式可求AC的中点表示的数是2,由折叠的性质可求解;
②由折叠的性质可求解;
(3)利用两点距离公式分别求出AC,AB,表示出3AC-5AB,再化简即可求解.
【详解】解:(1)∵b是最小的正整数,
∴b=1,
∵(c-5)2+|a+b|=0.
∴c=5,a=-b=-1,
故答案为:1,5;
(2)①∵将数轴折叠,使得A与C点重合:
∴AC的中点表示的数是(-1+5)÷2=2,
∴与点B重合的数=2-1+2=3;
②点P表示的数为2-2018÷2=-1007,
点Q表示的数为2+2018÷2=1011,
故答案为:-1007,1011;
(3)3AC-5AB的值不变.
理由是:
点A表示的数为:-1-2t,
点B表示的数为:1+t,
点C表示的数为:5+3t,
∴AC=5+3t-(-1-2t)=6+5t,AB=1+t-(-1-2t)=2+3t,
3AC-5AB=3(6+5t)-5(2+3t)=8,
所以3AC-5AB的值不变,为8.
【点睛】本题考查了数轴,非负性,折叠的性质,两点距离公式,灵活运用这些性质解决问题是本题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
