专题3.14探索与表达规律 分层练习(含解析)2023-2024学年七年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题3.14探索与表达规律 分层练习(含解析)2023-2024学年七年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览




文档简介
专题3.14 探索与表达规律(分层练习)
一、单选题
1.观察一组数据:3,5,7,9,……,那么第(是自然数)个数据是( )
A. B. C. D.
2.如图所示的运算程序中,若开始输入的值为,我们发现第次输出的结果为,第次输出的结果为,…第次输出的结果为( )
A. B. C. D.
3.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,…,通过观察,找出规律,确定32021的个位数字是( )
A.3 B.9 C.7 D.1
4.下列图形都是由同样大小的★按照一定规律组成的,其中第①个图形中共有个★,第②个图形中共有个★,第③个图形中共有个★,…,按此规律排列下去,第⑥个图形中的★个数为( )
A.个 B.个 C.个 D.个
5.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动算一次,则滚动第2021次后,骰子朝下一面的点数是( )
A.5 B.3 C.4 D.2
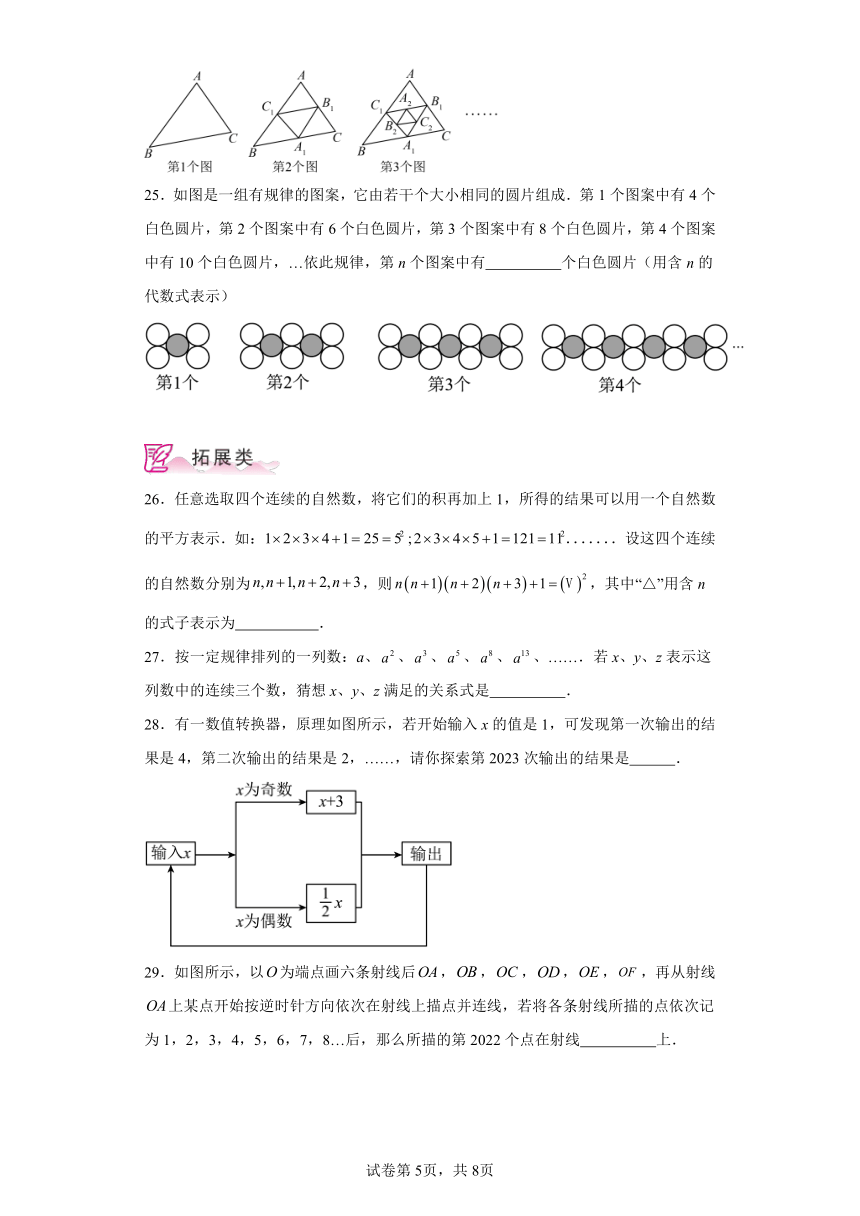
6.探索规律:观察下面的一列单项式:、、、、、…,根据其中的规律得出的第8个单项式是( )
A. B. C. D.
7.将一列有理数 ,,,,,,,按如图所示有序排列,各个“峰”中有理数的位置依次标注为 ,,,,.根据图中的排列规律可知,有理数 在“峰 ”中的 处.则有理数 在( )
A.“峰 ” 处 B.“峰 ” 处 C.“峰 ” 处 D.“峰 ” 处
8.我们把称为有理数的差倒数,如:2的差倒数是,的差倒数是.如果,是的差倒数,是的差倒数,是的差倒数,…,依此类推,那么的值是( )
A. B. C. D.1
9.如图,以一根火柴棍为一边,用火柴棍拼成一排由三角形组成的图形.如果图形中含有2021个三角形,需要( )火柴棍.
A.4045根 B.4042根 C.4043根 D.4041根
10.分形的概念是由数学家本华曼德博提出的,如图是分形的一种,第1个图案有2个三角形,第2个图案有4个三角形,第3个图案有8个三角形,第4个图案有16个三角形,…,按此规律分形得到第个图案中三角形的个数是( )
A. B. C. D.
11.依照以下图形变化的规律,则第125个图形中黑色正方形的数量是( )
A.187 B.188 C.189 D.190
12.如图,在第个白球的前面,黑球的个数总共有( )
A.个 B.个 C.个 D.个
13.在“点燃我的梦想,数学皆有可衡”数学创新设计活动中,“智多星”小强设计了一个数学探究活动:对依次排列的两个整式m,n按如下规律进行操作:
第1次操作后得到整式串m,n,;
第2次操作后得到整式串m,n,,;
第3次操作后…
其操作规则为:每次操作增加的项,都是用上一次操作得到的最末项减去其前一项的差,小强将这个活动命名为“回头差”游戏.
则该“回头差”游戏第2023次操作后得到的整式中各项之和是( )
A. B.m C. D.
14.一组按规律排列的式子:,,,那么第个式子是( )
A. B. C. D.
15.我国宋朝时期的数学家杨辉,曾将大小完全相同的圆柱形木桩逐层堆积,形成“三角垛”,顶层记为第1层,有1根圆木桩;前2层有3根圆木桩;前3层有6根圆木桩,往下依次是前4层、前5层……如图,给出了前4层.若用表示前n层的圆木桩数目,其中,2,3,…,则的值是( )
A. B. C. D.
二、填空题
16.定义:是不为的有理数,我们把称为的差倒数,如的差倒数是的差倒数是,已知是的差倒数,是的差倒数,是的差倒数,以此类推,则 .
17.有一组数依次为,,,…按此规律,第个数为 .(用含的代数式表示)
18.有一组数:1,0.8,,,……,按此规律第七个数是 .
19.用同样大小的黑色棋子按如图表示的方式摆图形,按照这样的规律摆下去,则第100个图形需棋子 枚.
20.观察下列图形:它们是按一定规律排列的,依此规律,第7个图形共有 个★
21.定义:若是不为1的有理数,则称为的差倒数.如2的差倒数为.现有若干个数,第一个数记为,是的差倒数,是的差倒数,依此类推,若,则 .
22.如图是一个运算程序的示意图,若开始输入的值为125,第1次输出的结果为25,再将25继续输入,……,则第2022次输出的结果为 .
23.在下面各正方形中的四个数之间都有一定的规律,根据此规律,m的值是 .
24.如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,…,依此类推,则第2023个图中共有 个三角形.
25.如图是一组有规律的图案,它由若干个大小相同的圆片组成.第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,…依此规律,第n个图案中有 个白色圆片(用含n的代数式表示)
26.任意选取四个连续的自然数,将它们的积再加上1,所得的结果可以用一个自然数的平方表示.如:.......设这四个连续的自然数分别为,则,其中“△”用含n的式子表示为 .
27.按一定规律排列的一列数:a、、、、、、…….若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是 .
28.有一数值转换器,原理如图所示,若开始输入x的值是1,可发现第一次输出的结果是4,第二次输出的结果是2,……,请你探索第2023次输出的结果是 .
29.如图所示,以为端点画六条射线后,,,,,,再从射线上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2022个点在射线 上.
30.如图,用灰、白两种颜色的正六边形镶嵌成若干图案,按照这种规律,第n个图案中白色正六边形的个数y与n之间的关系式为 .
三、解答题
31.假设有足够多的黑白围棋子,按照一定的规律排列成一行.第2019个棋子是黑色还是白色?
32.用棋子摆出下列一组图形:
(1)摆第1个图形用4枚棋子,摆第2个图形用8枚棋子,摆第3个图形用12枚棋子,那么摆第4个图形用______枚棋子;
(2)按照这种方式摆下去,摆第50个图形用______枚棋子.(均不用写出过程)
33.(1)
(2)
34.用同样规格的黑,白两种颜色的正方形瓷砖按如图所示的方式铺宽为米的小路.
(1)铺第6个图形用黑色正方形瓷砖 块,用白色正方形瓷砖 块;
(2)按照此方式铺下去,铺第n个图形用黑色正方形瓷砖 块,用白色正方形瓷砖 块(用含n的代数式表示);
(3)在(2)的基础上,若黑,白两种颜色的瓷砖规格都为(长为米×宽米),若按照此方式铺满一段总面积为平方米的小路时,n是多少?
35.观察下列三行数:
2,4,8,16,32,…;①
,,,,,…;②
0,2,6,14,30,…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第99个数,并求出这三个数的和.
36.背景阅读:意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:,,,,,,,,其中从第三个数起,每一个数都等于它前面两上数的和.为了纪念这个著名的发现,人们将这组数命名为斐波那契数列.
实践操作:
(1)写出斐波那契数列的前 个数;
(2)斐波那契数列的前个数中,有 个奇数?
(3)现以这组数中的各个数作为正方形的边长构造如图 的正方形系列:
再分别依次从左到右取 个、 个、 个、 个, 正方形拼成如图 长方形并记为①,②,③,④,⑤ .
(ⅰ)通过计算相应长方形的周长填写表(不计拼出的长方形内部的线段);
序号 ① ② ③ ④ ⑤ ……
周长 6 10 ……
(ⅱ)若按此规律继续拼成长方形,求序号为⑩的长方形的长与宽.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】观察得出规律,据此求出第n个数即可.
【详解】解:观察3,5,7,9,……,
每一个数都比前一个数大2,
则第n个数是,
故选D.
【点睛】题目主要考查列代数式,解题的关键是分析一列数找出规律,按规律求解.
2.B
【分析】当输入的是奇数时,用代数式计算;再循环输入,若是奇数,继续使用进行计算,若是偶然,使用进行计算;再将结果输入,进行判定,并计算,由此即可求解.
【详解】解:输入:,
第1次, ,
第2次,,
第3次,,
第4次,,
第5次,,
第6次,,
第7次,,
第8次,,
…
第次,,
∴第次输出的结果为,
故选:.
【点睛】本题主要考查程序图,掌握程序图执行条件,计算的代数式,有理数的混合法则是解题的关键.
3.A
【分析】观察不难发现,每4个数为一个循环组,个位数字依次循环,用2021÷3,根据商和余数的情况确定答案即可.
【详解】解:个位数字分别为3、9、7、1依次循环,
∵2021÷4=505余1,
∴32021的个位数字与循环组的第1个数的个位数字相同,是3.
故选A.
【点睛】本题考查了数字变化类规律的归纳能力,尾数特征,观察数据发现每4个数为一个循环组,个位数字依次循环是解题的关键.
4.B
【分析】仔细观察图形,找到图形中★个数的通项公式,然后代入求解即可.
【详解】解:∵第①个图形中共有个★,
第②个图形中共有个★,
第③个图形中共有个★,
…,
∴按此规律排列下去,第个图形中共有个★,
∴第⑥个图形中的★个数为,
故选:B.
【点睛】本题考查了图形的变化类问题,解题的关键是仔细的读题并找到图形变化的规律,难度不大.
5.D
【分析】观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,从而确定答案.
【详解】解:观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵,
∴滚动第2021次后与第一次相同,
∴朝下的数字是5的对面2,
故选:D.
【点睛】本题考查了正方体相对两个面上的文字及图形的变化类问题,解题的关键是发现规律.
6.C
【分析】根据系数与字母的指数规律即可求解.
【详解】解:观察系数可以发现后一项是前一项的倍,观察字母的指数可以发现为依次加1,
因此第8个单项式的系数为,字母部分为,
故选:C.
【点睛】本题考查了整式的规律题,解题关键是发现变化规律.
7.D
【分析】观察图形可知:相邻两峰相同位置的数的绝对值的差为5,结合,可得有理数2021在“峰404”中第5个位置上,即可求解.
【详解】解:观察图形可知:相邻两峰相同位置的数的绝对值的差为5,
∵,
∴有理数2021在“峰404”中第5个位置上,
即有理数2021在“峰404”中E的位置上;
故选:D.
【点睛】本题考查了规律探究,观察图形,得出各峰相同位置数之间的关系是解题的关键.
8.C
【分析】根据题意先写出前几个、、、……,找到规律求解即可.
【详解】解:根据题意,
,
,
……
由此发现,这列数以、、为一组,依次循环,
∵,
∴,
故选:C.
【点睛】本题考查数字类规律探究,理解题中新定义,找到数字变化规律是解答的关键.
9.C
【分析】根据已有图形,推断出相应的数字规律,进行求解即可.
【详解】解:由图可知:
1个三角形需要3根火柴棍;
2个三角形需要:根火柴棍;
3个三角形需要:根火柴棍;
4个三角形需要:根火柴棍;
,
个三角形需要:(根)火柴棍;
∴2021个三角形,需要根火柴棍;
故选C.
【点睛】本题考查图形类规律探究.根据已有图形,抽象概括出相应的数字规律,是解题的关键.
10.D
【分析】根据前面图案中三角形的个数,找出规律,即可求解.
【详解】解:第1个图案有2个三角形,即个;
第2个图案有4个三角形,即个;
第3个图案有8个二角形,即个;
第4个图案有16个三角形,即个;
则第个图案有个三角形,
只有D选项符合题意,
故选:D.
【点睛】此题考查了图形类规律的探索问题,解题的关键是根据前面的图案,找出相关规律,即可求解.
11.B
【分析】根据图形的变化寻找规律即可.
【详解】解:第1个图形中黑色正方形的数量是2,
第2个图形中黑色正方形的数量是3,
第3个图形中黑色正方形的数量是5,
发现规律:
当为偶数时,第个图形中黑色正方形的数量为:个,
当为奇数时,第个图形中黑色正方形的数量为:个.
第125个图形中黑色正方形的数量为:(个.
故选:B.
【点睛】本题考查了规律型图形的变化类,解决本题的关键是根据图形的变化寻找规律.
12.C
【分析】由图形可知,第个白球与第个白球之间的黑球的个数为:,第个白球与第个白球之间的黑球的个数为:,第个白球与第个白球之间的黑球的个数为:,,则第个白球与第个白球之间的黑球的个数为:,从而可求解.
【详解】解:第个白球与第个白球之间的黑球的个数为:,
第个白球与第个白球之间的黑球的个数为:,
第个白球与第个白球之间的黑球的个数为:,
,
第个白球与第个白球之间的黑球的个数为:,
在第个白球的前面,黑球的个数总共有:.
故选:C.
【点睛】本题主要考查图形的变化规律,解答的关键是由所给的图形总结出存在的规律.
13.D
【分析】先逐步分析前面5次操作,可得整式串每四次一循环,再求解第四次操作后所有的整式之和为:,结合,从而可得答案.
【详解】解:第1次操作后得到整式串m,n,;
第2次操作后得到整式串m,n,,;
第3次操作后得到整式串m,n,,,;
第4次操作后得到整式串m,n,,,,;
第5次操作后得到整式串m,n,,,,,;
归纳可得:以上整式串每六次一循环,
∵,
∴第2023次操作后得到的整式中各项之和与第1次操作后得到整式串之和相等,
∴这个和为,
故选D
【点睛】本题考查的是整式的加减运算,代数式的规律探究,掌握探究的方法,并总结概括规律并灵活运用是解本题的关键.
14.C
【分析】根据分子的变化得出分子变化的规律,根据分母的变化得出分母变化的规律,根据分数符号的变化规律得出分数符号的变化规律,即可得到该组式子的变化规律.
【详解】解:分子为,其指数为2,5,8,11,…其规律为,
分母为,其指数为1,2,3,4,…其规律为,
分数符号为,,,,,其规律为,
所以第个式子.
故选:C.
【点睛】此题考查了探索规律,先根据分子、分母的变化得出规律,再根据分式符号的变化得出规律是解题的关键.
15.A
【分析】先用含n的代数式表示出,即,再通过裂项相消法计算即可.
【详解】解:由题意知,,,……
因此,
故
,
故选:A.
【点睛】本题考查用代数式表示图形的规律,以及有理数的混合运算,解题的关键是用含n的代数式表示出,熟练运用裂项相消法.
16.##0.5
【分析】根据题目中的数据,求出这列数的前几项,从而发现数字的变化特点,然后根据变化特点即可得到的值.
【详解】解:由题意,得:
,
,
,
,
,
由此可得,这列数依次以循环出现,
,
,
故答案为:.
【点睛】本题考查数字的变化类、新定义,解答本题的关键是明确题意,发现出数字的变化特点,当不能从题干当中直接得到结果时,求出前面几项,然后再分析规律是答题过程中常用的一种技巧.
17.##
【分析】根据所给分数,分别找出分子分母的规律即可得出答案.
【详解】解:∵一组数依次为,,,…
∴第个数为,
故答案为:.
【点睛】本题考查数字类规律探索,找出规律是解题的关键.
18.
【分析】根据题目中的数据,可以发现数字的变化特点,从而可以写出第七个数.
【详解】解:∵1,0.8,,, ,…,
∴这组数可以写成, ,,,…,
∴第n个数为:,
∴第7个数为:=,
故答案为:.
【点睛】本题主要考查数字的变化规律,解答的关键是由所给的数字分析出存在的规律.
19.301
【分析】认真观察给出的第一个图,第二个图,第三个图,试猜想第个图,找到与点数的关系,再按照这个规律求出第100个图所需棋子枚数.
【详解】解:第一个图,点数4,
第二个图,点数,
第三个图,点数,
猜想
第四个图,点数,
第五个图,点数,
.
第个图,点数,
第100个图形需棋子:(枚.
故答案为:301.
【点睛】本题考查了图形变化,解题的关键是读懂题意,能发现变化中的规律,利用规律解决问题.
20.18
【分析】找出规律即可求得结果.
【详解】第1个图形有:个,
第2个图形有:个,
第3个图形有:个,
第4个图形有:个,
…,
则第7个图形有:个;
故答案为:18.
【点睛】本题考查了图形规律探索问题,关键是由特殊到一般得出规律.
21.
【分析】根据规定进行计算,得出:,,,发现3个一循环,按照这个规律计算即可.
【详解】∵,
∴,
,
由此可以看出,,,三个数不断循环出现.
因为,,
所以.
故答案为:.
【点睛】此题考查规律型:数字的变化类,关键是发现循环的规律,然后利用规律进行计算分析判断.
22.5
【分析】根据题意可以先求出前几次输出结果,发现规律:从第2次开始,5,1,5,1,…,每2次为一个循环,进而可得第2022次输出的结果与第2次输出的结果一样.
【详解】解:根据题意可知,
开始输入x的值是125,第1次输出的结果是25,
第2次输出的结果是5,
第3次输出的结果是1,
第4次输出的结果是5,
第5次输出的结果是1,
第6次输出的结果是5,
依次继续下去,
…,
发现规律,从第2次开始,5,1,5,1,…,每2次为一个循环,
∵,
∴第2022次输出的结果与第2次输出的结果一样是5.
故答案为:5.
【点睛】本题考查了求代数式的值,探索数字变化规律,关键能根据程序图求出结果,得出规律是解此题的关键.
23.65
【分析】观察前四个正方形规律是:左上、左下、右上三个数是连续的三个自然数,右下=左上×左下+右上,可得m的值.
【详解】解:由前四个正方形内数的规律可知:
每个正方形左上、左下、右上三个数是连续的三个自然数,
而每个正方形右下的数=左上的数×左下的数+右上的数,
故.
故答案为:65.
【点睛】本题考查数字的变化规律,培养学生观察、分析、归纳问题的能力,观察四个正方形得出规律解决问题,属中档题.
24.8089
【分析】根据图形中三角形的个数总结规律,根据规律即可得结论.
【详解】解:第1个图中有1个,即(个)三角形,
第2个图中共有5个,即(个)三角形,
第3个图中共有9个,即(个)三角形,
...,
所以第n个图中共有个三角形,
则第2023个图中共有(个).
故答案为:8089.
【点睛】本题考查的是图形的变化类的规律,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
25.
【分析】由于第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,,可得第个图案中有白色圆片的总数为.
【详解】解:第1个图案中有4个白色圆片,
第2个图案中有6个白色圆片,
第3个图案中有8个白色圆片,
第4个图案中有10个白色圆片,
,
∴第个图案中有个白色圆片.
故答案为:.
【点睛】此题考查图形的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.解题关键是总结归纳出图形的变化规律.
26.
【分析】根据所给等式归纳总结得到第n个算式即可.
【详解】解:∵,
,
,
...
∴,
∴“△”用含n的式子表示为,
故答案为:.
【点睛】此题考查了有理数的混合运算,数字类规律探索,弄清题中的规律是解本题的关键.
27.
【分析】首项判断出这列数中,a的指数各项依次为1,2,3,5,8,13,…,从第三个数起,每个数都是前两数之和;然后根据同底数的幂相乘,底数不变,指数相加,可得这列数中的连续三个数,满足,据此解答即可.
【详解】∵,…,
∴x、y、z满足的关系式是:.
故答案为:.
【点睛】此题考查数字的变化规律及同底数幂的乘法法则,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出x、y、z的指数的特征.
28.4
【分析】由题意知,第一次输出的结果是4,第二次输出的结果是2,第三次输出的结果是1,第四次输出的结果是4,第五次输出的结果是2,……,可知三次为一个循环,由,进而可得第2023次输出的结果.
【详解】解:由题意知,第一次输出的结果是4,第二次输出的结果是2,第三次输出的结果是1,第四次输出的结果是4,第五次输出的结果是2,……,
∴可知三次为一个循环,
∵,
∴第2023次输出的结果是4,
故答案为:4.
【点睛】本题考查了程序流程图与有理数计算,规律探究.解题的关键在于根据推导一般性规律.
29.
【分析】根据题意可得,1在射线上,2在射线上,3在射线上,4在射线上,5在射线上,6在射线上,7在射线上,…,每六个一循环.根据,即可求解.
【详解】解∶∵1在射线上,2在射线上,3在射线上,4在射线上,5在射线上,6在射线上,7在射线上,…
∴每六个一循环.
∵,
∴所描的第2022个点所在射线和6所在射线一样.
∴所描的第2022个点在射线上.
故答案为:
【点睛】本题考查了图形规律题,找到规律是解题的关键.
30.
【分析】根据题意:第1个图案中,白色的地砖有块;第2个图案中,白色的地砖有块;…根据发现的规律即可得答案.
【详解】解:第1个图案中,白色的地砖有块;
第2个图案中,白色的地砖有块;
第3个图案中,白色的地砖有块;
……
第n个图形中,白色的地砖有块.
故答案为:.
【点睛】此题主要考查了图形的变化规律,解决此类题首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
31.黑色
【分析】观察排成的一行黑白围棋子,不难发现,按白白黑黑白黑,这样6个为一个循环,那么用2019除以6看余几,即和第几个棋子一样.
【详解】解:由已知排成的一行黑白围棋子,得到:白白黑黑白黑 白白黑黑白黑 白白黑黑白黑…,这样6个为一个循环,
2019÷6=336……3,
因此第2019个棋子和第三个棋子颜色相同,为黑色.
【点睛】本题考查了图形变化类问题,解题的关键是找到图形规律,再通过计算得出答案.
32.(1)16
(2)200
【分析】根据前三个图的规律推断一般规律即可.
【详解】(1)解:∵第1个图形需要棋子的枚数为:4,
第2个图形需要棋子的枚数为:8=4×2,
第3个图形需要棋子的枚数为:12=4×3,
...,
∴第3个图形需要棋子的枚数为:4×4=16(枚),
故答案为:16;
(2)由(1)得:第n个图形需要棋子的枚数为:4n,
∴第50个图形需要棋子的枚数为:4×50=200(枚),
故答案为:200.
【点睛】本题考查图形类规律题,能通过图形推出一般规律是解题的关键.
33.,
【分析】(1)根据拆项公式,拆项后通过加减相互抵消即可简算;
(2)根据拆项公式,可推导出,拆项后提取再通过加减相互抵消即可简算.
【详解】
【点睛】本题考查乘法分配律,解题关键是掌握拆项公式,拆项后通过加减相互抵消即可简算.
34.(1)25,14
(2),
(3)16
【分析】(1)根据图形算出前几个图形中含有的瓷砖数,找到规律,再代入求解;
(2)由(1)的规律填空;
(3)根据瓷砖数乘一块瓷砖的面积等于总面积列方程求解.
【详解】(1)解:第1个图形中有个黑色正方形瓷砖,有个白色瓷砖;
第2个图形中有个黑色正方形瓷砖,有个白色瓷砖;
第3个图形中有个黑色正方形瓷砖,有个白色瓷砖;
,
第个图形中有个黑色正方形瓷砖,有个白色瓷砖;
第6个图形中有25个黑色正方形瓷砖,有14个白色瓷砖;
故答案为:25,14;
(2)由(1)知:第个图形中有个黑色正方形瓷砖,有个白色瓷砖,
故答案为:,;
(3)第个图形中有个黑色正方形瓷砖,有个白色瓷砖,
故第个图形中有个正方形瓷砖;
,
解得:.
【点睛】本题考查了图形的变换类,找到变化规律是解题的关键.
35.(1)第①行的数是按排列的
(2)第②行的数是第一行数的相反数,按排列的,
第③行的数是比第一行数少2,按排列的;
(3)
【分析】(1)根据已知数据都是2的乘方即可得到规律;
(2)根据第②行数据都是第①行数据的相反数,第③行数比第①行数少2可得规律;
(3)分别求出每行第99个数进而求出它们的和.
【详解】(1)解:2,4,8,16,32,…
第①行的数是按排列的;
(2)第②行的数是第一行数的相反数,按排列的,
第③行的数是比第一行数少2,按排列的;
(3)第①行的第99个数为,第②行的第99个数为,第③行的第99个数为,
所以 .
【点睛】本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,求出相应的数字.
36.(1),,,,,,,,,
(2)
(3)(ⅰ);;;(ⅱ)长为 ,宽为
【分析】(1)斐波那契数列的定义即可求解;
(2)分析婓波那契数列,可以发现每三项都是前两个为奇第三个为偶,结合2017是3的多少倍余几,即可得出结论;
(3)①根据图形特性,可以找出周长为最大的正方形的周长+小一号的正方形的两条边,代入数据即可得出结论;
②根据(1)中结果及规律即可得到序号为⑩的长方形长和宽.
【详解】(1)写出斐波那契数列的前10个数是:1,1,2,3,5,8,13,21,34,55
(2)奇偶特点:奇,奇,偶,奇,奇,偶,奇,奇,偶……,3个一周期.
奇数:(个),
故答案为:;
(3)(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号为①的长方形的周长为;
序号为②的长方形的周长为;
序号为③的长方形的周长为;
序号为④的长方形的周长为;
序号为⑤的长方形的周长为;
序号 ① ② ③ ④ ⑤ ……
周长 6 10 16 26 42 ……
(ii)由(1)得,第11个数为,
第10个长方形的长为:;宽为:.
【点睛】本题主要考查规律型—数字的变换类,根据已知找出正确的规律是解题关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.观察一组数据:3,5,7,9,……,那么第(是自然数)个数据是( )
A. B. C. D.
2.如图所示的运算程序中,若开始输入的值为,我们发现第次输出的结果为,第次输出的结果为,…第次输出的结果为( )
A. B. C. D.
3.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,…,通过观察,找出规律,确定32021的个位数字是( )
A.3 B.9 C.7 D.1
4.下列图形都是由同样大小的★按照一定规律组成的,其中第①个图形中共有个★,第②个图形中共有个★,第③个图形中共有个★,…,按此规律排列下去,第⑥个图形中的★个数为( )
A.个 B.个 C.个 D.个
5.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动算一次,则滚动第2021次后,骰子朝下一面的点数是( )
A.5 B.3 C.4 D.2
6.探索规律:观察下面的一列单项式:、、、、、…,根据其中的规律得出的第8个单项式是( )
A. B. C. D.
7.将一列有理数 ,,,,,,,按如图所示有序排列,各个“峰”中有理数的位置依次标注为 ,,,,.根据图中的排列规律可知,有理数 在“峰 ”中的 处.则有理数 在( )
A.“峰 ” 处 B.“峰 ” 处 C.“峰 ” 处 D.“峰 ” 处
8.我们把称为有理数的差倒数,如:2的差倒数是,的差倒数是.如果,是的差倒数,是的差倒数,是的差倒数,…,依此类推,那么的值是( )
A. B. C. D.1
9.如图,以一根火柴棍为一边,用火柴棍拼成一排由三角形组成的图形.如果图形中含有2021个三角形,需要( )火柴棍.
A.4045根 B.4042根 C.4043根 D.4041根
10.分形的概念是由数学家本华曼德博提出的,如图是分形的一种,第1个图案有2个三角形,第2个图案有4个三角形,第3个图案有8个三角形,第4个图案有16个三角形,…,按此规律分形得到第个图案中三角形的个数是( )
A. B. C. D.
11.依照以下图形变化的规律,则第125个图形中黑色正方形的数量是( )
A.187 B.188 C.189 D.190
12.如图,在第个白球的前面,黑球的个数总共有( )
A.个 B.个 C.个 D.个
13.在“点燃我的梦想,数学皆有可衡”数学创新设计活动中,“智多星”小强设计了一个数学探究活动:对依次排列的两个整式m,n按如下规律进行操作:
第1次操作后得到整式串m,n,;
第2次操作后得到整式串m,n,,;
第3次操作后…
其操作规则为:每次操作增加的项,都是用上一次操作得到的最末项减去其前一项的差,小强将这个活动命名为“回头差”游戏.
则该“回头差”游戏第2023次操作后得到的整式中各项之和是( )
A. B.m C. D.
14.一组按规律排列的式子:,,,那么第个式子是( )
A. B. C. D.
15.我国宋朝时期的数学家杨辉,曾将大小完全相同的圆柱形木桩逐层堆积,形成“三角垛”,顶层记为第1层,有1根圆木桩;前2层有3根圆木桩;前3层有6根圆木桩,往下依次是前4层、前5层……如图,给出了前4层.若用表示前n层的圆木桩数目,其中,2,3,…,则的值是( )
A. B. C. D.
二、填空题
16.定义:是不为的有理数,我们把称为的差倒数,如的差倒数是的差倒数是,已知是的差倒数,是的差倒数,是的差倒数,以此类推,则 .
17.有一组数依次为,,,…按此规律,第个数为 .(用含的代数式表示)
18.有一组数:1,0.8,,,……,按此规律第七个数是 .
19.用同样大小的黑色棋子按如图表示的方式摆图形,按照这样的规律摆下去,则第100个图形需棋子 枚.
20.观察下列图形:它们是按一定规律排列的,依此规律,第7个图形共有 个★
21.定义:若是不为1的有理数,则称为的差倒数.如2的差倒数为.现有若干个数,第一个数记为,是的差倒数,是的差倒数,依此类推,若,则 .
22.如图是一个运算程序的示意图,若开始输入的值为125,第1次输出的结果为25,再将25继续输入,……,则第2022次输出的结果为 .
23.在下面各正方形中的四个数之间都有一定的规律,根据此规律,m的值是 .
24.如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,…,依此类推,则第2023个图中共有 个三角形.
25.如图是一组有规律的图案,它由若干个大小相同的圆片组成.第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,…依此规律,第n个图案中有 个白色圆片(用含n的代数式表示)
26.任意选取四个连续的自然数,将它们的积再加上1,所得的结果可以用一个自然数的平方表示.如:.......设这四个连续的自然数分别为,则,其中“△”用含n的式子表示为 .
27.按一定规律排列的一列数:a、、、、、、…….若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是 .
28.有一数值转换器,原理如图所示,若开始输入x的值是1,可发现第一次输出的结果是4,第二次输出的结果是2,……,请你探索第2023次输出的结果是 .
29.如图所示,以为端点画六条射线后,,,,,,再从射线上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2022个点在射线 上.
30.如图,用灰、白两种颜色的正六边形镶嵌成若干图案,按照这种规律,第n个图案中白色正六边形的个数y与n之间的关系式为 .
三、解答题
31.假设有足够多的黑白围棋子,按照一定的规律排列成一行.第2019个棋子是黑色还是白色?
32.用棋子摆出下列一组图形:
(1)摆第1个图形用4枚棋子,摆第2个图形用8枚棋子,摆第3个图形用12枚棋子,那么摆第4个图形用______枚棋子;
(2)按照这种方式摆下去,摆第50个图形用______枚棋子.(均不用写出过程)
33.(1)
(2)
34.用同样规格的黑,白两种颜色的正方形瓷砖按如图所示的方式铺宽为米的小路.
(1)铺第6个图形用黑色正方形瓷砖 块,用白色正方形瓷砖 块;
(2)按照此方式铺下去,铺第n个图形用黑色正方形瓷砖 块,用白色正方形瓷砖 块(用含n的代数式表示);
(3)在(2)的基础上,若黑,白两种颜色的瓷砖规格都为(长为米×宽米),若按照此方式铺满一段总面积为平方米的小路时,n是多少?
35.观察下列三行数:
2,4,8,16,32,…;①
,,,,,…;②
0,2,6,14,30,…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第99个数,并求出这三个数的和.
36.背景阅读:意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:,,,,,,,,其中从第三个数起,每一个数都等于它前面两上数的和.为了纪念这个著名的发现,人们将这组数命名为斐波那契数列.
实践操作:
(1)写出斐波那契数列的前 个数;
(2)斐波那契数列的前个数中,有 个奇数?
(3)现以这组数中的各个数作为正方形的边长构造如图 的正方形系列:
再分别依次从左到右取 个、 个、 个、 个, 正方形拼成如图 长方形并记为①,②,③,④,⑤ .
(ⅰ)通过计算相应长方形的周长填写表(不计拼出的长方形内部的线段);
序号 ① ② ③ ④ ⑤ ……
周长 6 10 ……
(ⅱ)若按此规律继续拼成长方形,求序号为⑩的长方形的长与宽.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】观察得出规律,据此求出第n个数即可.
【详解】解:观察3,5,7,9,……,
每一个数都比前一个数大2,
则第n个数是,
故选D.
【点睛】题目主要考查列代数式,解题的关键是分析一列数找出规律,按规律求解.
2.B
【分析】当输入的是奇数时,用代数式计算;再循环输入,若是奇数,继续使用进行计算,若是偶然,使用进行计算;再将结果输入,进行判定,并计算,由此即可求解.
【详解】解:输入:,
第1次, ,
第2次,,
第3次,,
第4次,,
第5次,,
第6次,,
第7次,,
第8次,,
…
第次,,
∴第次输出的结果为,
故选:.
【点睛】本题主要考查程序图,掌握程序图执行条件,计算的代数式,有理数的混合法则是解题的关键.
3.A
【分析】观察不难发现,每4个数为一个循环组,个位数字依次循环,用2021÷3,根据商和余数的情况确定答案即可.
【详解】解:个位数字分别为3、9、7、1依次循环,
∵2021÷4=505余1,
∴32021的个位数字与循环组的第1个数的个位数字相同,是3.
故选A.
【点睛】本题考查了数字变化类规律的归纳能力,尾数特征,观察数据发现每4个数为一个循环组,个位数字依次循环是解题的关键.
4.B
【分析】仔细观察图形,找到图形中★个数的通项公式,然后代入求解即可.
【详解】解:∵第①个图形中共有个★,
第②个图形中共有个★,
第③个图形中共有个★,
…,
∴按此规律排列下去,第个图形中共有个★,
∴第⑥个图形中的★个数为,
故选:B.
【点睛】本题考查了图形的变化类问题,解题的关键是仔细的读题并找到图形变化的规律,难度不大.
5.D
【分析】观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,从而确定答案.
【详解】解:观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵,
∴滚动第2021次后与第一次相同,
∴朝下的数字是5的对面2,
故选:D.
【点睛】本题考查了正方体相对两个面上的文字及图形的变化类问题,解题的关键是发现规律.
6.C
【分析】根据系数与字母的指数规律即可求解.
【详解】解:观察系数可以发现后一项是前一项的倍,观察字母的指数可以发现为依次加1,
因此第8个单项式的系数为,字母部分为,
故选:C.
【点睛】本题考查了整式的规律题,解题关键是发现变化规律.
7.D
【分析】观察图形可知:相邻两峰相同位置的数的绝对值的差为5,结合,可得有理数2021在“峰404”中第5个位置上,即可求解.
【详解】解:观察图形可知:相邻两峰相同位置的数的绝对值的差为5,
∵,
∴有理数2021在“峰404”中第5个位置上,
即有理数2021在“峰404”中E的位置上;
故选:D.
【点睛】本题考查了规律探究,观察图形,得出各峰相同位置数之间的关系是解题的关键.
8.C
【分析】根据题意先写出前几个、、、……,找到规律求解即可.
【详解】解:根据题意,
,
,
……
由此发现,这列数以、、为一组,依次循环,
∵,
∴,
故选:C.
【点睛】本题考查数字类规律探究,理解题中新定义,找到数字变化规律是解答的关键.
9.C
【分析】根据已有图形,推断出相应的数字规律,进行求解即可.
【详解】解:由图可知:
1个三角形需要3根火柴棍;
2个三角形需要:根火柴棍;
3个三角形需要:根火柴棍;
4个三角形需要:根火柴棍;
,
个三角形需要:(根)火柴棍;
∴2021个三角形,需要根火柴棍;
故选C.
【点睛】本题考查图形类规律探究.根据已有图形,抽象概括出相应的数字规律,是解题的关键.
10.D
【分析】根据前面图案中三角形的个数,找出规律,即可求解.
【详解】解:第1个图案有2个三角形,即个;
第2个图案有4个三角形,即个;
第3个图案有8个二角形,即个;
第4个图案有16个三角形,即个;
则第个图案有个三角形,
只有D选项符合题意,
故选:D.
【点睛】此题考查了图形类规律的探索问题,解题的关键是根据前面的图案,找出相关规律,即可求解.
11.B
【分析】根据图形的变化寻找规律即可.
【详解】解:第1个图形中黑色正方形的数量是2,
第2个图形中黑色正方形的数量是3,
第3个图形中黑色正方形的数量是5,
发现规律:
当为偶数时,第个图形中黑色正方形的数量为:个,
当为奇数时,第个图形中黑色正方形的数量为:个.
第125个图形中黑色正方形的数量为:(个.
故选:B.
【点睛】本题考查了规律型图形的变化类,解决本题的关键是根据图形的变化寻找规律.
12.C
【分析】由图形可知,第个白球与第个白球之间的黑球的个数为:,第个白球与第个白球之间的黑球的个数为:,第个白球与第个白球之间的黑球的个数为:,,则第个白球与第个白球之间的黑球的个数为:,从而可求解.
【详解】解:第个白球与第个白球之间的黑球的个数为:,
第个白球与第个白球之间的黑球的个数为:,
第个白球与第个白球之间的黑球的个数为:,
,
第个白球与第个白球之间的黑球的个数为:,
在第个白球的前面,黑球的个数总共有:.
故选:C.
【点睛】本题主要考查图形的变化规律,解答的关键是由所给的图形总结出存在的规律.
13.D
【分析】先逐步分析前面5次操作,可得整式串每四次一循环,再求解第四次操作后所有的整式之和为:,结合,从而可得答案.
【详解】解:第1次操作后得到整式串m,n,;
第2次操作后得到整式串m,n,,;
第3次操作后得到整式串m,n,,,;
第4次操作后得到整式串m,n,,,,;
第5次操作后得到整式串m,n,,,,,;
归纳可得:以上整式串每六次一循环,
∵,
∴第2023次操作后得到的整式中各项之和与第1次操作后得到整式串之和相等,
∴这个和为,
故选D
【点睛】本题考查的是整式的加减运算,代数式的规律探究,掌握探究的方法,并总结概括规律并灵活运用是解本题的关键.
14.C
【分析】根据分子的变化得出分子变化的规律,根据分母的变化得出分母变化的规律,根据分数符号的变化规律得出分数符号的变化规律,即可得到该组式子的变化规律.
【详解】解:分子为,其指数为2,5,8,11,…其规律为,
分母为,其指数为1,2,3,4,…其规律为,
分数符号为,,,,,其规律为,
所以第个式子.
故选:C.
【点睛】此题考查了探索规律,先根据分子、分母的变化得出规律,再根据分式符号的变化得出规律是解题的关键.
15.A
【分析】先用含n的代数式表示出,即,再通过裂项相消法计算即可.
【详解】解:由题意知,,,……
因此,
故
,
故选:A.
【点睛】本题考查用代数式表示图形的规律,以及有理数的混合运算,解题的关键是用含n的代数式表示出,熟练运用裂项相消法.
16.##0.5
【分析】根据题目中的数据,求出这列数的前几项,从而发现数字的变化特点,然后根据变化特点即可得到的值.
【详解】解:由题意,得:
,
,
,
,
,
由此可得,这列数依次以循环出现,
,
,
故答案为:.
【点睛】本题考查数字的变化类、新定义,解答本题的关键是明确题意,发现出数字的变化特点,当不能从题干当中直接得到结果时,求出前面几项,然后再分析规律是答题过程中常用的一种技巧.
17.##
【分析】根据所给分数,分别找出分子分母的规律即可得出答案.
【详解】解:∵一组数依次为,,,…
∴第个数为,
故答案为:.
【点睛】本题考查数字类规律探索,找出规律是解题的关键.
18.
【分析】根据题目中的数据,可以发现数字的变化特点,从而可以写出第七个数.
【详解】解:∵1,0.8,,, ,…,
∴这组数可以写成, ,,,…,
∴第n个数为:,
∴第7个数为:=,
故答案为:.
【点睛】本题主要考查数字的变化规律,解答的关键是由所给的数字分析出存在的规律.
19.301
【分析】认真观察给出的第一个图,第二个图,第三个图,试猜想第个图,找到与点数的关系,再按照这个规律求出第100个图所需棋子枚数.
【详解】解:第一个图,点数4,
第二个图,点数,
第三个图,点数,
猜想
第四个图,点数,
第五个图,点数,
.
第个图,点数,
第100个图形需棋子:(枚.
故答案为:301.
【点睛】本题考查了图形变化,解题的关键是读懂题意,能发现变化中的规律,利用规律解决问题.
20.18
【分析】找出规律即可求得结果.
【详解】第1个图形有:个,
第2个图形有:个,
第3个图形有:个,
第4个图形有:个,
…,
则第7个图形有:个;
故答案为:18.
【点睛】本题考查了图形规律探索问题,关键是由特殊到一般得出规律.
21.
【分析】根据规定进行计算,得出:,,,发现3个一循环,按照这个规律计算即可.
【详解】∵,
∴,
,
由此可以看出,,,三个数不断循环出现.
因为,,
所以.
故答案为:.
【点睛】此题考查规律型:数字的变化类,关键是发现循环的规律,然后利用规律进行计算分析判断.
22.5
【分析】根据题意可以先求出前几次输出结果,发现规律:从第2次开始,5,1,5,1,…,每2次为一个循环,进而可得第2022次输出的结果与第2次输出的结果一样.
【详解】解:根据题意可知,
开始输入x的值是125,第1次输出的结果是25,
第2次输出的结果是5,
第3次输出的结果是1,
第4次输出的结果是5,
第5次输出的结果是1,
第6次输出的结果是5,
依次继续下去,
…,
发现规律,从第2次开始,5,1,5,1,…,每2次为一个循环,
∵,
∴第2022次输出的结果与第2次输出的结果一样是5.
故答案为:5.
【点睛】本题考查了求代数式的值,探索数字变化规律,关键能根据程序图求出结果,得出规律是解此题的关键.
23.65
【分析】观察前四个正方形规律是:左上、左下、右上三个数是连续的三个自然数,右下=左上×左下+右上,可得m的值.
【详解】解:由前四个正方形内数的规律可知:
每个正方形左上、左下、右上三个数是连续的三个自然数,
而每个正方形右下的数=左上的数×左下的数+右上的数,
故.
故答案为:65.
【点睛】本题考查数字的变化规律,培养学生观察、分析、归纳问题的能力,观察四个正方形得出规律解决问题,属中档题.
24.8089
【分析】根据图形中三角形的个数总结规律,根据规律即可得结论.
【详解】解:第1个图中有1个,即(个)三角形,
第2个图中共有5个,即(个)三角形,
第3个图中共有9个,即(个)三角形,
...,
所以第n个图中共有个三角形,
则第2023个图中共有(个).
故答案为:8089.
【点睛】本题考查的是图形的变化类的规律,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
25.
【分析】由于第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,,可得第个图案中有白色圆片的总数为.
【详解】解:第1个图案中有4个白色圆片,
第2个图案中有6个白色圆片,
第3个图案中有8个白色圆片,
第4个图案中有10个白色圆片,
,
∴第个图案中有个白色圆片.
故答案为:.
【点睛】此题考查图形的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.解题关键是总结归纳出图形的变化规律.
26.
【分析】根据所给等式归纳总结得到第n个算式即可.
【详解】解:∵,
,
,
...
∴,
∴“△”用含n的式子表示为,
故答案为:.
【点睛】此题考查了有理数的混合运算,数字类规律探索,弄清题中的规律是解本题的关键.
27.
【分析】首项判断出这列数中,a的指数各项依次为1,2,3,5,8,13,…,从第三个数起,每个数都是前两数之和;然后根据同底数的幂相乘,底数不变,指数相加,可得这列数中的连续三个数,满足,据此解答即可.
【详解】∵,…,
∴x、y、z满足的关系式是:.
故答案为:.
【点睛】此题考查数字的变化规律及同底数幂的乘法法则,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出x、y、z的指数的特征.
28.4
【分析】由题意知,第一次输出的结果是4,第二次输出的结果是2,第三次输出的结果是1,第四次输出的结果是4,第五次输出的结果是2,……,可知三次为一个循环,由,进而可得第2023次输出的结果.
【详解】解:由题意知,第一次输出的结果是4,第二次输出的结果是2,第三次输出的结果是1,第四次输出的结果是4,第五次输出的结果是2,……,
∴可知三次为一个循环,
∵,
∴第2023次输出的结果是4,
故答案为:4.
【点睛】本题考查了程序流程图与有理数计算,规律探究.解题的关键在于根据推导一般性规律.
29.
【分析】根据题意可得,1在射线上,2在射线上,3在射线上,4在射线上,5在射线上,6在射线上,7在射线上,…,每六个一循环.根据,即可求解.
【详解】解∶∵1在射线上,2在射线上,3在射线上,4在射线上,5在射线上,6在射线上,7在射线上,…
∴每六个一循环.
∵,
∴所描的第2022个点所在射线和6所在射线一样.
∴所描的第2022个点在射线上.
故答案为:
【点睛】本题考查了图形规律题,找到规律是解题的关键.
30.
【分析】根据题意:第1个图案中,白色的地砖有块;第2个图案中,白色的地砖有块;…根据发现的规律即可得答案.
【详解】解:第1个图案中,白色的地砖有块;
第2个图案中,白色的地砖有块;
第3个图案中,白色的地砖有块;
……
第n个图形中,白色的地砖有块.
故答案为:.
【点睛】此题主要考查了图形的变化规律,解决此类题首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
31.黑色
【分析】观察排成的一行黑白围棋子,不难发现,按白白黑黑白黑,这样6个为一个循环,那么用2019除以6看余几,即和第几个棋子一样.
【详解】解:由已知排成的一行黑白围棋子,得到:白白黑黑白黑 白白黑黑白黑 白白黑黑白黑…,这样6个为一个循环,
2019÷6=336……3,
因此第2019个棋子和第三个棋子颜色相同,为黑色.
【点睛】本题考查了图形变化类问题,解题的关键是找到图形规律,再通过计算得出答案.
32.(1)16
(2)200
【分析】根据前三个图的规律推断一般规律即可.
【详解】(1)解:∵第1个图形需要棋子的枚数为:4,
第2个图形需要棋子的枚数为:8=4×2,
第3个图形需要棋子的枚数为:12=4×3,
...,
∴第3个图形需要棋子的枚数为:4×4=16(枚),
故答案为:16;
(2)由(1)得:第n个图形需要棋子的枚数为:4n,
∴第50个图形需要棋子的枚数为:4×50=200(枚),
故答案为:200.
【点睛】本题考查图形类规律题,能通过图形推出一般规律是解题的关键.
33.,
【分析】(1)根据拆项公式,拆项后通过加减相互抵消即可简算;
(2)根据拆项公式,可推导出,拆项后提取再通过加减相互抵消即可简算.
【详解】
【点睛】本题考查乘法分配律,解题关键是掌握拆项公式,拆项后通过加减相互抵消即可简算.
34.(1)25,14
(2),
(3)16
【分析】(1)根据图形算出前几个图形中含有的瓷砖数,找到规律,再代入求解;
(2)由(1)的规律填空;
(3)根据瓷砖数乘一块瓷砖的面积等于总面积列方程求解.
【详解】(1)解:第1个图形中有个黑色正方形瓷砖,有个白色瓷砖;
第2个图形中有个黑色正方形瓷砖,有个白色瓷砖;
第3个图形中有个黑色正方形瓷砖,有个白色瓷砖;
,
第个图形中有个黑色正方形瓷砖,有个白色瓷砖;
第6个图形中有25个黑色正方形瓷砖,有14个白色瓷砖;
故答案为:25,14;
(2)由(1)知:第个图形中有个黑色正方形瓷砖,有个白色瓷砖,
故答案为:,;
(3)第个图形中有个黑色正方形瓷砖,有个白色瓷砖,
故第个图形中有个正方形瓷砖;
,
解得:.
【点睛】本题考查了图形的变换类,找到变化规律是解题的关键.
35.(1)第①行的数是按排列的
(2)第②行的数是第一行数的相反数,按排列的,
第③行的数是比第一行数少2,按排列的;
(3)
【分析】(1)根据已知数据都是2的乘方即可得到规律;
(2)根据第②行数据都是第①行数据的相反数,第③行数比第①行数少2可得规律;
(3)分别求出每行第99个数进而求出它们的和.
【详解】(1)解:2,4,8,16,32,…
第①行的数是按排列的;
(2)第②行的数是第一行数的相反数,按排列的,
第③行的数是比第一行数少2,按排列的;
(3)第①行的第99个数为,第②行的第99个数为,第③行的第99个数为,
所以 .
【点睛】本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,求出相应的数字.
36.(1),,,,,,,,,
(2)
(3)(ⅰ);;;(ⅱ)长为 ,宽为
【分析】(1)斐波那契数列的定义即可求解;
(2)分析婓波那契数列,可以发现每三项都是前两个为奇第三个为偶,结合2017是3的多少倍余几,即可得出结论;
(3)①根据图形特性,可以找出周长为最大的正方形的周长+小一号的正方形的两条边,代入数据即可得出结论;
②根据(1)中结果及规律即可得到序号为⑩的长方形长和宽.
【详解】(1)写出斐波那契数列的前10个数是:1,1,2,3,5,8,13,21,34,55
(2)奇偶特点:奇,奇,偶,奇,奇,偶,奇,奇,偶……,3个一周期.
奇数:(个),
故答案为:;
(3)(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号为①的长方形的周长为;
序号为②的长方形的周长为;
序号为③的长方形的周长为;
序号为④的长方形的周长为;
序号为⑤的长方形的周长为;
序号 ① ② ③ ④ ⑤ ……
周长 6 10 16 26 42 ……
(ii)由(1)得,第11个数为,
第10个长方形的长为:;宽为:.
【点睛】本题主要考查规律型—数字的变换类,根据已知找出正确的规律是解题关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
