24.1.4圆周角 同步练习题 人教版九年级数学上册(含答案)
文档属性
| 名称 | 24.1.4圆周角 同步练习题 人教版九年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 976.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 16:19:48 | ||
图片预览



文档简介
2023-2024学年人教版九年级数学上册《24.1.4圆周角》同步练习题(附答案)
一.选择题
1.如图,在⊙O中,AB=AC,若∠ABC=65°,则∠BOC的度数为( )
A.130° B.100° C.120° D.110°
2.如图,点A,B,C在⊙O上,若∠C=30°,则∠ABO的度数为( )
A.30° B.45° C.60° D.90°
3.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为( )
A.120° B.130° C.140° D.150°
4.如图,点A,B,C,在⊙O上,∠C=40°.则∠AOB的度数是( )
A.50° B.60° C.70° D.80°
5.如图,在⊙O中,弦BC与半径OA交于点D,若∠AOB=80°,∠A=60°,则∠ADB的度数为( )
A.100° B.110° C.120° D.90°
6.如图,△ABC的顶点A、B、C均在⊙O上,连接OA,OC,若∠ABC+∠AOC=75°,则∠OAC的度数是( )
A.45° B.50° C.60° D.65°
7.如图,在⊙O中,点C是上一点,若∠AOB=126°,则∠C的度数为( )
A.127° B.117° C.63° D.54°
8.如图所示,已知⊙O中,弦AB的长为10cm,测得圆周角∠ACB=45°,则直径AD为( )
A.5cm B.10cm C.15cm D.20cm
二.填空题
9.如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是 .
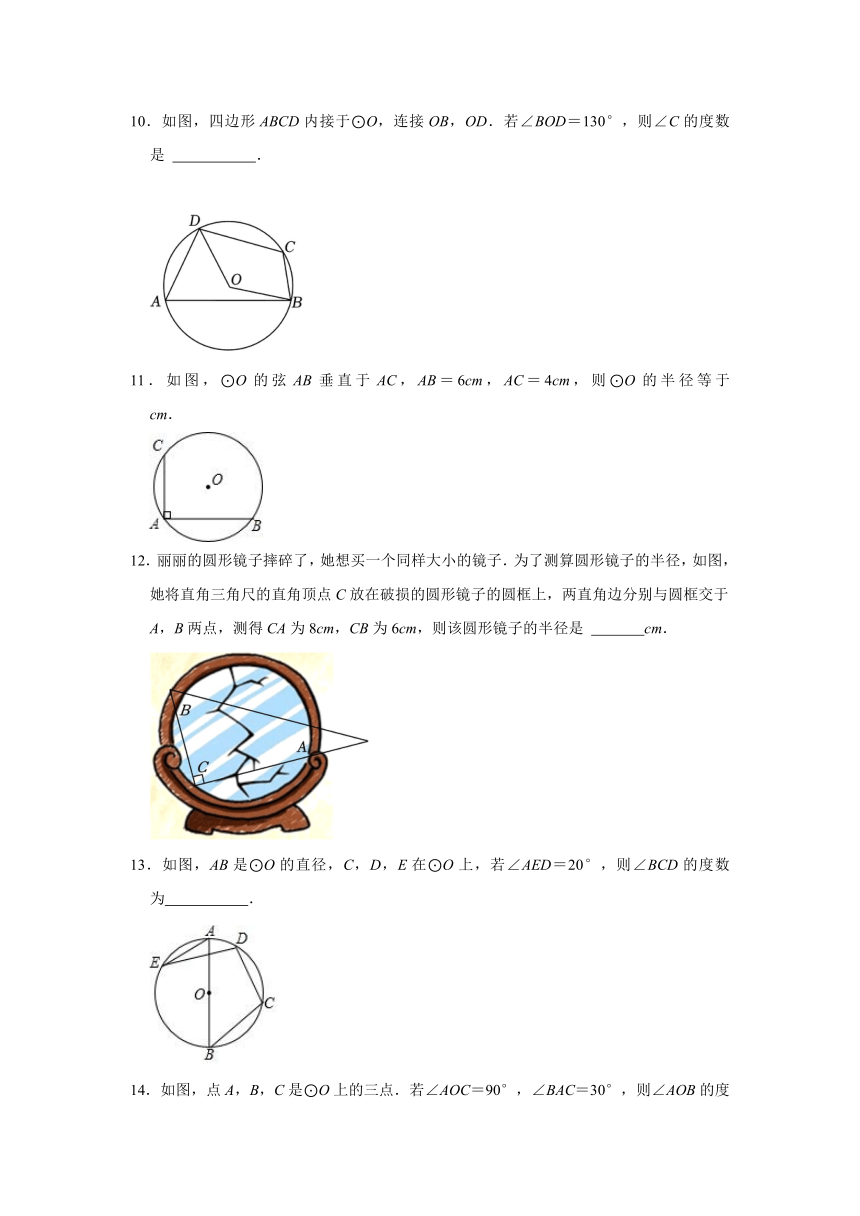
10.如图,四边形ABCD内接于⊙O,连接OB,OD.若∠BOD=130°,则∠C的度数是 .
11.如图,⊙O的弦AB垂直于AC,AB=6cm,AC=4cm,则⊙O的半径等于 cm.
12.丽丽的圆形镜子摔碎了,她想买一个同样大小的镜子.为了测算圆形镜子的半径,如图,她将直角三角尺的直角顶点C放在破损的圆形镜子的圆框上,两直角边分别与圆框交于A,B两点,测得CA为8cm,CB为6cm,则该圆形镜子的半径是 cm.
13.如图,AB是⊙O的直径,C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为 .
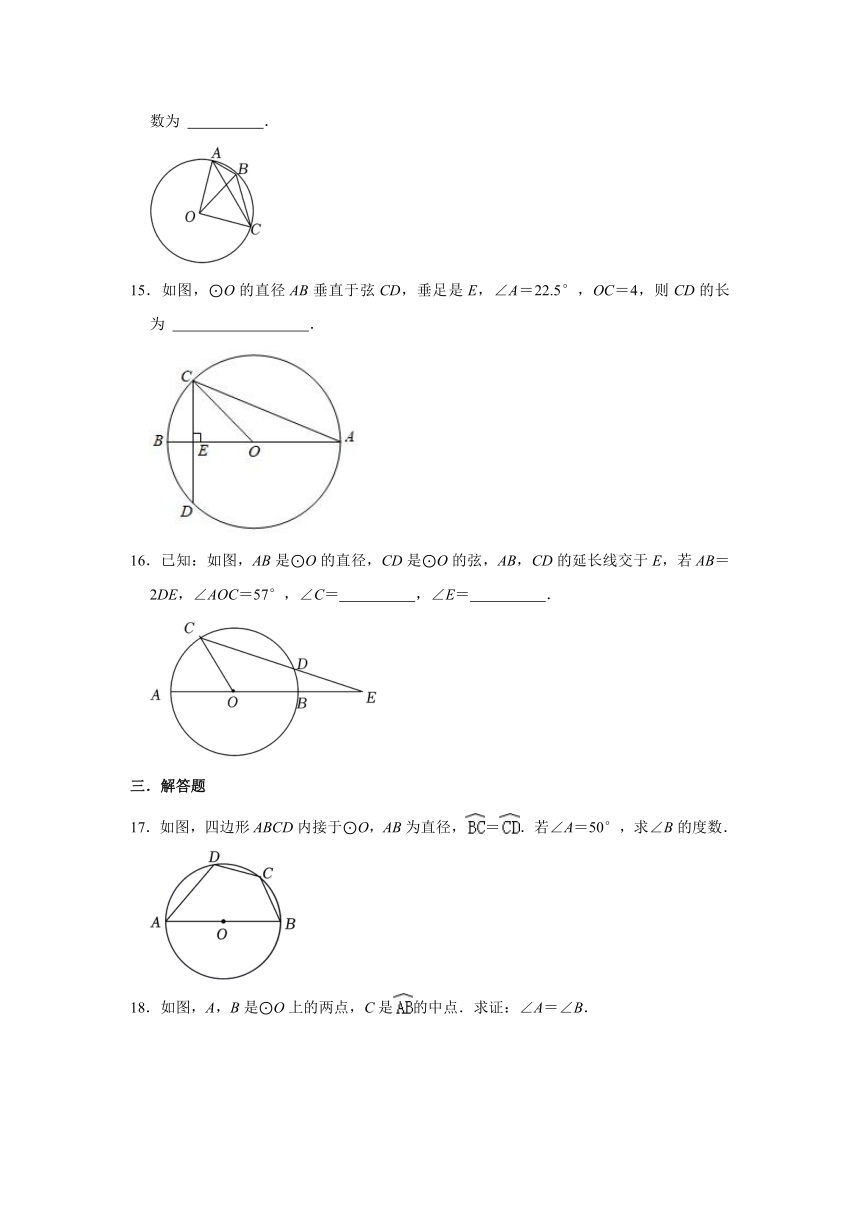
14.如图,点A,B,C是⊙O上的三点.若∠AOC=90°,∠BAC=30°,则∠AOB的度数为 .
15.如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为 .
16.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠AOC=57°,∠C= ,∠E= .
三.解答题
17.如图,四边形ABCD内接于⊙O,AB为直径,=.若∠A=50°,求∠B的度数.
18.如图,A,B是⊙O上的两点,C是的中点.求证:∠A=∠B.
19.如图,AB是⊙O直径,弦CD与AB相交于点E,∠ADC=26°.求∠CAB的度数.
20.在证明圆周角定理时,某学习小组讨论出圆心与圆周角有三种不同的位置关系(如图1,2,3所示),小敏说:当圆心O在∠ACB的边上时,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.小亮说:当圆心O在∠ACB的内部或外部时,可以通过添加直径这条辅助线,把问题转化为圆心O在∠ACB的边上时的特殊情形来解决.请选择图2或图3中的一种,完成证明.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半. 已知:如图,在⊙O中,所对的圆周角是∠ACB,圆心角是∠AOB. 求证:∠ACB=∠AOB.
21.如图,AB是⊙O的直径,点C在⊙O上,D是中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整.
解:在⊙O中,
∵D是的中点
∴=,
∴∠1=∠2( )(填推理的依据)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径,
∴∠ADB=90°( )(填推理的依据)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上,
∴∠C+∠B=180°( )(填推理的依据)
∴∠C=180°﹣∠B= (填计算结果)
22.如图,AB为⊙O的直径,弦CD⊥AB于点E,连接BC.若AB=6,∠B=30°,求:弦CD的长.
23.如图,AB=AC,AB是直径,求证:BC=2DE.
24.如图,割线PB与⊙O交于点A,B,割线PC过圆心O,且∠CPB=30°.若PC=13,⊙O的半径OA=5,求弦AB的长.
25.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若BE=8cm,CD=6cm,求⊙O的半径.
参考答案
一.选择题
1.解:∵AB=AC,∠ABC=65°,
∴∠ACB=∠ABC=65°,
∴∠A=180°﹣∠ABC﹣∠ACB=50°,
∴由圆周角定理得:∠BOC=2∠A=100°,
故选:B.
2.解:∵∠C=30°,
∴∠AOB=2∠C=60°,
∵OA=OB,
∴∠ABO=∠BAO=×(180°﹣∠AOB)=60°,
故选:C.
3.解:∵AB是直径,
∴∠ACB=90°,
∵∠ABC=50°,
∴∠A=90°﹣50°=40°,
∴∠BDC的度数为:180°﹣40°=140°
故选:C.
4.解:∵∠C=∠AOB,∠C=40°,
∴∠AOB=80°.
故选:D.
5.解:∵∠ACB=∠AOB=×80°=40°,
∴∠ADB=∠A+∠ACB=60°+40°=100°.
故选:A.
6.解:∵∠ABC=∠AOC,∠ABC+∠AOC=75°,
∴∠AOC+∠AOC=75°,
∴∠AOC=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:D.
7.解:如图:作圆周角∠ADB,使D在优弧上,
∵∠AOB=126°,
∴∠D=∠AOB=63°,
∵∠ACB+∠D=180°,
∴∠ACB=180°﹣63°=117°,
故选:B.
8.解:连接BD,如图,
∵AD为直径,
∴∠ABD=90°,
∵∠ADB=∠ACB=45°,
∴△ABD为等腰直角三角形,
∴AD=AB,
∵AB的长为10cm,
∴AD=10(cm),
故选:B.
二.填空题
9.解:∵AB是△ABC外接圆的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠A=90°﹣35°=55°.
故答案为55°.
10.解:∵∠BOD=2∠A,∠BOD=130°,
∴∠A=65°,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠C=115°,
故答案为:115°.
11.解:连接BC,
∵AB⊥AC,
∴∠BAC=90°,
∴BC是⊙O的直径,
∵AB=6cm,AC=4cm,
∴BC==2(cm),
∴⊙O的半径为:cm.
故答案为:.
12.解:如图,连接AB,
∵∠ACB=90°,
∴AB为圆形镜子的直径,
∵CA=8cm,CB=6cm,
∴AB===10(cm),
∴圆形镜子的半径为×10=5(cm),
故答案为:5.
13.解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AED=20°,
∴∠ACD=20°,
∴∠BCD=∠ACB+∠ACD=110°,
故答案为:110°.
14.解:∵∠BAC与∠BOC所对弧为,
由圆周角定理可知:∠BOC=2∠BAC=60°,
又∵∠AOC=90°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°.
故答案为:30°.
15.解:∵AB⊥CD,
∴CE=DE,∠OEC=90°,
∵∠BOC=2∠A=2×22.5°=45°,
∴△OCE为等腰直角三角形,
∴CE=OE=OC=2,
∴CD=2CE=4.
故答案为:4.
16.解:连接OD,
设∠E=x°,
∵AB=2DE,OA=OB=OD,
∴OD=DE,
∴∠E=∠DOE=x°,
∴∠CDO=∠E+∠DOE=2x°,
∵OC=OD,
∴∠C=∠CDO=2x°,
∵∠AOC=57°,∠AOC=∠E+∠C,
∴57=x+2x,
解得:x=19,
即∠E=19°,∠C=38°,
故答案为:38°,19°.
三.解答题
17.解:如图,连接AC.
∵=,∠BAD=50°,
∴∠BAC=∠DAC=∠BAD=×50°=25°,
∵AB为直径,
∴∠ACB=90°,
∴∠∠B=90°﹣∠BAC=90°﹣25°=65°.
18.证明:连接OC.
∵C是的中点,
∴,
∴∠AOC=∠BOC,
在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS),
∴∠A=∠B.
19.解:连接BC,
∵AB是⊙O直径,
∴∠ACB=90°,
∵∠B=∠D=26°,
∴∠CAB=90°﹣26°=64°.
20.证明:如图2:
∵OA=OC,
∴∠A=∠ACO,
∵∠AOD=∠A+∠ACO,
∴∠AOD=2∠ACO,
同理可得:∠BOD=2∠BCO,
∴∠AOB=∠AOD+∠BOD
=2∠ACO+2∠BCO
=2∠ACB,
∴∠ACB=∠AOB;
如图3:∵OA=OC,
∴∠A=∠ACO,
∵∠AOD=∠A+∠ACO,
∴∠AOD=2∠ACO,
同理可得:∠BOD=2∠BCO,
∴∠AOB=∠BOD﹣∠AOD
=2∠BCO﹣2∠ACO
=2∠ACB,
∴∠ACB=∠AOB.
21.解:在⊙O中,
∵D是的中点
∴=,
∴∠1=∠2(等弧所对的圆周角相等)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上,
∴∠C+∠B=180°(圆内接四边形的对角互补)
∴∠C=180°﹣∠B=125°
故答案为:等弧所对的圆周角相等,直径所对的圆周角是直角,圆内接四边形的对角互补,125°.
解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°
又AB=6,∠CBA=30°
∴AC=3,∠CAE=60°
∵弦CD⊥AB,AB为⊙O的直径
∴CE=ED
∵Rt△CEA中,CE=,
∴CD=2CE=3.
23.证明:连接AD、DE
∵AB为⊙O的直径
∴∠ADB=90°
∴AD⊥BC
∵AB=AC
∴∠BAD=∠DAC; BC=2BD=2DC
由圆周角定理可知:BD=DE
∴BC=2DE.
24.解:作OH⊥AB于H,
∴AH=BH,
∵PC=13,⊙O的半径OA=OC=5,
∴PO=PC﹣OC=13﹣5=8,
∵∠CPB=30°,
∴OH=PO=4,
∵AH2=AO2﹣OH2,
∴AH2=52﹣42,
∴AH=3,
∴AB=2AH=6.
25.(1)证明:∵OB=OC,
∴∠BCO=∠B,
∵∠B=∠D,
∴∠BCO=∠D;
(2)解:∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=CD=×6=3cm,
∴∠COE=90°,
设⊙O的半径为rcm,则OE=(8﹣r)cm,
在Rt△OCE中,根据勾股定理得:
r2﹣(8﹣r)2=32,
解得r=,
∴⊙O的半径为cm.
一.选择题
1.如图,在⊙O中,AB=AC,若∠ABC=65°,则∠BOC的度数为( )
A.130° B.100° C.120° D.110°
2.如图,点A,B,C在⊙O上,若∠C=30°,则∠ABO的度数为( )
A.30° B.45° C.60° D.90°
3.如图,AB是半圆O的直径,点C,D在半圆O上.若∠ABC=50°,则∠BDC的度数为( )
A.120° B.130° C.140° D.150°
4.如图,点A,B,C,在⊙O上,∠C=40°.则∠AOB的度数是( )
A.50° B.60° C.70° D.80°
5.如图,在⊙O中,弦BC与半径OA交于点D,若∠AOB=80°,∠A=60°,则∠ADB的度数为( )
A.100° B.110° C.120° D.90°
6.如图,△ABC的顶点A、B、C均在⊙O上,连接OA,OC,若∠ABC+∠AOC=75°,则∠OAC的度数是( )
A.45° B.50° C.60° D.65°
7.如图,在⊙O中,点C是上一点,若∠AOB=126°,则∠C的度数为( )
A.127° B.117° C.63° D.54°
8.如图所示,已知⊙O中,弦AB的长为10cm,测得圆周角∠ACB=45°,则直径AD为( )
A.5cm B.10cm C.15cm D.20cm
二.填空题
9.如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是 .
10.如图,四边形ABCD内接于⊙O,连接OB,OD.若∠BOD=130°,则∠C的度数是 .
11.如图,⊙O的弦AB垂直于AC,AB=6cm,AC=4cm,则⊙O的半径等于 cm.
12.丽丽的圆形镜子摔碎了,她想买一个同样大小的镜子.为了测算圆形镜子的半径,如图,她将直角三角尺的直角顶点C放在破损的圆形镜子的圆框上,两直角边分别与圆框交于A,B两点,测得CA为8cm,CB为6cm,则该圆形镜子的半径是 cm.
13.如图,AB是⊙O的直径,C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为 .
14.如图,点A,B,C是⊙O上的三点.若∠AOC=90°,∠BAC=30°,则∠AOB的度数为 .
15.如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为 .
16.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠AOC=57°,∠C= ,∠E= .
三.解答题
17.如图,四边形ABCD内接于⊙O,AB为直径,=.若∠A=50°,求∠B的度数.
18.如图,A,B是⊙O上的两点,C是的中点.求证:∠A=∠B.
19.如图,AB是⊙O直径,弦CD与AB相交于点E,∠ADC=26°.求∠CAB的度数.
20.在证明圆周角定理时,某学习小组讨论出圆心与圆周角有三种不同的位置关系(如图1,2,3所示),小敏说:当圆心O在∠ACB的边上时,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.小亮说:当圆心O在∠ACB的内部或外部时,可以通过添加直径这条辅助线,把问题转化为圆心O在∠ACB的边上时的特殊情形来解决.请选择图2或图3中的一种,完成证明.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半. 已知:如图,在⊙O中,所对的圆周角是∠ACB,圆心角是∠AOB. 求证:∠ACB=∠AOB.
21.如图,AB是⊙O的直径,点C在⊙O上,D是中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整.
解:在⊙O中,
∵D是的中点
∴=,
∴∠1=∠2( )(填推理的依据)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径,
∴∠ADB=90°( )(填推理的依据)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上,
∴∠C+∠B=180°( )(填推理的依据)
∴∠C=180°﹣∠B= (填计算结果)
22.如图,AB为⊙O的直径,弦CD⊥AB于点E,连接BC.若AB=6,∠B=30°,求:弦CD的长.
23.如图,AB=AC,AB是直径,求证:BC=2DE.
24.如图,割线PB与⊙O交于点A,B,割线PC过圆心O,且∠CPB=30°.若PC=13,⊙O的半径OA=5,求弦AB的长.
25.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若BE=8cm,CD=6cm,求⊙O的半径.
参考答案
一.选择题
1.解:∵AB=AC,∠ABC=65°,
∴∠ACB=∠ABC=65°,
∴∠A=180°﹣∠ABC﹣∠ACB=50°,
∴由圆周角定理得:∠BOC=2∠A=100°,
故选:B.
2.解:∵∠C=30°,
∴∠AOB=2∠C=60°,
∵OA=OB,
∴∠ABO=∠BAO=×(180°﹣∠AOB)=60°,
故选:C.
3.解:∵AB是直径,
∴∠ACB=90°,
∵∠ABC=50°,
∴∠A=90°﹣50°=40°,
∴∠BDC的度数为:180°﹣40°=140°
故选:C.
4.解:∵∠C=∠AOB,∠C=40°,
∴∠AOB=80°.
故选:D.
5.解:∵∠ACB=∠AOB=×80°=40°,
∴∠ADB=∠A+∠ACB=60°+40°=100°.
故选:A.
6.解:∵∠ABC=∠AOC,∠ABC+∠AOC=75°,
∴∠AOC+∠AOC=75°,
∴∠AOC=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:D.
7.解:如图:作圆周角∠ADB,使D在优弧上,
∵∠AOB=126°,
∴∠D=∠AOB=63°,
∵∠ACB+∠D=180°,
∴∠ACB=180°﹣63°=117°,
故选:B.
8.解:连接BD,如图,
∵AD为直径,
∴∠ABD=90°,
∵∠ADB=∠ACB=45°,
∴△ABD为等腰直角三角形,
∴AD=AB,
∵AB的长为10cm,
∴AD=10(cm),
故选:B.
二.填空题
9.解:∵AB是△ABC外接圆的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠A=90°﹣35°=55°.
故答案为55°.
10.解:∵∠BOD=2∠A,∠BOD=130°,
∴∠A=65°,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠C=115°,
故答案为:115°.
11.解:连接BC,
∵AB⊥AC,
∴∠BAC=90°,
∴BC是⊙O的直径,
∵AB=6cm,AC=4cm,
∴BC==2(cm),
∴⊙O的半径为:cm.
故答案为:.
12.解:如图,连接AB,
∵∠ACB=90°,
∴AB为圆形镜子的直径,
∵CA=8cm,CB=6cm,
∴AB===10(cm),
∴圆形镜子的半径为×10=5(cm),
故答案为:5.
13.解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AED=20°,
∴∠ACD=20°,
∴∠BCD=∠ACB+∠ACD=110°,
故答案为:110°.
14.解:∵∠BAC与∠BOC所对弧为,
由圆周角定理可知:∠BOC=2∠BAC=60°,
又∵∠AOC=90°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣60°=30°.
故答案为:30°.
15.解:∵AB⊥CD,
∴CE=DE,∠OEC=90°,
∵∠BOC=2∠A=2×22.5°=45°,
∴△OCE为等腰直角三角形,
∴CE=OE=OC=2,
∴CD=2CE=4.
故答案为:4.
16.解:连接OD,
设∠E=x°,
∵AB=2DE,OA=OB=OD,
∴OD=DE,
∴∠E=∠DOE=x°,
∴∠CDO=∠E+∠DOE=2x°,
∵OC=OD,
∴∠C=∠CDO=2x°,
∵∠AOC=57°,∠AOC=∠E+∠C,
∴57=x+2x,
解得:x=19,
即∠E=19°,∠C=38°,
故答案为:38°,19°.
三.解答题
17.解:如图,连接AC.
∵=,∠BAD=50°,
∴∠BAC=∠DAC=∠BAD=×50°=25°,
∵AB为直径,
∴∠ACB=90°,
∴∠∠B=90°﹣∠BAC=90°﹣25°=65°.
18.证明:连接OC.
∵C是的中点,
∴,
∴∠AOC=∠BOC,
在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS),
∴∠A=∠B.
19.解:连接BC,
∵AB是⊙O直径,
∴∠ACB=90°,
∵∠B=∠D=26°,
∴∠CAB=90°﹣26°=64°.
20.证明:如图2:
∵OA=OC,
∴∠A=∠ACO,
∵∠AOD=∠A+∠ACO,
∴∠AOD=2∠ACO,
同理可得:∠BOD=2∠BCO,
∴∠AOB=∠AOD+∠BOD
=2∠ACO+2∠BCO
=2∠ACB,
∴∠ACB=∠AOB;
如图3:∵OA=OC,
∴∠A=∠ACO,
∵∠AOD=∠A+∠ACO,
∴∠AOD=2∠ACO,
同理可得:∠BOD=2∠BCO,
∴∠AOB=∠BOD﹣∠AOD
=2∠BCO﹣2∠ACO
=2∠ACB,
∴∠ACB=∠AOB.
21.解:在⊙O中,
∵D是的中点
∴=,
∴∠1=∠2(等弧所对的圆周角相等)
∵∠BAC=70°
∴∠2=35°
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角)
∴∠B=90°﹣∠2=55°
∵A、B、C、D四个点都在⊙O上,
∴∠C+∠B=180°(圆内接四边形的对角互补)
∴∠C=180°﹣∠B=125°
故答案为:等弧所对的圆周角相等,直径所对的圆周角是直角,圆内接四边形的对角互补,125°.
解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°
又AB=6,∠CBA=30°
∴AC=3,∠CAE=60°
∵弦CD⊥AB,AB为⊙O的直径
∴CE=ED
∵Rt△CEA中,CE=,
∴CD=2CE=3.
23.证明:连接AD、DE
∵AB为⊙O的直径
∴∠ADB=90°
∴AD⊥BC
∵AB=AC
∴∠BAD=∠DAC; BC=2BD=2DC
由圆周角定理可知:BD=DE
∴BC=2DE.
24.解:作OH⊥AB于H,
∴AH=BH,
∵PC=13,⊙O的半径OA=OC=5,
∴PO=PC﹣OC=13﹣5=8,
∵∠CPB=30°,
∴OH=PO=4,
∵AH2=AO2﹣OH2,
∴AH2=52﹣42,
∴AH=3,
∴AB=2AH=6.
25.(1)证明:∵OB=OC,
∴∠BCO=∠B,
∵∠B=∠D,
∴∠BCO=∠D;
(2)解:∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=CD=×6=3cm,
∴∠COE=90°,
设⊙O的半径为rcm,则OE=(8﹣r)cm,
在Rt△OCE中,根据勾股定理得:
r2﹣(8﹣r)2=32,
解得r=,
∴⊙O的半径为cm.
同课章节目录
