平移
图片预览











文档简介
(共113张PPT)
5.4平移
运动1
在车站以及 百货大楼, 人们乘自动电梯上楼或下楼.
运动2
在旅游景点,经常可以看到人们乘缆车沿索道缓缓上山或下山.
运动3
在工厂,产品 整齐地在传送带上沿着生产线从一个生产工位流向另一个生产工位.
大厦里的电梯
运动4
辘轳上的水桶
运动5
分组讨论
以上几种运动现象 有什么共同点?
活动1
创设情境
观察升旗前后的变化
活动1
观察这些天鹅飞行的前后有什么变化
1、传送带上的电视机的形状大小在运送过程中是否发生了变化?
2、在传送带上,如果电视机的某一按键向前移动了80cm,那么电视机的其它部位(如屏幕左上角的图标)向什么方向移动?移动了多少距离?
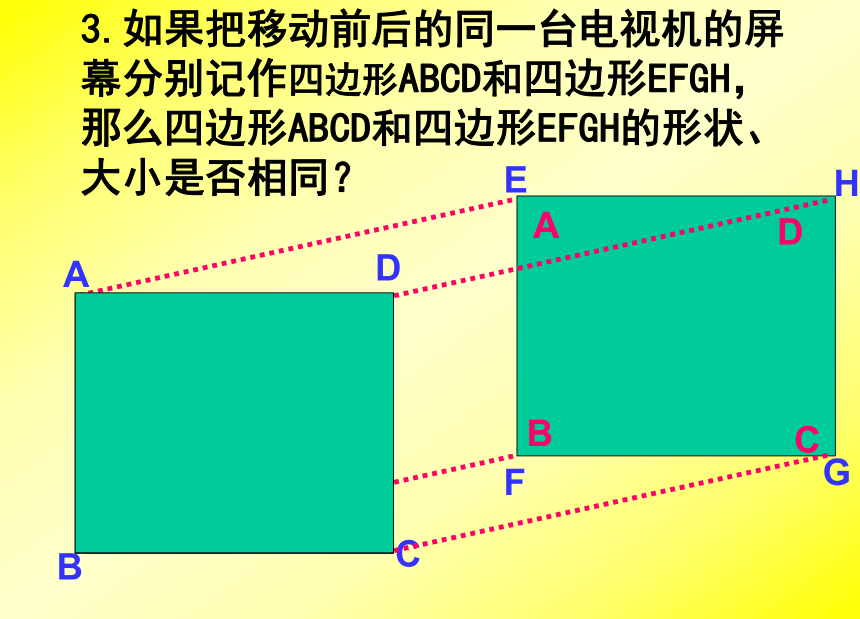
3.如果把移动前后的同一台电视机的屏 幕分别记作四边形ABCD和四边形EFGH,那么四边形ABCD和四边形EFGH的形状、大小是否相同?
A
B
C
D
E
F
G
H
A
D
B
C
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
开启 智慧
定义
平移
你认为属于平移的有哪些?
(1)
(2)
(3)
(4)
(5)
(6)
体验平移
1、你能将左边的图案继续向右画下去吗?请选择其中的一图画一画。
2、学生小组交流,你发现在前后两图的位置、大小和形状有什么变化?
结论:只改变了图形的___,不改变图形的__________。
位置
大小和形状
活动3
这些移动都是平移吗?
探究规律
A
B
C
A'
B'
C'
对应点
连接对应点的线段
几何画板
活动4
(1) 平移后,对应线段_____________
(2) 平移后,对应角______________
(3) 平移后,对应点所连的线段______________
(4) 平移后,新图形和原图形是一对_________
4、经过平移,图形上的每个点都沿着____________移动了________的距离,因此
同一方向
相同
平行且相等
相等
平行且相等
全等图形
A
B
C
A'
B'
C'
X
Y
A
B
C
D
E
F
五、做一做
如图,在方格纸上将△ABC先右平移6格,再向上平移2格,得到平移后的△DEF, 连接平移后的对应点,找出图中几组平行且相等的线段、几组相等的角和一组全等三角形,并说明理由。
AD∥BE∥CF,AD=BE=CF;
AB∥DE,AB=DE;
AC∥DF,AC=DF;
BC∥EF,BC=EF;
∠BAC=∠EDF, ∠ABC=∠DEF, ∠ACB=∠DFE;
△ABC≌△DEF.
1、平移后的图形与原来的图形的对应线段平行且相等,对应角相等;
4、平移的方向移动方向,平移的距离是对应点的长度。
概括
2、在平移过程中,对应线段也可能在一条直线上,如BC与EF;
3、平移后图形的形状与大小都没有变化;
(1)对应线段平行并且相等
(2)三角形上的每一点都作了相同的平移
(3)平移后对应点所连的线段平行且相等
P
Q
M
A
B
C
A
B
C
如图所示,△ABC经过平移到△A′B′C′的位置,指出平移的方向,并量出平移的距离
(1)先找到对应点;
(2)连结两个对应点;
答:所以平移的方向就是点A到点A′的方向
平移的距离就是线段AA′的长度,约为2.6厘米
A
B
C
对应点所连的线段可能在一条直线上。
6、如图,方格纸中的三角形要由位置(1)平移到位置(2),应该先向_____平移_____格,再向______平移_____格
请看图片,图形的平移是由什么决定的?
由移动的方向和距离所决定
将图中的小船向左平移四格,再向下平移一格。
实验
§1 生活中的平移
点的平移:
线的平移:
平面图形的平移:
空间几何体的平移:
§1 生活中的平移
单次平移:
多次平移:
同方向:
不同方向:
§1 生活中的平移
匀速平移:
变速平移:
加速平移:
减速平移:
§1 生活中的平移
沿直线平移(略)
沿曲线平移:
§1 生活中的平移
有形的平移(略)
无形的平移:
听得到的平移
翻译与平移
§1 生活中的平移
有形的平移(略)
无形的平移:
听得到的平移
翻译与平移
Translation n. 平移;翻译
我们是学生。
We are students.
§1 生活中的平移
平移的定义:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动称为平移.
平移的性质:
平移不改变图形的大小、形状与定向;
平移前后两图形对应点所连线段平行且相等,对应线段平行且相等,对应角相等.
平移的判定方法:利用平移的性质进行判定平移的存在.
平移的普遍性:平移广泛存在于我们的生活中.
简单性与复杂性:简单图形平移的复合可以产生复杂且美妙的图案,可见复杂性蕴藏于简单性之中. 研究平移的规律可以帮助我们化繁为简,化难为易.
经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
知识源于悟
3、平移的性质
4
在下面的八幅图案中,②③④⑤⑥⑦⑧中的哪个图案可以通过平移图案①得到?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
下面的五幅画中,(2)(3)(4)(5) 中的哪个图案可以通过平移图案(1)得到
(2)
(3)
(4)
(5)
(1)
1.
分辨一下:
走进知识平台:
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
2.
5
欣赏并说出下列各商标图案哪些是利用平移来设计的?
(1) (2) (3) (4) (5) (6)
6、下图中,图形(2)可以通过图形(1)平移得到吗?
(1)
(2)
(不考虑颜色)
动画演示
上图是由若干个小人形状的图案拼成的.你能用平移分析这个图案是如何形成的吗?
七、数学理解
火车在一段笔直的铁轨上行驶,这个过程可以看成是车厢沿着铁轨的方向平移的过程。如果火车驶入弯道,这时还可以看成是平吗?说说你的理由。
3. 如图,∠DEF是∠ABC经过平移得到的,∠ABC=33 ,则∠DEF=
4. 3米长的卡车朝前一直行驶。若卡车头前进了100米,则卡车尾前进了 米。
33
100
A
B
C
D
E
F
A
B
C
D
E
F
1. 如图,Rt△DEF是由△ABC平移得到的,已知Rt△DEF中, ∠E= 90 ,∠F=35 ,DE=10cm, EF=12cm, 则△ABC中, ∠C= , ∠B= , ∠A= ,
S
△ABC
=
35
90
55
60cm
90
35
10cm
12cm
跨入知识阶梯:
2. 如图,由三角形ABC平移得到的三角形有几个?
A
B
C
给你一幅图案,你能找出基本图形,并再现平移过程吗?
试一试
下列现象中,属于平移的是:
(1)打针时针管的移动
(2)射出的子弹
(3)火车在笔直的铁轨上行驶
(4)冷水受热过程中小气泡上升变成大气泡
(5)人在楼梯上走
(6)钟摆的摆动
(7)飞机起飞前在直线跑道上滑动
(1)(3)(7)
议一议
例1、下列各组图形中,那一组可以通过平移得到( )
跟练:下列图案中的一个三角形不是由另一个三角形平移后得到的是( )
B
C
例2、如图所示,每个小正方形的边长都为1,四边形ABCD平移至四边形A‘B’C‘D’的位置,则∠DCB的对应角是 ,AB的对应线段是 ,点B的对应点是 ,平移的距离 ,平移的方向是 。
跟练:如图所示,△A‘B’C‘是由△ABC通过平移得到的,则线段AC 的对应线段是 ,∠ABC的对应角 ,平移的距离是 ,平移的方向是 (每个小正方形的边长都是1).
4根火柴棒形成如图所示的“口”字,平移火柴棒后原图能变成的汉字是( )
A B C D
B
1、填空:
⑴图形的平移是由 和 决定的.
⑵如图,△ABC经过平移到△A'B'C'的位置,则平移的方向是 ,平移的距离是 。
⑶△ABC经过平移后成为△DEF,那么点A的对应点 ,是点B的对应点是 ,点 的对应点是点F,线段AB的对应线段是 ,线段BC的对应线段是 ,∠A的对应角是 , 的对应角是∠F
⑷如图所示,△ABC是△DEF经过平移得到的,若AD=4cm,则BE= ,CF= ,若P为AB中点,Q为DE中点,则PQ=
2、选择
⑴在下列各项中哪一组右边的图形是左边图形经过平移得到的( )
⑵在5×5方格纸中将图1中的图形N平移后的位置如图2中所示,那么正确的平移方法是( )
A先向下移动1格,再向左移动1格 B先向下移动1格,再向左移动2格
C先向下移动2格,再向左移动1格 D先向下移动2格,再向左移动2格
图1 图2
B
C
3、画图
如图△ABC沿着一定方向平移到△A'B'C',,其中点A移动到点A',且点A'已在图中标明,请画出△A'B'C'。
快乐平移:
如图所示是由4根火柴棍拼成的“小撮子”,撮子内有一粒“米”,请你通过平移2根火柴,让“米”在撮子外。(平移后撮子形状、大小不变)
●
6、生活中的平移
将△ABC在图中平移,(平移时△ABC的三个顶点一定落在图中两线交点上),最多能平移几次?
A
B
C
解:能平移三次,做法如下:
(1)
(2)
(3)
攀登知识高峰:
如图所示,在Rt △ ABC中,∠C= 90 ,BC=AC=4,将△ ABC沿CB方向平移到△ A'B'C'的位置。若平移的距离为3,求△ ABC与△ A'B'C'重叠部分的面积.
A
B
C
A'
C'
B'
D
通过本节课的学习,你有哪些收获 还有什么疑问
教材分析
《生活中的平移》在初中数学图形变换中承接七年级下册轴对称,并且为学习图形的旋转打下基础
地位作用
能力目标
情感目标
知识目标
教学目标
掌握平移的定义和性质
经历观察,分析,操作欣赏平移情况,探索归纳图形平移的定义,性质。发展学生空间感觉。积累数学学习经验,提高合作交流能力。
通过探索,创造,感受成功的喜悦,提高学习兴趣增强信心,学会欣赏。
教材分析
总结平移定义,探索平移性质,利用平移性质解决问题。
重 点
难 点
学生自主探究,合作交流获得平移性质。
教、学法分析
教法:
教师利用多媒体手段,情境吸引,实例展示。在数学实验中适当点拨与激励。设计梯度练习,展示精美图片,带领学生在平移变换的世界中探索规律,揭示奥秘。
学生观察思考,动手操作,自主探究,合作交流,阶梯训练,利用这些方法掌握课堂重点。
学法:
一、情境引入,初步感知
二、研究问题,得出定义
三、数学实验,探索规律
四、阶梯练习,运用新知
五、学生归纳,感悟点滴
复 习 回 顾
1.什么是平移
3.平移的基本性质是什么
在平面内,将一个图形沿某个方向移动
一定的距离,这样的图形运动称为平移。
2.平移的特点是什么?
平移不改变图形的形状和大小。
经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
简单的平移作图
如图所示:经过平移,线段AB的端点A移到了点D,你能作出线段AB平移后的图形吗 请大家讨论一下。
A
B
.
D
A
B
.
D
C
平移的基本性质
请同学们思考一下:
平移作图的依据是什么?
例题1:经过平移, ABC顶点
A移到了点D作出平移后的三角形。
A
B
C
D
E
F
A
B
C
D
学 生 交 流
还有其它方法吗
确定图形平移后的位置,
除需要原来的位置,还
需要什么条件?
A
B
C
D
F
E
.D
A
B
C
.D
A
B
1. 原图形
2. 平移的方向
3. 平移的距离
确定图形平移后位置的三要素:
例2. 如图.将字母A按箭头所指的方向
平移 3cm,作出平移后的图形.
3cm
A1
B1
C1
A
C
B
D
E
E1
D1
随 堂 练 习
1. 将图中的字母N沿水平
方向向右平移3cm,作出
平移后的图形.
A
B
C
D
B1
C1
A1
D1
B
D
C
2. 线段CD是线段AB平移后
的图形,D是B的对应点,
作出线段AB。
B
D
C
A
课 堂 小 结
通过本节学习,会作出简单平面图形平移后的图形
知道平移作图的依据是平移的基本性质及确定图形平移后位置的三要素
吴 菲
周 南 中 学
平移的定义:
在平面内,将一个图形沿某个方向移动一定的距离,这样
的图形运动称为平移。平移不改变图形的形状和大小。
平移的性质:
经过平移,对应点所连的线段平行且相等;对应线段平行
且相等,对应角相等。
引例:
线段AB的端点A移到了点D,试作出线段AB平移后
的图形。
A
B
?
D
E
想一想,还有别的作法吗
方法:
根据平移的定义和
性质可以作出平移
后的图形。
注意:平移线段一般
找端点.
A
B
B’
A’
方法二:
利用平移不改变图
的形状和大小的性
质作图。
(过一定点作已知
直线的平行线)
例一:
经过平移,三角形ABC的顶点A移到了点D(如图所示),
试作出平移后的三角形。
A
B
C
D
F
E
作图步骤:
1、找关键点A、B、C。
2、找定方向定距离:连接 AD。
3、利用平移的性质找到B、C的对应点E、F。
4、分别连接DE、DF、EF。
方法二:
B
C
A
D
E
F
动动脑:
确定一个图形平移后的位置,需要什么条件?
图形原来的位置、平移的方向、平移的距离
更多方法
过定点D分别作AB、AC的平行线,截等长找关键点
的对应点。
A
B
C
A’
B’
C’
D
E
D’
E’
怎样把字母A按箭头方向平移3cm
3cm
3cm
A
B
C
D
F
A’
C’
方法二:
利用对应线段形状大小不变
D’
更多方法
随堂练习
将图中的字母N沿水平方向向右平移3cm,作出
平移后的图形。
3cm
更多方法
试一试:
图中的窗棂轮廓是由一个半圆和一个矩形组成,试
作出这个图案向左平移6格后的图案。
观察下面图案:
(1)这个图案有什么特点?
(2)它可以通过什么“基本图案”经过怎样的平移而形成?
(3)在平移的过程中,“基本图案”的大小、形状、位置是否
发生了变化?你能解释其中的道理吗?
平移作图的三要素:
1、找关键点。
2、找定距离、定方向。
3、找出关键点的对应点。
4、连接对应线段。
原图形、定方向、定距离。
平移作图的步骤:
3cm
A
B
A’
B’
C
D
C’
D’
方法二:
平移前后不改变线段长度和对应角大小
返回
B
C
方法三:
利用平移的定义
和性质作图.
(对应角相等)
1、找到关键点
A,B,C。
A
D
2、过点D作与AB平行的直线。
E
作图步骤:
3、作∠EDF等于∠ BAC,并截取DE=AB,找到点E。
4、同理找到点F,连接EF,则△DEF即为△ ABC
平移后的图形。
F
返回
3cm
方法三:
利用平移前后对应角相等作图
返回
返回
返回
返回
能经过平移吗
能经过轴对称吗?
还有其他的方式吗
5.4平移
运动1
在车站以及 百货大楼, 人们乘自动电梯上楼或下楼.
运动2
在旅游景点,经常可以看到人们乘缆车沿索道缓缓上山或下山.
运动3
在工厂,产品 整齐地在传送带上沿着生产线从一个生产工位流向另一个生产工位.
大厦里的电梯
运动4
辘轳上的水桶
运动5
分组讨论
以上几种运动现象 有什么共同点?
活动1
创设情境
观察升旗前后的变化
活动1
观察这些天鹅飞行的前后有什么变化
1、传送带上的电视机的形状大小在运送过程中是否发生了变化?
2、在传送带上,如果电视机的某一按键向前移动了80cm,那么电视机的其它部位(如屏幕左上角的图标)向什么方向移动?移动了多少距离?
3.如果把移动前后的同一台电视机的屏 幕分别记作四边形ABCD和四边形EFGH,那么四边形ABCD和四边形EFGH的形状、大小是否相同?
A
B
C
D
E
F
G
H
A
D
B
C
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
开启 智慧
定义
平移
你认为属于平移的有哪些?
(1)
(2)
(3)
(4)
(5)
(6)
体验平移
1、你能将左边的图案继续向右画下去吗?请选择其中的一图画一画。
2、学生小组交流,你发现在前后两图的位置、大小和形状有什么变化?
结论:只改变了图形的___,不改变图形的__________。
位置
大小和形状
活动3
这些移动都是平移吗?
探究规律
A
B
C
A'
B'
C'
对应点
连接对应点的线段
几何画板
活动4
(1) 平移后,对应线段_____________
(2) 平移后,对应角______________
(3) 平移后,对应点所连的线段______________
(4) 平移后,新图形和原图形是一对_________
4、经过平移,图形上的每个点都沿着____________移动了________的距离,因此
同一方向
相同
平行且相等
相等
平行且相等
全等图形
A
B
C
A'
B'
C'
X
Y
A
B
C
D
E
F
五、做一做
如图,在方格纸上将△ABC先右平移6格,再向上平移2格,得到平移后的△DEF, 连接平移后的对应点,找出图中几组平行且相等的线段、几组相等的角和一组全等三角形,并说明理由。
AD∥BE∥CF,AD=BE=CF;
AB∥DE,AB=DE;
AC∥DF,AC=DF;
BC∥EF,BC=EF;
∠BAC=∠EDF, ∠ABC=∠DEF, ∠ACB=∠DFE;
△ABC≌△DEF.
1、平移后的图形与原来的图形的对应线段平行且相等,对应角相等;
4、平移的方向移动方向,平移的距离是对应点的长度。
概括
2、在平移过程中,对应线段也可能在一条直线上,如BC与EF;
3、平移后图形的形状与大小都没有变化;
(1)对应线段平行并且相等
(2)三角形上的每一点都作了相同的平移
(3)平移后对应点所连的线段平行且相等
P
Q
M
A
B
C
A
B
C
如图所示,△ABC经过平移到△A′B′C′的位置,指出平移的方向,并量出平移的距离
(1)先找到对应点;
(2)连结两个对应点;
答:所以平移的方向就是点A到点A′的方向
平移的距离就是线段AA′的长度,约为2.6厘米
A
B
C
对应点所连的线段可能在一条直线上。
6、如图,方格纸中的三角形要由位置(1)平移到位置(2),应该先向_____平移_____格,再向______平移_____格
请看图片,图形的平移是由什么决定的?
由移动的方向和距离所决定
将图中的小船向左平移四格,再向下平移一格。
实验
§1 生活中的平移
点的平移:
线的平移:
平面图形的平移:
空间几何体的平移:
§1 生活中的平移
单次平移:
多次平移:
同方向:
不同方向:
§1 生活中的平移
匀速平移:
变速平移:
加速平移:
减速平移:
§1 生活中的平移
沿直线平移(略)
沿曲线平移:
§1 生活中的平移
有形的平移(略)
无形的平移:
听得到的平移
翻译与平移
§1 生活中的平移
有形的平移(略)
无形的平移:
听得到的平移
翻译与平移
Translation n. 平移;翻译
我们是学生。
We are students.
§1 生活中的平移
平移的定义:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动称为平移.
平移的性质:
平移不改变图形的大小、形状与定向;
平移前后两图形对应点所连线段平行且相等,对应线段平行且相等,对应角相等.
平移的判定方法:利用平移的性质进行判定平移的存在.
平移的普遍性:平移广泛存在于我们的生活中.
简单性与复杂性:简单图形平移的复合可以产生复杂且美妙的图案,可见复杂性蕴藏于简单性之中. 研究平移的规律可以帮助我们化繁为简,化难为易.
经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
知识源于悟
3、平移的性质
4
在下面的八幅图案中,②③④⑤⑥⑦⑧中的哪个图案可以通过平移图案①得到?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
下面的五幅画中,(2)(3)(4)(5) 中的哪个图案可以通过平移图案(1)得到
(2)
(3)
(4)
(5)
(1)
1.
分辨一下:
走进知识平台:
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
2.
5
欣赏并说出下列各商标图案哪些是利用平移来设计的?
(1) (2) (3) (4) (5) (6)
6、下图中,图形(2)可以通过图形(1)平移得到吗?
(1)
(2)
(不考虑颜色)
动画演示
上图是由若干个小人形状的图案拼成的.你能用平移分析这个图案是如何形成的吗?
七、数学理解
火车在一段笔直的铁轨上行驶,这个过程可以看成是车厢沿着铁轨的方向平移的过程。如果火车驶入弯道,这时还可以看成是平吗?说说你的理由。
3. 如图,∠DEF是∠ABC经过平移得到的,∠ABC=33 ,则∠DEF=
4. 3米长的卡车朝前一直行驶。若卡车头前进了100米,则卡车尾前进了 米。
33
100
A
B
C
D
E
F
A
B
C
D
E
F
1. 如图,Rt△DEF是由△ABC平移得到的,已知Rt△DEF中, ∠E= 90 ,∠F=35 ,DE=10cm, EF=12cm, 则△ABC中, ∠C= , ∠B= , ∠A= ,
S
△ABC
=
35
90
55
60cm
90
35
10cm
12cm
跨入知识阶梯:
2. 如图,由三角形ABC平移得到的三角形有几个?
A
B
C
给你一幅图案,你能找出基本图形,并再现平移过程吗?
试一试
下列现象中,属于平移的是:
(1)打针时针管的移动
(2)射出的子弹
(3)火车在笔直的铁轨上行驶
(4)冷水受热过程中小气泡上升变成大气泡
(5)人在楼梯上走
(6)钟摆的摆动
(7)飞机起飞前在直线跑道上滑动
(1)(3)(7)
议一议
例1、下列各组图形中,那一组可以通过平移得到( )
跟练:下列图案中的一个三角形不是由另一个三角形平移后得到的是( )
B
C
例2、如图所示,每个小正方形的边长都为1,四边形ABCD平移至四边形A‘B’C‘D’的位置,则∠DCB的对应角是 ,AB的对应线段是 ,点B的对应点是 ,平移的距离 ,平移的方向是 。
跟练:如图所示,△A‘B’C‘是由△ABC通过平移得到的,则线段AC 的对应线段是 ,∠ABC的对应角 ,平移的距离是 ,平移的方向是 (每个小正方形的边长都是1).
4根火柴棒形成如图所示的“口”字,平移火柴棒后原图能变成的汉字是( )
A B C D
B
1、填空:
⑴图形的平移是由 和 决定的.
⑵如图,△ABC经过平移到△A'B'C'的位置,则平移的方向是 ,平移的距离是 。
⑶△ABC经过平移后成为△DEF,那么点A的对应点 ,是点B的对应点是 ,点 的对应点是点F,线段AB的对应线段是 ,线段BC的对应线段是 ,∠A的对应角是 , 的对应角是∠F
⑷如图所示,△ABC是△DEF经过平移得到的,若AD=4cm,则BE= ,CF= ,若P为AB中点,Q为DE中点,则PQ=
2、选择
⑴在下列各项中哪一组右边的图形是左边图形经过平移得到的( )
⑵在5×5方格纸中将图1中的图形N平移后的位置如图2中所示,那么正确的平移方法是( )
A先向下移动1格,再向左移动1格 B先向下移动1格,再向左移动2格
C先向下移动2格,再向左移动1格 D先向下移动2格,再向左移动2格
图1 图2
B
C
3、画图
如图△ABC沿着一定方向平移到△A'B'C',,其中点A移动到点A',且点A'已在图中标明,请画出△A'B'C'。
快乐平移:
如图所示是由4根火柴棍拼成的“小撮子”,撮子内有一粒“米”,请你通过平移2根火柴,让“米”在撮子外。(平移后撮子形状、大小不变)
●
6、生活中的平移
将△ABC在图中平移,(平移时△ABC的三个顶点一定落在图中两线交点上),最多能平移几次?
A
B
C
解:能平移三次,做法如下:
(1)
(2)
(3)
攀登知识高峰:
如图所示,在Rt △ ABC中,∠C= 90 ,BC=AC=4,将△ ABC沿CB方向平移到△ A'B'C'的位置。若平移的距离为3,求△ ABC与△ A'B'C'重叠部分的面积.
A
B
C
A'
C'
B'
D
通过本节课的学习,你有哪些收获 还有什么疑问
教材分析
《生活中的平移》在初中数学图形变换中承接七年级下册轴对称,并且为学习图形的旋转打下基础
地位作用
能力目标
情感目标
知识目标
教学目标
掌握平移的定义和性质
经历观察,分析,操作欣赏平移情况,探索归纳图形平移的定义,性质。发展学生空间感觉。积累数学学习经验,提高合作交流能力。
通过探索,创造,感受成功的喜悦,提高学习兴趣增强信心,学会欣赏。
教材分析
总结平移定义,探索平移性质,利用平移性质解决问题。
重 点
难 点
学生自主探究,合作交流获得平移性质。
教、学法分析
教法:
教师利用多媒体手段,情境吸引,实例展示。在数学实验中适当点拨与激励。设计梯度练习,展示精美图片,带领学生在平移变换的世界中探索规律,揭示奥秘。
学生观察思考,动手操作,自主探究,合作交流,阶梯训练,利用这些方法掌握课堂重点。
学法:
一、情境引入,初步感知
二、研究问题,得出定义
三、数学实验,探索规律
四、阶梯练习,运用新知
五、学生归纳,感悟点滴
复 习 回 顾
1.什么是平移
3.平移的基本性质是什么
在平面内,将一个图形沿某个方向移动
一定的距离,这样的图形运动称为平移。
2.平移的特点是什么?
平移不改变图形的形状和大小。
经过平移,对应点所连的线段平行且相等;对应线段平行且相等,对应角相等。
简单的平移作图
如图所示:经过平移,线段AB的端点A移到了点D,你能作出线段AB平移后的图形吗 请大家讨论一下。
A
B
.
D
A
B
.
D
C
平移的基本性质
请同学们思考一下:
平移作图的依据是什么?
例题1:经过平移, ABC顶点
A移到了点D作出平移后的三角形。
A
B
C
D
E
F
A
B
C
D
学 生 交 流
还有其它方法吗
确定图形平移后的位置,
除需要原来的位置,还
需要什么条件?
A
B
C
D
F
E
.D
A
B
C
.D
A
B
1. 原图形
2. 平移的方向
3. 平移的距离
确定图形平移后位置的三要素:
例2. 如图.将字母A按箭头所指的方向
平移 3cm,作出平移后的图形.
3cm
A1
B1
C1
A
C
B
D
E
E1
D1
随 堂 练 习
1. 将图中的字母N沿水平
方向向右平移3cm,作出
平移后的图形.
A
B
C
D
B1
C1
A1
D1
B
D
C
2. 线段CD是线段AB平移后
的图形,D是B的对应点,
作出线段AB。
B
D
C
A
课 堂 小 结
通过本节学习,会作出简单平面图形平移后的图形
知道平移作图的依据是平移的基本性质及确定图形平移后位置的三要素
吴 菲
周 南 中 学
平移的定义:
在平面内,将一个图形沿某个方向移动一定的距离,这样
的图形运动称为平移。平移不改变图形的形状和大小。
平移的性质:
经过平移,对应点所连的线段平行且相等;对应线段平行
且相等,对应角相等。
引例:
线段AB的端点A移到了点D,试作出线段AB平移后
的图形。
A
B
?
D
E
想一想,还有别的作法吗
方法:
根据平移的定义和
性质可以作出平移
后的图形。
注意:平移线段一般
找端点.
A
B
B’
A’
方法二:
利用平移不改变图
的形状和大小的性
质作图。
(过一定点作已知
直线的平行线)
例一:
经过平移,三角形ABC的顶点A移到了点D(如图所示),
试作出平移后的三角形。
A
B
C
D
F
E
作图步骤:
1、找关键点A、B、C。
2、找定方向定距离:连接 AD。
3、利用平移的性质找到B、C的对应点E、F。
4、分别连接DE、DF、EF。
方法二:
B
C
A
D
E
F
动动脑:
确定一个图形平移后的位置,需要什么条件?
图形原来的位置、平移的方向、平移的距离
更多方法
过定点D分别作AB、AC的平行线,截等长找关键点
的对应点。
A
B
C
A’
B’
C’
D
E
D’
E’
怎样把字母A按箭头方向平移3cm
3cm
3cm
A
B
C
D
F
A’
C’
方法二:
利用对应线段形状大小不变
D’
更多方法
随堂练习
将图中的字母N沿水平方向向右平移3cm,作出
平移后的图形。
3cm
更多方法
试一试:
图中的窗棂轮廓是由一个半圆和一个矩形组成,试
作出这个图案向左平移6格后的图案。
观察下面图案:
(1)这个图案有什么特点?
(2)它可以通过什么“基本图案”经过怎样的平移而形成?
(3)在平移的过程中,“基本图案”的大小、形状、位置是否
发生了变化?你能解释其中的道理吗?
平移作图的三要素:
1、找关键点。
2、找定距离、定方向。
3、找出关键点的对应点。
4、连接对应线段。
原图形、定方向、定距离。
平移作图的步骤:
3cm
A
B
A’
B’
C
D
C’
D’
方法二:
平移前后不改变线段长度和对应角大小
返回
B
C
方法三:
利用平移的定义
和性质作图.
(对应角相等)
1、找到关键点
A,B,C。
A
D
2、过点D作与AB平行的直线。
E
作图步骤:
3、作∠EDF等于∠ BAC,并截取DE=AB,找到点E。
4、同理找到点F,连接EF,则△DEF即为△ ABC
平移后的图形。
F
返回
3cm
方法三:
利用平移前后对应角相等作图
返回
返回
返回
返回
能经过平移吗
能经过轴对称吗?
还有其他的方式吗
