2023--2024学年人教版八年级数学上册 14.2.1 平方差公式 教学课件 28张PPT
文档属性
| 名称 | 2023--2024学年人教版八年级数学上册 14.2.1 平方差公式 教学课件 28张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
14.2 乘法公式
14.2.1 平方差公式
人教版数学八年级上册
观看视频思考以下问题:
视频中讲述了最强大脑的哪些卓越的能力
回顾显记忆之强
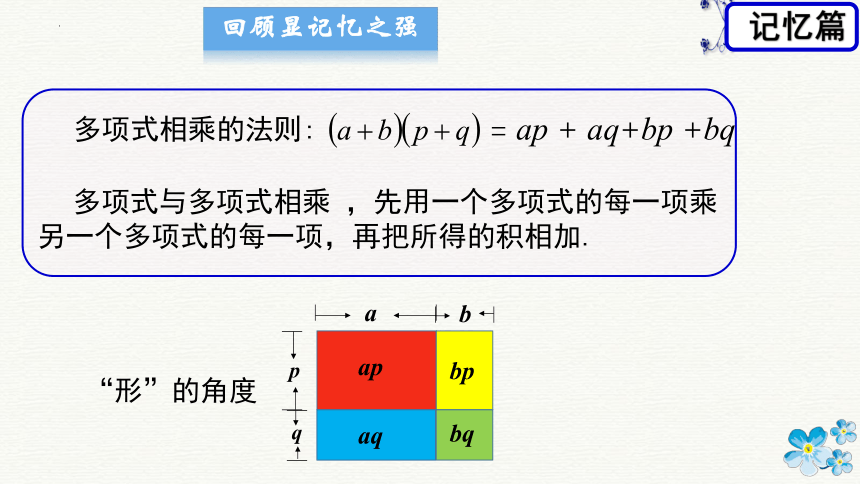
多项式与多项式相乘 ,先用一个多项式的每一项乘
另一个多项式的每一项,再把所得的积相加.
“形”的角度
多项式相乘的法则:
= ap + aq+bp +bq
b
a
p
q
ap
bq
bp
aq
记忆篇
思考:五个算式从结果上看,项数有什么不同?
回顾显记忆之强
计算下列多项式的积
记忆篇
活动要求:
1.独立完成学案探究一.
2.从符号是否正确,结果是否化简等方面自我检查.
3.公布答案后,对照答案,红笔批改并纠错.
观察寻规律之本
思考:
1.三个式子的左边具有什么特征?计算结果有什么共同特征?
猜想:
观察篇
2.能否用含字母a,b的式子表示具有以上特征的多项式乘法?
推理显逻辑之密
代数证明
(a+b)(a-b)=a2-b2
(a+b)(a-b)
= a -ab+ab-b
= a2-b2
解:
多项式的乘法法则
(a+b)(p+q)
=ap+aq+bp+bq
两个数的和与这两个数的差的积,等于这两个数的平方差.
公式显智慧结晶
平方差公式
和
差
平方差
积
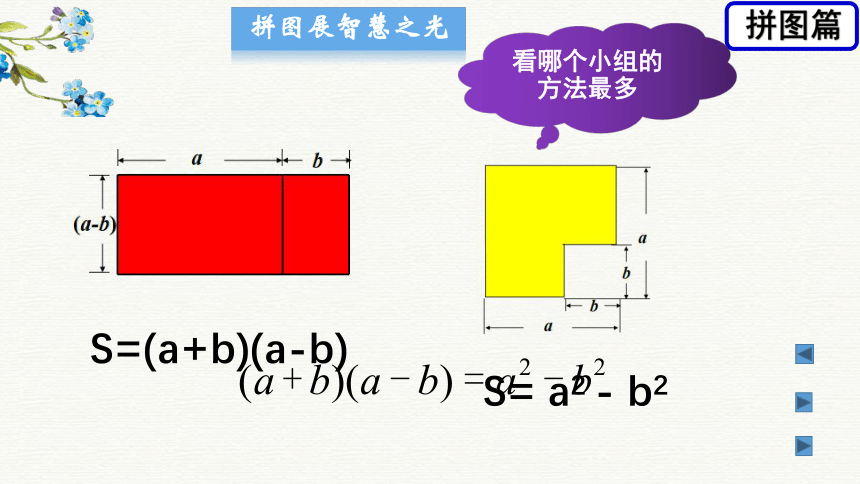
拼图展智慧之光
拼图篇
看哪个小组的方法最多
S=(a+b)(a-b)
S= a2 - b2
例1 运用平方差公式计算
分析:在(1)中,可以把3x看成a, 2看成b, 即
解:
携手探经典之例
( )
9
温馨提示:
1.整体加括号.
2.系数要平方.
步骤:①确定a, b
②运用公式
③计算结果
携手探经典之例
特征明公式之巧
完全相同
只有前面符号不同
如何准确的确定公式中的a, b呢?
观察篇
下列各式能否运用平方差公式计算?并说明理由
快速抢答
否
否
能
能
能
公式中的字母a, b可以表示具体的数(正数或负数),也可以表示单项式或多项式等式子.
在信封中找出两个多项式使它们的积能够符合平方差公式的形式,看哪个小组找的既快又准确.
活动
例2 计算
解:
速算显数学之用
( )
速算篇
活动要求:
1.小组内交流解题思路.
2.小组代表展示交流成果.
导图理知识之网
1.本节课学习
的数学知识
是什么?
2.我们是如何
得到它的?
3.它的用途
是什么?
4.它与多项式乘法
的联系是什么?
平方差公式
数形结合
特殊到一般
计算猜想
推理验证
拼图验证
简化计算
面积问题
速算
完全平方公式
类比
反思享收获之乐
多项式相乘的法则:
一般到特殊
教师寄语
愿每位同学都能拥有“最强大脑”,张开“观察”的双眼,展开“拼图”、“速算”的双翅,乘着“记忆”的东风,扶摇直上,在数学的天空中自由翱翔,飞出真我的风采。
必做题:课本108页练习1、2;
拓展题:计算 ;
研究性作业:类比平方差公式的探究方法,来探究
完全平方公式.
作业
谢谢大家
b
a
(a-b)
a
a
b
b
b
a
(a-b)
b
a
(a-b)
a
b
a
(a-b)
a
b
b
a
b
a
(a-b)
a
b
b
a
a
b
b
b
a
(a-b)
a
a
b
b
b
a
(a-b)
b
a
(a-b)
14.2 乘法公式
14.2.1 平方差公式
人教版数学八年级上册
观看视频思考以下问题:
视频中讲述了最强大脑的哪些卓越的能力
回顾显记忆之强
多项式与多项式相乘 ,先用一个多项式的每一项乘
另一个多项式的每一项,再把所得的积相加.
“形”的角度
多项式相乘的法则:
= ap + aq+bp +bq
b
a
p
q
ap
bq
bp
aq
记忆篇
思考:五个算式从结果上看,项数有什么不同?
回顾显记忆之强
计算下列多项式的积
记忆篇
活动要求:
1.独立完成学案探究一.
2.从符号是否正确,结果是否化简等方面自我检查.
3.公布答案后,对照答案,红笔批改并纠错.
观察寻规律之本
思考:
1.三个式子的左边具有什么特征?计算结果有什么共同特征?
猜想:
观察篇
2.能否用含字母a,b的式子表示具有以上特征的多项式乘法?
推理显逻辑之密
代数证明
(a+b)(a-b)=a2-b2
(a+b)(a-b)
= a -ab+ab-b
= a2-b2
解:
多项式的乘法法则
(a+b)(p+q)
=ap+aq+bp+bq
两个数的和与这两个数的差的积,等于这两个数的平方差.
公式显智慧结晶
平方差公式
和
差
平方差
积
拼图展智慧之光
拼图篇
看哪个小组的方法最多
S=(a+b)(a-b)
S= a2 - b2
例1 运用平方差公式计算
分析:在(1)中,可以把3x看成a, 2看成b, 即
解:
携手探经典之例
( )
9
温馨提示:
1.整体加括号.
2.系数要平方.
步骤:①确定a, b
②运用公式
③计算结果
携手探经典之例
特征明公式之巧
完全相同
只有前面符号不同
如何准确的确定公式中的a, b呢?
观察篇
下列各式能否运用平方差公式计算?并说明理由
快速抢答
否
否
能
能
能
公式中的字母a, b可以表示具体的数(正数或负数),也可以表示单项式或多项式等式子.
在信封中找出两个多项式使它们的积能够符合平方差公式的形式,看哪个小组找的既快又准确.
活动
例2 计算
解:
速算显数学之用
( )
速算篇
活动要求:
1.小组内交流解题思路.
2.小组代表展示交流成果.
导图理知识之网
1.本节课学习
的数学知识
是什么?
2.我们是如何
得到它的?
3.它的用途
是什么?
4.它与多项式乘法
的联系是什么?
平方差公式
数形结合
特殊到一般
计算猜想
推理验证
拼图验证
简化计算
面积问题
速算
完全平方公式
类比
反思享收获之乐
多项式相乘的法则:
一般到特殊
教师寄语
愿每位同学都能拥有“最强大脑”,张开“观察”的双眼,展开“拼图”、“速算”的双翅,乘着“记忆”的东风,扶摇直上,在数学的天空中自由翱翔,飞出真我的风采。
必做题:课本108页练习1、2;
拓展题:计算 ;
研究性作业:类比平方差公式的探究方法,来探究
完全平方公式.
作业
谢谢大家
b
a
(a-b)
a
a
b
b
b
a
(a-b)
b
a
(a-b)
a
b
a
(a-b)
a
b
b
a
b
a
(a-b)
a
b
b
a
a
b
b
b
a
(a-b)
a
a
b
b
b
a
(a-b)
b
a
(a-b)
