24.1.3弧、弦、圆心角同步练习2023-2024学年人教版数学九年级上册(含答案)
文档属性
| 名称 | 24.1.3弧、弦、圆心角同步练习2023-2024学年人教版数学九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 345.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
24.1.3弧、弦、圆心角
一、单选题
1.下列命题:①三点确定一个圆;②直径是圆的对称轴;③平分弦的直径垂直于弦;④三角形的外心到三角形三边的距离相等;⑤相等的圆心角所对的弧相等,正确命题的个数是( )
A.0个 B.1个 C.2个 D.3个
2.下列说法中,错误的是( )
A.顶点在圆心的角叫做圆心角
B.等于
C.各边相等的多边形叫做正多边形
D.在数轴上,与表示的点的距离为3的数有2和.
3.如图,为圆O的直径,B为劣弧中点,,则的长为( )
A. B. C.8 D.16
4.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )
A.52° B.60° C.72° D.76°
5.如图,点A,B,C,D均在以点O为圆心的圆O上,连接,及顺次连接O,B,C,D得到四边形,若,,则的度数为( )
A. B. C. D.
6.如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是( )
A.60° B.51° C.48° D.76°
7.如图,是的直径,,点B为弧的中点,点P是直径上的一个动点,则的最小值为( )
A.2 B. C. D.3
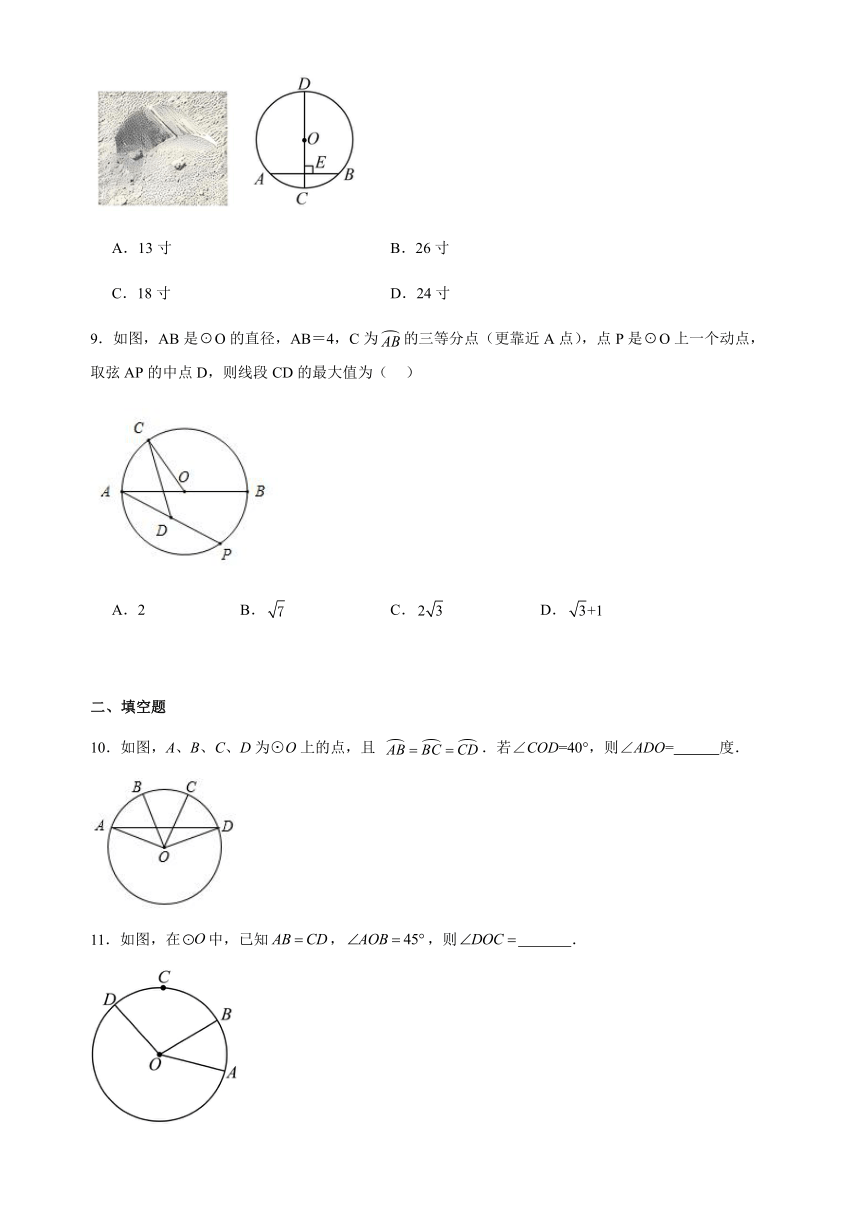
8.《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响. 在《九章算术》中有很多名题,下面就是其中的一道. 原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,为的直径,弦于点. 寸,寸,则可得直径的长为( )
A.13寸 B.26寸
C.18寸 D.24寸
9.如图,AB是O的直径,AB=4,C为的三等分点(更靠近A点),点P是O上一个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
二、填空题
10.如图,A、B、C、D为⊙O上的点,且 .若∠COD=40°,则∠ADO= 度.
11.如图,在中,已知,,则 .
12.如图,AB,CD是⊙O的两条弦,要使AB=CD,需要补充的条件是 (补充一个即可).
13.如图所示,是半径为3的上的两点.若是的中点,则四边形的周长为 .
14.点A、C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .
15.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有 个.
① ;②;③AC=BD;④∠BOD=∠AOC.
三、解答题
16.已知:如图所示,A,B,C,D是⊙上的点,且,,求的度数.
17.如图,在⊙O中,AD=BC,求证:DC=AB.
18.如图,圆心角.
(1)判断和的数量关系,并说明理由;
(2)若,求的度数.
19.如图,四边形内接于,是的直径,点C为的中点,弦于点F,与交于点G.
(1)求证:;
(2)若,求的长.
参考答案:
1.A
2.C
3.A
4.A
5.C
6.B
7.C
8.B
9.D
10.30
11.
12..
13.12
14.或2.
15.4
16..
18.(1)(2)
19.2
一、单选题
1.下列命题:①三点确定一个圆;②直径是圆的对称轴;③平分弦的直径垂直于弦;④三角形的外心到三角形三边的距离相等;⑤相等的圆心角所对的弧相等,正确命题的个数是( )
A.0个 B.1个 C.2个 D.3个
2.下列说法中,错误的是( )
A.顶点在圆心的角叫做圆心角
B.等于
C.各边相等的多边形叫做正多边形
D.在数轴上,与表示的点的距离为3的数有2和.
3.如图,为圆O的直径,B为劣弧中点,,则的长为( )
A. B. C.8 D.16
4.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )
A.52° B.60° C.72° D.76°
5.如图,点A,B,C,D均在以点O为圆心的圆O上,连接,及顺次连接O,B,C,D得到四边形,若,,则的度数为( )
A. B. C. D.
6.如图所示,小范从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小范第五次走到场地边缘时处于弧AB上,此时∠AOE=48°,则α的度数是( )
A.60° B.51° C.48° D.76°
7.如图,是的直径,,点B为弧的中点,点P是直径上的一个动点,则的最小值为( )
A.2 B. C. D.3
8.《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响. 在《九章算术》中有很多名题,下面就是其中的一道. 原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,为的直径,弦于点. 寸,寸,则可得直径的长为( )
A.13寸 B.26寸
C.18寸 D.24寸
9.如图,AB是O的直径,AB=4,C为的三等分点(更靠近A点),点P是O上一个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
二、填空题
10.如图,A、B、C、D为⊙O上的点,且 .若∠COD=40°,则∠ADO= 度.
11.如图,在中,已知,,则 .
12.如图,AB,CD是⊙O的两条弦,要使AB=CD,需要补充的条件是 (补充一个即可).
13.如图所示,是半径为3的上的两点.若是的中点,则四边形的周长为 .
14.点A、C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 .
15.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有 个.
① ;②;③AC=BD;④∠BOD=∠AOC.
三、解答题
16.已知:如图所示,A,B,C,D是⊙上的点,且,,求的度数.
17.如图,在⊙O中,AD=BC,求证:DC=AB.
18.如图,圆心角.
(1)判断和的数量关系,并说明理由;
(2)若,求的度数.
19.如图,四边形内接于,是的直径,点C为的中点,弦于点F,与交于点G.
(1)求证:;
(2)若,求的长.
参考答案:
1.A
2.C
3.A
4.A
5.C
6.B
7.C
8.B
9.D
10.30
11.
12..
13.12
14.或2.
15.4
16..
18.(1)(2)
19.2
同课章节目录
