24.2 点和圆、直线和圆的位置关系同步练习2023-2024学年人教版九年级数学上册(无答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系同步练习2023-2024学年人教版九年级数学上册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览

文档简介
人教版九年级上24.2 点和圆、直线和圆的位置关系
一、选择题
1. 用反证法证明命题“在中,若,,则”时,首先应假设( )
A. B. C. D.
2. 下列命题中真命题的是( )
A.长度相等的弧是等弧 B.相等的圆心角所对的弦相等
C.任意三点确定一个圆 D.圆是中心对称图形,圆心是它的对称中心
3. 已知的半径为5,直线与有2个公共点,则点到直线的距离可能是( )
A.3 B.5 C.7 D.9
4. 如图,是两个同心圆中大圆的弦,且与小圆相切于点C,若两圆半径分别为和,则弦长为( )
A. B. C. D.
5. 已知圆半径为,,,为射线上的三个点,,,,则( )
A.点在内 B.点在上 C.点在外 D.点在上
6. 下列说法正确的是( )
A.等弧所对的圆心角相等 B.相等的弦所对的弧相等
C.过三点一定可以确定一个圆 D.垂直于半径的直线是圆的切线
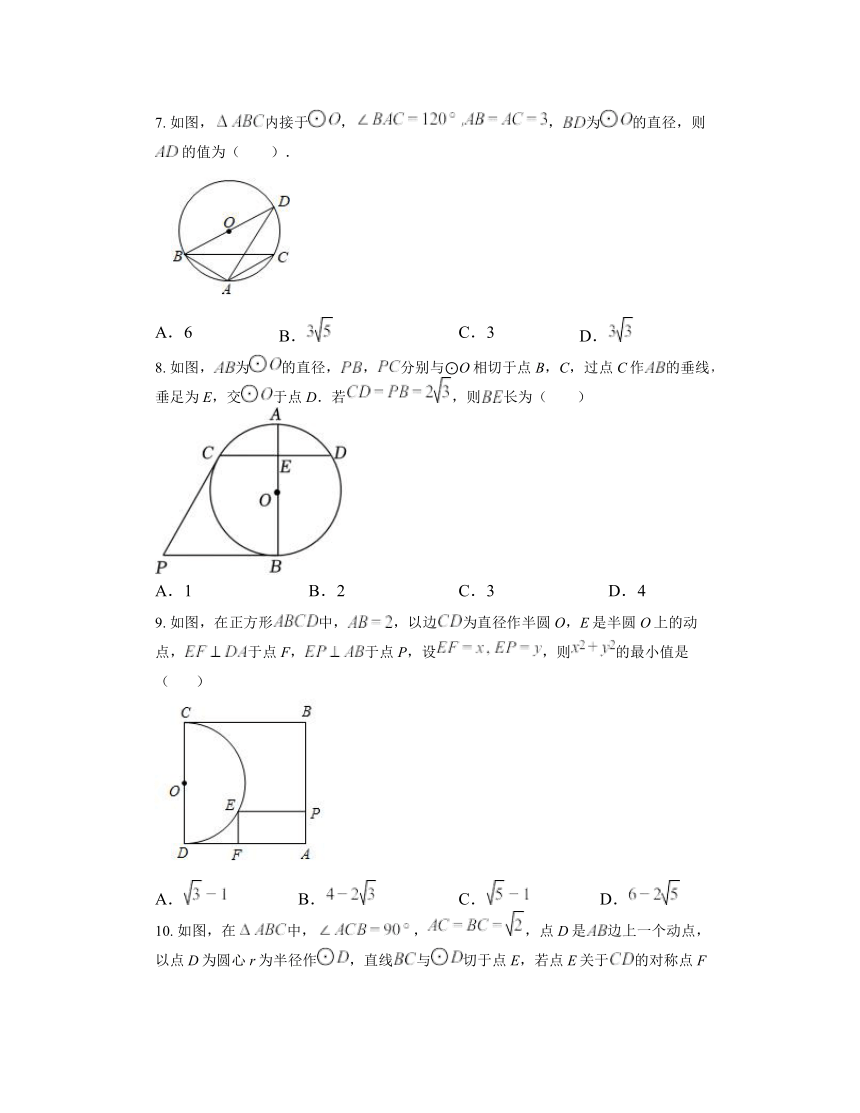
7. 如图,内接于,,为的直径,则 的值为( ).
A.6 B. C.3 D.
8. 如图,为的直径,,分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( )
A.1 B.2 C.3 D.4
9. 如图,在正方形中,,以边为直径作半圆O,E是半圆O上的动点,于点F,于点P,设,则的最小值是( )
A. B. C. D.
10. 如图,在中,,,点D是边上一个动点,以点D为圆心r为半径作,直线与切于点E,若点E关于的对称点F恰好落在边上,则r的值是( )
A. B.1 C. D.
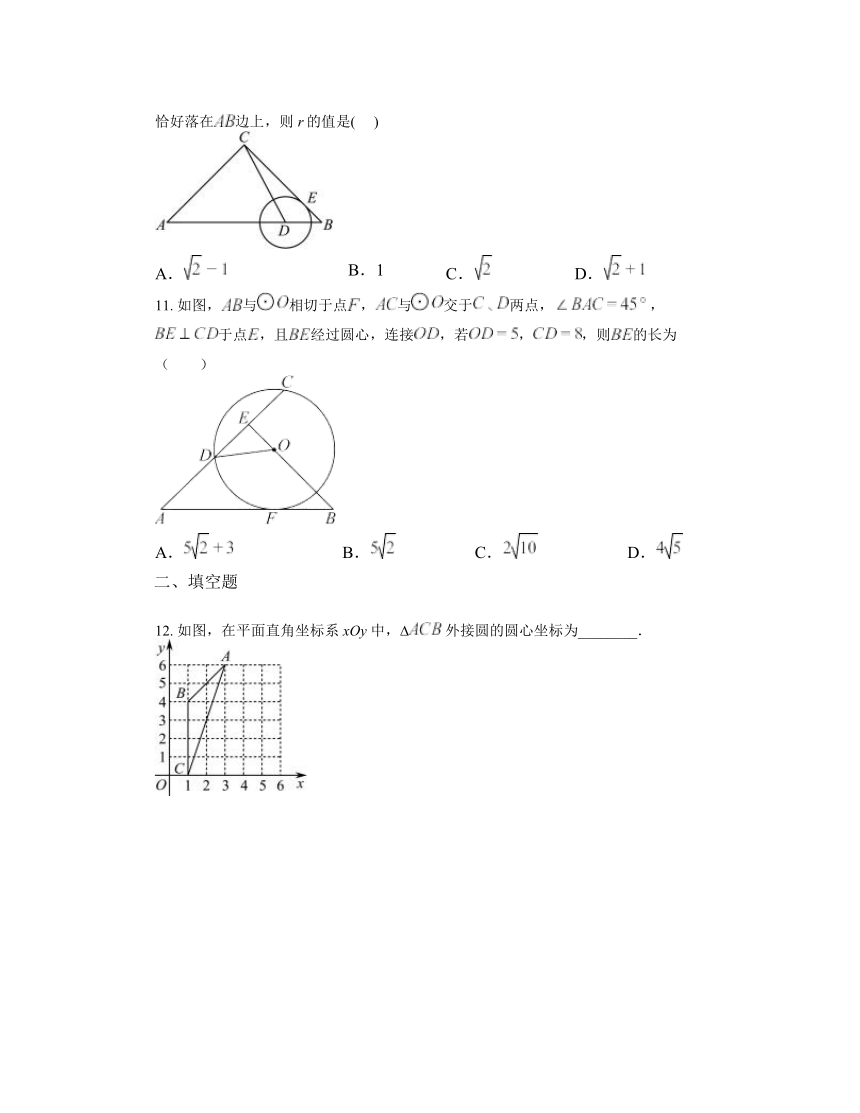
11. 如图,与相切于点,与交于两点,,于点,且经过圆心,连接,若,,则的长为( )
A. B. C. D.
二、填空题
12. 如图,在平面直角坐标系 xOy 中, 外接圆的圆心坐标为________.
13. 如图,在平面直角坐标系中,、、.
(1)经过、、三点的圆弧所在圆的圆心的坐标为______;
(2)这个圆的半径为______;
(3)点与的位置关系为点在______(填内、外、上).
14. 在如图所示的网格中,每个小正方形的边长都为1,点A,B,C均为格点,且都在同一个圆上.
(1)AB的长度等于________;
(2)请用无刻度的直尺在给定的网格中,画出圆的切线CD,并简要说明点D的位置是如何找到的.
____________________________________________________________.
15. 如图,点C在以AB为直径的半圆上,AB=8,∠ABC=30°,点D在线段AB上运动,点E与点D关于BC对称,DF⊥DE于点D,并交EC的延长线于点F,下列结论:
①CE=CF;②∠E=30°;③线段EF的最小值为2;④当AD=2时,EF与半圆相切.其中正确结论的序号是___________.
三、解答题
16. 如图,已知.
(1)尺规作图:作的外接圆;(不要求写作法)
(2)若,,求的外接圆半径是___________.
17. 如图,已知点是直线外一点,点是直线上一点,请用尺规作,使得过点且与直线l相切于点.(要求:尺规保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
18. 如图,是的外接圆,是的直径,过O作于点E,延长至点D,连接,使.
(1)求证:是的切线;
(2)若,求的长.
19. 如图,是的直径,直线与相切于点A,直线与相切于点,点(异于点)在上,点在上,且,延长与相交于点,连接并延长交于点.
(1)求证:是的切线;
(2)求证:.
20. 在平面直角坐标系中,圆的半径为1,对于和直线给出如下定义:若的一条边关于直线的对称线段,且、两点均在圆上,则称是圆的关于直线的“关联三角形”,直线是“关联轴”.
(1)如图1,若是圆的关于直线的“关联三角形”,请画出与圆的“关联轴”(至少画两条);
(2)如图2,若中,点坐标为,点坐标为,点在直线上,存在“关联轴”使是圆的关联三角形,写出点横坐标的取值范围:___________;
(3)已知,将点向上平移2个单位得到点,以为圆心为半径画圆,,为圆上的两点,且(点在点右侧),若与圆的关联轴至少有两条,直接写出的最小值和最大值,以及最大时的长.
一、选择题
1. 用反证法证明命题“在中,若,,则”时,首先应假设( )
A. B. C. D.
2. 下列命题中真命题的是( )
A.长度相等的弧是等弧 B.相等的圆心角所对的弦相等
C.任意三点确定一个圆 D.圆是中心对称图形,圆心是它的对称中心
3. 已知的半径为5,直线与有2个公共点,则点到直线的距离可能是( )
A.3 B.5 C.7 D.9
4. 如图,是两个同心圆中大圆的弦,且与小圆相切于点C,若两圆半径分别为和,则弦长为( )
A. B. C. D.
5. 已知圆半径为,,,为射线上的三个点,,,,则( )
A.点在内 B.点在上 C.点在外 D.点在上
6. 下列说法正确的是( )
A.等弧所对的圆心角相等 B.相等的弦所对的弧相等
C.过三点一定可以确定一个圆 D.垂直于半径的直线是圆的切线
7. 如图,内接于,,为的直径,则 的值为( ).
A.6 B. C.3 D.
8. 如图,为的直径,,分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( )
A.1 B.2 C.3 D.4
9. 如图,在正方形中,,以边为直径作半圆O,E是半圆O上的动点,于点F,于点P,设,则的最小值是( )
A. B. C. D.
10. 如图,在中,,,点D是边上一个动点,以点D为圆心r为半径作,直线与切于点E,若点E关于的对称点F恰好落在边上,则r的值是( )
A. B.1 C. D.
11. 如图,与相切于点,与交于两点,,于点,且经过圆心,连接,若,,则的长为( )
A. B. C. D.
二、填空题
12. 如图,在平面直角坐标系 xOy 中, 外接圆的圆心坐标为________.
13. 如图,在平面直角坐标系中,、、.
(1)经过、、三点的圆弧所在圆的圆心的坐标为______;
(2)这个圆的半径为______;
(3)点与的位置关系为点在______(填内、外、上).
14. 在如图所示的网格中,每个小正方形的边长都为1,点A,B,C均为格点,且都在同一个圆上.
(1)AB的长度等于________;
(2)请用无刻度的直尺在给定的网格中,画出圆的切线CD,并简要说明点D的位置是如何找到的.
____________________________________________________________.
15. 如图,点C在以AB为直径的半圆上,AB=8,∠ABC=30°,点D在线段AB上运动,点E与点D关于BC对称,DF⊥DE于点D,并交EC的延长线于点F,下列结论:
①CE=CF;②∠E=30°;③线段EF的最小值为2;④当AD=2时,EF与半圆相切.其中正确结论的序号是___________.
三、解答题
16. 如图,已知.
(1)尺规作图:作的外接圆;(不要求写作法)
(2)若,,求的外接圆半径是___________.
17. 如图,已知点是直线外一点,点是直线上一点,请用尺规作,使得过点且与直线l相切于点.(要求:尺规保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
18. 如图,是的外接圆,是的直径,过O作于点E,延长至点D,连接,使.
(1)求证:是的切线;
(2)若,求的长.
19. 如图,是的直径,直线与相切于点A,直线与相切于点,点(异于点)在上,点在上,且,延长与相交于点,连接并延长交于点.
(1)求证:是的切线;
(2)求证:.
20. 在平面直角坐标系中,圆的半径为1,对于和直线给出如下定义:若的一条边关于直线的对称线段,且、两点均在圆上,则称是圆的关于直线的“关联三角形”,直线是“关联轴”.
(1)如图1,若是圆的关于直线的“关联三角形”,请画出与圆的“关联轴”(至少画两条);
(2)如图2,若中,点坐标为,点坐标为,点在直线上,存在“关联轴”使是圆的关联三角形,写出点横坐标的取值范围:___________;
(3)已知,将点向上平移2个单位得到点,以为圆心为半径画圆,,为圆上的两点,且(点在点右侧),若与圆的关联轴至少有两条,直接写出的最小值和最大值,以及最大时的长.
同课章节目录
