专题1.15勾股定理(全章复习与巩固)分层练习提升篇(含解析)2023-2024学年八年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.15勾股定理(全章复习与巩固)分层练习提升篇(含解析)2023-2024学年八年级数学上册北师大版专项讲练 |
|
|
| 格式 | docx | ||
| 文件大小 | 958.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览

文档简介
专题1.15 勾股定理(全章复习与巩固)(分层练习)(提升篇)
一、单选题
1.下列各组数为勾股数的是( )
A. B. C. D.
2.直角三角形两直角边长度为5,12,则斜边上的高为( )
A.6 B.8 C.13 D.
3.在中,,是延长线上一点,,是上一点,连接交于点,若,,则ED的长为( )
A.2.5 B.4.5 C.8.5 D.10
4.如图,长方形中,,,将此长方形折叠,使点D与点B重合,折痕为.则的长为( )
A.13 B.12 C.10 D.8
5.如图,在中,,,以点A为圆心,长为半径画弧,交线段于点D;以B为圆心,长为半径画弧,交线段于点E.若,则的长为( )
A. B. C. D.
6.在中,,,.以A为圆心,的长为半径作弧,分别交于点M、N,再分别以M、N为圆心,适当长度为半径画弧,两弧交于点P.连接,并延长交于D.过D作于点E,垂足为E,则的长度为()
A. B. C.2 D.1
7.如图,在直线m上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是,,,,则=( )
A.6 B.6.5 C.7 D.8
8.如图,在△ABC中,AC=3 cm,BC=4 cm,AB=5 cm,D,E,F分别是AB,BC,CA的中点,则△DEF的面积等于( )
A.1 B.1.5 C.2 D.3
9.如图,长为的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升到D点,则橡皮筋被拉长了( )
A. B. C. D.
10.我国古代数学专著《九章算术》里记载了这样一个问题“今有垣高一丈.倚木于垣,上与垣齐,引木却行一尺,其木至地.问木长几何?”其内容可以表述为:“有一面墙,高1丈,将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上,问木杆长多少尺?”(说明:1丈尺),此木杆的长度为( )
A.49尺 B.49.5尺 C.50尺 D.50.5尺
二、填空题
11.已知△ABC中,AB=6cm,BC=8cm,AC=10cm,则△ABC的面积是 cm2.
12.如图,在方格中,小正方形的边长均为1,则图中阴影正方形的边长是 .
13.如图,三角形中,,,,P为直线上一动点,连接,则线段的最小值是 .
14.如图,在中,,,,D为BC边上一点将沿AD折叠,若点B恰好落在线段AC的延长线上点E处,则CD的长为 .
15.如图,四个全等的直角三角形围成一个大正方形,中间阴影部分是一个小正方形,这样就组成一个“赵爽弦图”.若,则正方形的面积为 .
16.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度为 cm(容器壁厚度忽略不计).
17.如图,长方形中,,E为边上的动点,F为的中点,连接,则的最小值为
18.如图,在直角三角形纸片中,,,,沿将纸片折叠,使点落在边上的点处,再折叠纸片,使点与点重合,折痕分别与,交于点,,连接,则的长为 .
三、解答题
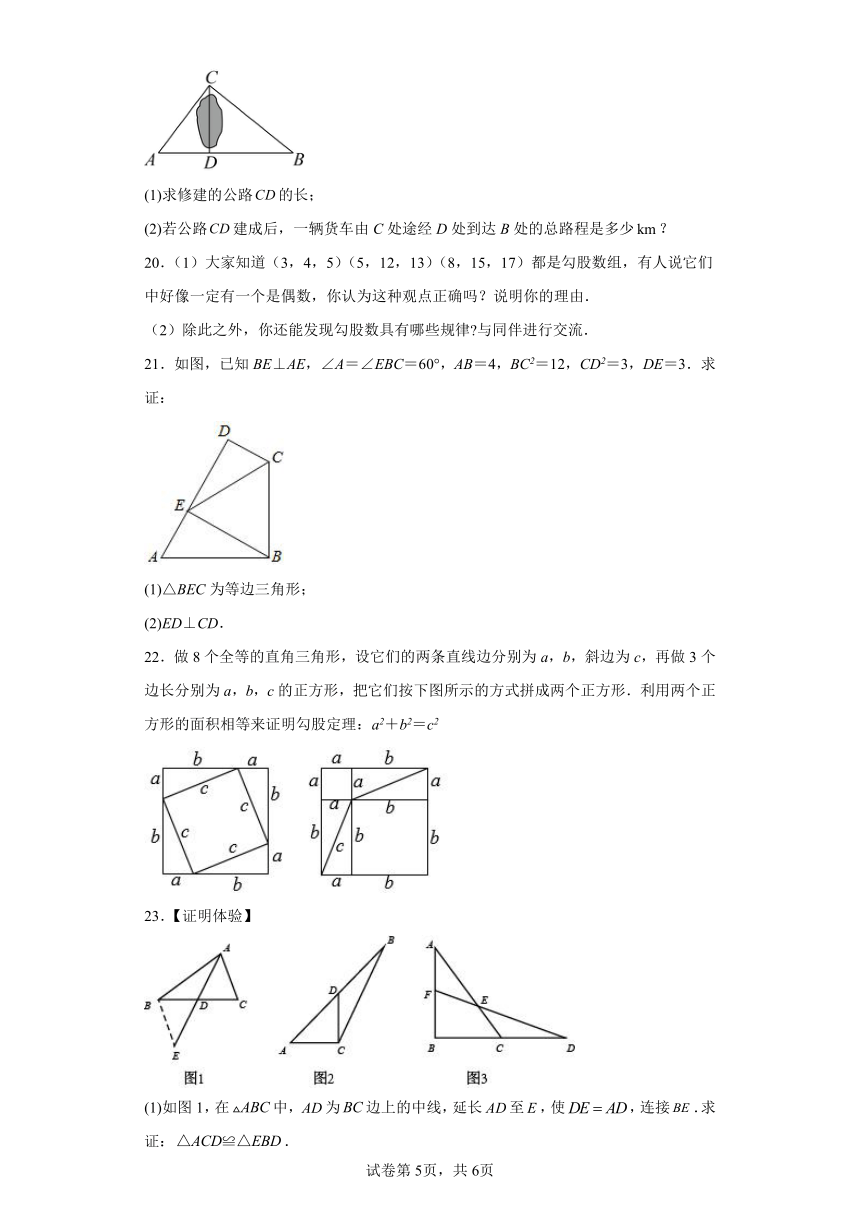
19.如图,在笔直的公路旁有一座山,为方便运输货物现要从公路上的D处开凿隧道通一条公路到C处,已知点C与公路上的停靠站A的距离为,与公路上另一停靠站B的距离为,且,.
(1)求修建的公路的长;
(2)若公路建成后,一辆货车由C处途经D处到达B处的总路程是多少?
20.(1)大家知道(3,4,5)(5,12,13)(8,15,17)都是勾股数组,有人说它们中好像一定有一个是偶数,你认为这种观点正确吗?说明你的理由.
(2)除此之外,你还能发现勾股数具有哪些规律 与同伴进行交流.
21.如图,已知BE⊥AE,∠A=∠EBC=60°,AB=4,BC2=12,CD2=3,DE=3.求证:
(1)△BEC为等边三角形;
(2)ED⊥CD.
22.做8个全等的直角三角形,设它们的两条直线边分别为a,b,斜边为c,再做3个边长分别为a,b,c的正方形,把它们按下图所示的方式拼成两个正方形.利用两个正方形的面积相等来证明勾股定理:a2+b2=c2
23.【证明体验】
(1)如图1,在中,为边上的中线,延长至,使,连接.求证:.
【迁移应用】
(2)如图2,在中,,,为的中点,.求面积.
【拓展延伸】
(3)如图3,在中,,是延长线上一点,,是上一点,连接交于点,若,,求的长.
24.在矩形ABCD中,AB=6,BC=8,点E是射线BC上一个动点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折到△AB'E,延长AB'与直线CD交于点M.
(1)求证:AM=MF;
(2)当点E是边BC的中点时,求CM的长;
(3)当CF=4时,求CM的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据勾股数的定义:满足的三个正整数,称为勾股数判定则可.
【详解】解:A.,不能构成直角三角形,故不是勾股数;
B.,能构成直角三角形,是正整数,故是勾股数;
C.,不能构成直角三角形,故不是勾股数;
D.,不能构成直角三角形,故不是勾股数.
故选:B.
【点睛】本题考查了勾股数的定义,注意:一组勾股数必须同时满足两个条件:①三个数都是正整数;②两个较小数的平方和等于最大数的平方.
2.D
【分析】利用勾股定理和等积法进行求解即可.
【详解】解:由题意得:
直角三角形的斜边长为:,
设斜边上的高为:,
由直角三角形的面积相等可得:,
解得:;
故选D.
【点睛】本题考查的勾股定理的应用,求直角三角形斜边上的高.熟练掌握等积法是解题的关键.
3.B
【分析】延长到,使得,连接.证明,得到,,结合已知证明,设,则,,在中,根据,构建方程即可解决问题.
【详解】解:延长到,使得,连接.
在和中,
,
∴,
,,
,
,
,
,
,
设,则,,
在中,,
,
,
.
【点睛】本题属考查了全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
4.A
【分析】设为x,则为,在由勾股定理有,即可求得.
【详解】解:由折叠的性质可知,
设为x,则为,
∵四边形为长方形
∴,
∴在中由勾股定理有
即
化简得
解得,
故选:A.
【点睛】本题考查了折叠问题求折痕或其他边长,主要可根据折叠前后两图形的全等条件,把某个直角三角形的三边都用同一未知量表示出来,并根据勾股定理建立方程,进而可以求解.
5.A
【分析】设根据,在中,由勾股定理列出方程即可求解.
【详解】解:设,
∵,,
∴,
在中,,
∴为直角三角形,
在中,由勾股定理得:,
解得:,
即
故选:A.
【点睛】本题主要考查了勾股定理,解题的关键是根据题意得出,进而表示出的长.
6.A
【分析】直接利用基本作图方法得出:,再利用全等三角形的判定与性质得出,结合勾股定理得出答案.
【详解】解:如图所示:由题意可得:,
在和中,
设,
则,
故,
解得∶.
故选:A.
【点睛】此题主要考查了基本作图以及全等三角形的判定与性质、勾股定理等知识,正确应用勾股定理是解题关键.
7.A
【分析】运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
【详解】解:如图,观察发现,
∵,
∴,,
∴,
在与中,,
∴(AAS),
∴,
∵,
∴,
即,
同理,,
则,
则.
故选:A.
【点睛】此题考查了全等三角形的判定以及性质、勾股定理.解决本题的关键是得到.
8.B
【分析】由三角形中位线的性质易得△DEF的三边长,再由勾股定理的逆定理证出△DEF是直角三角形,然后由三角形面积公式求解即可.
【详解】解:∵D,E,F分别是AB,BC,CA的中点
∴EF,DE,DF都是△ABC的中位线,
∴EF=AB,DE=AC,DF=BC,
又∵AB=5cm,BC=4cm,AC=3cm,
∴EF=2.5(cm),DE=2(cm),DF=1.5(cm),
∵1.52+22=2.52,
∴DE2+DF2=EF2,
∴△EDF为直角三角形,
∴S△EDF=DE DF=×1.5×2=1.5(cm2),
故选:B.
【点睛】本题考查了三角形中位线定理、勾股定理的逆定理等知识;熟练掌握三角形中位线定理,由勾股定理的逆定理证出△DEF为直角三角形是解题的关键.
9.A
【分析】根据勾股定理,可求出AD长,再证明△ADC≌△BDC(SAS),可得AD=BD=5cm,求出AD+BD-AB即为橡皮筋拉长的距离.
【详解】解:点C为线段AB的中点,
∴AC=AB=4cm,
Rt△ACD中, CD=3cm;
根据勾股定理,得:AD==5(cm);
∵CD⊥AB,
∴∠DCA=∠DCB=90°,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴AD=BD=5cm,
∴AD+BD-AB=2AD-AB=10-8=2cm;
∴橡皮筋被拉长了2cm.
故选:A.
【点睛】本题主要考查了勾股定理的应用,三角形全等判定与性质,线段中点定义,解题的关键是勾股定理的应用,三角形全等判定与性质,线段中点定义,灵活运用所学知识解决问题.
10.D
【分析】当木杆的上端与墙头平齐时,木杆与墙、地面构成直角三角形,设木杆长为尺,则木杆底端离墙有尺,根据勾股定理可列出方程,解方程即可
【详解】如图,设木杆长为尺,则木杆底端B离墙的距离即的长有尺,
在中,
∵,
∴,
解得:
故选:D.
【点睛】本题考查了勾股定理的应用,解题的关键是由实际问题抽象出直角三角形,从而运用勾股定理解题.
11.24
【分析】由勾股定理的逆定理得出△ABC是直角三角形,∠B=90°,△ABC的面职为即可得出结果.
【详解】解:∵AB=6cm,BC=8cm,AC=10cm,
∴AB2+CB2=100=AC2,
∴△ABC是直角三角形,且∠B=90°,
∴△ABC的面积是==24(cm2),
故答案为:24.
【点睛】本题考查了勾股定理的逆定理,直角三角形面积的计算方法,熟练掌握勾股定理的逆定理,并能进行推理论证与计算是解决问题的关键.
12.5
【分析】根据网格构造直角三角形,由勾股定理可得答案.
【详解】解:如图,在中,,,
,
故答案为:5.
【点睛】本题考查了勾股定理,根据网格构造直角三角形是解决问题的关键.
13.
【分析】当时,的值最小,利用等面积法求解即可.
【详解】解:在中,,,,
∴,
∵点到直线,垂线段最短,
∴当时,的值最小,
此时:,即:,
∴,
故答案为.
【点睛】本题考查垂线段最短.熟练掌握点到直线,垂线段最短,利用等积法求斜边上的高,是解题的关键.
14.3
【分析】根据勾股定理可以得到AC的长,然后根据翻折的性质和勾股定理,即可求得CD的长.
【详解】解:∵∠ACB=90°,AB=10,BC=8,
∵将△ABD沿AD折叠,点B恰好落在线段AC的延长线上点E处,
∴AE=AB=10,BD=ED,
∴CE=AE-AC=10-6=4,
设CD=x,则BD=8-x,
∵∠DCE=90°,
∴CD2+CE2=ED2,
即,
解得x=3,
∴CD=3,
故答案为:3.
【点睛】本题考查了勾股定理与折叠问题,掌握勾股定理是解题的关键.
15.4
【分析】利用勾股定理求得直角边的较短边,进一步根据正方形EFGH的面积=大正方形面积-4个直角三角形面积即可求得正方形EFGH的面积.
【详解】解:直角三角形直角边的较短边为=6,
正方形EFGH的面积=10×10-8×6÷2×4=100-96=4.
故答案为:4.
【点睛】此题考查勾股定理的运用,掌握勾股定理的推导过程是解决问题的关键.
16.34
【分析】首先展开圆柱的侧面,即是矩形,接下来根据两点之间线段最短,可知CF的长即为所求;然后结合已知条件求出DF与CD的长,再利用勾股定理进行计算即可.
【详解】如图为圆柱形玻璃容器的侧面展开图,线段CF是蜘蛛由C到F的最短路程.
根据题意,可知DF=18-1-1=16(cm),CD(cm),
∴(cm),
即蜘蛛所走的最短路线的长度是34cm.
故答案为34.
【点睛】此题是有关最短路径的问题,关键在于把立体图形展开成平面图形,找出最短路径;
17.15
【分析】作F关于的对称点,连接,交于点E,则,的长即为的最小值.运用勾股定理求即可.
【详解】
如图:作F关于的对称点,连接,交于点E,则,的长即为的最小值.
长方形中,,F为的中点,
∴,
∴,
∴,
即的最小值为15.
故答案为:15.
【点睛】本题主要考查轴对称的性质及运用,能够熟练掌握并运用将军饮马模型是解题关键.
18.
【分析】根据沿过点A的直线将纸片折叠,使点B落在边上的点处,得,,又再折叠纸片,使点与点重合,得,,即可得,,设,则,可得,即可解得.
【详解】解:沿将纸片折叠,使点B落在边上的点处,
,,
折叠纸片,使点与点重合,
,,
,
,
,
,
,
设,则,
,
解得,
,
故答案为:.
【点睛】本题考查了直角三角形中的翻折变换,勾股定理,一元一次方程解法,完全平方公式,解题的关键是掌握翻折的性质,熟练利用勾股定理列方程.
19.(1)修建的公路CD的长为
(2)总路程为
【分析】(1)根据题意可得:,,,利用勾股定理可得,再由三角形的等面积法计算即可得出;
(2)由垂直的性质及(1)中结论,再利用勾股定理可得出长度,然后求长即可.
【详解】(1)解:∵,
∴,
根据题意可得:,,
∴,
,
∴,
∴,
∴修建的公路CD的长为;
(2)解:∵,
∴,
根据题意可得:,,
∴,
∴,
∴总路程为.
【点睛】本题主要考查勾股定理的应用,理解题意,熟练应用勾股定理是解题关键.
20.(1)正确,见解析;(2)见解析
【分析】(1)根据奇数的平方是奇数,偶数的平方是偶数,奇数加奇数为偶数即可判断;
(2)发现当勾股数组中较大的两个数为连续整数时,最小数的平方为奇数.
【详解】(1)勾股数中一定有一个是偶数,
如果全部为奇数,为偶数,而为奇数,两者不可能相等,
即一定存在一个偶数.
(2)勾股数组中较大的两个数为连续整数时,最小数的平方为奇数,
理由如下:
不妨令最大整数为,跟它连续的整数为,
根据勾股定理有,
,
即最小数的平方为奇数.
【点睛】本题考查了勾股定理,解题的关键是掌握偶数的平方是偶数,奇数的平方是奇数,奇数加奇数是偶数.
21.(1)见解析
(2)见解析
【分析】(1)在Rt△ABE中,求得AE=2,BE2=12,从而有BE=BC,即可得出△BEC为等边三角形;
(2)求得DE2+CD2=12=EC2,所以△CDE为直角三角形,且∠D=90°,即可解决问题.
【详解】(1)证明:根据题意可得:在Rt△ABE中,
∵∠A=60°,∠AEB=90°,
∴∠ABE=30°.
∵AB=4,
∴AE=AB=2,BE2=AB2﹣AE2=12.
又∵BC2=12,
∴BE=BC.
又∵∠CBE=60°,
∴△BEC为等边三角形.
(2)∵△BEC为等边三角形,
∴EC2=BC2=12.
又∵DE2=9,CD2=3,
∴DE2+CD2=12=EC2,
∴△CDE为直角三角形,且∠D=90°,
∴ED⊥CD.
【点睛】本题主要考查了等边三角形的判定与性质、勾股定理和其逆定理,熟练运用勾股定理的逆定理是解题的关键.
22.证明见解析
【分析】根据不同图形拼成的两个正方形面积相等即可证明
【详解】证明:①左图大正方形的边长为:a+b,则面积为(a+b)2,分成了四个直角边为a,b,斜边为c的全等的直角三角形和一个边长为c的小正方形,
;
②右图大正方形的边长为:a+b,则面积为(a+b)2,分成了边长为a的一个正方形,边长为b的一个正方形,还有四个直角边为a,b,斜边为c的全等的直角三角形,
;
综上所述:,即.
【点睛】本题考查利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长的关系进行组合图形.
23.(1)见解析
(2)
(3)的长为
【分析】(1)根据证明三角形全等;
(2)如图2中,延长到,使得,连接.由(1)可知,推出,,利用勾股定理求出,即可解决问题;
(3)如图3中,延长到,使得,连接.证明,设,则,,在中,根据,构建方程即可解决问题.
【详解】(1)证明:如图1中,
在和中,
,
;
(2)解:如图2中,延长到,使得,连接.
由(1)可知,
,,
,
,
;
(3)解:如图3中,延长到,使得,连接.
由(1)可知,,
,,
,
,
,
,
,
设,则,,
在中,,
,
,
.
【点睛】本题属于三角形综合题,考查了全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
24.(1)见解析
(2)
(3)或 21
【分析】(1)由折叠的性质及等腰三角形的判定可得出答案;
(2)利用矩形的性质证得,根据全等三角形的性质得到,设,则由(1)知,, ,在中利用勾股定理即可求解;
(3)当时,设,应分两种情况:第一种情况,点在线段上,如图所示,则,;
第二种情况,点在线段上,如图所示,则,
在中,利用勾股定理即可求解.
【详解】(1)证明:∵四边形ABCD为矩形,
∴ABCD,
∴∠F=∠BAF,
由折叠可知:∠BAF=∠MAF,
∴∠F=∠MAF,
∴AM=MF;
(2)∵点E是边BC的中点,
∴,
∵四边形ABCD为矩形,,
∴ABCD,,
∴∠F=∠BAF,
又∵,
∴,
∴,
设,则由(1)知,,
在中,,
∴,
解得,
∴的长为;
(3)当时,设,应分两种情况:
第一种情况,点在线段上,如图所示,则,
∴在中,,
∴,
解得,
∴的长为;
第二种情况,点在线段的延长线上,如图所示,则,
∴在中,,
∴,解得,
∴的长为
综上可知,当CF=4时,CM的长为或 21
【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,分类讨论的思想是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列各组数为勾股数的是( )
A. B. C. D.
2.直角三角形两直角边长度为5,12,则斜边上的高为( )
A.6 B.8 C.13 D.
3.在中,,是延长线上一点,,是上一点,连接交于点,若,,则ED的长为( )
A.2.5 B.4.5 C.8.5 D.10
4.如图,长方形中,,,将此长方形折叠,使点D与点B重合,折痕为.则的长为( )
A.13 B.12 C.10 D.8
5.如图,在中,,,以点A为圆心,长为半径画弧,交线段于点D;以B为圆心,长为半径画弧,交线段于点E.若,则的长为( )
A. B. C. D.
6.在中,,,.以A为圆心,的长为半径作弧,分别交于点M、N,再分别以M、N为圆心,适当长度为半径画弧,两弧交于点P.连接,并延长交于D.过D作于点E,垂足为E,则的长度为()
A. B. C.2 D.1
7.如图,在直线m上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是3,6,9,正放置的四个正方形的面积依次是,,,,则=( )
A.6 B.6.5 C.7 D.8
8.如图,在△ABC中,AC=3 cm,BC=4 cm,AB=5 cm,D,E,F分别是AB,BC,CA的中点,则△DEF的面积等于( )
A.1 B.1.5 C.2 D.3
9.如图,长为的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升到D点,则橡皮筋被拉长了( )
A. B. C. D.
10.我国古代数学专著《九章算术》里记载了这样一个问题“今有垣高一丈.倚木于垣,上与垣齐,引木却行一尺,其木至地.问木长几何?”其内容可以表述为:“有一面墙,高1丈,将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上,问木杆长多少尺?”(说明:1丈尺),此木杆的长度为( )
A.49尺 B.49.5尺 C.50尺 D.50.5尺
二、填空题
11.已知△ABC中,AB=6cm,BC=8cm,AC=10cm,则△ABC的面积是 cm2.
12.如图,在方格中,小正方形的边长均为1,则图中阴影正方形的边长是 .
13.如图,三角形中,,,,P为直线上一动点,连接,则线段的最小值是 .
14.如图,在中,,,,D为BC边上一点将沿AD折叠,若点B恰好落在线段AC的延长线上点E处,则CD的长为 .
15.如图,四个全等的直角三角形围成一个大正方形,中间阴影部分是一个小正方形,这样就组成一个“赵爽弦图”.若,则正方形的面积为 .
16.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度为 cm(容器壁厚度忽略不计).
17.如图,长方形中,,E为边上的动点,F为的中点,连接,则的最小值为
18.如图,在直角三角形纸片中,,,,沿将纸片折叠,使点落在边上的点处,再折叠纸片,使点与点重合,折痕分别与,交于点,,连接,则的长为 .
三、解答题
19.如图,在笔直的公路旁有一座山,为方便运输货物现要从公路上的D处开凿隧道通一条公路到C处,已知点C与公路上的停靠站A的距离为,与公路上另一停靠站B的距离为,且,.
(1)求修建的公路的长;
(2)若公路建成后,一辆货车由C处途经D处到达B处的总路程是多少?
20.(1)大家知道(3,4,5)(5,12,13)(8,15,17)都是勾股数组,有人说它们中好像一定有一个是偶数,你认为这种观点正确吗?说明你的理由.
(2)除此之外,你还能发现勾股数具有哪些规律 与同伴进行交流.
21.如图,已知BE⊥AE,∠A=∠EBC=60°,AB=4,BC2=12,CD2=3,DE=3.求证:
(1)△BEC为等边三角形;
(2)ED⊥CD.
22.做8个全等的直角三角形,设它们的两条直线边分别为a,b,斜边为c,再做3个边长分别为a,b,c的正方形,把它们按下图所示的方式拼成两个正方形.利用两个正方形的面积相等来证明勾股定理:a2+b2=c2
23.【证明体验】
(1)如图1,在中,为边上的中线,延长至,使,连接.求证:.
【迁移应用】
(2)如图2,在中,,,为的中点,.求面积.
【拓展延伸】
(3)如图3,在中,,是延长线上一点,,是上一点,连接交于点,若,,求的长.
24.在矩形ABCD中,AB=6,BC=8,点E是射线BC上一个动点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折到△AB'E,延长AB'与直线CD交于点M.
(1)求证:AM=MF;
(2)当点E是边BC的中点时,求CM的长;
(3)当CF=4时,求CM的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据勾股数的定义:满足的三个正整数,称为勾股数判定则可.
【详解】解:A.,不能构成直角三角形,故不是勾股数;
B.,能构成直角三角形,是正整数,故是勾股数;
C.,不能构成直角三角形,故不是勾股数;
D.,不能构成直角三角形,故不是勾股数.
故选:B.
【点睛】本题考查了勾股数的定义,注意:一组勾股数必须同时满足两个条件:①三个数都是正整数;②两个较小数的平方和等于最大数的平方.
2.D
【分析】利用勾股定理和等积法进行求解即可.
【详解】解:由题意得:
直角三角形的斜边长为:,
设斜边上的高为:,
由直角三角形的面积相等可得:,
解得:;
故选D.
【点睛】本题考查的勾股定理的应用,求直角三角形斜边上的高.熟练掌握等积法是解题的关键.
3.B
【分析】延长到,使得,连接.证明,得到,,结合已知证明,设,则,,在中,根据,构建方程即可解决问题.
【详解】解:延长到,使得,连接.
在和中,
,
∴,
,,
,
,
,
,
,
设,则,,
在中,,
,
,
.
【点睛】本题属考查了全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
4.A
【分析】设为x,则为,在由勾股定理有,即可求得.
【详解】解:由折叠的性质可知,
设为x,则为,
∵四边形为长方形
∴,
∴在中由勾股定理有
即
化简得
解得,
故选:A.
【点睛】本题考查了折叠问题求折痕或其他边长,主要可根据折叠前后两图形的全等条件,把某个直角三角形的三边都用同一未知量表示出来,并根据勾股定理建立方程,进而可以求解.
5.A
【分析】设根据,在中,由勾股定理列出方程即可求解.
【详解】解:设,
∵,,
∴,
在中,,
∴为直角三角形,
在中,由勾股定理得:,
解得:,
即
故选:A.
【点睛】本题主要考查了勾股定理,解题的关键是根据题意得出,进而表示出的长.
6.A
【分析】直接利用基本作图方法得出:,再利用全等三角形的判定与性质得出,结合勾股定理得出答案.
【详解】解:如图所示:由题意可得:,
在和中,
设,
则,
故,
解得∶.
故选:A.
【点睛】此题主要考查了基本作图以及全等三角形的判定与性质、勾股定理等知识,正确应用勾股定理是解题关键.
7.A
【分析】运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
【详解】解:如图,观察发现,
∵,
∴,,
∴,
在与中,,
∴(AAS),
∴,
∵,
∴,
即,
同理,,
则,
则.
故选:A.
【点睛】此题考查了全等三角形的判定以及性质、勾股定理.解决本题的关键是得到.
8.B
【分析】由三角形中位线的性质易得△DEF的三边长,再由勾股定理的逆定理证出△DEF是直角三角形,然后由三角形面积公式求解即可.
【详解】解:∵D,E,F分别是AB,BC,CA的中点
∴EF,DE,DF都是△ABC的中位线,
∴EF=AB,DE=AC,DF=BC,
又∵AB=5cm,BC=4cm,AC=3cm,
∴EF=2.5(cm),DE=2(cm),DF=1.5(cm),
∵1.52+22=2.52,
∴DE2+DF2=EF2,
∴△EDF为直角三角形,
∴S△EDF=DE DF=×1.5×2=1.5(cm2),
故选:B.
【点睛】本题考查了三角形中位线定理、勾股定理的逆定理等知识;熟练掌握三角形中位线定理,由勾股定理的逆定理证出△DEF为直角三角形是解题的关键.
9.A
【分析】根据勾股定理,可求出AD长,再证明△ADC≌△BDC(SAS),可得AD=BD=5cm,求出AD+BD-AB即为橡皮筋拉长的距离.
【详解】解:点C为线段AB的中点,
∴AC=AB=4cm,
Rt△ACD中, CD=3cm;
根据勾股定理,得:AD==5(cm);
∵CD⊥AB,
∴∠DCA=∠DCB=90°,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴AD=BD=5cm,
∴AD+BD-AB=2AD-AB=10-8=2cm;
∴橡皮筋被拉长了2cm.
故选:A.
【点睛】本题主要考查了勾股定理的应用,三角形全等判定与性质,线段中点定义,解题的关键是勾股定理的应用,三角形全等判定与性质,线段中点定义,灵活运用所学知识解决问题.
10.D
【分析】当木杆的上端与墙头平齐时,木杆与墙、地面构成直角三角形,设木杆长为尺,则木杆底端离墙有尺,根据勾股定理可列出方程,解方程即可
【详解】如图,设木杆长为尺,则木杆底端B离墙的距离即的长有尺,
在中,
∵,
∴,
解得:
故选:D.
【点睛】本题考查了勾股定理的应用,解题的关键是由实际问题抽象出直角三角形,从而运用勾股定理解题.
11.24
【分析】由勾股定理的逆定理得出△ABC是直角三角形,∠B=90°,△ABC的面职为即可得出结果.
【详解】解:∵AB=6cm,BC=8cm,AC=10cm,
∴AB2+CB2=100=AC2,
∴△ABC是直角三角形,且∠B=90°,
∴△ABC的面积是==24(cm2),
故答案为:24.
【点睛】本题考查了勾股定理的逆定理,直角三角形面积的计算方法,熟练掌握勾股定理的逆定理,并能进行推理论证与计算是解决问题的关键.
12.5
【分析】根据网格构造直角三角形,由勾股定理可得答案.
【详解】解:如图,在中,,,
,
故答案为:5.
【点睛】本题考查了勾股定理,根据网格构造直角三角形是解决问题的关键.
13.
【分析】当时,的值最小,利用等面积法求解即可.
【详解】解:在中,,,,
∴,
∵点到直线,垂线段最短,
∴当时,的值最小,
此时:,即:,
∴,
故答案为.
【点睛】本题考查垂线段最短.熟练掌握点到直线,垂线段最短,利用等积法求斜边上的高,是解题的关键.
14.3
【分析】根据勾股定理可以得到AC的长,然后根据翻折的性质和勾股定理,即可求得CD的长.
【详解】解:∵∠ACB=90°,AB=10,BC=8,
∵将△ABD沿AD折叠,点B恰好落在线段AC的延长线上点E处,
∴AE=AB=10,BD=ED,
∴CE=AE-AC=10-6=4,
设CD=x,则BD=8-x,
∵∠DCE=90°,
∴CD2+CE2=ED2,
即,
解得x=3,
∴CD=3,
故答案为:3.
【点睛】本题考查了勾股定理与折叠问题,掌握勾股定理是解题的关键.
15.4
【分析】利用勾股定理求得直角边的较短边,进一步根据正方形EFGH的面积=大正方形面积-4个直角三角形面积即可求得正方形EFGH的面积.
【详解】解:直角三角形直角边的较短边为=6,
正方形EFGH的面积=10×10-8×6÷2×4=100-96=4.
故答案为:4.
【点睛】此题考查勾股定理的运用,掌握勾股定理的推导过程是解决问题的关键.
16.34
【分析】首先展开圆柱的侧面,即是矩形,接下来根据两点之间线段最短,可知CF的长即为所求;然后结合已知条件求出DF与CD的长,再利用勾股定理进行计算即可.
【详解】如图为圆柱形玻璃容器的侧面展开图,线段CF是蜘蛛由C到F的最短路程.
根据题意,可知DF=18-1-1=16(cm),CD(cm),
∴(cm),
即蜘蛛所走的最短路线的长度是34cm.
故答案为34.
【点睛】此题是有关最短路径的问题,关键在于把立体图形展开成平面图形,找出最短路径;
17.15
【分析】作F关于的对称点,连接,交于点E,则,的长即为的最小值.运用勾股定理求即可.
【详解】
如图:作F关于的对称点,连接,交于点E,则,的长即为的最小值.
长方形中,,F为的中点,
∴,
∴,
∴,
即的最小值为15.
故答案为:15.
【点睛】本题主要考查轴对称的性质及运用,能够熟练掌握并运用将军饮马模型是解题关键.
18.
【分析】根据沿过点A的直线将纸片折叠,使点B落在边上的点处,得,,又再折叠纸片,使点与点重合,得,,即可得,,设,则,可得,即可解得.
【详解】解:沿将纸片折叠,使点B落在边上的点处,
,,
折叠纸片,使点与点重合,
,,
,
,
,
,
,
设,则,
,
解得,
,
故答案为:.
【点睛】本题考查了直角三角形中的翻折变换,勾股定理,一元一次方程解法,完全平方公式,解题的关键是掌握翻折的性质,熟练利用勾股定理列方程.
19.(1)修建的公路CD的长为
(2)总路程为
【分析】(1)根据题意可得:,,,利用勾股定理可得,再由三角形的等面积法计算即可得出;
(2)由垂直的性质及(1)中结论,再利用勾股定理可得出长度,然后求长即可.
【详解】(1)解:∵,
∴,
根据题意可得:,,
∴,
,
∴,
∴,
∴修建的公路CD的长为;
(2)解:∵,
∴,
根据题意可得:,,
∴,
∴,
∴总路程为.
【点睛】本题主要考查勾股定理的应用,理解题意,熟练应用勾股定理是解题关键.
20.(1)正确,见解析;(2)见解析
【分析】(1)根据奇数的平方是奇数,偶数的平方是偶数,奇数加奇数为偶数即可判断;
(2)发现当勾股数组中较大的两个数为连续整数时,最小数的平方为奇数.
【详解】(1)勾股数中一定有一个是偶数,
如果全部为奇数,为偶数,而为奇数,两者不可能相等,
即一定存在一个偶数.
(2)勾股数组中较大的两个数为连续整数时,最小数的平方为奇数,
理由如下:
不妨令最大整数为,跟它连续的整数为,
根据勾股定理有,
,
即最小数的平方为奇数.
【点睛】本题考查了勾股定理,解题的关键是掌握偶数的平方是偶数,奇数的平方是奇数,奇数加奇数是偶数.
21.(1)见解析
(2)见解析
【分析】(1)在Rt△ABE中,求得AE=2,BE2=12,从而有BE=BC,即可得出△BEC为等边三角形;
(2)求得DE2+CD2=12=EC2,所以△CDE为直角三角形,且∠D=90°,即可解决问题.
【详解】(1)证明:根据题意可得:在Rt△ABE中,
∵∠A=60°,∠AEB=90°,
∴∠ABE=30°.
∵AB=4,
∴AE=AB=2,BE2=AB2﹣AE2=12.
又∵BC2=12,
∴BE=BC.
又∵∠CBE=60°,
∴△BEC为等边三角形.
(2)∵△BEC为等边三角形,
∴EC2=BC2=12.
又∵DE2=9,CD2=3,
∴DE2+CD2=12=EC2,
∴△CDE为直角三角形,且∠D=90°,
∴ED⊥CD.
【点睛】本题主要考查了等边三角形的判定与性质、勾股定理和其逆定理,熟练运用勾股定理的逆定理是解题的关键.
22.证明见解析
【分析】根据不同图形拼成的两个正方形面积相等即可证明
【详解】证明:①左图大正方形的边长为:a+b,则面积为(a+b)2,分成了四个直角边为a,b,斜边为c的全等的直角三角形和一个边长为c的小正方形,
;
②右图大正方形的边长为:a+b,则面积为(a+b)2,分成了边长为a的一个正方形,边长为b的一个正方形,还有四个直角边为a,b,斜边为c的全等的直角三角形,
;
综上所述:,即.
【点睛】本题考查利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长的关系进行组合图形.
23.(1)见解析
(2)
(3)的长为
【分析】(1)根据证明三角形全等;
(2)如图2中,延长到,使得,连接.由(1)可知,推出,,利用勾股定理求出,即可解决问题;
(3)如图3中,延长到,使得,连接.证明,设,则,,在中,根据,构建方程即可解决问题.
【详解】(1)证明:如图1中,
在和中,
,
;
(2)解:如图2中,延长到,使得,连接.
由(1)可知,
,,
,
,
;
(3)解:如图3中,延长到,使得,连接.
由(1)可知,,
,,
,
,
,
,
,
设,则,,
在中,,
,
,
.
【点睛】本题属于三角形综合题,考查了全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
24.(1)见解析
(2)
(3)或 21
【分析】(1)由折叠的性质及等腰三角形的判定可得出答案;
(2)利用矩形的性质证得,根据全等三角形的性质得到,设,则由(1)知,, ,在中利用勾股定理即可求解;
(3)当时,设,应分两种情况:第一种情况,点在线段上,如图所示,则,;
第二种情况,点在线段上,如图所示,则,
在中,利用勾股定理即可求解.
【详解】(1)证明:∵四边形ABCD为矩形,
∴ABCD,
∴∠F=∠BAF,
由折叠可知:∠BAF=∠MAF,
∴∠F=∠MAF,
∴AM=MF;
(2)∵点E是边BC的中点,
∴,
∵四边形ABCD为矩形,,
∴ABCD,,
∴∠F=∠BAF,
又∵,
∴,
∴,
设,则由(1)知,,
在中,,
∴,
解得,
∴的长为;
(3)当时,设,应分两种情况:
第一种情况,点在线段上,如图所示,则,
∴在中,,
∴,
解得,
∴的长为;
第二种情况,点在线段的延长线上,如图所示,则,
∴在中,,
∴,解得,
∴的长为
综上可知,当CF=4时,CM的长为或 21
【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,分类讨论的思想是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
