专题1.19用勾股定理解决面积问题 分层练习(含解析)2023-2024学年八年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.19用勾股定理解决面积问题 分层练习(含解析)2023-2024学年八年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览


文档简介
专题1.19 用勾股定理解决面积问题(分层练习)
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习
一、单选题
1.如图,在中,,,,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.13 B.12 C.6 D.3
2.如图,以一个直角三角形的三边为直径作3个半圆,若半圆B、C的面积分别是4、5,则半圆A的面积是( )
A.1 B.3 C. D.9
3.中国是发现和研究勾股定理最古老的国家之一,中国古代称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,其中勾长、股长的平方和等于弦长的平方,即为“勾股定理”,勾股定理是几何学中一颗光彩夺目的明珠,在几何问题中有着广泛的应用.
如图,在直线l上依次摆放着五个正方形.已知斜放置的两个正方形的面积分别是2、3,正放置的三个正方形的面积依次是,则( )
A.4 B.5 C.6 D.7
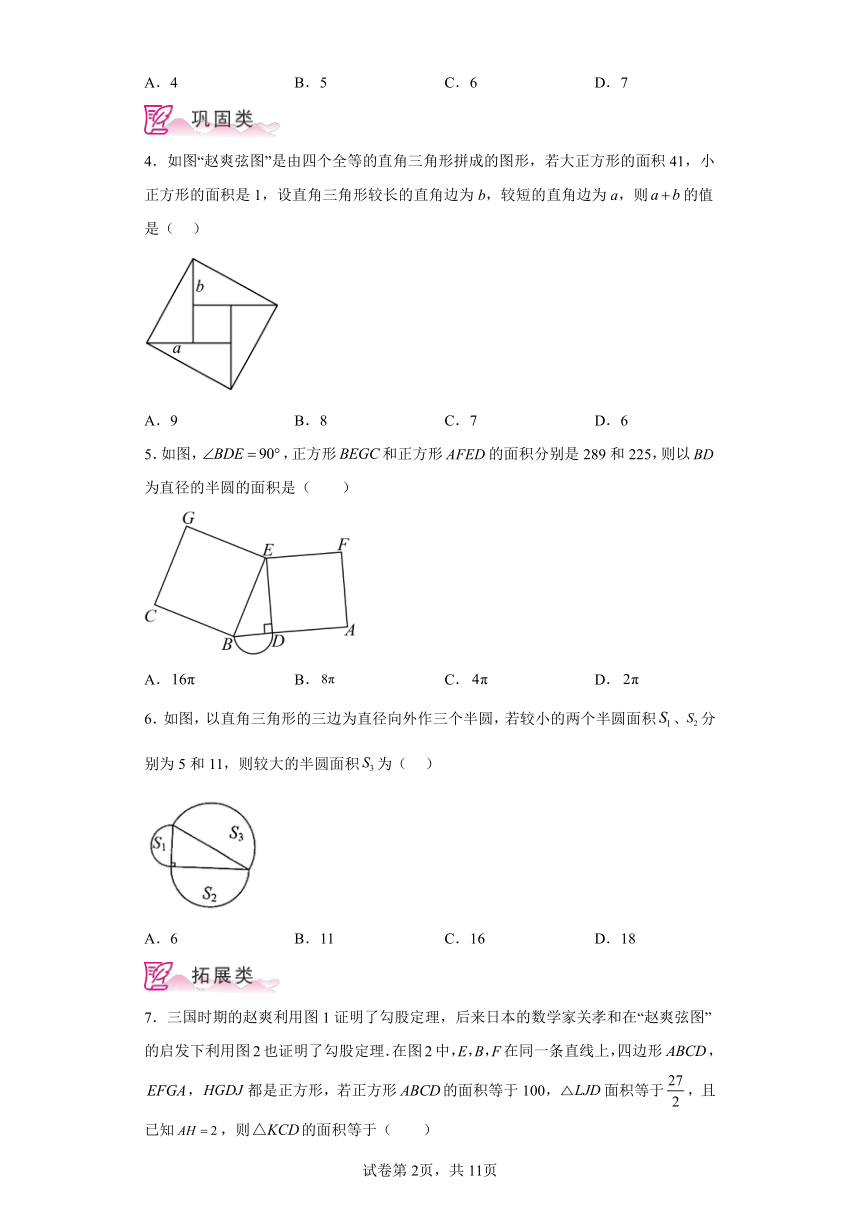
4.如图“赵爽弦图”是由四个全等的直角三角形拼成的图形,若大正方形的面积41,小正方形的面积是1,设直角三角形较长的直角边为b,较短的直角边为a,则的值是( )
A.9 B.8 C.7 D.6
5.如图,,正方形和正方形的面积分别是289和225,则以为直径的半圆的面积是( )
A. B. C. D.
6.如图,以直角三角形的三边为直径向外作三个半圆,若较小的两个半圆面积、分别为5和11,则较大的半圆面积为( )
A.6 B.11 C.16 D.18
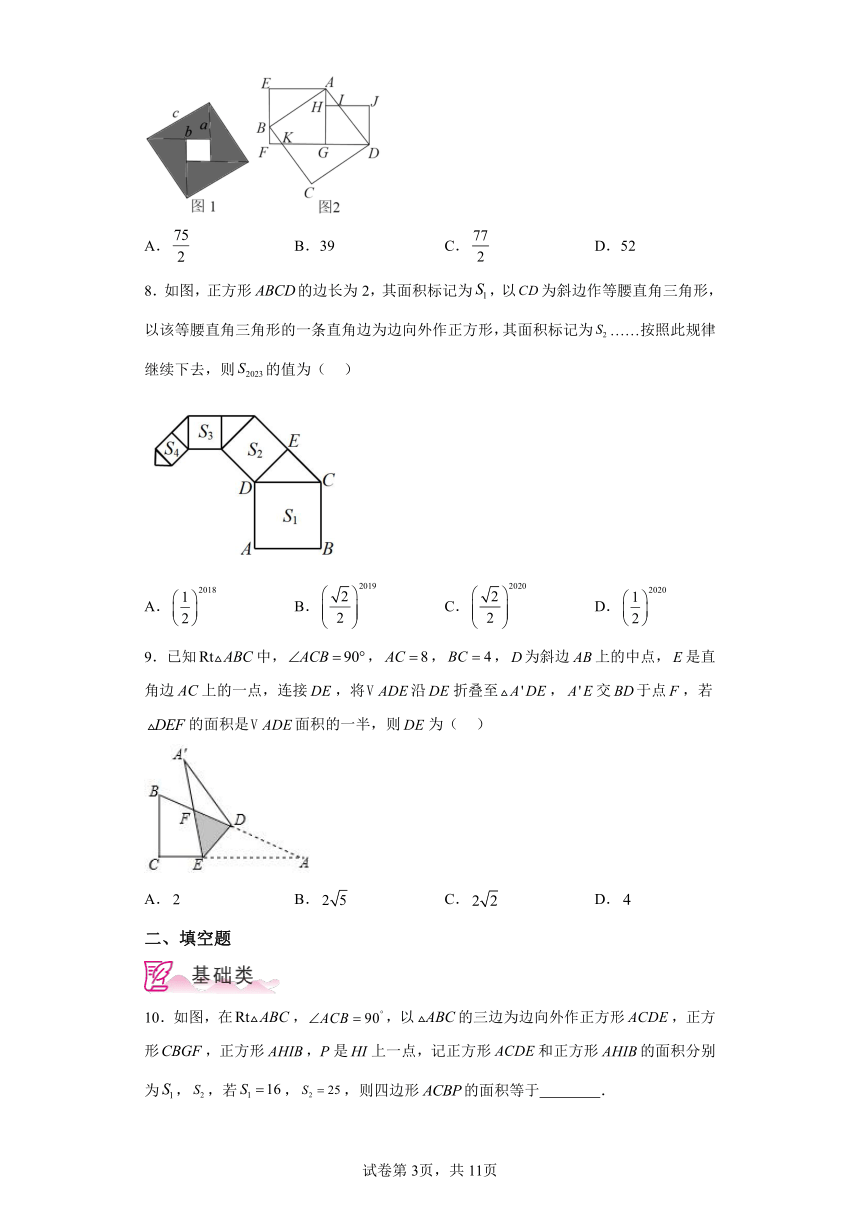
7.三国时期的赵爽利用图1证明了勾股定理,后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中,E,B,F在同一条直线上,四边形,,都是正方形,若正方形的面积等于100,面积等于,且已知,则的面积等于( )
A. B.39 C. D.52
8.如图,正方形的边长为2,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为……按照此规律继续下去,则的值为( )
A. B. C. D.
9.已知中,,,,为斜边上的中点,是直角边上的一点,连接,将沿折叠至,交于点,若的面积是面积的一半,则为( )
A. B. C. D.
二、填空题
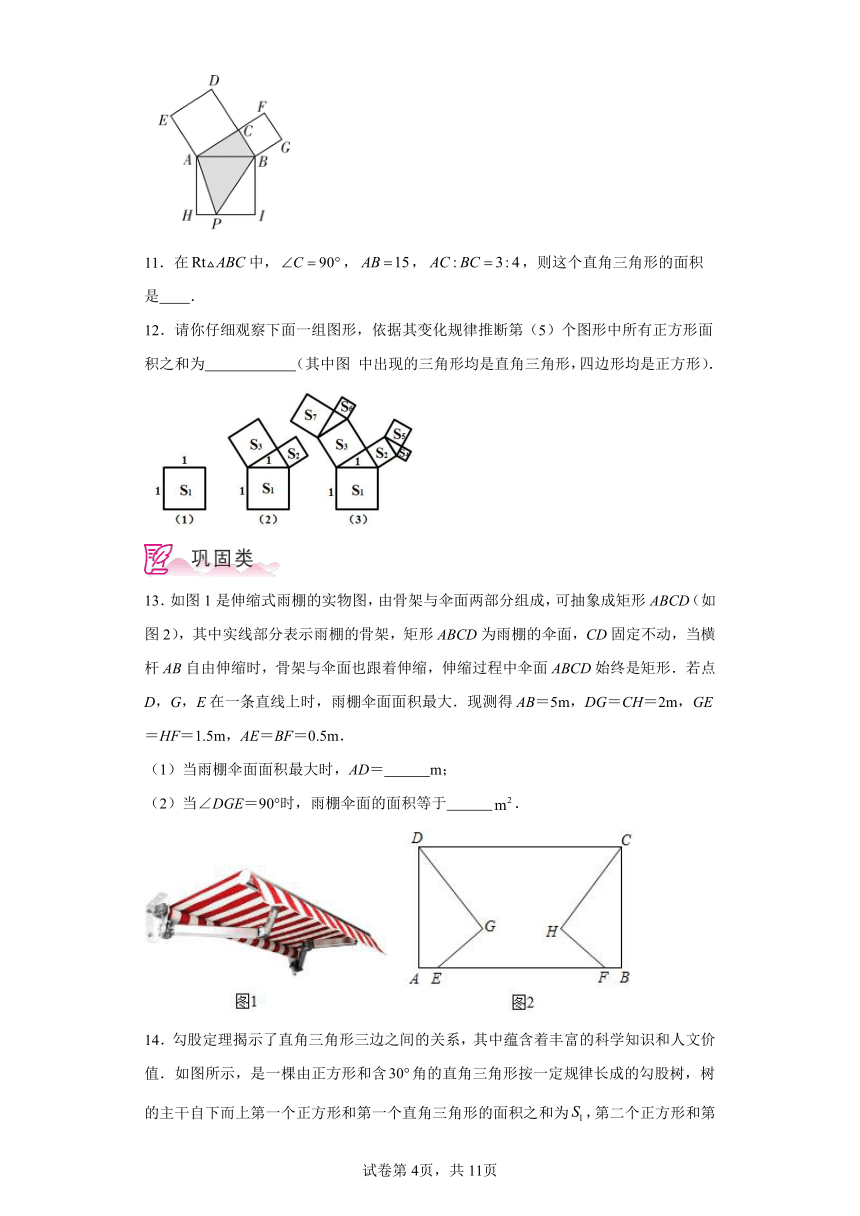
10.如图,在,,以的三边为边向外作正方形,正方形,正方形,P是上一点,记正方形和正方形的面积分别为,,若,,则四边形的面积等于 .
11.在中,,,,则这个直角三角形的面积是 .
12.请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为 (其中图 中出现的三角形均是直角三角形,四边形均是正方形).
13.如图1是伸缩式雨棚的实物图,由骨架与伞面两部分组成,可抽象成矩形ABCD(如图2),其中实线部分表示雨棚的骨架,矩形ABCD为雨棚的伞面,CD固定不动,当横杆AB自由伸缩时,骨架与伞面也跟着伸缩,伸缩过程中伞面ABCD始终是矩形.若点D,G,E在一条直线上时,雨棚伞面面积最大.现测得AB=5m,DG=CH=2m,GE=HF=1.5m,AE=BF=0.5m.
(1)当雨棚伞面面积最大时,AD= m;
(2)当∠DGE=90°时,雨棚伞面的面积等于 .
14.勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为,第二个正方形和第二个直角三角形的面积之和为,…,第个正方形和第个直角三角形的面积之和为.
设第一个正方形的边长为1.
请解答下列问题:
(1) .
(2)通过探究,用含的代数式表示,则 .
15.如图,在中,,点是边上一动点,交于点,当时,的面积恰好等于的面积,连接,则此时=
16.如图,将放在每个小正方形的边长为1的网格中,点均落在格点上.
(1)的面积等于 .
(2)请在如图所示的网格中,用无刻度的直尺,过点画一条直线,交于点,使的面积等于面积的3倍,并简要说明画图的方法 .(不要求证明)
17.如图,图1中是第七届国际数学教育大会(ICME-7)会徽图案、它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的,若代表的面积,代表的面积,以此类推,代表的面则的值为 .
18.如图所示,四边形ADEF为正方形,ABC为等腰直角三角形,D在BC边上,△ABC的面积等于98,BD:DC=2:5,则正方形ADEF的面积等于 .
三、解答题
19.如图,在中,,根据图中所标数据求阴影部分(长方形)的面积.
20.如图,已知在△ABC中,AB=AC=13,D是AB上一点,且CD=12,BD=8.
(1)求△ADC的面积.
(2)求BC的长.
21.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.
(1)如图1所示的大正方形,是由两个正方形和两个形状大小完全相同的长方形拼成的.用两种不同的方法计算图中阴影部分的面积,可以得到的数学等式是 ;
(2)如图2所示的大正方形,是由四个三边长分别为a、b、c的全等的直角三角形(a、b为直角边)和一个正方形拼成,试通过两种不同的方法计算中间正方形的面积,并探究a、b、c之间满足怎样的等量关系.
22.已知中,,,,,是边上的两个动点,其中点从点开始沿方向运动且速度为每秒,点从点开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为秒.
(1)出发2秒后,求的长;
(2)当点在边上运动时,为何值时,的面积是的面积的.
23.我国南宋时期数学家秦九韶,曾经提出用三角形的三边求面积的秦九韶公式.他的方法大致如下:如图,给定一个三角形,三边分别为,,,过点作于,为,的公共边,则可以利用这个等量关系,运用勾股定理建立方程,求出,再求出高,从而求出三角形的面积.
请你用这一方法,解决下列问题:
已知,,,,求的面积.
24.阅读材料:如图1,如果直角三角形两直角边长分别为a,b,斜边长为c,那么.即直角三角形两直角边的平方和等于斜边的平方.
(1)若直角三角形两直角边长分别为3和4,则斜边长为 ;
(2)如图2,中,,设AC长为x,BC长为y,,中,,.
①请用含有x,y的代数式表示的面积 ;
②四边形CADB的面积是否为定值,若是,请求出这个定值;若不是,请说明理由.
25.用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理.
(2)如图2,在中,是边上的高,,求的长度;
(3)如图1,若大正方形的面积是13,小正方形的面积是1,求的值.
26.在△ABC中,已知三角形的三边长,求这个三角形的面积.
(1)如图1,已知AC=5,BC=12,AB=13,则△ABC的面积是______;
(2)如图2,已知BC=10,AB=AC=13,求△ABC的面积;
(3)如图3,已知AC=8,BC=10,AB=12,求△ABC的面积.
27.如图是由边长为1的小正方形组成的正方形网格,的顶点都在格点(正方形的顶点)上.
(1)的面积是____;
(2)的形状是______;
(3)若的面积与的面积相等,则网格中满足条件的格点D(不与C重合)共有______个.
28.(1)如图1,点在的边上,,,,,求的面积;
(2)如图2,中,,,,求的面积.
(3)如图3,在中,,,,求的面积.
29.如图,CE⊥AB于点E,BD⊥AC于点D,AB=AC.
(1)求证:△ABD≌△ACE.
(2)连接BC,若AD=6,CD=4,求△ABC的面积.
30.在直线l上摆放着三个正方形
(1)如图1,已知水平放置的两个正方形的边长依次是a,b斜着放置的正方形的面积S= ,两个直角三角形的面积和为 ;(均用a,b表示)
(2)如图2,小正方形面积S1=1,斜着放置的正方形的面积S=4,求图中两个钝角三角形的面积m1和m2,并给出图中四个三角形的面积关系;
(3)图3是由五个正方形所搭成的平面图,T与S分别表示所在的三角形与正方形的面积,试写出T与S的关系式,并利用(1)和(2)的结论说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.A
【分析】由勾股定理求出AB2,再由正方形的面积公式即可得到答案.
【详解】解:在△ABC中,∠C=90°,AC=3,BC=2,
∴AB2=AC2+BC2=32+22=13,
∴正方形的面积=AB2=13,
故选:A.
【点睛】本题考查了勾股定理、正方形的面积计算等知识,熟练掌握勾股定理是解题的关键.
2.A
【分析】根据半圆的面积计算公式即可计算S与直径的关系,根据直角三角形中勾股定理的应用可以计算直角△ABC中三边关系,根据这两个关系式即可解题.
【详解】解:如图,半圆B、C、A的面积分用S2、S1、S3表示;
S1=π,
S2=π,
S3=π,
∵在直角△ABC中,AB2=AC2+BC2,
∴S2+S3=S1,
半圆A的面积是5-4=1;
故选:A.
【点睛】本题考查了勾股定理在直角三角形中的灵活运用,考查了半圆的面积计算公式,本题中正确的根据勾股定理求出AB,AC,BC的关系是解题的关键.
3.B
【分析】结合正方形的性质证明△ABC≌△BDE,根据全等三角形的性质推出,同理,,据此求解即可.
【详解】解:如图,
∵图中的四边形均为正方形,
∴,,,
∴∠ABC+∠DBE=90°,∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵,
∴,
∵,
∴,
同理,,
∴,
故选:B.
【点睛】此题考查了全等三角形的判定与性质,结合正方形的性质证明△ABC≌△BDE是解题的关键.
4.A
【分析】先求出小三角形的面积,然后根据勾股定理分析即可.
【详解】解:因为大正方形的面积是41,小正方形的面积是1,
所以一个小三角形的面积是,三角形的斜边为,
所以,,
所以,
所以(负值已舍).
故选:A.
【点睛】本题考查了勾股定理,熟练掌握勾股定理的相关知识是解题的关键.
5.B
【分析】利用勾股定理求出,再求半圆的面积即可.
【详解】解:∵正方形和正方形的面积分别是289和225,
∴,
∵,
∴,
∴以为直径的半圆的面积为:;
故选B.
【点睛】本题考查勾股定理.熟练掌握勾股定理,是解题的关键.
6.C
【分析】利用直角三角形的边长就可以表示出、、的大小,三角形的边满足勾股定理,即可得出、、的等量关系,代值可求解.
【详解】设直角三角形的两直角边为a、b,斜边为c,则
∵
∴,
∴
∵,
∴
∴C选项正确.
故选:C
【点睛】本题考查了勾股定理,关键是对勾股定理进行的证明,难度程度适中.
7.A
【分析】设,则,由勾股定理得出,解得,则,由勾股定理求出,证明,由全等三角形的性质得出,则可得出答案.
【详解】解:∵四边形和四边形是正方形,正方形的面积等于100,
∴,,
设,则,
∵,
∴,
解得舍去,
∴,
∵面积等于,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴的面积.
故选:A.
【点睛】本题考查了全等三角形的判定与性质,勾股定理,正方形的性质,熟练掌握勾股定理是解题的关键.
8.D
【分析】根据等腰直角三角形的性质可得出,根据数的变化找出变化规律“”,依此规律即可得出结论.
【详解】∵正方形的边长为,为等腰直角三角形,
∴,,
∴.
观察,发现规律:,,,,,
∴,
当时,,
故选:D.
【点睛】本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解决该题型题目时,写出部分Sn的值,根据数值的变化找出变化规律 “”是关键.
9.C
【分析】连接BE,过D作DG⊥AC于G,先判定(SAS),即可得出,再根据勾股定理求得CE的长,进而得出EG和DG的长,再根据勾股定理即可得到DE的长.
【详解】解:如图所示,连接,过作于,
∵,,,
∴由勾股定理得,
由折叠可得,与全等,
∵的面积是面积的一半,
∴的面积是面积的一半,且,
∴是的中点,
又∵是的中点,
∴,即是的中点,
又∵,
∴≌,
∴,
又∵,
∴中,,
∵,是的中点,
∴是的中点,即,
∴,,
∴中,,
故选:.
【点睛】本题主要考查了折叠问题以及勾股定理的运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
10.18.5
【分析】先求出的边长,再利用进四边形的面积解题即可得到答案.
【详解】正方形和正方形的面积分别为,,且,,
正方形的面积
,
四边形的面积
故答案为:.
【点睛】本题考查了勾股定理,正确掌握勾股定理是解题的关键.
11.54
【分析】先根据已知比例式设,则,再利用勾股定理求出的值,然后利用直角三角形的面积公式即可得.
【详解】设,则
由勾股定理得,即
解得
则的面积为
故答案为:54.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题关键.
12.5
【分析】根据勾股定理,第(2)个图形中两个小正方形的面积和等于第一个正方形的面积,图形(2)中所有正方形的积和等于2;依此类推,可发现第(n)个图形中所有正方形的面积和等于第一个正方形的面积的n倍,进而得问题答案.
【详解】解:设第(2)个图形中直角三角形的是三条边分别是a,b,c,
根据勾股定理,得a2+b2=c2,
即S2+S3=S1=1;
∴第(2)个图形中所有正方形的面积之和为S1+S2+S3=2,
同理可得:第(3)个图形中所有正方形的面积之和为3,
可得规律:第(n)个图形中所有正方形的面积之和为n,
∴第(5)个图形中所有正方形的面积之和为5,
故答案为:5.
【点睛】此题考查了正方形的性质,以及勾股定理,其中能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系是解本题的关键.
13.
【分析】(1)当D,G,E在一条直线上时,雨棚伞面面积最大,根据勾股定理可以得到AD的长;
(2)根据勾股定理可以得到DE的长,然后再根据∠DAE=90°,AE=0.5m,即可求得AD的长,然后即可计算出当∠DGE=90°时,雨棚伞面的面积.
【详解】解:当D,G,E在一条直线上时,雨棚伞面面积最大,
此时AD=(m).
故答案为:2;
(2)连接DE,如图2所示,
∵DG=2m,GE=1.5m,∠DGE=90°,
∴DE==2.5(m),
∵∠DAE=90°,AE=0.5m,
∴AD=(m),
∵AB=5m,
∴雨棚伞面的面积是:AB AD=5×=5(m2),
故答案为:5.
【点睛】本题考查了勾股定理的应用,解答本题的关键是明确题意,求出矩形的宽.
14. (为整数)
【分析】根据正方形的面积公式求出面积,再根据直角三角形三条边的关系运用勾股定理求出三角形的直角边,求出S1,然后利用正方形与三角形面积扩大与缩小的规律推导出公式.
【详解】解:(1)∵第一个正方形的边长为1,
∴正方形的面积为1,
又∵直角三角形一个角为30°,
∴三角形的一条直角边为,另一条直角边就是,
∴三角形的面积为,
∴S1=;
(2)∵第二个正方形的边长为,它的面积就是,也就是第一个正方形面积的,
同理,第二个三角形的面积也是第一个三角形的面积的,
∴S2=() ,
依此类推,S3=() ,
即S3=() ,
Sn=(n为整数).
故答案为:(1) ;(2)(为整数)
【点睛】本题考查勾股定理的运用,正方形的性质以及含30°角的直角三角形的性质.能够发现每一次得到的新的正方形和直角三角形的面积与原正方形和直角三角形的面积之间的关系是解题的关键.
15.
【分析】延长,过点作的垂线,垂足为点,根据和的面积相等可知线段AD是中线,,根据直角三角形的勾股定理可得的长度.
【详解】解:延长,过点作的垂线,垂足为点,如图所示
∵和的面积相等
∴
∵
∴
∵根据三角形中线的性质可知
∴
∵
∴
∴在中可得
在中可得
∴
∴在中可得
故答案为:
【点睛】本题考查了三角形的中线和面积的关系以及勾股定理等知识点,灵活运用三角形的中线和面积的关系是解题的关键.
16. 2 见解析
【分析】(1)根据三角形的面积公式,即可求出答案;
(2)根据题意,在BC上取BD=3CD,即可画出图形.
【详解】解:(1);
(2)如图:找BC的四等分点,连接AD为所求.
作法:①取线段,在线段取一点,使.
②过所作的平行线,使,交于点.
③作直线
则直线就是所求作的直线.
【点睛】本题考查了复杂作图,以及三角形的面积,解题的关键是学会利用分割法求三角形面积,巧妙利用格点作四等分点,属于作图中比较难的题目.
17.7
【分析】根据勾股定理求得,进而求得,再求得,即可求解.
【详解】解:,
,
……
,
,
……
,
.
故答案为:.
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
18.116
【分析】过点A作,交BC于点H,根据等腰直角三角形的性质可得:,利用三角形面积公式可得:,然后根据勾股定理得出:,根据题意BD:DC=2:5,结合,可得,,在中,利用勾股定理可得正方形的边长,根据正方形面积公式即可求出面积.
【详解】解:过点A作,交BC于点H,
∴,
∵等腰直角的面积等于98,
∴,
∴,
又∵BD:DC=2:5,
∴,,
在中,
,
∴正方形ABCD的面积:.
故本题答案为:116.
【点睛】题目主要考查等腰直角三角形的性质、线段比及勾股定理,作出辅助线应用勾股定理是解题关键.
19.
【分析】先利用勾股定理计算的长,再利用长方形的面积公式进行计算即可.
【详解】解:∵,
∴.
∴阴影部分的面积为.
【点睛】本题考查的是勾股定理的应用,熟记勾股定理并灵活运用是解本题的关键.
20.(1)30;(2)4.
【分析】(1)根据勾股定理的逆定理得到∠ADC=90°,根据三角形的面积公式计算即可;
(2)根据勾股定理计算,得到答案.
【详解】解:(1)∵AB=13,BD=8,
∴AD=AB﹣BD=5,
∴AC=13,CD=12,
∴AD2+CD2=AC2,
∴∠ADC=90°,即△ADC是直角三角形,
∴△ADC的面积=×AD×CD=×5×12=30;
(2)在Rt△BDC中,∠BDC=180°﹣90°=90°,
由勾股定理得:BC==4,即BC的长是4.
【点睛】此题主要考查勾股定理的应用,解题的关键是熟知直角三角形的性质及勾股定理的应用.
21.(1)a2+b2= ( a+b) 2-2ab;
(2).
【分析】(1)分别用两种不同的方法表示阴影部分面积即可得等式.
(2)先直接用c表示中间正方形的面积,再用大正方形的面积减去4个小三角形的面积表示中间正方形的面积,从而可得结论.
【详解】(1)解∶如图1,∵ S阴影=a2+b2,S阴影= ( a+b) 2-2ab .
∴a2+b2= ( a+b) 2-2ab,
故答案为∶a2+b2= ( a+b) 2-2ab;
(2)解:如图2,∵S中间正方形=c2,S中间正方形=(a+b)2-4×ab,
∴,
∴.
【点睛】本题考查完全平方公式及勾股定理的几何背景,用两种方法表示同一个图形的面积是求解本题的关键.
22.(1)
(2)
【分析】(1)求出,利用勾股定理求出的长;
(2)先求出,根据的面积是面积的得,计算即可;
【详解】(1)解:当出发2秒后,,
∴,
∵,
∴
(2)解:∵,
∴,
∴,
得.
【点睛】此题考查了勾股定理,三角形与动点问题,实际问题与一元一次方程,列比例求解,解题中运用分类思想,正确掌握勾股定理的计算公式是解题的关键.
23.的面积为84
【分析】根据题意和题目中的数据,利用勾股定理可以列出相应的方程,然后求出BD的长,再求出AD的长,即可计算出△ABC的面积.
【详解】设BD的长为x,则CD的长为14 - x,
∵AD⊥BC,
∴∠ADB=∠ADC=90°
∴AD2= AB2- BD2
AD2= AC2- CD2.
∴AB2- BD2 = AC2- CD2,
∵AB= 13, AC= 15,
∴132-x2=152-(14- x)2,
解得x = 5,
∴BD=5,CD=14-x=9,
∴AD2= 132- 52,
解得AD= 12,
∴S△ABC =
即△A BC的面积是84.
【点睛】本题考查勾股定理的应用,解答本题的关键是求出BD和AD的长.
24.(1)5
(2)①;②四边形CADB的面积为定值,为16
【分析】(1)直接根据勾股定理,即可求解;
(2)①根据勾股定理可得,,可得,再由,即可求解;②根据,即可求解.
【详解】(1)解:根据勾股定理,得:斜边长为;
故答案为:5
(2)解:①∵ ,
∴,
∵∠D=90°,
∴,
∵AD=BD,
∴,
∴,
∴;
故答案为:
②四边形CADB的面积为为定值,理由如下:
=16
【点睛】本题主要考查了勾股定理的应用,完全平方公式的应用,明确题意,理解勾股定理是解题的关键.
25.(1)见解析
(2)
(3)25
【分析】(1)如图1所示,大正方形的面积等于四个全等的直角三角形面积与小正方形面积和,用代数式表示出各部分面积按要求列等式化简即可得证;
(2)利用勾股定理得到,根据等面积法列式求解即可得到;
(3)由(1)的结论,结合完全平方公式变形,代值求解即可得到答案.
【详解】(1)解:如图1所示:
大正方形的面积等于四个全等的直角三角形面积与小正方形面积和,
;;;
,即;
(2)解:如图2所示:
在中,,,
∴由勾股定理可得,
是边上的高,
由等面积法可得,
,,
∴;
(3)解:∵大正方形的面积是13,小正方形的面积是1,,如图1所示:
∴,
∴,
由(1)知,
∴,
∴,即的值为25.
【点睛】本题考查等面积法解决问题,涉及勾股定理证明、等面积法求线段长、以及完全平方公式与勾股定理综合,熟练掌握等面积法求解是解决问题的关键.
26.(1)30
(2)60
(3)15
【分析】(1)根据勾股定理的逆定理判断△ABC是直角三角形,再求面积即可;
(2)作AD⊥BC于D,由等腰三角形三线合一的性质及勾股定理求出AD的长度,再根据面积公式计算即可;
(3)作CD⊥AB于D,先由勾股定理计算出CD的长度,再根据面积公式计算即可.
【详解】(1)∵AC=5,BC=12,AB=13,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°,
∴△ABC的面积=AC×BC=×5×12=30;
故答案为:30;
(2)作AD⊥BC于D,如图2所示:
∵AB=AC,
∴BD=CD=BC=5,
∴AD===12,
∴△ABC的面积=BC×AD=×10×12=60;
(3)作CD⊥AB于D,如图3所示:
由勾股定理得:CD2=AC2﹣AD2=BC2﹣BD2,即82﹣AD2=102﹣(12﹣AD)2,
解得:AD=,
∴CD==,
∴△ABC的面积=AB×CD=×12×=15.
【点睛】本题考查了勾股定理及其逆定理、等腰三角形的性质,熟练掌握知识点是解题的关键.
27.(1)
(2)等腰直角三角形
(3)2
【分析】(1)利用矩形和三角形的面积公式即可得到结论;
(2)利用网格计算,,长度进行判断三角形的形状;
(3)利用同底等高的三角形的面积相等解题即可.
【详解】(1)解:
故答案为:.
(2)解:∵,,
∴,
∴是等腰直角三角形
故答案为:等腰直角三角形.
(3)过点C作,则平行线上的点与A、B形成的三角形面积都等于的面积,即网格中满足条件的格点D共有个,
故答案为:.
【点睛】本题考查三角形的面积,三角形的形状,应用数形结合的思想解决问题是解题的关键.
28.(1)150;(2)66;(3)84
【分析】(1)根据勾股定理求出,求出,根据勾股定理的逆定理得出△ADB是直角三角形,根据勾股定理求出CD,求出BC,再求出△ABC的面积即可;
(2)过E作EM⊥FG,交GF的延长线于M,设FM=x,则GM=11+x,根据勾股定理得出,代入求出x,再求出EM,最后求出△EFG的面积即可;
(3)过点E作EH⊥FG于点H,由勾股定理可得,从而可得,设FH=x,则GH=14-x,即,再求出EH,即可求解.
【详解】解:(1),,,
,,
,
是直角三角形,
即,
,
由勾股定理得:,
,
的面积;
(2)过作,交的延长线于,设,则,
在和中,由勾股定理得:,,
,
,
解得:,
即,
,
的面积.
(3)解:如图,过点作于点,
在和中,由勾股定理可得:
,,
,
设,则,
,,,
,
解得:,
,
,
的面积为84
【点睛】本题考查了勾股定理,勾股定理的逆定理和三角形的面积等知识点,能熟记勾股定理的逆定理是解此题的关键,注意:如果一个三角形的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形.
29.(1)见解析
(2)
【分析】(1)根据题目所给条件证即可;
(2)由可得,由勾股定理可求BD,即可求解;
【详解】(1)证明:∵,
∴,
∵,
∴.
(2)解:∵,
∴,
在中,,
∴.
【点睛】本题主要考查三角形的全等证明、勾股定理,掌握三角形的全等证明及性质是解题的关键.
30.(1)a2+b2,ab;(2)四个三角形的面积相等;(3)S=T.
【分析】(1)根据题意,可以证得中间的两个三角形全等,再根据勾股定理,即可得出答案;
(2)求出两个钝角三角形的底边和高,然后根据三角形的面积公式求解即可;
(3)利用勾股定理分别求出S和T的值,然后比较求解即可.
【详解】(1)如图1所示:∵三个四边形均为正方形,
∴∠ACB+∠BAC=90°,∠ACB+∠DCE=90°,AC=CE,
∴∠BAC=∠DCE,
∵∠ABC=∠CDE=90°,
∴△ABC≌△CDE,
∴BC=DE=b,AB=CD=a,
∴S△ABC+S△CDE=ab,
同时AC2=AB2+BC2,
∵两个正方形的面积分别为a2,b2,
∴S=a2+b2,
(2)如图2所示,a=1,斜正方形边长c=2,b=,
由30°角和60°角易求出面积为m1的三角形底边长为1,高为,故m1=;
面积为m2的三角形边长为,高为1,故m2=.
结论:四个三角形的面积相等.
(3)S=T.如图3所示,首先由(2)知:T=S△ABC,
设小正方形边长为a,大正方形边长为b,
由(1)知:S=a2+b2,又图中四个小三角形的面积m=ab,
S△ABC=a2+b2+(a2+b2)+4×ab﹣(a+b)(2a+2b)=a2+b2=S,
∴S=T.
【点睛】本题考查了勾股定理的运用,结合正方形的面积求解公式求解.
答案第1页,共2页
答案第1页,共2页
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习
一、单选题
1.如图,在中,,,,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.13 B.12 C.6 D.3
2.如图,以一个直角三角形的三边为直径作3个半圆,若半圆B、C的面积分别是4、5,则半圆A的面积是( )
A.1 B.3 C. D.9
3.中国是发现和研究勾股定理最古老的国家之一,中国古代称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,其中勾长、股长的平方和等于弦长的平方,即为“勾股定理”,勾股定理是几何学中一颗光彩夺目的明珠,在几何问题中有着广泛的应用.
如图,在直线l上依次摆放着五个正方形.已知斜放置的两个正方形的面积分别是2、3,正放置的三个正方形的面积依次是,则( )
A.4 B.5 C.6 D.7
4.如图“赵爽弦图”是由四个全等的直角三角形拼成的图形,若大正方形的面积41,小正方形的面积是1,设直角三角形较长的直角边为b,较短的直角边为a,则的值是( )
A.9 B.8 C.7 D.6
5.如图,,正方形和正方形的面积分别是289和225,则以为直径的半圆的面积是( )
A. B. C. D.
6.如图,以直角三角形的三边为直径向外作三个半圆,若较小的两个半圆面积、分别为5和11,则较大的半圆面积为( )
A.6 B.11 C.16 D.18
7.三国时期的赵爽利用图1证明了勾股定理,后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中,E,B,F在同一条直线上,四边形,,都是正方形,若正方形的面积等于100,面积等于,且已知,则的面积等于( )
A. B.39 C. D.52
8.如图,正方形的边长为2,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为……按照此规律继续下去,则的值为( )
A. B. C. D.
9.已知中,,,,为斜边上的中点,是直角边上的一点,连接,将沿折叠至,交于点,若的面积是面积的一半,则为( )
A. B. C. D.
二、填空题
10.如图,在,,以的三边为边向外作正方形,正方形,正方形,P是上一点,记正方形和正方形的面积分别为,,若,,则四边形的面积等于 .
11.在中,,,,则这个直角三角形的面积是 .
12.请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为 (其中图 中出现的三角形均是直角三角形,四边形均是正方形).
13.如图1是伸缩式雨棚的实物图,由骨架与伞面两部分组成,可抽象成矩形ABCD(如图2),其中实线部分表示雨棚的骨架,矩形ABCD为雨棚的伞面,CD固定不动,当横杆AB自由伸缩时,骨架与伞面也跟着伸缩,伸缩过程中伞面ABCD始终是矩形.若点D,G,E在一条直线上时,雨棚伞面面积最大.现测得AB=5m,DG=CH=2m,GE=HF=1.5m,AE=BF=0.5m.
(1)当雨棚伞面面积最大时,AD= m;
(2)当∠DGE=90°时,雨棚伞面的面积等于 .
14.勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为,第二个正方形和第二个直角三角形的面积之和为,…,第个正方形和第个直角三角形的面积之和为.
设第一个正方形的边长为1.
请解答下列问题:
(1) .
(2)通过探究,用含的代数式表示,则 .
15.如图,在中,,点是边上一动点,交于点,当时,的面积恰好等于的面积,连接,则此时=
16.如图,将放在每个小正方形的边长为1的网格中,点均落在格点上.
(1)的面积等于 .
(2)请在如图所示的网格中,用无刻度的直尺,过点画一条直线,交于点,使的面积等于面积的3倍,并简要说明画图的方法 .(不要求证明)
17.如图,图1中是第七届国际数学教育大会(ICME-7)会徽图案、它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的,若代表的面积,代表的面积,以此类推,代表的面则的值为 .
18.如图所示,四边形ADEF为正方形,ABC为等腰直角三角形,D在BC边上,△ABC的面积等于98,BD:DC=2:5,则正方形ADEF的面积等于 .
三、解答题
19.如图,在中,,根据图中所标数据求阴影部分(长方形)的面积.
20.如图,已知在△ABC中,AB=AC=13,D是AB上一点,且CD=12,BD=8.
(1)求△ADC的面积.
(2)求BC的长.
21.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.
(1)如图1所示的大正方形,是由两个正方形和两个形状大小完全相同的长方形拼成的.用两种不同的方法计算图中阴影部分的面积,可以得到的数学等式是 ;
(2)如图2所示的大正方形,是由四个三边长分别为a、b、c的全等的直角三角形(a、b为直角边)和一个正方形拼成,试通过两种不同的方法计算中间正方形的面积,并探究a、b、c之间满足怎样的等量关系.
22.已知中,,,,,是边上的两个动点,其中点从点开始沿方向运动且速度为每秒,点从点开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为秒.
(1)出发2秒后,求的长;
(2)当点在边上运动时,为何值时,的面积是的面积的.
23.我国南宋时期数学家秦九韶,曾经提出用三角形的三边求面积的秦九韶公式.他的方法大致如下:如图,给定一个三角形,三边分别为,,,过点作于,为,的公共边,则可以利用这个等量关系,运用勾股定理建立方程,求出,再求出高,从而求出三角形的面积.
请你用这一方法,解决下列问题:
已知,,,,求的面积.
24.阅读材料:如图1,如果直角三角形两直角边长分别为a,b,斜边长为c,那么.即直角三角形两直角边的平方和等于斜边的平方.
(1)若直角三角形两直角边长分别为3和4,则斜边长为 ;
(2)如图2,中,,设AC长为x,BC长为y,,中,,.
①请用含有x,y的代数式表示的面积 ;
②四边形CADB的面积是否为定值,若是,请求出这个定值;若不是,请说明理由.
25.用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理.
(2)如图2,在中,是边上的高,,求的长度;
(3)如图1,若大正方形的面积是13,小正方形的面积是1,求的值.
26.在△ABC中,已知三角形的三边长,求这个三角形的面积.
(1)如图1,已知AC=5,BC=12,AB=13,则△ABC的面积是______;
(2)如图2,已知BC=10,AB=AC=13,求△ABC的面积;
(3)如图3,已知AC=8,BC=10,AB=12,求△ABC的面积.
27.如图是由边长为1的小正方形组成的正方形网格,的顶点都在格点(正方形的顶点)上.
(1)的面积是____;
(2)的形状是______;
(3)若的面积与的面积相等,则网格中满足条件的格点D(不与C重合)共有______个.
28.(1)如图1,点在的边上,,,,,求的面积;
(2)如图2,中,,,,求的面积.
(3)如图3,在中,,,,求的面积.
29.如图,CE⊥AB于点E,BD⊥AC于点D,AB=AC.
(1)求证:△ABD≌△ACE.
(2)连接BC,若AD=6,CD=4,求△ABC的面积.
30.在直线l上摆放着三个正方形
(1)如图1,已知水平放置的两个正方形的边长依次是a,b斜着放置的正方形的面积S= ,两个直角三角形的面积和为 ;(均用a,b表示)
(2)如图2,小正方形面积S1=1,斜着放置的正方形的面积S=4,求图中两个钝角三角形的面积m1和m2,并给出图中四个三角形的面积关系;
(3)图3是由五个正方形所搭成的平面图,T与S分别表示所在的三角形与正方形的面积,试写出T与S的关系式,并利用(1)和(2)的结论说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.A
【分析】由勾股定理求出AB2,再由正方形的面积公式即可得到答案.
【详解】解:在△ABC中,∠C=90°,AC=3,BC=2,
∴AB2=AC2+BC2=32+22=13,
∴正方形的面积=AB2=13,
故选:A.
【点睛】本题考查了勾股定理、正方形的面积计算等知识,熟练掌握勾股定理是解题的关键.
2.A
【分析】根据半圆的面积计算公式即可计算S与直径的关系,根据直角三角形中勾股定理的应用可以计算直角△ABC中三边关系,根据这两个关系式即可解题.
【详解】解:如图,半圆B、C、A的面积分用S2、S1、S3表示;
S1=π,
S2=π,
S3=π,
∵在直角△ABC中,AB2=AC2+BC2,
∴S2+S3=S1,
半圆A的面积是5-4=1;
故选:A.
【点睛】本题考查了勾股定理在直角三角形中的灵活运用,考查了半圆的面积计算公式,本题中正确的根据勾股定理求出AB,AC,BC的关系是解题的关键.
3.B
【分析】结合正方形的性质证明△ABC≌△BDE,根据全等三角形的性质推出,同理,,据此求解即可.
【详解】解:如图,
∵图中的四边形均为正方形,
∴,,,
∴∠ABC+∠DBE=90°,∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵,
∴,
∵,
∴,
同理,,
∴,
故选:B.
【点睛】此题考查了全等三角形的判定与性质,结合正方形的性质证明△ABC≌△BDE是解题的关键.
4.A
【分析】先求出小三角形的面积,然后根据勾股定理分析即可.
【详解】解:因为大正方形的面积是41,小正方形的面积是1,
所以一个小三角形的面积是,三角形的斜边为,
所以,,
所以,
所以(负值已舍).
故选:A.
【点睛】本题考查了勾股定理,熟练掌握勾股定理的相关知识是解题的关键.
5.B
【分析】利用勾股定理求出,再求半圆的面积即可.
【详解】解:∵正方形和正方形的面积分别是289和225,
∴,
∵,
∴,
∴以为直径的半圆的面积为:;
故选B.
【点睛】本题考查勾股定理.熟练掌握勾股定理,是解题的关键.
6.C
【分析】利用直角三角形的边长就可以表示出、、的大小,三角形的边满足勾股定理,即可得出、、的等量关系,代值可求解.
【详解】设直角三角形的两直角边为a、b,斜边为c,则
∵
∴,
∴
∵,
∴
∴C选项正确.
故选:C
【点睛】本题考查了勾股定理,关键是对勾股定理进行的证明,难度程度适中.
7.A
【分析】设,则,由勾股定理得出,解得,则,由勾股定理求出,证明,由全等三角形的性质得出,则可得出答案.
【详解】解:∵四边形和四边形是正方形,正方形的面积等于100,
∴,,
设,则,
∵,
∴,
解得舍去,
∴,
∵面积等于,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴的面积.
故选:A.
【点睛】本题考查了全等三角形的判定与性质,勾股定理,正方形的性质,熟练掌握勾股定理是解题的关键.
8.D
【分析】根据等腰直角三角形的性质可得出,根据数的变化找出变化规律“”,依此规律即可得出结论.
【详解】∵正方形的边长为,为等腰直角三角形,
∴,,
∴.
观察,发现规律:,,,,,
∴,
当时,,
故选:D.
【点睛】本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解决该题型题目时,写出部分Sn的值,根据数值的变化找出变化规律 “”是关键.
9.C
【分析】连接BE,过D作DG⊥AC于G,先判定(SAS),即可得出,再根据勾股定理求得CE的长,进而得出EG和DG的长,再根据勾股定理即可得到DE的长.
【详解】解:如图所示,连接,过作于,
∵,,,
∴由勾股定理得,
由折叠可得,与全等,
∵的面积是面积的一半,
∴的面积是面积的一半,且,
∴是的中点,
又∵是的中点,
∴,即是的中点,
又∵,
∴≌,
∴,
又∵,
∴中,,
∵,是的中点,
∴是的中点,即,
∴,,
∴中,,
故选:.
【点睛】本题主要考查了折叠问题以及勾股定理的运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
10.18.5
【分析】先求出的边长,再利用进四边形的面积解题即可得到答案.
【详解】正方形和正方形的面积分别为,,且,,
正方形的面积
,
四边形的面积
故答案为:.
【点睛】本题考查了勾股定理,正确掌握勾股定理是解题的关键.
11.54
【分析】先根据已知比例式设,则,再利用勾股定理求出的值,然后利用直角三角形的面积公式即可得.
【详解】设,则
由勾股定理得,即
解得
则的面积为
故答案为:54.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题关键.
12.5
【分析】根据勾股定理,第(2)个图形中两个小正方形的面积和等于第一个正方形的面积,图形(2)中所有正方形的积和等于2;依此类推,可发现第(n)个图形中所有正方形的面积和等于第一个正方形的面积的n倍,进而得问题答案.
【详解】解:设第(2)个图形中直角三角形的是三条边分别是a,b,c,
根据勾股定理,得a2+b2=c2,
即S2+S3=S1=1;
∴第(2)个图形中所有正方形的面积之和为S1+S2+S3=2,
同理可得:第(3)个图形中所有正方形的面积之和为3,
可得规律:第(n)个图形中所有正方形的面积之和为n,
∴第(5)个图形中所有正方形的面积之和为5,
故答案为:5.
【点睛】此题考查了正方形的性质,以及勾股定理,其中能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系是解本题的关键.
13.
【分析】(1)当D,G,E在一条直线上时,雨棚伞面面积最大,根据勾股定理可以得到AD的长;
(2)根据勾股定理可以得到DE的长,然后再根据∠DAE=90°,AE=0.5m,即可求得AD的长,然后即可计算出当∠DGE=90°时,雨棚伞面的面积.
【详解】解:当D,G,E在一条直线上时,雨棚伞面面积最大,
此时AD=(m).
故答案为:2;
(2)连接DE,如图2所示,
∵DG=2m,GE=1.5m,∠DGE=90°,
∴DE==2.5(m),
∵∠DAE=90°,AE=0.5m,
∴AD=(m),
∵AB=5m,
∴雨棚伞面的面积是:AB AD=5×=5(m2),
故答案为:5.
【点睛】本题考查了勾股定理的应用,解答本题的关键是明确题意,求出矩形的宽.
14. (为整数)
【分析】根据正方形的面积公式求出面积,再根据直角三角形三条边的关系运用勾股定理求出三角形的直角边,求出S1,然后利用正方形与三角形面积扩大与缩小的规律推导出公式.
【详解】解:(1)∵第一个正方形的边长为1,
∴正方形的面积为1,
又∵直角三角形一个角为30°,
∴三角形的一条直角边为,另一条直角边就是,
∴三角形的面积为,
∴S1=;
(2)∵第二个正方形的边长为,它的面积就是,也就是第一个正方形面积的,
同理,第二个三角形的面积也是第一个三角形的面积的,
∴S2=() ,
依此类推,S3=() ,
即S3=() ,
Sn=(n为整数).
故答案为:(1) ;(2)(为整数)
【点睛】本题考查勾股定理的运用,正方形的性质以及含30°角的直角三角形的性质.能够发现每一次得到的新的正方形和直角三角形的面积与原正方形和直角三角形的面积之间的关系是解题的关键.
15.
【分析】延长,过点作的垂线,垂足为点,根据和的面积相等可知线段AD是中线,,根据直角三角形的勾股定理可得的长度.
【详解】解:延长,过点作的垂线,垂足为点,如图所示
∵和的面积相等
∴
∵
∴
∵根据三角形中线的性质可知
∴
∵
∴
∴在中可得
在中可得
∴
∴在中可得
故答案为:
【点睛】本题考查了三角形的中线和面积的关系以及勾股定理等知识点,灵活运用三角形的中线和面积的关系是解题的关键.
16. 2 见解析
【分析】(1)根据三角形的面积公式,即可求出答案;
(2)根据题意,在BC上取BD=3CD,即可画出图形.
【详解】解:(1);
(2)如图:找BC的四等分点,连接AD为所求.
作法:①取线段,在线段取一点,使.
②过所作的平行线,使,交于点.
③作直线
则直线就是所求作的直线.
【点睛】本题考查了复杂作图,以及三角形的面积,解题的关键是学会利用分割法求三角形面积,巧妙利用格点作四等分点,属于作图中比较难的题目.
17.7
【分析】根据勾股定理求得,进而求得,再求得,即可求解.
【详解】解:,
,
……
,
,
……
,
.
故答案为:.
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
18.116
【分析】过点A作,交BC于点H,根据等腰直角三角形的性质可得:,利用三角形面积公式可得:,然后根据勾股定理得出:,根据题意BD:DC=2:5,结合,可得,,在中,利用勾股定理可得正方形的边长,根据正方形面积公式即可求出面积.
【详解】解:过点A作,交BC于点H,
∴,
∵等腰直角的面积等于98,
∴,
∴,
又∵BD:DC=2:5,
∴,,
在中,
,
∴正方形ABCD的面积:.
故本题答案为:116.
【点睛】题目主要考查等腰直角三角形的性质、线段比及勾股定理,作出辅助线应用勾股定理是解题关键.
19.
【分析】先利用勾股定理计算的长,再利用长方形的面积公式进行计算即可.
【详解】解:∵,
∴.
∴阴影部分的面积为.
【点睛】本题考查的是勾股定理的应用,熟记勾股定理并灵活运用是解本题的关键.
20.(1)30;(2)4.
【分析】(1)根据勾股定理的逆定理得到∠ADC=90°,根据三角形的面积公式计算即可;
(2)根据勾股定理计算,得到答案.
【详解】解:(1)∵AB=13,BD=8,
∴AD=AB﹣BD=5,
∴AC=13,CD=12,
∴AD2+CD2=AC2,
∴∠ADC=90°,即△ADC是直角三角形,
∴△ADC的面积=×AD×CD=×5×12=30;
(2)在Rt△BDC中,∠BDC=180°﹣90°=90°,
由勾股定理得:BC==4,即BC的长是4.
【点睛】此题主要考查勾股定理的应用,解题的关键是熟知直角三角形的性质及勾股定理的应用.
21.(1)a2+b2= ( a+b) 2-2ab;
(2).
【分析】(1)分别用两种不同的方法表示阴影部分面积即可得等式.
(2)先直接用c表示中间正方形的面积,再用大正方形的面积减去4个小三角形的面积表示中间正方形的面积,从而可得结论.
【详解】(1)解∶如图1,∵ S阴影=a2+b2,S阴影= ( a+b) 2-2ab .
∴a2+b2= ( a+b) 2-2ab,
故答案为∶a2+b2= ( a+b) 2-2ab;
(2)解:如图2,∵S中间正方形=c2,S中间正方形=(a+b)2-4×ab,
∴,
∴.
【点睛】本题考查完全平方公式及勾股定理的几何背景,用两种方法表示同一个图形的面积是求解本题的关键.
22.(1)
(2)
【分析】(1)求出,利用勾股定理求出的长;
(2)先求出,根据的面积是面积的得,计算即可;
【详解】(1)解:当出发2秒后,,
∴,
∵,
∴
(2)解:∵,
∴,
∴,
得.
【点睛】此题考查了勾股定理,三角形与动点问题,实际问题与一元一次方程,列比例求解,解题中运用分类思想,正确掌握勾股定理的计算公式是解题的关键.
23.的面积为84
【分析】根据题意和题目中的数据,利用勾股定理可以列出相应的方程,然后求出BD的长,再求出AD的长,即可计算出△ABC的面积.
【详解】设BD的长为x,则CD的长为14 - x,
∵AD⊥BC,
∴∠ADB=∠ADC=90°
∴AD2= AB2- BD2
AD2= AC2- CD2.
∴AB2- BD2 = AC2- CD2,
∵AB= 13, AC= 15,
∴132-x2=152-(14- x)2,
解得x = 5,
∴BD=5,CD=14-x=9,
∴AD2= 132- 52,
解得AD= 12,
∴S△ABC =
即△A BC的面积是84.
【点睛】本题考查勾股定理的应用,解答本题的关键是求出BD和AD的长.
24.(1)5
(2)①;②四边形CADB的面积为定值,为16
【分析】(1)直接根据勾股定理,即可求解;
(2)①根据勾股定理可得,,可得,再由,即可求解;②根据,即可求解.
【详解】(1)解:根据勾股定理,得:斜边长为;
故答案为:5
(2)解:①∵ ,
∴,
∵∠D=90°,
∴,
∵AD=BD,
∴,
∴,
∴;
故答案为:
②四边形CADB的面积为为定值,理由如下:
=16
【点睛】本题主要考查了勾股定理的应用,完全平方公式的应用,明确题意,理解勾股定理是解题的关键.
25.(1)见解析
(2)
(3)25
【分析】(1)如图1所示,大正方形的面积等于四个全等的直角三角形面积与小正方形面积和,用代数式表示出各部分面积按要求列等式化简即可得证;
(2)利用勾股定理得到,根据等面积法列式求解即可得到;
(3)由(1)的结论,结合完全平方公式变形,代值求解即可得到答案.
【详解】(1)解:如图1所示:
大正方形的面积等于四个全等的直角三角形面积与小正方形面积和,
;;;
,即;
(2)解:如图2所示:
在中,,,
∴由勾股定理可得,
是边上的高,
由等面积法可得,
,,
∴;
(3)解:∵大正方形的面积是13,小正方形的面积是1,,如图1所示:
∴,
∴,
由(1)知,
∴,
∴,即的值为25.
【点睛】本题考查等面积法解决问题,涉及勾股定理证明、等面积法求线段长、以及完全平方公式与勾股定理综合,熟练掌握等面积法求解是解决问题的关键.
26.(1)30
(2)60
(3)15
【分析】(1)根据勾股定理的逆定理判断△ABC是直角三角形,再求面积即可;
(2)作AD⊥BC于D,由等腰三角形三线合一的性质及勾股定理求出AD的长度,再根据面积公式计算即可;
(3)作CD⊥AB于D,先由勾股定理计算出CD的长度,再根据面积公式计算即可.
【详解】(1)∵AC=5,BC=12,AB=13,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°,
∴△ABC的面积=AC×BC=×5×12=30;
故答案为:30;
(2)作AD⊥BC于D,如图2所示:
∵AB=AC,
∴BD=CD=BC=5,
∴AD===12,
∴△ABC的面积=BC×AD=×10×12=60;
(3)作CD⊥AB于D,如图3所示:
由勾股定理得:CD2=AC2﹣AD2=BC2﹣BD2,即82﹣AD2=102﹣(12﹣AD)2,
解得:AD=,
∴CD==,
∴△ABC的面积=AB×CD=×12×=15.
【点睛】本题考查了勾股定理及其逆定理、等腰三角形的性质,熟练掌握知识点是解题的关键.
27.(1)
(2)等腰直角三角形
(3)2
【分析】(1)利用矩形和三角形的面积公式即可得到结论;
(2)利用网格计算,,长度进行判断三角形的形状;
(3)利用同底等高的三角形的面积相等解题即可.
【详解】(1)解:
故答案为:.
(2)解:∵,,
∴,
∴是等腰直角三角形
故答案为:等腰直角三角形.
(3)过点C作,则平行线上的点与A、B形成的三角形面积都等于的面积,即网格中满足条件的格点D共有个,
故答案为:.
【点睛】本题考查三角形的面积,三角形的形状,应用数形结合的思想解决问题是解题的关键.
28.(1)150;(2)66;(3)84
【分析】(1)根据勾股定理求出,求出,根据勾股定理的逆定理得出△ADB是直角三角形,根据勾股定理求出CD,求出BC,再求出△ABC的面积即可;
(2)过E作EM⊥FG,交GF的延长线于M,设FM=x,则GM=11+x,根据勾股定理得出,代入求出x,再求出EM,最后求出△EFG的面积即可;
(3)过点E作EH⊥FG于点H,由勾股定理可得,从而可得,设FH=x,则GH=14-x,即,再求出EH,即可求解.
【详解】解:(1),,,
,,
,
是直角三角形,
即,
,
由勾股定理得:,
,
的面积;
(2)过作,交的延长线于,设,则,
在和中,由勾股定理得:,,
,
,
解得:,
即,
,
的面积.
(3)解:如图,过点作于点,
在和中,由勾股定理可得:
,,
,
设,则,
,,,
,
解得:,
,
,
的面积为84
【点睛】本题考查了勾股定理,勾股定理的逆定理和三角形的面积等知识点,能熟记勾股定理的逆定理是解此题的关键,注意:如果一个三角形的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形.
29.(1)见解析
(2)
【分析】(1)根据题目所给条件证即可;
(2)由可得,由勾股定理可求BD,即可求解;
【详解】(1)证明:∵,
∴,
∵,
∴.
(2)解:∵,
∴,
在中,,
∴.
【点睛】本题主要考查三角形的全等证明、勾股定理,掌握三角形的全等证明及性质是解题的关键.
30.(1)a2+b2,ab;(2)四个三角形的面积相等;(3)S=T.
【分析】(1)根据题意,可以证得中间的两个三角形全等,再根据勾股定理,即可得出答案;
(2)求出两个钝角三角形的底边和高,然后根据三角形的面积公式求解即可;
(3)利用勾股定理分别求出S和T的值,然后比较求解即可.
【详解】(1)如图1所示:∵三个四边形均为正方形,
∴∠ACB+∠BAC=90°,∠ACB+∠DCE=90°,AC=CE,
∴∠BAC=∠DCE,
∵∠ABC=∠CDE=90°,
∴△ABC≌△CDE,
∴BC=DE=b,AB=CD=a,
∴S△ABC+S△CDE=ab,
同时AC2=AB2+BC2,
∵两个正方形的面积分别为a2,b2,
∴S=a2+b2,
(2)如图2所示,a=1,斜正方形边长c=2,b=,
由30°角和60°角易求出面积为m1的三角形底边长为1,高为,故m1=;
面积为m2的三角形边长为,高为1,故m2=.
结论:四个三角形的面积相等.
(3)S=T.如图3所示,首先由(2)知:T=S△ABC,
设小正方形边长为a,大正方形边长为b,
由(1)知:S=a2+b2,又图中四个小三角形的面积m=ab,
S△ABC=a2+b2+(a2+b2)+4×ab﹣(a+b)(2a+2b)=a2+b2=S,
∴S=T.
【点睛】本题考查了勾股定理的运用,结合正方形的面积求解公式求解.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
