专题1.21勾股定理中的方程思想 分层练习(含解析)2023-2024学年八年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.21勾股定理中的方程思想 分层练习(含解析)2023-2024学年八年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 921.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览



文档简介
专题1.21 勾股定理中的方程思想(分层练习)
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习
1.的三边长分别为,,,若该三角形是以为斜边的直角三角形,求的值.
2.在中,,、、的边分别为a、b、c.
(1)若,,求a,b的值.
(2)若,,求a的值.
3.如图,在中,,,,动点P从点B出发沿射线以的速度移动,设运动的时间为t秒.
(1)用含t的代数式表示
①当点P在线段上时,________.
②当点P在线段的延长线上时,________.
(2)当为直角三角形时,求t的值;
4.春天到了,奇奇和妙妙一同去春游.如图,有一座景观桥,他俩一同坐在离桥头A的凉亭D处,准备从桥的不同方向到达景点C.奇奇先走到桥尾B到岸边后再坐船到景点C,妙妙先走到桥头A到岸边,再沿与桥垂直的小路走到达景点C,若距离均以直线计算,且两人所经过的距离相等,请利用所学知识计算桥的长是多少?
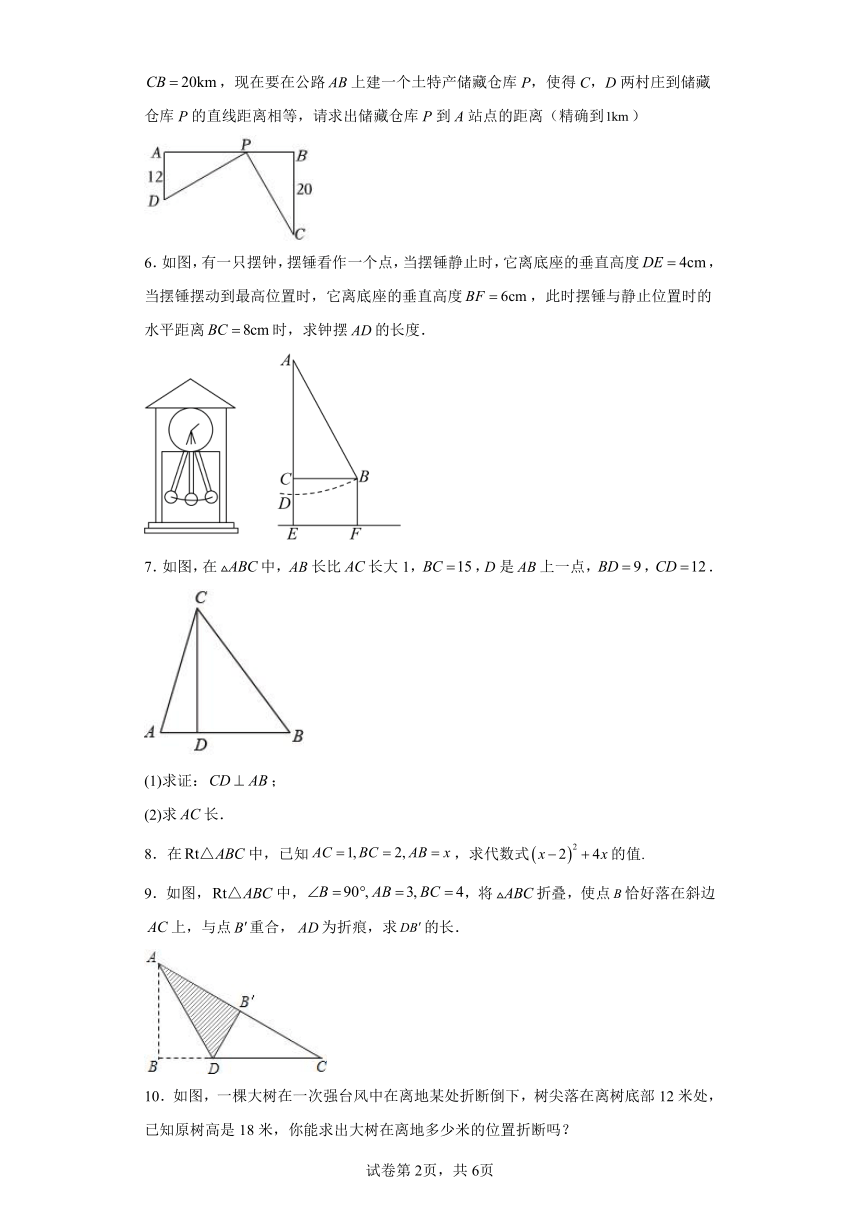
5.一条东西走向的公路上有A,B两个站点(视为直线上的两点)相距,C,D为两村庄(视为两个点),于点A,于点(如图),已知,,现在要在公路上建一个土特产储藏仓库P,使得C,D两村庄到储藏仓库P的直线距离相等,请求出储藏仓库P到A站点的距离(精确到)
6.如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度,当摆锤摆动到最高位置时,它离底座的垂直高度,此时摆锤与静止位置时的水平距离时,求钟摆的长度.
7.如图,在中,长比长大1,,D是上一点,,.
(1)求证:;
(2)求长.
8.在中,已知,求代数式的值.
9.如图,中,,将折叠,使点恰好落在斜边上,与点重合,为折痕,求的长.
10.如图,一棵大树在一次强台风中在离地某处折断倒下,树尖落在离树底部12米处,已知原树高是18米,你能求出大树在离地多少米的位置折断吗?
11.如图,某斜拉桥的主梁垂直于桥面与点D,主梁上有两根拉索分别为.
(1)若拉索的长度分别为10米、26米,则拉索______米,主梁______米;
(2)若的长分别为13米、20米,且固定点B、C之间的距离为21米,求主梁AD的高度.
12.《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地四尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有4尺.牵着绳索(绳索头与地面接触)退行,在距木根部8尺处时绳索用尽,问绳索长是多少?根据题意求出绳索长.
13.同学们想利用升旗的绳子、卷尺,测算学校旗杆的高度.爱动脑的小华设计了这样一个方案:如图,将升旗的绳子拉直刚好触底,此时测得绳子末端C到旗杆AB的底端B的距离为1米,然后将绳子末端拉直到距离旗杆5米的点E处,此时测得绳子末端E距离地面的高度为1米.请你根据小华的测量方案和测量数据,求出学校旗杆的高度.
14.如图所示,有一根高为的电线杆在处断裂,电线杆顶部C落在地面离电线杆底部B点远的地方,求电线杆断裂处A离地面的距离.
15.光武大桥是我市中心城区的首座斜拉大桥,为纪念故乡南阳的东汉光武帝刘秀而命名,若一根斜拉钢梁竖直垂下时底端在桥下面的5米处,当点固定在桥面上的处时,距离点15米,求这根钢梁的长度.
16.如图,小巷左右两侧是竖直的高度相等的墙,一根竹竿斜靠在左墙时,竹竿底端O到左墙角的距离为米,顶端B距墙顶的距离为米若保持竹竿底端位置不动,将竹竿斜靠在右墙时,竹竿底端到右墙角的距离为米,顶端E距墙项D的距离为1米,点A、B、C在一条直线上,点D、E、F在一条直线上,,.求:
(1)墙的高度;
(2)竹竿的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙寸,点C、点D与门槛的距离尺(1尺=10寸),O是的中点,连接.
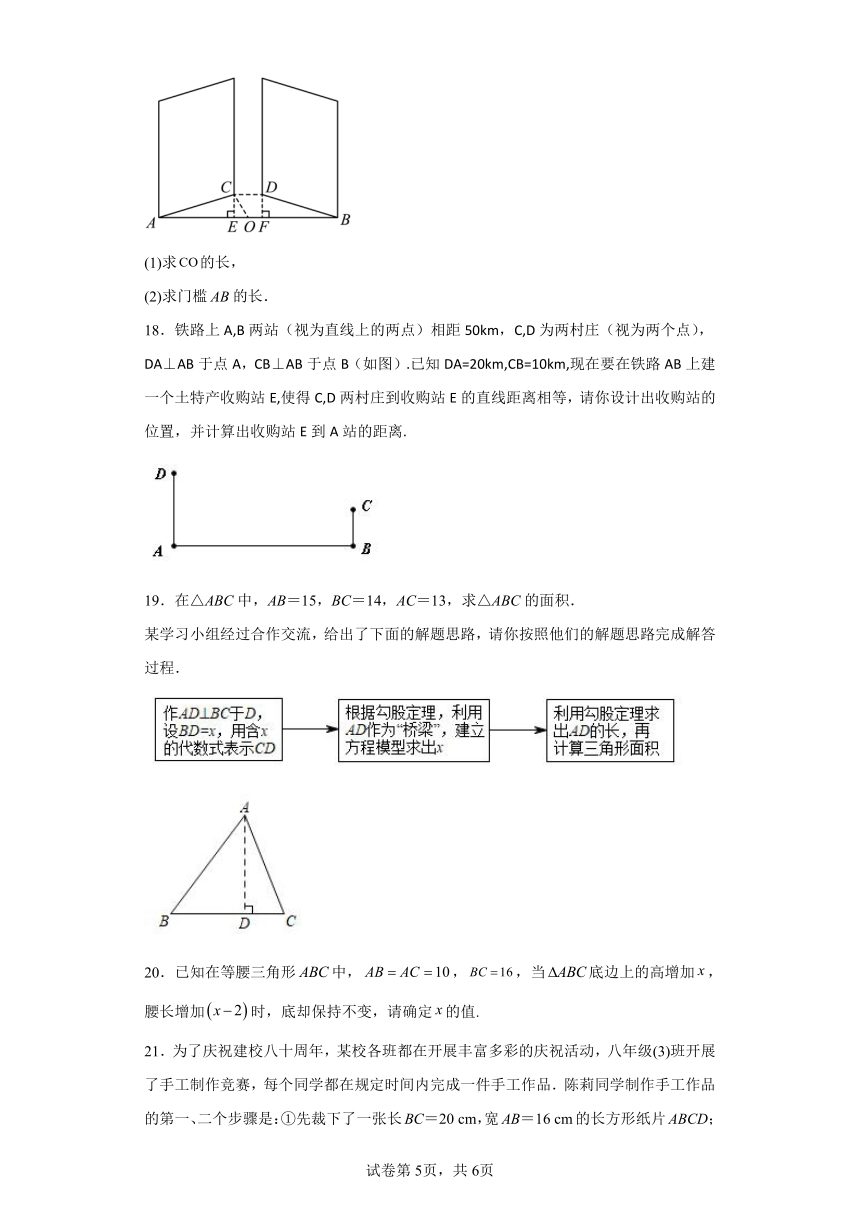
(1)求的长,
(2)求门槛的长.
18.铁路上A,B两站(视为直线上的两点)相距50km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B(如图).已知DA=20km,CB=10km,现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的直线距离相等,请你设计出收购站的位置,并计算出收购站E到A站的距离.
19.在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
20.已知在等腰三角形中,,,当底边上的高增加,腰长增加时,底却保持不变,请确定的值.
21.为了庆祝建校八十周年,某校各班都在开展丰富多彩的庆祝活动,八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;②将纸片沿着直线AE折叠,使点D恰好落在BC边上的F处……请你根据①②步骤解答下列问题.
(1)找出图中的∠FEC的余角;
(2)计算EC的长.
22.已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
23.在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.
【分析】利用直角三角形勾股定理得性质,列出方程,借用方程解出x即可.
【详解】解:∵该三角形是以为斜边的直角三角形,
∴,
∴.
【点睛】本题考查了勾股定理,能利用勾股定理列出方程是解答此题的关键.
2.(1),
(2)30
【分析】(1)设,则,再根据勾股定理求出的值,进而可得出结论.
(2)根据勾股定理可得,,的数量关系,再把已知条件代入即可求出的值.
【详解】(1)解:中,,、、的对边分别为、、,且,
设,则.
,即,
解得(负值舍去),
,;
(2)中,,,,的对边分别为,,,
,
,,
,
解得:.
【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
3.(1)① ;②
(2)或
【分析】(1)先根据勾股定理求出的长度,然后再根据图形求解即可;
(2)当为直角三角形时,分两种情况:①当为直角时,②当为直角时,分别求出此时的t值即可.
【详解】(1)∵,,,
∴.
∵动点P从点B出发沿射线以的速度移动,
∴.
①当点P在线段上时,.
②当点P在线段的延长线上时,.
故答案为:①;②;
(2)①当为直角时,点P与点C重合,,即;
②当为直角时,,,
在中,,
在中,,
即:,
解得,
故当为直角三角形时,或;
【点睛】本题考查了勾股定理,解答本题的关键是掌握勾股定理,以及分情况讨论.
4.桥长.
【分析】设桥长为,则,利用两人所经过的距离相等,求得,在中,利用勾股定理列式计算即可求解.
【详解】解:设桥长为,则,由题可知,,
∴,
∴,
∵为直角三角形,
∴,
∴,
解得,
答:桥长.
【点睛】本题考查了勾股定理的应用,能从实际问题中抽象出勾股定理并应用解决问题是关键.
5.
【分析】由题意得,再由勾股定理得,设AP为x km,则,得方程,解方程即可.
【详解】解:、D两村到储藏仓库P的直线距离相等,
,
,,
,
在和中,由勾股定理得:,,
,
设,则,
,
解得:,
答:储藏仓库P到A站点的距离约为
【点睛】本题考查了勾股定理的应用,由勾股定理得出方程是解题的关键.
6.
【分析】设,表示出的长,然后利用勾股定理列方程求解即可.
【详解】设,由题意得, ,
∴,
∵,
∴,
∴,
∴.
【点睛】此题考查了勾股定理的应用,在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
7.(1)见解析
(2)13
【分析】(1)根据,,,得到,根据勾股定理逆定理即可得到,问题得证;
(2)设,则,根据勾股定理得到,解方程即可求解.
【详解】(1)证明:,,,
∴ ,,
∴,
,
;
(2)解:由题意得,
设,则,
,
,
,
解得:,
即.
【点睛】本题考查了勾股定理及其逆定理,熟知两个定理并根据题意灵活应用是解题关键.
8.9或7
【分析】分两种情况讨论①当是斜边时,②当是斜边时,即可求解.
【详解】解:由题意得:,
①当是斜边时,
则,
即,
解得:,
∴,
②当是斜边时,
则,
即,
解得:,
∴,
综上所述:代数式的值为9或7.
【点睛】本题考查了求代数式的值,核心是考查勾股定理,掌握分类讨论思想是解题关键.
9.
【分析】根据勾股定理得到,由折叠的性质得到,设,则,根据勾股定理即可得到结论.
【详解】解:在中,,
∴,
∵将折叠,使点B恰好落在斜边上,与点重合,
∴,
∴,
设,则,
∵在中,,
∴,
解得,
∴.
【点睛】本题考查了翻折变换-折叠问题,勾股定理,熟练掌握折叠的性质是解题的关键.
10.5米
【分析】设大树在离地米处折断,则折断处离树尖的距离为米,再根据勾股定理建立方程求解即可.
【详解】解:设大树在离地米处折断,
由勾股定理得:,
解得.
答:大树在离地5米的位置折断.
【点睛】本题主要考查了勾股定理的实际应用,正确理解题意并熟知勾股定理是解题的关键.
11.(1)24,
(2)主梁的高度为12米
【分析】(1)根据勾股定理可求得,再根据等面积法可求得;
(2)设米,则米,由题意可得,则、可得解得:,最后在中运用勾股定理即可解答.
【详解】(1)解:∵的长度分别为10米、26米,
∴(米),
∵
∴,解得:(米).
(2)解:设米,则米,
∵主梁垂直于桥面于点,
∴,
∴根据勾股定理可得:,
∴,解得:
∵,
∴.
答:主梁的高度为12米.
【点睛】本题主要考查了运用勾股定理解直角三角形、勾股定理的的应用等知识点,根据勾股定理建立方程是解答本题的关键.
12.绳索长为10尺
【分析】设绳索长为x尺,利用勾股定理进行求解即可.
【详解】解:设绳索长为x尺,根据题意得:
,
解得:,
答:绳索长为10尺.
【点睛】本题考查勾股定理的应用.熟练掌握勾股定理,是解题的关键.
13.12.5米
【分析】过点E作,垂足为F,在和中,根据勾股定理得出,,根据,得出,求出的长即可.
【详解】解:过点E作,垂足为F,如图所示:
由题意可知:四边形是长方形,和是直角三角形,
∴,,,
在和中,根据勾股定理可得:
,,
即,,
又∵,
∴,
解得:.
答:学校旗杆的高度为12.5米.
【点睛】本题主要考查了勾股定理的应用,解题的关键是根据勾股定理列出关于方程.
14.
【分析】根据题意,设,则.运用勾股定理,列方程求解即可.
【详解】解:设,则.
根据勾股定理,得,
∴,
∴,
解得:.
∴
【点睛】本题考查了勾股定理的应用,根据题意建列方程是解题的关键.
15.这根钢梁的长度为25米.
【分析】设米,由题意得到:,,根据一根斜拉钢梁竖直垂下,利用勾股定理建立等式求解.
【详解】解:设米,由题意得到:,,
一根斜拉钢梁竖直垂下,
,
,
,
解得:米
答:这根钢梁的长度为25米.
【点睛】本题考查了勾股定理,解题的关键是得出是直角三角形,利用勾股定理求解.
16.(1)墙高3米
(2)竹竿的长米
【分析】(1)设墙高x米,在,根据勾股定理即可表示出竹竿长度的平方 ,联立即可得到答案;
(2)把(1)中的x代入勾股定理即可得到答案.
【详解】(1)解:设墙高x米,
∵,,
∴ ,
在,根据勾股定理可得,
,,
∵ ,
∴,
解得: ,
答:墙高3米;
(2)由(1得),
, ,
∴
答:竹竿的长米.
【点睛】本题考查勾股定理实际应用题,解题的关键时根据两种不同状态竹竿长不变列等式及正确计算.
17.(1)
(2)
【分析】(1)根据题意得到,然后根据勾股定理求解即可;
(2)由题意可得,设,则,利用勾股定理即可求解.
【详解】(1)解:∵O是的中点
∴
∵
∴;
(2)设,则.
∵, 尺寸
∴
解得:
∴.
【点睛】本题考查了勾股定理的应用,弄清题意,构建直角三角形是解题关键.
18.收购站E到A站的距离为22km
【详解】分析:连接CD,并作线段CD的垂直平分线,垂直平分线到端点距离相等,再利用勾股定理求EA长.
点睛:
如图,连接CD,并作线段CD的垂直平分线,与AB相交于点E,点E即为所建土特产收购站的地点.
连接DE,CE ,设AE=x km, 则BE=(50-x) km ,
在Rt△ADE中,,
∴ ,
在Rt△BCE中, ,
∴,
又DE=CE, ∴ ,
解得x=22 .
∴收购站E到A站的距离为22km.
点睛:
勾股定理:在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方.
19.84.
【详解】解:作AD⊥BC于D,
如图所示:设BD = x,则.
在Rt△ABD中,由勾股定理得:,
在Rt△ACD中,由勾股定理得:,
∴ ,
解之得:.
∴.
∴ .
20..
【分析】过点作于点.先根据勾股定理求出AD的长,然后根据变化后的边长利用勾股定理列方程解答即可.
【详解】过点作于点.
因为,,所以.
在中,,所以.
根据题意得,,
所以.
【点睛】此题考查勾股定理,关键是根据勾股定理和等腰三角形的性质解答.在直角三角形中,如果两条直角边分别为a和b,斜边为c,那么a2+b2=c2.也就是说,直角三角形两条直角边的平方和等于斜边的平方.
21.(1)∠CFE、∠BAF;(2) 6 cm.
【分析】(1)结合图形易得∠CFE+∠FEC=90°,由于∠CFE+∠AFB=90°,故∠FEC=∠AFB,故∠BAF+∠FEC=90°,故可得答案;
(2)设EC=xcm,可得EF的长度,根据折叠的性质可得AF=AD.在Rt△EFC中使用勾股定理,可得EF2=FC2+EC2,解可得x的值,即EC的长度.
【详解】解:(1)∠CFE、∠BAF;
(2)设EC=xcm,则EF=DE=(16﹣x)cm.
∵AF=AD=20cm,
∴在Rt△ABF中,BF==12(cm),FC=BC﹣BF=20﹣12=8(cm).
在Rt△EFC中,EF2=FC2+EC2,(16﹣x)2=82+x2,x=6.
∴EC的长为6cm.
【点睛】本题综合考查了矩形与折叠,及勾股定理的运用.
22.
【分析】先根据等腰三角形的性质和勾股定理求出AE=6,设BD=x,则DE=8﹣x,DC=16﹣x.在Rt△ADE和Rt△ADC中利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,继而代入求出x的值即可.
【详解】如图,过点A作AE⊥BC于点E,
∵AB=AC=10,BC=16,∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE===6,
设BD=x,则DE=8﹣x,DC=16﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,
代入为:62+(8﹣x)2=(16﹣x)2﹣102,解得:x=.
即BD=.
【点睛】本题考查了勾股定理及等腰三角形的性质,解题的关键是在Rt△ADE和Rt△ADC中分别利用勾股定理,列出等式AD2=AE2+DE2=DC2﹣AC2.
23.S△ABC=84.
【分析】设BD=x,则有CD=14﹣x,根据AD2=AB2﹣BD2,AD2=AC2﹣CD2,列出方程求解即可得到答案.
【详解】解:如图,在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
∴152﹣x2=132﹣(14﹣x)2,
解之得:x=9,
∴AD=12,
∴S△ABC=BC AD=×14×12=84.
【点睛】本题主要考查了勾股定理和利用方程的思想解决问题,三角形的面积公式,解题的关键在于能够熟练掌握勾股定理.
答案第1页,共2页
答案第1页,共2页
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习
1.的三边长分别为,,,若该三角形是以为斜边的直角三角形,求的值.
2.在中,,、、的边分别为a、b、c.
(1)若,,求a,b的值.
(2)若,,求a的值.
3.如图,在中,,,,动点P从点B出发沿射线以的速度移动,设运动的时间为t秒.
(1)用含t的代数式表示
①当点P在线段上时,________.
②当点P在线段的延长线上时,________.
(2)当为直角三角形时,求t的值;
4.春天到了,奇奇和妙妙一同去春游.如图,有一座景观桥,他俩一同坐在离桥头A的凉亭D处,准备从桥的不同方向到达景点C.奇奇先走到桥尾B到岸边后再坐船到景点C,妙妙先走到桥头A到岸边,再沿与桥垂直的小路走到达景点C,若距离均以直线计算,且两人所经过的距离相等,请利用所学知识计算桥的长是多少?
5.一条东西走向的公路上有A,B两个站点(视为直线上的两点)相距,C,D为两村庄(视为两个点),于点A,于点(如图),已知,,现在要在公路上建一个土特产储藏仓库P,使得C,D两村庄到储藏仓库P的直线距离相等,请求出储藏仓库P到A站点的距离(精确到)
6.如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度,当摆锤摆动到最高位置时,它离底座的垂直高度,此时摆锤与静止位置时的水平距离时,求钟摆的长度.
7.如图,在中,长比长大1,,D是上一点,,.
(1)求证:;
(2)求长.
8.在中,已知,求代数式的值.
9.如图,中,,将折叠,使点恰好落在斜边上,与点重合,为折痕,求的长.
10.如图,一棵大树在一次强台风中在离地某处折断倒下,树尖落在离树底部12米处,已知原树高是18米,你能求出大树在离地多少米的位置折断吗?
11.如图,某斜拉桥的主梁垂直于桥面与点D,主梁上有两根拉索分别为.
(1)若拉索的长度分别为10米、26米,则拉索______米,主梁______米;
(2)若的长分别为13米、20米,且固定点B、C之间的距离为21米,求主梁AD的高度.
12.《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地四尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有4尺.牵着绳索(绳索头与地面接触)退行,在距木根部8尺处时绳索用尽,问绳索长是多少?根据题意求出绳索长.
13.同学们想利用升旗的绳子、卷尺,测算学校旗杆的高度.爱动脑的小华设计了这样一个方案:如图,将升旗的绳子拉直刚好触底,此时测得绳子末端C到旗杆AB的底端B的距离为1米,然后将绳子末端拉直到距离旗杆5米的点E处,此时测得绳子末端E距离地面的高度为1米.请你根据小华的测量方案和测量数据,求出学校旗杆的高度.
14.如图所示,有一根高为的电线杆在处断裂,电线杆顶部C落在地面离电线杆底部B点远的地方,求电线杆断裂处A离地面的距离.
15.光武大桥是我市中心城区的首座斜拉大桥,为纪念故乡南阳的东汉光武帝刘秀而命名,若一根斜拉钢梁竖直垂下时底端在桥下面的5米处,当点固定在桥面上的处时,距离点15米,求这根钢梁的长度.
16.如图,小巷左右两侧是竖直的高度相等的墙,一根竹竿斜靠在左墙时,竹竿底端O到左墙角的距离为米,顶端B距墙顶的距离为米若保持竹竿底端位置不动,将竹竿斜靠在右墙时,竹竿底端到右墙角的距离为米,顶端E距墙项D的距离为1米,点A、B、C在一条直线上,点D、E、F在一条直线上,,.求:
(1)墙的高度;
(2)竹竿的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙寸,点C、点D与门槛的距离尺(1尺=10寸),O是的中点,连接.
(1)求的长,
(2)求门槛的长.
18.铁路上A,B两站(视为直线上的两点)相距50km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B(如图).已知DA=20km,CB=10km,现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的直线距离相等,请你设计出收购站的位置,并计算出收购站E到A站的距离.
19.在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
20.已知在等腰三角形中,,,当底边上的高增加,腰长增加时,底却保持不变,请确定的值.
21.为了庆祝建校八十周年,某校各班都在开展丰富多彩的庆祝活动,八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;②将纸片沿着直线AE折叠,使点D恰好落在BC边上的F处……请你根据①②步骤解答下列问题.
(1)找出图中的∠FEC的余角;
(2)计算EC的长.
22.已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
23.在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.
【分析】利用直角三角形勾股定理得性质,列出方程,借用方程解出x即可.
【详解】解:∵该三角形是以为斜边的直角三角形,
∴,
∴.
【点睛】本题考查了勾股定理,能利用勾股定理列出方程是解答此题的关键.
2.(1),
(2)30
【分析】(1)设,则,再根据勾股定理求出的值,进而可得出结论.
(2)根据勾股定理可得,,的数量关系,再把已知条件代入即可求出的值.
【详解】(1)解:中,,、、的对边分别为、、,且,
设,则.
,即,
解得(负值舍去),
,;
(2)中,,,,的对边分别为,,,
,
,,
,
解得:.
【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
3.(1)① ;②
(2)或
【分析】(1)先根据勾股定理求出的长度,然后再根据图形求解即可;
(2)当为直角三角形时,分两种情况:①当为直角时,②当为直角时,分别求出此时的t值即可.
【详解】(1)∵,,,
∴.
∵动点P从点B出发沿射线以的速度移动,
∴.
①当点P在线段上时,.
②当点P在线段的延长线上时,.
故答案为:①;②;
(2)①当为直角时,点P与点C重合,,即;
②当为直角时,,,
在中,,
在中,,
即:,
解得,
故当为直角三角形时,或;
【点睛】本题考查了勾股定理,解答本题的关键是掌握勾股定理,以及分情况讨论.
4.桥长.
【分析】设桥长为,则,利用两人所经过的距离相等,求得,在中,利用勾股定理列式计算即可求解.
【详解】解:设桥长为,则,由题可知,,
∴,
∴,
∵为直角三角形,
∴,
∴,
解得,
答:桥长.
【点睛】本题考查了勾股定理的应用,能从实际问题中抽象出勾股定理并应用解决问题是关键.
5.
【分析】由题意得,再由勾股定理得,设AP为x km,则,得方程,解方程即可.
【详解】解:、D两村到储藏仓库P的直线距离相等,
,
,,
,
在和中,由勾股定理得:,,
,
设,则,
,
解得:,
答:储藏仓库P到A站点的距离约为
【点睛】本题考查了勾股定理的应用,由勾股定理得出方程是解题的关键.
6.
【分析】设,表示出的长,然后利用勾股定理列方程求解即可.
【详解】设,由题意得, ,
∴,
∵,
∴,
∴,
∴.
【点睛】此题考查了勾股定理的应用,在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
7.(1)见解析
(2)13
【分析】(1)根据,,,得到,根据勾股定理逆定理即可得到,问题得证;
(2)设,则,根据勾股定理得到,解方程即可求解.
【详解】(1)证明:,,,
∴ ,,
∴,
,
;
(2)解:由题意得,
设,则,
,
,
,
解得:,
即.
【点睛】本题考查了勾股定理及其逆定理,熟知两个定理并根据题意灵活应用是解题关键.
8.9或7
【分析】分两种情况讨论①当是斜边时,②当是斜边时,即可求解.
【详解】解:由题意得:,
①当是斜边时,
则,
即,
解得:,
∴,
②当是斜边时,
则,
即,
解得:,
∴,
综上所述:代数式的值为9或7.
【点睛】本题考查了求代数式的值,核心是考查勾股定理,掌握分类讨论思想是解题关键.
9.
【分析】根据勾股定理得到,由折叠的性质得到,设,则,根据勾股定理即可得到结论.
【详解】解:在中,,
∴,
∵将折叠,使点B恰好落在斜边上,与点重合,
∴,
∴,
设,则,
∵在中,,
∴,
解得,
∴.
【点睛】本题考查了翻折变换-折叠问题,勾股定理,熟练掌握折叠的性质是解题的关键.
10.5米
【分析】设大树在离地米处折断,则折断处离树尖的距离为米,再根据勾股定理建立方程求解即可.
【详解】解:设大树在离地米处折断,
由勾股定理得:,
解得.
答:大树在离地5米的位置折断.
【点睛】本题主要考查了勾股定理的实际应用,正确理解题意并熟知勾股定理是解题的关键.
11.(1)24,
(2)主梁的高度为12米
【分析】(1)根据勾股定理可求得,再根据等面积法可求得;
(2)设米,则米,由题意可得,则、可得解得:,最后在中运用勾股定理即可解答.
【详解】(1)解:∵的长度分别为10米、26米,
∴(米),
∵
∴,解得:(米).
(2)解:设米,则米,
∵主梁垂直于桥面于点,
∴,
∴根据勾股定理可得:,
∴,解得:
∵,
∴.
答:主梁的高度为12米.
【点睛】本题主要考查了运用勾股定理解直角三角形、勾股定理的的应用等知识点,根据勾股定理建立方程是解答本题的关键.
12.绳索长为10尺
【分析】设绳索长为x尺,利用勾股定理进行求解即可.
【详解】解:设绳索长为x尺,根据题意得:
,
解得:,
答:绳索长为10尺.
【点睛】本题考查勾股定理的应用.熟练掌握勾股定理,是解题的关键.
13.12.5米
【分析】过点E作,垂足为F,在和中,根据勾股定理得出,,根据,得出,求出的长即可.
【详解】解:过点E作,垂足为F,如图所示:
由题意可知:四边形是长方形,和是直角三角形,
∴,,,
在和中,根据勾股定理可得:
,,
即,,
又∵,
∴,
解得:.
答:学校旗杆的高度为12.5米.
【点睛】本题主要考查了勾股定理的应用,解题的关键是根据勾股定理列出关于方程.
14.
【分析】根据题意,设,则.运用勾股定理,列方程求解即可.
【详解】解:设,则.
根据勾股定理,得,
∴,
∴,
解得:.
∴
【点睛】本题考查了勾股定理的应用,根据题意建列方程是解题的关键.
15.这根钢梁的长度为25米.
【分析】设米,由题意得到:,,根据一根斜拉钢梁竖直垂下,利用勾股定理建立等式求解.
【详解】解:设米,由题意得到:,,
一根斜拉钢梁竖直垂下,
,
,
,
解得:米
答:这根钢梁的长度为25米.
【点睛】本题考查了勾股定理,解题的关键是得出是直角三角形,利用勾股定理求解.
16.(1)墙高3米
(2)竹竿的长米
【分析】(1)设墙高x米,在,根据勾股定理即可表示出竹竿长度的平方 ,联立即可得到答案;
(2)把(1)中的x代入勾股定理即可得到答案.
【详解】(1)解:设墙高x米,
∵,,
∴ ,
在,根据勾股定理可得,
,,
∵ ,
∴,
解得: ,
答:墙高3米;
(2)由(1得),
, ,
∴
答:竹竿的长米.
【点睛】本题考查勾股定理实际应用题,解题的关键时根据两种不同状态竹竿长不变列等式及正确计算.
17.(1)
(2)
【分析】(1)根据题意得到,然后根据勾股定理求解即可;
(2)由题意可得,设,则,利用勾股定理即可求解.
【详解】(1)解:∵O是的中点
∴
∵
∴;
(2)设,则.
∵, 尺寸
∴
解得:
∴.
【点睛】本题考查了勾股定理的应用,弄清题意,构建直角三角形是解题关键.
18.收购站E到A站的距离为22km
【详解】分析:连接CD,并作线段CD的垂直平分线,垂直平分线到端点距离相等,再利用勾股定理求EA长.
点睛:
如图,连接CD,并作线段CD的垂直平分线,与AB相交于点E,点E即为所建土特产收购站的地点.
连接DE,CE ,设AE=x km, 则BE=(50-x) km ,
在Rt△ADE中,,
∴ ,
在Rt△BCE中, ,
∴,
又DE=CE, ∴ ,
解得x=22 .
∴收购站E到A站的距离为22km.
点睛:
勾股定理:在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方.
19.84.
【详解】解:作AD⊥BC于D,
如图所示:设BD = x,则.
在Rt△ABD中,由勾股定理得:,
在Rt△ACD中,由勾股定理得:,
∴ ,
解之得:.
∴.
∴ .
20..
【分析】过点作于点.先根据勾股定理求出AD的长,然后根据变化后的边长利用勾股定理列方程解答即可.
【详解】过点作于点.
因为,,所以.
在中,,所以.
根据题意得,,
所以.
【点睛】此题考查勾股定理,关键是根据勾股定理和等腰三角形的性质解答.在直角三角形中,如果两条直角边分别为a和b,斜边为c,那么a2+b2=c2.也就是说,直角三角形两条直角边的平方和等于斜边的平方.
21.(1)∠CFE、∠BAF;(2) 6 cm.
【分析】(1)结合图形易得∠CFE+∠FEC=90°,由于∠CFE+∠AFB=90°,故∠FEC=∠AFB,故∠BAF+∠FEC=90°,故可得答案;
(2)设EC=xcm,可得EF的长度,根据折叠的性质可得AF=AD.在Rt△EFC中使用勾股定理,可得EF2=FC2+EC2,解可得x的值,即EC的长度.
【详解】解:(1)∠CFE、∠BAF;
(2)设EC=xcm,则EF=DE=(16﹣x)cm.
∵AF=AD=20cm,
∴在Rt△ABF中,BF==12(cm),FC=BC﹣BF=20﹣12=8(cm).
在Rt△EFC中,EF2=FC2+EC2,(16﹣x)2=82+x2,x=6.
∴EC的长为6cm.
【点睛】本题综合考查了矩形与折叠,及勾股定理的运用.
22.
【分析】先根据等腰三角形的性质和勾股定理求出AE=6,设BD=x,则DE=8﹣x,DC=16﹣x.在Rt△ADE和Rt△ADC中利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,继而代入求出x的值即可.
【详解】如图,过点A作AE⊥BC于点E,
∵AB=AC=10,BC=16,∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE===6,
设BD=x,则DE=8﹣x,DC=16﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,
代入为:62+(8﹣x)2=(16﹣x)2﹣102,解得:x=.
即BD=.
【点睛】本题考查了勾股定理及等腰三角形的性质,解题的关键是在Rt△ADE和Rt△ADC中分别利用勾股定理,列出等式AD2=AE2+DE2=DC2﹣AC2.
23.S△ABC=84.
【分析】设BD=x,则有CD=14﹣x,根据AD2=AB2﹣BD2,AD2=AC2﹣CD2,列出方程求解即可得到答案.
【详解】解:如图,在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
∴152﹣x2=132﹣(14﹣x)2,
解之得:x=9,
∴AD=12,
∴S△ABC=BC AD=×14×12=84.
【点睛】本题主要考查了勾股定理和利用方程的思想解决问题,三角形的面积公式,解题的关键在于能够熟练掌握勾股定理.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
