专题1.23勾股定理中的动点问题 分层练习提升练(含解析)2023-2024学年八年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.23勾股定理中的动点问题 分层练习提升练(含解析)2023-2024学年八年级数学上册北师大版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 21:52:59 | ||
图片预览

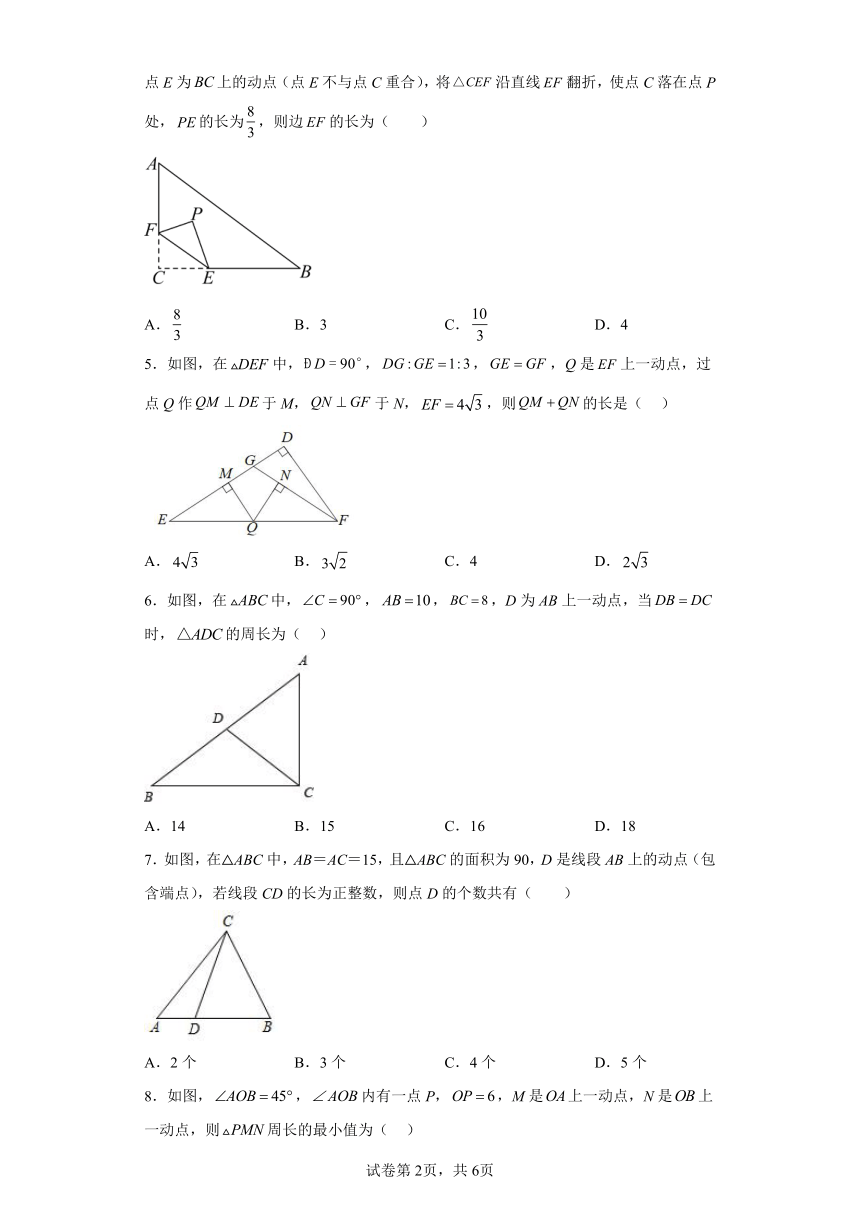

文档简介
专题1.23 勾股定理中的动点问题(分层练习)(提升练)
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习.
一、单选题
1.如图,在△ABC中,∠C=90°,AB=10,BC=8,点P是边BC上的动点,则AP的长不可能为( )
A.5 B.6 C.7 D.9
2.已知Rt△BCE和Rt△ADE按如图方式摆放,∠A=∠B=90°,A、E、B在一条直线上,AD=3,AE=4,EB=5,BC=12,M是线段AD上的动点,N是线段BC上的动点,MN的长度不可能是( )
A.9 B.12 C.14 D.16
3.如图1,动点K从△ABC的顶点A出发,沿AB→BC匀速运动到点C停止,在动点K运动过程中,线段AK的长y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,若△ABC的面积是10 ,则a为( )
A.7 B.2 C.4 D.2
4.如图,在中,,,,点F在AC上,并且,点E为上的动点(点E不与点C重合),将沿直线翻折,使点C落在点P处,的长为,则边的长为( )
A. B.3 C. D.4
5.如图,在中,,,,Q是上一动点,过点Q作于M,于N,,则的长是( )
A. B. C.4 D.
6.如图,在中,,,,D为AB上一动点,当时,的周长为( )
A.14 B.15 C.16 D.18
7.如图,在△ABC中,AB=AC=15,且△ABC的面积为90,D是线段AB上的动点(包含端点),若线段CD的长为正整数,则点D的个数共有( )
A.2个 B.3个 C.4个 D.5个
8.如图,,内有一点P,,M是上一动点,N是上一动点,则周长的最小值为( )
A.6 B.3 C. D.
二、填空题
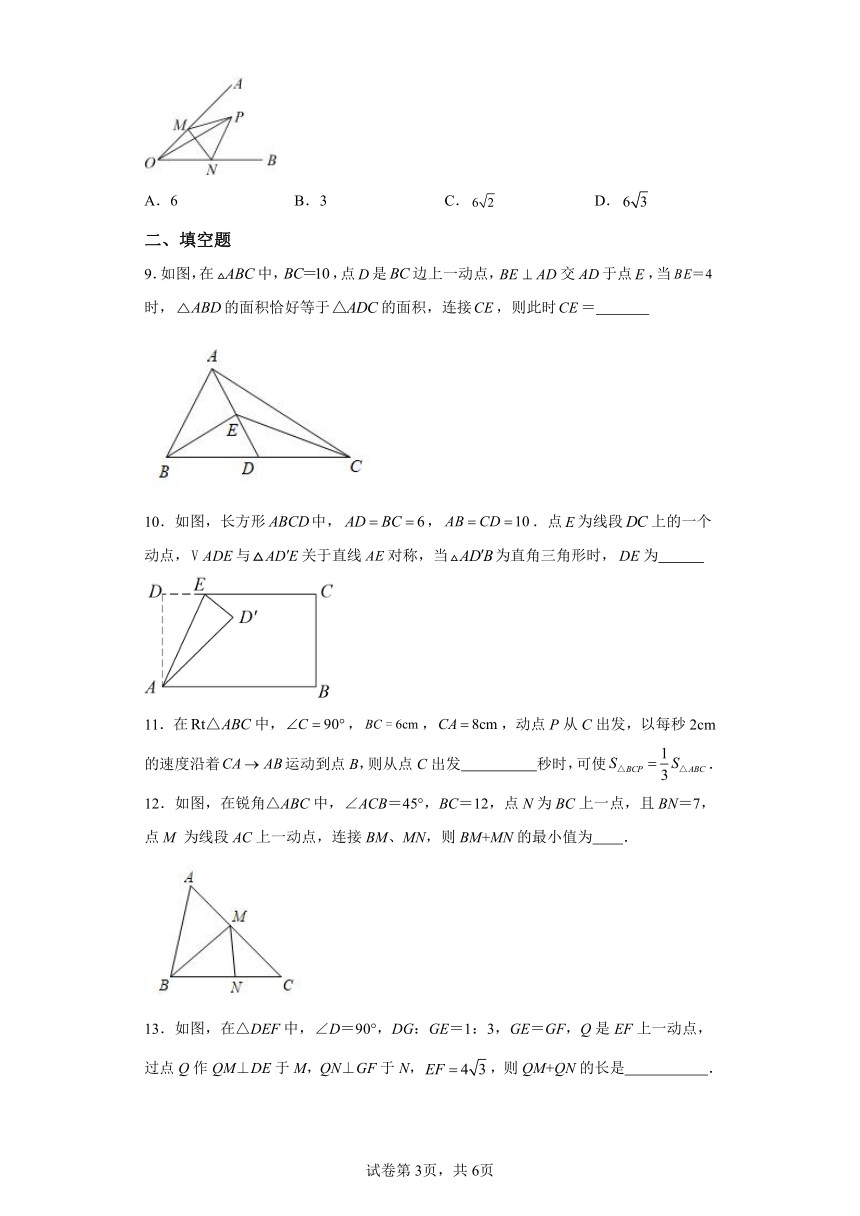
9.如图,在中,,点是边上一动点,交于点,当时,的面积恰好等于的面积,连接,则此时=
10.如图,长方形中,,.点为线段上的一个动点,与关于直线对称,当为直角三角形时,为
11.在中,,,,动点P从C出发,以每秒2cm的速度沿着运动到点B,则从点C出发 秒时,可使.
12.如图,在锐角△ABC中,∠ACB=45°,BC=12,点N为BC上一点,且BN=7,点M 为线段AC上一动点,连接BM、MN,则BM+MN的最小值为 .
13.如图,在△DEF中,∠D=90°,DG:GE=1:3,GE=GF,Q是EF上一动点,过点Q作QM⊥DE于M,QN⊥GF于N,,则QM+QN的长是 .
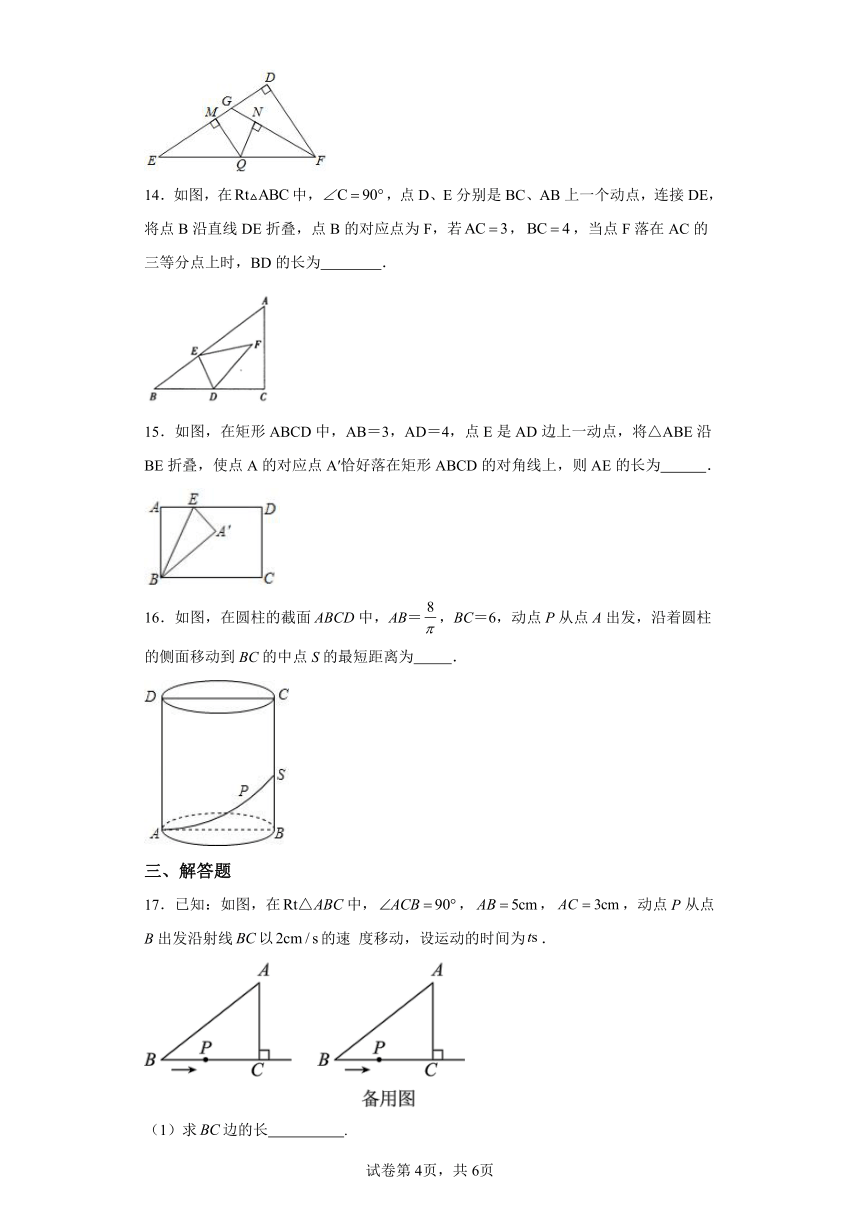
14.如图,在中,,点D、E分别是BC、AB上一个动点,连接DE,将点B沿直线DE折叠,点B的对应点为F,若,,当点F落在AC的三等分点上时,BD的长为 .
15.如图,在矩形ABCD中,AB=3,AD=4,点E是AD边上一动点,将△ABE沿BE折叠,使点A的对应点A′恰好落在矩形ABCD的对角线上,则AE的长为 .
16.如图,在圆柱的截面ABCD中,AB=,BC=6,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S的最短距离为 .
三、解答题
17.已知:如图,在中,,,,动点P从点B出发沿射线以的速 度移动,设运动的时间为.
(1)求边的长 .
(2)当为直角三角形时,t的值
18.已知中,,,,,是边上的两个动点,其中点从点开始沿方向运动且速度为每秒,点从点开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为秒.
(1)出发2秒后,求的长;
(2)当点在边上运动时,为何值时,的面积是的面积的.
19.已知:如图,在中,,,,动点从点出发沿射线以的速度移动,设运动的时间为秒.
(1)求边的长;
(2)当为直角三角形时,求t的值;
(3)当为等腰三角形时,求t的值.
20.如图,在中,,,,动点P从点B出发,沿射线BC以2cm/s的速度移动,设运动的时间为t(s).
(1)求BC边的长.
(2)当为直角三角形时,求t的值.
21.在△ABC中,,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为直角三角形时,求t的值.
22.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发,以2cm/秒的速度沿BC移动至点C,设运动时间为秒.
(1)求BC的长;
(2)在点P的运动过程中,是否存在某个时刻t,使得点P到边AB的距离与点P到点C的距离相等?若存在,求出t的值;若不存在,请说明理由.
23.探究题:如图,在等腰三角形ABC中,AB=AC,其底边长为8 cm,腰长为5 cm,一动点P在底边上从点B出发向点C以0.25 cm/s的速度移动,请你探究:当点P运动多长时间时,点P与顶点A的连线PA与腰垂直.
24.Rt△AB C中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).当t为何值时,△ABP为直角三角形?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据题意,求出AC的长,AP的长介于AC和AB的长度之间,据此即可选出正确答案.
【详解】解:∵AB=10,BC=8,
∴AC==6,
则6≤AP≤10,
∴AP长不可能是5,
故选:A.
【点睛】本题考查了勾股定理,求出AC的长是解题的关键.
2.D
【分析】当MN⊥BC时最短;当M在点A,N在点C时,MN最长,利用勾股定理计算即可;
【详解】解:当MN⊥BC时
MN最短=AB=AE+BE=4+5=9
当M在点A,N在点C时,
MN最长===15
∴9≤MN≤15
故答案选D
【点睛】本题考查了两条平行线之间的距离以及勾股定理,识别出MN最短情况和最长情况是解题的关键.
3.A
【分析】根据题意AB=AC,点D表示点K在BC中点,由△ABC的积是10求BC,则可求BC,利用勾股定求AC可.
【详解】由图象可知,点D左右对应图象呈现对称性,则AB=AC,点K位于BC中点时,AE为△ABC底边BC上高,AE最小=5.
∵△ABC的面积是10,
∴=10,
解得BC=4,
由勾股定理a=AB===7,
故选择:A.
【点睛】本题考查三角形的面积公式和勾股定理,解题的关键是掌握三角形的面积公式和勾股定理.
4.C
【分析】根据折叠可得,再利用勾股定理即可求解.
【详解】解:根据折叠可知, ,
在中,,,,
,
故选:C.
【点睛】本题考查了勾股定理及翻折的性质,熟练掌握勾股定理是解题的关键.
5.C
【分析】设,则,进而得出,再用勾股定理求出,进而用勾股定理建立方程求出,最后用三角形的面积建立方程求解,即可求出答案.
【详解】解:设,则,
,
在中,根据勾股定理得,,
在中,,
根据勾股定理得,,
,
(舍去)或,
,
连接,过点作于,如图所示:
,
,
在中,根据勾股定理得,,
,
,,
,故C正确.
故选:C.
【点睛】本题主要考查了勾股定理,三角形的面积公式,作出辅助线构造出直角三角形是解本题的关键.
6.C
【分析】勾股定理求得的长,进而根据三角形周长公式求解,根据进行线段的转化即可
【详解】解:在中,,,,
的周长为
故选C
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
7.D
【分析】首先过C作CE⊥AB,当D与E重合时,CE最短,首先利用三角形面积求得CE的长,然后可得CD的取值范围,进而可得答案.
【详解】解:过C作CE⊥AB,
∵AB=AC=15,且△ABC的面积为90,
∴S△ABC==90,
∴CE=12,
∴AE==9,
∴BE=15﹣9=6,
∴CB=,
∵D是线段AB上的动点(含端点A、B).
∴12≤CD≤15,
∴CD=12或13或14或15,
∵线段CD长为正整数,
∴CD的可以有5条,长为15,14,13,12,13
∴点D的个数共有5个,
故选D.
【点睛】本题考查勾股定理和三角形面积公式,解题的关键是掌握勾股定理和三角形面积公式.
8.C
【分析】作点P关于的对称点D,E,连接,如图,利用轴对称的性质证明,,的周长,即可解决问题.
【详解】解:作点P关于的对称点D,E,连接,如图,
则垂直平分,垂直平分,
∴,
∴,,
∴,
∴的周长(当D、M、N、E四点共线时取等号),
∴的周长的最小值即为的长,
∵,
∴的周长的最小值是;
故选:C.
【点睛】本题考查了对称轴的性质、勾股定理等知识,正确添加辅助线、得出的周长的最小值即为的长是解题的关键.
9.
【分析】延长,过点作的垂线,垂足为点,根据和的面积相等可知线段AD是中线,,根据直角三角形的勾股定理可得的长度.
【详解】解:延长,过点作的垂线,垂足为点,如图所示
∵和的面积相等
∴
∵
∴
∵根据三角形中线的性质可知
∴
∵
∴
∴在中可得
在中可得
∴
∴在中可得
故答案为:
【点睛】本题考查了三角形的中线和面积的关系以及勾股定理等知识点,灵活运用三角形的中线和面积的关系是解题的关键.
10.
【分析】假设为直角三角形,可得,设,则,,根据勾股定理即可求解.
【详解】解:如图所示,
与关于直线对称,,,当为直角三角形时,
∵,
∴点,,在同一条直线上,则有,,
∴设,则,,
∴,则,
∴,即,解方程得,,
故答案为:.
【点睛】本题主要考查长方形的性质与直角三角形的勾股定理得综合,掌握长方形的性质,勾股定理是解题的关键.
11.或
【分析】若,分两种情况讨论:①当点P从点C出发,运动在上时,②当点P从点C出发运动到上时,利用勾股定理及三角形等面积法列出方程求解即可.
【详解】解:①当点P从点C出发,运动在上时,若,则
,即,
∴cm.
故由点P的运动速度为每秒2 cm,
∴秒
它从C点出发秒时,有;
②当点P从点C出发运动到上时,如图,可过点C作于E.
∵,,,
∴cm,
∴,
∴cm,
设点P运动时间为t秒,
∴,
若,
则,即,
解得秒,
综上可得:从点C出发秒或秒时,,
故答案为:或.
【点睛】本题主要考查了勾股定理和三角形的面积的计算方法,理解题意,进行分类讨论是解题关键.
12.13
【分析】作点N关于AC的对称点D,连接CD,MD,BD,可得BM+MN=BM+MD≥BD,∠BCD=90°,从而得到BM+MN的最小值为BD的长,再由勾股定理,即可求解.
【详解】解:如图,作点N关于AC的对称点D,连接CD,MD,BD,
∴MD=MN,CN=CD,∠DCM=∠ACB=45°,
∴BM+MN=BM+MD≥BD,∠BCD=90°,
∴BM+MN的最小值为BD的长,
∵BC=12,BN=7,
∴CN=CD=5,
∴.
故答案为:13
【点睛】本题主要考查了轴对称的性质,勾股定理,熟练掌握轴对称的性质,勾股定理是解题的关键.
13.4
【分析】连接解直角三角形求出,再证明,即可解决问题.
【详解】解:连接.
,
可以假设,,
,,
,,
,,
,
或(舍弃),
,
,
,
故答案为:4.
【点睛】本题考查解直角三角形,勾股定理,等腰三角形的性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
14.或
【分析】点F落在的三等分点上得或,在中,根据勾股定理,分类讨论,求出BD即可.
【详解】由折叠性质可知,
∵点F落在的三等分点上,
∴或,
若时,在中,,
∴,
∴;
当时,在中,,
∴,
∴.
综上所述,的长为或.
【点睛】本题考查折叠问题,掌握折叠图形的性质,会利用三等分点的位置进行分类计算,会利用折叠转化等量关系,利用直角三角形构造方程解决问题是关键.
15.
【分析】由勾股定理可求BD长,由折叠的性质可得AB=A'B=3,∠A=∠BA'E=90°,AE=A'E,由勾股定理列出方程,可求AE的长.
【详解】如图,
∵AB=3,AD=4,∠A=90°,
∴BD===5,
∵将△ABE沿BE折叠,
∴AB=A'B=3,∠A=∠BA'E=90°,AE=A'E,
∴A'D=BD﹣A'B=2,
∵DE2=A'E2+A'D2,
∴(4﹣AE)2=AE2+4,
∴AE=,
故答案为:
【点睛】本题考查勾股定理和折叠的性质,解题的关键是掌握勾股定理和折叠的性质.
16.5
【分析】先把圆柱的侧面展开,连接AS,利用勾股定理即可得出AS的长.
【详解】如图所示,
∵在圆柱的截面ABCD中AB=,BC=6,
∴AB=××π=4,BS=BC=3,
∴AS==5.
故答案为:5.
【点睛】本题考查勾股定理,解题的关键是掌握勾股定理的应用.
17. 2或
【分析】(1)利用勾股定理求解即可得;
(2)先求出,再分①当,②当两种情况,利用勾股定理求解即可得.
【详解】解:(1)在中,,,,
由勾股定理得;
(2)由题意知:.
①当时,如图,点与点重合,,
;
②当时,如图2,,.
在中,,
在中,,
因此,
解得.
综上所述,当为直角三角形时,的值为2或.
【点睛】本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.
18.(1)
(2)
【分析】(1)求出,利用勾股定理求出的长;
(2)先求出,根据的面积是面积的得,计算即可;
【详解】(1)解:当出发2秒后,,
∴,
∵,
∴
(2)解:∵,
∴,
∴,
得.
【点睛】此题考查了勾股定理,三角形与动点问题,实际问题与一元一次方程,列比例求解,解题中运用分类思想,正确掌握勾股定理的计算公式是解题的关键.
19.(1)3cm
(2)3或
(3)5或6或
【分析】(1)利用勾股定理即可求出结论;
(2)由题意可得:,,然后根据直角三角形直角的情况分类讨论,利用勾股定理等知识即可解答;
(3)当为等腰三角形,根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据三线合一、勾股定理等知识即可解答.
【详解】(1)解:∵在中,,,,
∴.
(2)解:
当时,点与点重合,
∴,
即;
当时,如下图所示:
∴.
∵,
∴,
解得:.
综上:当为直角三角形时,或;
(3)解:当时,如下图所示:
∵,
∴,
即.
当时,如下图所示:
∴;
当时,如下图所示:
则,,
在中,,
即,
解得: .
综上:当为轴对称图形时,或或.
【点睛】此题考查的是勾股定理、等腰三角形的性质,掌握勾股定理、等腰三角形的性质是解决此题的关键.
20.(1)
(2)t的值为4或
【分析】(1)利用勾股定理求解即可得;
(2)先求出BP=2tcm,再分①当,②当两种情况,利用勾股定理求解即可得.
【详解】(1)在中,
由勾股定理得,
∴.
(2)由题意知.
①当时,如图1,点P与点C重合,,
∴.
②当时,如图2,,.
在中,,
在中,,
因此,
解得.
综上所述,当为直角三角形时,t的值为4或.
图1 图2
【点睛】本题考查了勾股定理,较难的是题(2),正确分两种情况讨论是解题关键.
21.当△ABP为直角三角形时,t=4或.
【分析】当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时t的值即可.
【详解】在Rt△ABC中,由勾股定理得:,
∴BC=4cm,
由题意得:BP=tcm.,
①当∠APB为直角时,
如图①,点P与点C重合,
BP=BC=4cm,
∴t=4;
②当∠BAP为直角时,
如图②,BP=tcm.CP=(t-4)cm,AC=3cm,
在Rt△ACP中,,
在Rt△BAP中,,
即,
解得,
答:当△ABP为直角三角形时,t=4或.
【点睛】本题考查了勾股定理以及直角三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分类讨论,否则会出现漏解.
22.(1)
(2)
【分析】(1)直接利用勾股定理求解即可;
(2)如图所示,过点P作PD⊥AB于D,由题意得,则,证明Rt△ADP≌Rt△ACP从而求出,
在Rt△PBD中由,得到,由此求解即可.
【详解】(1)解:∵在△ABC中,∠C=90°,AB=10cm,AC=6cm,
∴;
(2)解:如图所示,过点P作PD⊥AB于D,
由题意得,则,
在Rt△ADP和Rt△ACP中,
,
∴Rt△ADP≌Rt△ACP(HL),
∴,
∴,
在Rt△PBD中,,
∴,
解得.
【点睛】本题主要考查了全等三角形的性质与判定,勾股定理,正确作出辅助线,构造全等三角形是解题的关键.
23.当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【分析】利用勾股定理求出AD的长,再利用勾股定理逆定理即可证明垂直.
【详解】(1)过点A作AD⊥BC于点D.
∵AB=AC,BC=8 cm,
∴BD=CD=BC=4 cm.
由勾股定理,得AD==3(cm).
分两种情况:(1)如图,当点P运动t秒后有PA⊥AC(P在线段BD上)时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,
∴BP=4-2.25=1.75,
∴0.25t=1.75,解得t=7.
(2)当点P运动t秒后有PA⊥AB(P在线段CD上)时,同理可得PD=2.25,∴BP=4+2.25=6.25,
∴0.25t=6.25,解得t=25.
综上所述,当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【点睛】本题考查了勾股定理与勾股定理逆定理的应用,熟悉概念是解题关键.
24.4或12.5
【分析】分当∠AP1B=90°,△ABP1为直角三角形时和当∠BAP2=90°,△ABP2为直角三角形时两种情况讨论即可.
【详解】解:在Rt△ABC中,由勾股定理得:
BC2+AC2=AB2
∴BC2+62=102
∴BC=8,
当∠AP1B=90°,△ABP1为直角三角形时,P1在C处,即BP1=8,
∴8÷2=4(s);
当∠BAP2=90°,△ABP2为直角三角形时,
设BP2为x,则CP2=x-8
在△ACP2中,由勾股定理得:
AC2+CP22=AP22
∴62+(x-8)2=AP22
在△BAP2中,由勾股定理得:
AB2+AP22=BP22
∴AP22= BP22- AB2=x2-102
∴x2-102=62+(x-8)2
∴x=12.5.
【点睛】本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用.
答案第1页,共2页
答案第1页,共2页
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习.
一、单选题
1.如图,在△ABC中,∠C=90°,AB=10,BC=8,点P是边BC上的动点,则AP的长不可能为( )
A.5 B.6 C.7 D.9
2.已知Rt△BCE和Rt△ADE按如图方式摆放,∠A=∠B=90°,A、E、B在一条直线上,AD=3,AE=4,EB=5,BC=12,M是线段AD上的动点,N是线段BC上的动点,MN的长度不可能是( )
A.9 B.12 C.14 D.16
3.如图1,动点K从△ABC的顶点A出发,沿AB→BC匀速运动到点C停止,在动点K运动过程中,线段AK的长y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,若△ABC的面积是10 ,则a为( )
A.7 B.2 C.4 D.2
4.如图,在中,,,,点F在AC上,并且,点E为上的动点(点E不与点C重合),将沿直线翻折,使点C落在点P处,的长为,则边的长为( )
A. B.3 C. D.4
5.如图,在中,,,,Q是上一动点,过点Q作于M,于N,,则的长是( )
A. B. C.4 D.
6.如图,在中,,,,D为AB上一动点,当时,的周长为( )
A.14 B.15 C.16 D.18
7.如图,在△ABC中,AB=AC=15,且△ABC的面积为90,D是线段AB上的动点(包含端点),若线段CD的长为正整数,则点D的个数共有( )
A.2个 B.3个 C.4个 D.5个
8.如图,,内有一点P,,M是上一动点,N是上一动点,则周长的最小值为( )
A.6 B.3 C. D.
二、填空题
9.如图,在中,,点是边上一动点,交于点,当时,的面积恰好等于的面积,连接,则此时=
10.如图,长方形中,,.点为线段上的一个动点,与关于直线对称,当为直角三角形时,为
11.在中,,,,动点P从C出发,以每秒2cm的速度沿着运动到点B,则从点C出发 秒时,可使.
12.如图,在锐角△ABC中,∠ACB=45°,BC=12,点N为BC上一点,且BN=7,点M 为线段AC上一动点,连接BM、MN,则BM+MN的最小值为 .
13.如图,在△DEF中,∠D=90°,DG:GE=1:3,GE=GF,Q是EF上一动点,过点Q作QM⊥DE于M,QN⊥GF于N,,则QM+QN的长是 .
14.如图,在中,,点D、E分别是BC、AB上一个动点,连接DE,将点B沿直线DE折叠,点B的对应点为F,若,,当点F落在AC的三等分点上时,BD的长为 .
15.如图,在矩形ABCD中,AB=3,AD=4,点E是AD边上一动点,将△ABE沿BE折叠,使点A的对应点A′恰好落在矩形ABCD的对角线上,则AE的长为 .
16.如图,在圆柱的截面ABCD中,AB=,BC=6,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S的最短距离为 .
三、解答题
17.已知:如图,在中,,,,动点P从点B出发沿射线以的速 度移动,设运动的时间为.
(1)求边的长 .
(2)当为直角三角形时,t的值
18.已知中,,,,,是边上的两个动点,其中点从点开始沿方向运动且速度为每秒,点从点开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为秒.
(1)出发2秒后,求的长;
(2)当点在边上运动时,为何值时,的面积是的面积的.
19.已知:如图,在中,,,,动点从点出发沿射线以的速度移动,设运动的时间为秒.
(1)求边的长;
(2)当为直角三角形时,求t的值;
(3)当为等腰三角形时,求t的值.
20.如图,在中,,,,动点P从点B出发,沿射线BC以2cm/s的速度移动,设运动的时间为t(s).
(1)求BC边的长.
(2)当为直角三角形时,求t的值.
21.在△ABC中,,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为直角三角形时,求t的值.
22.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发,以2cm/秒的速度沿BC移动至点C,设运动时间为秒.
(1)求BC的长;
(2)在点P的运动过程中,是否存在某个时刻t,使得点P到边AB的距离与点P到点C的距离相等?若存在,求出t的值;若不存在,请说明理由.
23.探究题:如图,在等腰三角形ABC中,AB=AC,其底边长为8 cm,腰长为5 cm,一动点P在底边上从点B出发向点C以0.25 cm/s的速度移动,请你探究:当点P运动多长时间时,点P与顶点A的连线PA与腰垂直.
24.Rt△AB C中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).当t为何值时,△ABP为直角三角形?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据题意,求出AC的长,AP的长介于AC和AB的长度之间,据此即可选出正确答案.
【详解】解:∵AB=10,BC=8,
∴AC==6,
则6≤AP≤10,
∴AP长不可能是5,
故选:A.
【点睛】本题考查了勾股定理,求出AC的长是解题的关键.
2.D
【分析】当MN⊥BC时最短;当M在点A,N在点C时,MN最长,利用勾股定理计算即可;
【详解】解:当MN⊥BC时
MN最短=AB=AE+BE=4+5=9
当M在点A,N在点C时,
MN最长===15
∴9≤MN≤15
故答案选D
【点睛】本题考查了两条平行线之间的距离以及勾股定理,识别出MN最短情况和最长情况是解题的关键.
3.A
【分析】根据题意AB=AC,点D表示点K在BC中点,由△ABC的积是10求BC,则可求BC,利用勾股定求AC可.
【详解】由图象可知,点D左右对应图象呈现对称性,则AB=AC,点K位于BC中点时,AE为△ABC底边BC上高,AE最小=5.
∵△ABC的面积是10,
∴=10,
解得BC=4,
由勾股定理a=AB===7,
故选择:A.
【点睛】本题考查三角形的面积公式和勾股定理,解题的关键是掌握三角形的面积公式和勾股定理.
4.C
【分析】根据折叠可得,再利用勾股定理即可求解.
【详解】解:根据折叠可知, ,
在中,,,,
,
故选:C.
【点睛】本题考查了勾股定理及翻折的性质,熟练掌握勾股定理是解题的关键.
5.C
【分析】设,则,进而得出,再用勾股定理求出,进而用勾股定理建立方程求出,最后用三角形的面积建立方程求解,即可求出答案.
【详解】解:设,则,
,
在中,根据勾股定理得,,
在中,,
根据勾股定理得,,
,
(舍去)或,
,
连接,过点作于,如图所示:
,
,
在中,根据勾股定理得,,
,
,,
,故C正确.
故选:C.
【点睛】本题主要考查了勾股定理,三角形的面积公式,作出辅助线构造出直角三角形是解本题的关键.
6.C
【分析】勾股定理求得的长,进而根据三角形周长公式求解,根据进行线段的转化即可
【详解】解:在中,,,,
的周长为
故选C
【点睛】本题考查了勾股定理,掌握勾股定理是解题的关键.
7.D
【分析】首先过C作CE⊥AB,当D与E重合时,CE最短,首先利用三角形面积求得CE的长,然后可得CD的取值范围,进而可得答案.
【详解】解:过C作CE⊥AB,
∵AB=AC=15,且△ABC的面积为90,
∴S△ABC==90,
∴CE=12,
∴AE==9,
∴BE=15﹣9=6,
∴CB=,
∵D是线段AB上的动点(含端点A、B).
∴12≤CD≤15,
∴CD=12或13或14或15,
∵线段CD长为正整数,
∴CD的可以有5条,长为15,14,13,12,13
∴点D的个数共有5个,
故选D.
【点睛】本题考查勾股定理和三角形面积公式,解题的关键是掌握勾股定理和三角形面积公式.
8.C
【分析】作点P关于的对称点D,E,连接,如图,利用轴对称的性质证明,,的周长,即可解决问题.
【详解】解:作点P关于的对称点D,E,连接,如图,
则垂直平分,垂直平分,
∴,
∴,,
∴,
∴的周长(当D、M、N、E四点共线时取等号),
∴的周长的最小值即为的长,
∵,
∴的周长的最小值是;
故选:C.
【点睛】本题考查了对称轴的性质、勾股定理等知识,正确添加辅助线、得出的周长的最小值即为的长是解题的关键.
9.
【分析】延长,过点作的垂线,垂足为点,根据和的面积相等可知线段AD是中线,,根据直角三角形的勾股定理可得的长度.
【详解】解:延长,过点作的垂线,垂足为点,如图所示
∵和的面积相等
∴
∵
∴
∵根据三角形中线的性质可知
∴
∵
∴
∴在中可得
在中可得
∴
∴在中可得
故答案为:
【点睛】本题考查了三角形的中线和面积的关系以及勾股定理等知识点,灵活运用三角形的中线和面积的关系是解题的关键.
10.
【分析】假设为直角三角形,可得,设,则,,根据勾股定理即可求解.
【详解】解:如图所示,
与关于直线对称,,,当为直角三角形时,
∵,
∴点,,在同一条直线上,则有,,
∴设,则,,
∴,则,
∴,即,解方程得,,
故答案为:.
【点睛】本题主要考查长方形的性质与直角三角形的勾股定理得综合,掌握长方形的性质,勾股定理是解题的关键.
11.或
【分析】若,分两种情况讨论:①当点P从点C出发,运动在上时,②当点P从点C出发运动到上时,利用勾股定理及三角形等面积法列出方程求解即可.
【详解】解:①当点P从点C出发,运动在上时,若,则
,即,
∴cm.
故由点P的运动速度为每秒2 cm,
∴秒
它从C点出发秒时,有;
②当点P从点C出发运动到上时,如图,可过点C作于E.
∵,,,
∴cm,
∴,
∴cm,
设点P运动时间为t秒,
∴,
若,
则,即,
解得秒,
综上可得:从点C出发秒或秒时,,
故答案为:或.
【点睛】本题主要考查了勾股定理和三角形的面积的计算方法,理解题意,进行分类讨论是解题关键.
12.13
【分析】作点N关于AC的对称点D,连接CD,MD,BD,可得BM+MN=BM+MD≥BD,∠BCD=90°,从而得到BM+MN的最小值为BD的长,再由勾股定理,即可求解.
【详解】解:如图,作点N关于AC的对称点D,连接CD,MD,BD,
∴MD=MN,CN=CD,∠DCM=∠ACB=45°,
∴BM+MN=BM+MD≥BD,∠BCD=90°,
∴BM+MN的最小值为BD的长,
∵BC=12,BN=7,
∴CN=CD=5,
∴.
故答案为:13
【点睛】本题主要考查了轴对称的性质,勾股定理,熟练掌握轴对称的性质,勾股定理是解题的关键.
13.4
【分析】连接解直角三角形求出,再证明,即可解决问题.
【详解】解:连接.
,
可以假设,,
,,
,,
,,
,
或(舍弃),
,
,
,
故答案为:4.
【点睛】本题考查解直角三角形,勾股定理,等腰三角形的性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
14.或
【分析】点F落在的三等分点上得或,在中,根据勾股定理,分类讨论,求出BD即可.
【详解】由折叠性质可知,
∵点F落在的三等分点上,
∴或,
若时,在中,,
∴,
∴;
当时,在中,,
∴,
∴.
综上所述,的长为或.
【点睛】本题考查折叠问题,掌握折叠图形的性质,会利用三等分点的位置进行分类计算,会利用折叠转化等量关系,利用直角三角形构造方程解决问题是关键.
15.
【分析】由勾股定理可求BD长,由折叠的性质可得AB=A'B=3,∠A=∠BA'E=90°,AE=A'E,由勾股定理列出方程,可求AE的长.
【详解】如图,
∵AB=3,AD=4,∠A=90°,
∴BD===5,
∵将△ABE沿BE折叠,
∴AB=A'B=3,∠A=∠BA'E=90°,AE=A'E,
∴A'D=BD﹣A'B=2,
∵DE2=A'E2+A'D2,
∴(4﹣AE)2=AE2+4,
∴AE=,
故答案为:
【点睛】本题考查勾股定理和折叠的性质,解题的关键是掌握勾股定理和折叠的性质.
16.5
【分析】先把圆柱的侧面展开,连接AS,利用勾股定理即可得出AS的长.
【详解】如图所示,
∵在圆柱的截面ABCD中AB=,BC=6,
∴AB=××π=4,BS=BC=3,
∴AS==5.
故答案为:5.
【点睛】本题考查勾股定理,解题的关键是掌握勾股定理的应用.
17. 2或
【分析】(1)利用勾股定理求解即可得;
(2)先求出,再分①当,②当两种情况,利用勾股定理求解即可得.
【详解】解:(1)在中,,,,
由勾股定理得;
(2)由题意知:.
①当时,如图,点与点重合,,
;
②当时,如图2,,.
在中,,
在中,,
因此,
解得.
综上所述,当为直角三角形时,的值为2或.
【点睛】本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.
18.(1)
(2)
【分析】(1)求出,利用勾股定理求出的长;
(2)先求出,根据的面积是面积的得,计算即可;
【详解】(1)解:当出发2秒后,,
∴,
∵,
∴
(2)解:∵,
∴,
∴,
得.
【点睛】此题考查了勾股定理,三角形与动点问题,实际问题与一元一次方程,列比例求解,解题中运用分类思想,正确掌握勾股定理的计算公式是解题的关键.
19.(1)3cm
(2)3或
(3)5或6或
【分析】(1)利用勾股定理即可求出结论;
(2)由题意可得:,,然后根据直角三角形直角的情况分类讨论,利用勾股定理等知识即可解答;
(3)当为等腰三角形,根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据三线合一、勾股定理等知识即可解答.
【详解】(1)解:∵在中,,,,
∴.
(2)解:
当时,点与点重合,
∴,
即;
当时,如下图所示:
∴.
∵,
∴,
解得:.
综上:当为直角三角形时,或;
(3)解:当时,如下图所示:
∵,
∴,
即.
当时,如下图所示:
∴;
当时,如下图所示:
则,,
在中,,
即,
解得: .
综上:当为轴对称图形时,或或.
【点睛】此题考查的是勾股定理、等腰三角形的性质,掌握勾股定理、等腰三角形的性质是解决此题的关键.
20.(1)
(2)t的值为4或
【分析】(1)利用勾股定理求解即可得;
(2)先求出BP=2tcm,再分①当,②当两种情况,利用勾股定理求解即可得.
【详解】(1)在中,
由勾股定理得,
∴.
(2)由题意知.
①当时,如图1,点P与点C重合,,
∴.
②当时,如图2,,.
在中,,
在中,,
因此,
解得.
综上所述,当为直角三角形时,t的值为4或.
图1 图2
【点睛】本题考查了勾股定理,较难的是题(2),正确分两种情况讨论是解题关键.
21.当△ABP为直角三角形时,t=4或.
【分析】当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时t的值即可.
【详解】在Rt△ABC中,由勾股定理得:,
∴BC=4cm,
由题意得:BP=tcm.,
①当∠APB为直角时,
如图①,点P与点C重合,
BP=BC=4cm,
∴t=4;
②当∠BAP为直角时,
如图②,BP=tcm.CP=(t-4)cm,AC=3cm,
在Rt△ACP中,,
在Rt△BAP中,,
即,
解得,
答:当△ABP为直角三角形时,t=4或.
【点睛】本题考查了勾股定理以及直角三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分类讨论,否则会出现漏解.
22.(1)
(2)
【分析】(1)直接利用勾股定理求解即可;
(2)如图所示,过点P作PD⊥AB于D,由题意得,则,证明Rt△ADP≌Rt△ACP从而求出,
在Rt△PBD中由,得到,由此求解即可.
【详解】(1)解:∵在△ABC中,∠C=90°,AB=10cm,AC=6cm,
∴;
(2)解:如图所示,过点P作PD⊥AB于D,
由题意得,则,
在Rt△ADP和Rt△ACP中,
,
∴Rt△ADP≌Rt△ACP(HL),
∴,
∴,
在Rt△PBD中,,
∴,
解得.
【点睛】本题主要考查了全等三角形的性质与判定,勾股定理,正确作出辅助线,构造全等三角形是解题的关键.
23.当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【分析】利用勾股定理求出AD的长,再利用勾股定理逆定理即可证明垂直.
【详解】(1)过点A作AD⊥BC于点D.
∵AB=AC,BC=8 cm,
∴BD=CD=BC=4 cm.
由勾股定理,得AD==3(cm).
分两种情况:(1)如图,当点P运动t秒后有PA⊥AC(P在线段BD上)时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,
∴BP=4-2.25=1.75,
∴0.25t=1.75,解得t=7.
(2)当点P运动t秒后有PA⊥AB(P在线段CD上)时,同理可得PD=2.25,∴BP=4+2.25=6.25,
∴0.25t=6.25,解得t=25.
综上所述,当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【点睛】本题考查了勾股定理与勾股定理逆定理的应用,熟悉概念是解题关键.
24.4或12.5
【分析】分当∠AP1B=90°,△ABP1为直角三角形时和当∠BAP2=90°,△ABP2为直角三角形时两种情况讨论即可.
【详解】解:在Rt△ABC中,由勾股定理得:
BC2+AC2=AB2
∴BC2+62=102
∴BC=8,
当∠AP1B=90°,△ABP1为直角三角形时,P1在C处,即BP1=8,
∴8÷2=4(s);
当∠BAP2=90°,△ABP2为直角三角形时,
设BP2为x,则CP2=x-8
在△ACP2中,由勾股定理得:
AC2+CP22=AP22
∴62+(x-8)2=AP22
在△BAP2中,由勾股定理得:
AB2+AP22=BP22
∴AP22= BP22- AB2=x2-102
∴x2-102=62+(x-8)2
∴x=12.5.
【点睛】本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
