专题1.31勾股定理全章复习与巩固 中考真题专练(含解析)2023-2024学年八年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.31勾股定理全章复习与巩固 中考真题专练(含解析)2023-2024学年八年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 894.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览



文档简介
专题1.31 勾股定理全章复习与巩固(中考真题专练)
一、单选题
(2023·湖北·统考中考真题)
1.如图,在中,,点在边上,且平分的周长,则的长是( )
A. B. C. D.
(2023·四川泸州·统考中考真题)
2.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数,,的计算公式:,,,其中,,是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )
A.3,4,5 B.5,12,13 C.6,8,10 D.7,24,25
(2022·广西桂林·统考中考真题)
3.如图,在ABC中,∠B=22.5°,∠C=45°,若AC=2,则ABC的面积是( )
A. B.1+ C.2 D.2+
(2021·山东滨州·统考中考真题)
4.在中,若,,,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
(2021·四川凉山·统考中考真题)
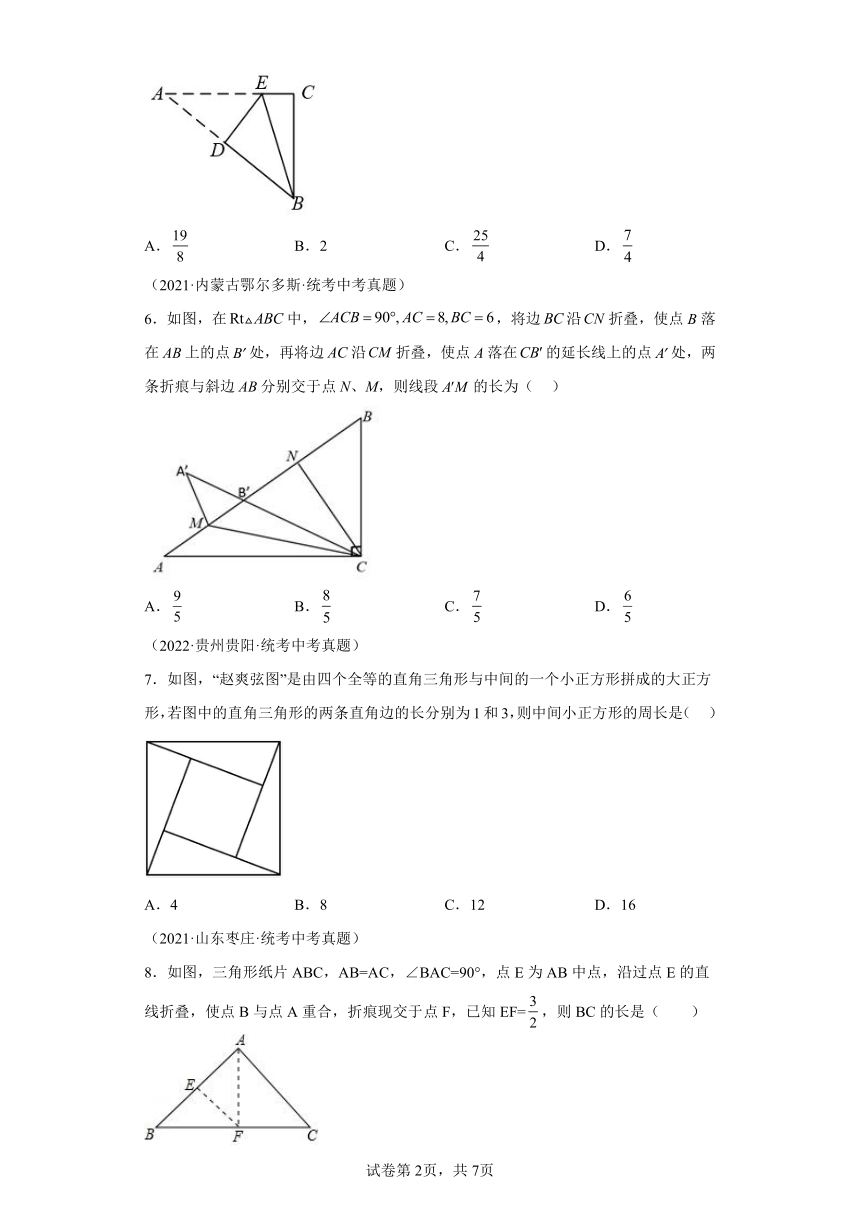
5.如图,中,,将沿DE翻折,使点A与点B重合,则CE的长为( )
A. B.2 C. D.
(2021·内蒙古鄂尔多斯·统考中考真题)
6.如图,在中,,将边沿折叠,使点B落在上的点处,再将边沿折叠,使点A落在的延长线上的点处,两条折痕与斜边分别交于点N、M,则线段的长为( )
A. B. C. D.
(2022·贵州贵阳·统考中考真题)
7.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
(2021·山东枣庄·统考中考真题)
8.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=,则BC的长是( )
A. B.3 C.3 D.3
二、填空题
(2023·湖北随州·统考中考真题)
9.如图,在中,,D为AC上一点,若是的角平分线,则 .
(2023·山东东营·统考中考真题)
10.一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km至C港,则A,C两港之间的距离为 km.
(2022·内蒙古鄂尔多斯·统考中考真题)
11.如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE=,则AB的长是 .
(2023·四川广安·统考中考真题)
12.如图,圆柱形玻璃杯的杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为 .(杯壁厚度不计)
(2022·黑龙江牡丹江·统考中考真题)
13.在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD= .
(2022·辽宁朝阳·统考中考真题)
14.如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是 .
(2022·湖北黄冈·统考中考真题)
15.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
(2021·江苏宿迁·统考中考真题)
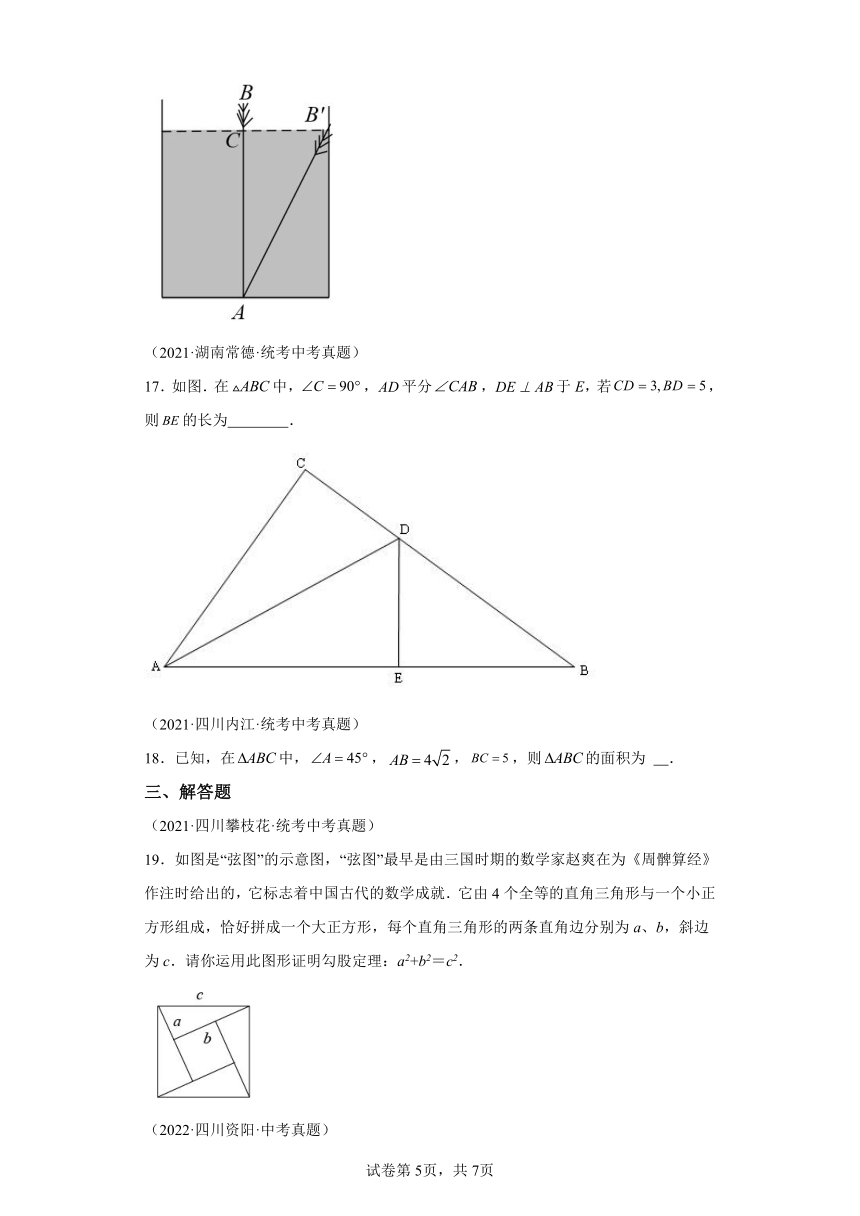
16.《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇生长在它的中央,高出水面部分为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的(示意图如图,则水深为 尺.
(2021·湖南常德·统考中考真题)
17.如图.在中,,平分,于E,若,则的长为 .
(2021·四川内江·统考中考真题)
18.已知,在中,,,,则的面积为 .
三、解答题
(2021·四川攀枝花·统考中考真题)
19.如图是“弦图”的示意图,“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,它标志着中国古代的数学成就.它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,每个直角三角形的两条直角边分别为a、b,斜边为c.请你运用此图形证明勾股定理:a2+b2=c2.
(2022·四川资阳·中考真题)
20.如图,在中,过点C作,在上截取,上截取,连接.
(1)求证:;
(2)若,求的面积.
(2021·湖南长沙·统考中考真题)
21.如图,在中,,垂足为,,延长至,使得,连接.
(1)求证:;
(2)若,,求的周长和面积.
(2020·浙江温州·统考中考真题)
22.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
(2018·甘肃天水·中考真题)
23.如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=,BE=.求CD的长和四边形ABCD的面积.
(2013·吉林·中考真题)
24.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3cm,则BE= cm.
(2019·河北·统考中考真题)
25.已知:整式,整式.
尝试: 化简整式.
发现: ,求整式.
联想:由上可知,,当n>1时为直角三角形的三边长,如图.填写下表中的值:
直角三角形三边
勾股数组Ⅰ / 8
勾股数组Ⅱ /
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】如图所示,过点B作于E,利用勾股定理求出,进而利用等面积法求出,则可求出,再由平分的周长,求出,进而得到,则由勾股定理得.
【详解】解:如图所示,过点B作于E,
∵在中,,
∴,
∵,
∴,
∴,
∵平分的周长,
∴,即,
又∵,
∴,
∴,
∴,
故选C.
【点睛】本题主要考查了勾股定理,正确作出辅助线构造直角三角形是解题的关键.
2.C
【分析】首先证明出,得到a,b是直角三角形的直角边然后由,,是互质的奇数逐项求解即可.
【详解】∵,
∴.
∵,
∴.
∴a,b是直角三角形的直角边,
∵,是互质的奇数,
∴A.,
∴当,时,,,,
∴3,4,5能由该勾股数计算公式直接得出;
B.,
∴当,时,,,,
∴5,12,13能由该勾股数计算公式直接得出;
C.,,
∵,是互质的奇数,
∴6,8,10不能由该勾股数计算公式直接得出;
D.,
∴当,时,,,,
∴7,24,25能由该勾股数计算公式直接得出.
故选:C.
【点睛】本题考查了勾股数的应用,通过,,是互质的奇数这两个条件去求得符合题意的t的值是解决本题的关键.
3.D
【分析】如图,过点A作AD⊥AC于A,交BC于D,过点A作AE⊥BC于E,先证明△ADC是等腰直角三角形,得AD=AC=2,∠ADC=45°,CD=AC=2,再证明AD=BD,计算AE和BC的长,根据三角形的面积公式可解答.
【详解】解:如图,过点A作AD⊥AC于A,交BC于D,过点A作AE⊥BC于E,
∵∠C=45°,
∴△ADC是等腰直角三角形,
∴AD=AC=2,∠ADC=45°,CD=AC=2,
∵∠ADC=∠B+∠BAD,∠B=22.5°,
∴∠DAB=22.5°,
∴∠B=∠DAB,
∴AD=BD=2,
∵AD=AC,AE⊥CD,
∴DE=CE,
∴
∴△ABC的面积.
故选:D.
【点睛】本题考查的是勾股定理,等腰直角三角形的性质,三角形的面积,熟知掌握等腰三角形的性质是解本题的关键.
4.D
【分析】根据题意画出图形,然后作CD⊥AB于点D,根据勾股定理可以求得AB的长,然后根据面积法,可以求得CD的长.
【详解】解:作CD⊥AB于点D,如右图所示,
∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵,
∴,
解得CD=2.4,
故选:D.
【点睛】本题考查勾股定理、三角形的面积,解答本题的关键是明确题意,画出相应的图形,利用勾股定理和面积法解答.
5.D
【分析】先在RtABC中利用勾股定理计算出AB=10,再利用折叠的性质得到AE=BE,AD=BD=5,设AE=x,则CE=AC-AE=8-x,BE=x,在Rt△BCE中根据勾股定理可得到x2=62+(8-x)2,解得x,可得CE.
【详解】解:∵∠ACB=90°,AC=8,BC=6,
∴AB==10,
∵△ADE沿DE翻折,使点A与点B重合,
∴AE=BE,AD=BD=AB=5,
设AE=x,则CE=AC-AE=8-x,BE=x,
在Rt△BCE中
∵BE2=BC2+CE2,
∴x2=62+(8-x)2,解得x=,
∴CE==,
故选:D.
【点睛】本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理.
6.B
【分析】利用勾股定理求出AB=10,利用等积法求出CN=,从而得AN=,再证明∠NMC=∠NCM=45°,进而即可得到答案.
【详解】解:∵
∴AB=,
∵S△ABC=×AB×CN=×AC×BC
∴CN=,
∵AN=,
∵折叠
∴AM=A'M,∠BCN=∠B'CN,∠ACM=∠A'CM,
∵∠BCN+∠B'CN+∠ACM+∠A'CM=90°,
∴∠B'CN +∠A'CM=45°,
∴∠MCN=45°,且CN⊥AB,
∴∠NMC=∠NCM=45°,
∴MN=CN=,
∴A'M=AM=AN MN=-=.
故选B.
【点睛】本题考查了翻折变换,勾股定理,等腰直角三角形的性质,熟练运用折叠的性质是本题的关键.
7.B
【分析】根据图形分析可得小正方形的边长为两条直角边长的差,据此即可求解.
【详解】图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是.
故选B.
【点睛】本题考查了以弦图为背景的计算题,理解题意是解题的关键.
8.B
【分析】折叠的性质主要有:1.重叠部分全等;2.折痕是对称轴,对称点的连线被对称轴垂直平分. 由折叠的性质可知,所以可求出∠AFB=90°,再直角三角形的性质可知,所以,的长可求,再利用勾股定理即可求出BC的长.
【详解】解:
AB=AC,
,
故选B.
【点睛】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用,求出∠AFB=90°是解题的关键.
9.5
【分析】首先证明,,设,在中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
故答案为:5.
【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
10.50
【分析】根据题意画出图形,易证是直角三角形,利用勾股定理即可求解.
【详解】如图,根据题意,得,,,,
∵
∴
∴
∴在中,
即A,C两港之间的距离为50 km.
故答案为:50
【点睛】本题考查方位角,勾股定理,根据题意画出图形,证明是直角三角形是解题的关键.
11.12
【分析】延长BE交AD于点F,由“ASA”可证△BCE≌△FDE,可得DF=BC=5,BE=EF,由勾股定理可求AB的长.
【详解】如图,延长BE交AD于点F,
∵点E是DC的中点,
∴DE=CE,
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠ D=∠BCE,∠FED=∠BEC,
∴ △BCE≌△FDE(ASA),
∴DF=BC=5,BE=EF,
∴BF=2BE=13,AF=5,
在Rt△ABF中,由勾股定理可得AB=12.
故答案为:12.
【点睛】本题考查了全等三角形的判定和性质,勾股定理,添加恰当辅助线构造全等三角形是本题的关键.
12.10
【分析】如图(见解析),将玻璃杯侧面展开,作关于的对称点,根据两点之间线段最短可知的长度即为所求,利用勾股定理求解即可得.
【详解】解:如图,将玻璃杯侧面展开,作关于的对称点,作,交延长线于点,连接,
由题意得:,
,
∵底面周长为,
,
,
由两点之间线段最短可知,蚂蚁从外壁处到内壁处所走的最短路程为,
故答案为:10.
【点睛】本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
13.3.
【详解】试题分析:如图,过点D作DE⊥AB于E,
∵∠C=90°,AC=6,BC=8,
∴AB=,
∵AD平分∠CAB,
∴CD=DE,
∴S△ABC=AC CD+AB DE=AC BC,
即×6 CD+×10 CD=×6×8,
解得CD=3.
考点:1.角平分线的性质,2.勾股定理
14.18
【分析】由题可知,EF为线段BC的垂直平分线,则CD=BD,由勾股定理可得AC5,则△ACD的周长为AC+AD+CD=AC+AD+BD=AC+AB,即可得出答案.
【详解】解:由题可知,EF为线段BC的垂直平分线,
∴CD=BD,
∵∠ACB=90°,AB=13,BC=12,
∴AC5,
∴△ACD的周长为AC+AD+CD=AC+AD+BD=AC+AB=5+13=18.
故答案为:18.
【点睛】本题考查尺规作图、线段垂直平分线的性质、勾股定理,熟练掌握线段垂直平分线的性质及勾股定理是详解本题的关键.
15.m2+1
【分析】2m为偶数,设其股是a,则弦为a+2,根据勾股定理列方程即可得到结论.
【详解】∵2m为偶数,
∴设其股是a,则弦为a+2,
根据勾股定理得,(2m)2+a2=(a+2)2,
解得a=m2-1,
∴弦长为m2+1,
故答案为:m2+1.
【点睛】本题考查了勾股数,勾股定理,熟练掌握勾股定理是解题的关键.
16.12
【分析】我们可以将其转化为数学几何图形,如图所示,根据题意,可知的长为10尺,则尺,设出尺,表示出水深,根据勾股定理建立方程,求出的方程的解即可得到芦苇的长和水深.
【详解】解:设芦苇长尺,则水深尺,
因为尺,所以尺,
在中,,
.解得,
即水深12尺,芦苇长13尺.
故答案为:12.
【点睛】此题考查勾股定理的实际应用,正确理解题意,构建直角三角形利用勾股定理解决问题是解题的关键.
17.
【分析】证明三角形全等,再利用勾股定理即可求出.
【详解】解:由题意:平分,于,
,,
又为公共边,
,
,
在中,,由勾股定理得:
,
故答案是:.
【点睛】本题考查了三角形全等及勾股定理,解题的关键是:通过全等找到边之间的关系,再利用勾股定理进行计算可得.
18.2或14#14或2
【分析】过点B作AC边的高BD,Rt△ABD中,∠A=45°,AB=4,得BD=AD=4,在Rt△BDC中,BC=4,得CD==5,①△ABC是钝角三角形时,②△ABC是锐角三角形时,分别求出AC的长,即可求解.
【详解】解:过点作边的高,
中,,,
,
在中,,
,
①是钝角三角形时,
,
;
②是锐角三角形时,
,
,
故答案为:2或14.
【点睛】本题考查了勾股定理,三角形面积求法,解题关键是分类讨论思想.
19.见解析
【分析】根据大正方形的面积=小正方形的面积+4个直角三角形的面积证明即可
【详解】解:由题意得大正方形面积,小正方形面积,
4个小直角三角形的面积,
∵大正方形的面积=小正方形的面积+4个直角三角形的面积,
∴.
【点睛】本题主要考查了勾股定理的证明,解题的关键在于能够根据题意知晓大正方形的面积=小正方形的面积+4个直角三角形的面积.
20.(1)证明见解析
(2)
【分析】(1)根据,可以得到,即可用SAS证明得出结论;
(2)根据全等三角形的性质,可以得到,设,则,因为在中,,而在中,,即可列出方程求出三角形的面积.
【详解】(1)证明:∵
∴
又∵
∴;
(2)由(1),
∴,
设,∵,则,
在中,,
在中,,
∴,
即,整理得:,
解得:(舍去),
∴,
∴,,
∴.
【点睛】本题考查了全等三角形的判定和性质,勾股定理的应用,解一元二次方程,用方程思想解决几何问题是本题的关键.
21.(1)证明见解析;(2)周长为,面积为22.
【分析】(1)先根据垂直的定义可得,再根据三角形全等的判定定理与性质即可得证;
(2)先根据全等三角形的性质可得,从而可得,再利用勾股定理可得,从而可得,然后利用勾股定理可得,最后利用三角形的周长公式和面积公式即可得.
【详解】(1)证明:,
,
在和中,,
,
;
(2),,
,
,
,
,
,
,
,
,
,
则的周长为,
的面积为.
【点睛】本题考查了三角形全等的判定定理与性质、勾股定理等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.
22.(1)见解析;(2)13
【分析】根据题意可知,本题考查平行的性质,全等三角形的判定和勾股定理,根据判定定理,运用两直线平行内错角相等再通过AAS以及勾股定理进行求解.
【详解】解:(1)∵
∴
在△ABC和△DCE中
∴△ABC≌△DCE
(2)由(1)可得BC=CE=5
在直角三角形ACE中
【点睛】本题考查平行的性质,全等三角形的判定和勾股定理,熟练掌握判定定理运用以及平行的性质是解决此类问题的关键.
23.CD=2;四边形ABCD的面积是
【分析】利用等腰直角三角形的性质得出EH=DH=1,进而得出再利用直角三角形中30°所对边等于斜边的一半得出CD的长,求出AC,AB的长即可得出四边形ABCD的面积.
【详解】解:如图,过点D作DH⊥AC,
∵∠CED=45°,DH⊥EC,DE=,∴EH=DH.
∵EH2+DH2=ED2,∴EH2=1.∴EH=DH=1.
又∵∠DCE=30°,∴CD=2,HC=.
∵∠AEB=45°,∠BAC=90°,BE=.∴AB=AE=2.
∴AC=2+1+=3+.
∴S四边形ABCD=×2×(3+)+×1×(3+)=.
24.(1)见解析(2)6
【详解】(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE.
∵∠ACB=90°,
∴∠ACB=∠DCE.
∴∠ACB+∠BCD=∠DCE+∠BCD.
∴∠ACD=∠BCE.
∵在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS).
(2)∵AC=BC=3,∠ACB=90°,
∴由勾股定理得:AB=3.
又∵DB=AB,
∴AD=2AB=6.
∵△ACD≌△BCE,
∴BE=AD=6,
故答案为:
25.尝试:;发现:;联想:17,37.
【分析】先根据完全平方公式和整式的混合运算法则求出A,进而求出B,再把n的值代入即可解答.
【详解】A=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2.
∵A=B2,B>0,∴B=n2+1,当2n=8时,n=4,∴n2+1=42+1=17;
当n2﹣1=35时,n2+1=37.
故答案为17;37.
【点睛】本题考查了勾股数的定义.掌握勾股数的定义是解答本题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
(2023·湖北·统考中考真题)
1.如图,在中,,点在边上,且平分的周长,则的长是( )
A. B. C. D.
(2023·四川泸州·统考中考真题)
2.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数,,的计算公式:,,,其中,,是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )
A.3,4,5 B.5,12,13 C.6,8,10 D.7,24,25
(2022·广西桂林·统考中考真题)
3.如图,在ABC中,∠B=22.5°,∠C=45°,若AC=2,则ABC的面积是( )
A. B.1+ C.2 D.2+
(2021·山东滨州·统考中考真题)
4.在中,若,,,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
(2021·四川凉山·统考中考真题)
5.如图,中,,将沿DE翻折,使点A与点B重合,则CE的长为( )
A. B.2 C. D.
(2021·内蒙古鄂尔多斯·统考中考真题)
6.如图,在中,,将边沿折叠,使点B落在上的点处,再将边沿折叠,使点A落在的延长线上的点处,两条折痕与斜边分别交于点N、M,则线段的长为( )
A. B. C. D.
(2022·贵州贵阳·统考中考真题)
7.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
(2021·山东枣庄·统考中考真题)
8.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=,则BC的长是( )
A. B.3 C.3 D.3
二、填空题
(2023·湖北随州·统考中考真题)
9.如图,在中,,D为AC上一点,若是的角平分线,则 .
(2023·山东东营·统考中考真题)
10.一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km至C港,则A,C两港之间的距离为 km.
(2022·内蒙古鄂尔多斯·统考中考真题)
11.如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE=,则AB的长是 .
(2023·四川广安·统考中考真题)
12.如图,圆柱形玻璃杯的杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为 .(杯壁厚度不计)
(2022·黑龙江牡丹江·统考中考真题)
13.在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD= .
(2022·辽宁朝阳·统考中考真题)
14.如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是 .
(2022·湖北黄冈·统考中考真题)
15.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
(2021·江苏宿迁·统考中考真题)
16.《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇生长在它的中央,高出水面部分为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的(示意图如图,则水深为 尺.
(2021·湖南常德·统考中考真题)
17.如图.在中,,平分,于E,若,则的长为 .
(2021·四川内江·统考中考真题)
18.已知,在中,,,,则的面积为 .
三、解答题
(2021·四川攀枝花·统考中考真题)
19.如图是“弦图”的示意图,“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,它标志着中国古代的数学成就.它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,每个直角三角形的两条直角边分别为a、b,斜边为c.请你运用此图形证明勾股定理:a2+b2=c2.
(2022·四川资阳·中考真题)
20.如图,在中,过点C作,在上截取,上截取,连接.
(1)求证:;
(2)若,求的面积.
(2021·湖南长沙·统考中考真题)
21.如图,在中,,垂足为,,延长至,使得,连接.
(1)求证:;
(2)若,,求的周长和面积.
(2020·浙江温州·统考中考真题)
22.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
(2018·甘肃天水·中考真题)
23.如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=,BE=.求CD的长和四边形ABCD的面积.
(2013·吉林·中考真题)
24.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3cm,则BE= cm.
(2019·河北·统考中考真题)
25.已知:整式,整式.
尝试: 化简整式.
发现: ,求整式.
联想:由上可知,,当n>1时为直角三角形的三边长,如图.填写下表中的值:
直角三角形三边
勾股数组Ⅰ / 8
勾股数组Ⅱ /
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】如图所示,过点B作于E,利用勾股定理求出,进而利用等面积法求出,则可求出,再由平分的周长,求出,进而得到,则由勾股定理得.
【详解】解:如图所示,过点B作于E,
∵在中,,
∴,
∵,
∴,
∴,
∵平分的周长,
∴,即,
又∵,
∴,
∴,
∴,
故选C.
【点睛】本题主要考查了勾股定理,正确作出辅助线构造直角三角形是解题的关键.
2.C
【分析】首先证明出,得到a,b是直角三角形的直角边然后由,,是互质的奇数逐项求解即可.
【详解】∵,
∴.
∵,
∴.
∴a,b是直角三角形的直角边,
∵,是互质的奇数,
∴A.,
∴当,时,,,,
∴3,4,5能由该勾股数计算公式直接得出;
B.,
∴当,时,,,,
∴5,12,13能由该勾股数计算公式直接得出;
C.,,
∵,是互质的奇数,
∴6,8,10不能由该勾股数计算公式直接得出;
D.,
∴当,时,,,,
∴7,24,25能由该勾股数计算公式直接得出.
故选:C.
【点睛】本题考查了勾股数的应用,通过,,是互质的奇数这两个条件去求得符合题意的t的值是解决本题的关键.
3.D
【分析】如图,过点A作AD⊥AC于A,交BC于D,过点A作AE⊥BC于E,先证明△ADC是等腰直角三角形,得AD=AC=2,∠ADC=45°,CD=AC=2,再证明AD=BD,计算AE和BC的长,根据三角形的面积公式可解答.
【详解】解:如图,过点A作AD⊥AC于A,交BC于D,过点A作AE⊥BC于E,
∵∠C=45°,
∴△ADC是等腰直角三角形,
∴AD=AC=2,∠ADC=45°,CD=AC=2,
∵∠ADC=∠B+∠BAD,∠B=22.5°,
∴∠DAB=22.5°,
∴∠B=∠DAB,
∴AD=BD=2,
∵AD=AC,AE⊥CD,
∴DE=CE,
∴
∴△ABC的面积.
故选:D.
【点睛】本题考查的是勾股定理,等腰直角三角形的性质,三角形的面积,熟知掌握等腰三角形的性质是解本题的关键.
4.D
【分析】根据题意画出图形,然后作CD⊥AB于点D,根据勾股定理可以求得AB的长,然后根据面积法,可以求得CD的长.
【详解】解:作CD⊥AB于点D,如右图所示,
∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵,
∴,
解得CD=2.4,
故选:D.
【点睛】本题考查勾股定理、三角形的面积,解答本题的关键是明确题意,画出相应的图形,利用勾股定理和面积法解答.
5.D
【分析】先在RtABC中利用勾股定理计算出AB=10,再利用折叠的性质得到AE=BE,AD=BD=5,设AE=x,则CE=AC-AE=8-x,BE=x,在Rt△BCE中根据勾股定理可得到x2=62+(8-x)2,解得x,可得CE.
【详解】解:∵∠ACB=90°,AC=8,BC=6,
∴AB==10,
∵△ADE沿DE翻折,使点A与点B重合,
∴AE=BE,AD=BD=AB=5,
设AE=x,则CE=AC-AE=8-x,BE=x,
在Rt△BCE中
∵BE2=BC2+CE2,
∴x2=62+(8-x)2,解得x=,
∴CE==,
故选:D.
【点睛】本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理.
6.B
【分析】利用勾股定理求出AB=10,利用等积法求出CN=,从而得AN=,再证明∠NMC=∠NCM=45°,进而即可得到答案.
【详解】解:∵
∴AB=,
∵S△ABC=×AB×CN=×AC×BC
∴CN=,
∵AN=,
∵折叠
∴AM=A'M,∠BCN=∠B'CN,∠ACM=∠A'CM,
∵∠BCN+∠B'CN+∠ACM+∠A'CM=90°,
∴∠B'CN +∠A'CM=45°,
∴∠MCN=45°,且CN⊥AB,
∴∠NMC=∠NCM=45°,
∴MN=CN=,
∴A'M=AM=AN MN=-=.
故选B.
【点睛】本题考查了翻折变换,勾股定理,等腰直角三角形的性质,熟练运用折叠的性质是本题的关键.
7.B
【分析】根据图形分析可得小正方形的边长为两条直角边长的差,据此即可求解.
【详解】图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是.
故选B.
【点睛】本题考查了以弦图为背景的计算题,理解题意是解题的关键.
8.B
【分析】折叠的性质主要有:1.重叠部分全等;2.折痕是对称轴,对称点的连线被对称轴垂直平分. 由折叠的性质可知,所以可求出∠AFB=90°,再直角三角形的性质可知,所以,的长可求,再利用勾股定理即可求出BC的长.
【详解】解:
AB=AC,
,
故选B.
【点睛】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用,求出∠AFB=90°是解题的关键.
9.5
【分析】首先证明,,设,在中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
故答案为:5.
【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
10.50
【分析】根据题意画出图形,易证是直角三角形,利用勾股定理即可求解.
【详解】如图,根据题意,得,,,,
∵
∴
∴
∴在中,
即A,C两港之间的距离为50 km.
故答案为:50
【点睛】本题考查方位角,勾股定理,根据题意画出图形,证明是直角三角形是解题的关键.
11.12
【分析】延长BE交AD于点F,由“ASA”可证△BCE≌△FDE,可得DF=BC=5,BE=EF,由勾股定理可求AB的长.
【详解】如图,延长BE交AD于点F,
∵点E是DC的中点,
∴DE=CE,
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠ D=∠BCE,∠FED=∠BEC,
∴ △BCE≌△FDE(ASA),
∴DF=BC=5,BE=EF,
∴BF=2BE=13,AF=5,
在Rt△ABF中,由勾股定理可得AB=12.
故答案为:12.
【点睛】本题考查了全等三角形的判定和性质,勾股定理,添加恰当辅助线构造全等三角形是本题的关键.
12.10
【分析】如图(见解析),将玻璃杯侧面展开,作关于的对称点,根据两点之间线段最短可知的长度即为所求,利用勾股定理求解即可得.
【详解】解:如图,将玻璃杯侧面展开,作关于的对称点,作,交延长线于点,连接,
由题意得:,
,
∵底面周长为,
,
,
由两点之间线段最短可知,蚂蚁从外壁处到内壁处所走的最短路程为,
故答案为:10.
【点睛】本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
13.3.
【详解】试题分析:如图,过点D作DE⊥AB于E,
∵∠C=90°,AC=6,BC=8,
∴AB=,
∵AD平分∠CAB,
∴CD=DE,
∴S△ABC=AC CD+AB DE=AC BC,
即×6 CD+×10 CD=×6×8,
解得CD=3.
考点:1.角平分线的性质,2.勾股定理
14.18
【分析】由题可知,EF为线段BC的垂直平分线,则CD=BD,由勾股定理可得AC5,则△ACD的周长为AC+AD+CD=AC+AD+BD=AC+AB,即可得出答案.
【详解】解:由题可知,EF为线段BC的垂直平分线,
∴CD=BD,
∵∠ACB=90°,AB=13,BC=12,
∴AC5,
∴△ACD的周长为AC+AD+CD=AC+AD+BD=AC+AB=5+13=18.
故答案为:18.
【点睛】本题考查尺规作图、线段垂直平分线的性质、勾股定理,熟练掌握线段垂直平分线的性质及勾股定理是详解本题的关键.
15.m2+1
【分析】2m为偶数,设其股是a,则弦为a+2,根据勾股定理列方程即可得到结论.
【详解】∵2m为偶数,
∴设其股是a,则弦为a+2,
根据勾股定理得,(2m)2+a2=(a+2)2,
解得a=m2-1,
∴弦长为m2+1,
故答案为:m2+1.
【点睛】本题考查了勾股数,勾股定理,熟练掌握勾股定理是解题的关键.
16.12
【分析】我们可以将其转化为数学几何图形,如图所示,根据题意,可知的长为10尺,则尺,设出尺,表示出水深,根据勾股定理建立方程,求出的方程的解即可得到芦苇的长和水深.
【详解】解:设芦苇长尺,则水深尺,
因为尺,所以尺,
在中,,
.解得,
即水深12尺,芦苇长13尺.
故答案为:12.
【点睛】此题考查勾股定理的实际应用,正确理解题意,构建直角三角形利用勾股定理解决问题是解题的关键.
17.
【分析】证明三角形全等,再利用勾股定理即可求出.
【详解】解:由题意:平分,于,
,,
又为公共边,
,
,
在中,,由勾股定理得:
,
故答案是:.
【点睛】本题考查了三角形全等及勾股定理,解题的关键是:通过全等找到边之间的关系,再利用勾股定理进行计算可得.
18.2或14#14或2
【分析】过点B作AC边的高BD,Rt△ABD中,∠A=45°,AB=4,得BD=AD=4,在Rt△BDC中,BC=4,得CD==5,①△ABC是钝角三角形时,②△ABC是锐角三角形时,分别求出AC的长,即可求解.
【详解】解:过点作边的高,
中,,,
,
在中,,
,
①是钝角三角形时,
,
;
②是锐角三角形时,
,
,
故答案为:2或14.
【点睛】本题考查了勾股定理,三角形面积求法,解题关键是分类讨论思想.
19.见解析
【分析】根据大正方形的面积=小正方形的面积+4个直角三角形的面积证明即可
【详解】解:由题意得大正方形面积,小正方形面积,
4个小直角三角形的面积,
∵大正方形的面积=小正方形的面积+4个直角三角形的面积,
∴.
【点睛】本题主要考查了勾股定理的证明,解题的关键在于能够根据题意知晓大正方形的面积=小正方形的面积+4个直角三角形的面积.
20.(1)证明见解析
(2)
【分析】(1)根据,可以得到,即可用SAS证明得出结论;
(2)根据全等三角形的性质,可以得到,设,则,因为在中,,而在中,,即可列出方程求出三角形的面积.
【详解】(1)证明:∵
∴
又∵
∴;
(2)由(1),
∴,
设,∵,则,
在中,,
在中,,
∴,
即,整理得:,
解得:(舍去),
∴,
∴,,
∴.
【点睛】本题考查了全等三角形的判定和性质,勾股定理的应用,解一元二次方程,用方程思想解决几何问题是本题的关键.
21.(1)证明见解析;(2)周长为,面积为22.
【分析】(1)先根据垂直的定义可得,再根据三角形全等的判定定理与性质即可得证;
(2)先根据全等三角形的性质可得,从而可得,再利用勾股定理可得,从而可得,然后利用勾股定理可得,最后利用三角形的周长公式和面积公式即可得.
【详解】(1)证明:,
,
在和中,,
,
;
(2),,
,
,
,
,
,
,
,
,
,
则的周长为,
的面积为.
【点睛】本题考查了三角形全等的判定定理与性质、勾股定理等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.
22.(1)见解析;(2)13
【分析】根据题意可知,本题考查平行的性质,全等三角形的判定和勾股定理,根据判定定理,运用两直线平行内错角相等再通过AAS以及勾股定理进行求解.
【详解】解:(1)∵
∴
在△ABC和△DCE中
∴△ABC≌△DCE
(2)由(1)可得BC=CE=5
在直角三角形ACE中
【点睛】本题考查平行的性质,全等三角形的判定和勾股定理,熟练掌握判定定理运用以及平行的性质是解决此类问题的关键.
23.CD=2;四边形ABCD的面积是
【分析】利用等腰直角三角形的性质得出EH=DH=1,进而得出再利用直角三角形中30°所对边等于斜边的一半得出CD的长,求出AC,AB的长即可得出四边形ABCD的面积.
【详解】解:如图,过点D作DH⊥AC,
∵∠CED=45°,DH⊥EC,DE=,∴EH=DH.
∵EH2+DH2=ED2,∴EH2=1.∴EH=DH=1.
又∵∠DCE=30°,∴CD=2,HC=.
∵∠AEB=45°,∠BAC=90°,BE=.∴AB=AE=2.
∴AC=2+1+=3+.
∴S四边形ABCD=×2×(3+)+×1×(3+)=.
24.(1)见解析(2)6
【详解】(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE.
∵∠ACB=90°,
∴∠ACB=∠DCE.
∴∠ACB+∠BCD=∠DCE+∠BCD.
∴∠ACD=∠BCE.
∵在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS).
(2)∵AC=BC=3,∠ACB=90°,
∴由勾股定理得:AB=3.
又∵DB=AB,
∴AD=2AB=6.
∵△ACD≌△BCE,
∴BE=AD=6,
故答案为:
25.尝试:;发现:;联想:17,37.
【分析】先根据完全平方公式和整式的混合运算法则求出A,进而求出B,再把n的值代入即可解答.
【详解】A=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2.
∵A=B2,B>0,∴B=n2+1,当2n=8时,n=4,∴n2+1=42+1=17;
当n2﹣1=35时,n2+1=37.
故答案为17;37.
【点睛】本题考查了勾股数的定义.掌握勾股数的定义是解答本题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
