专题1.30勾股定理常考考点分类专题 分层练习提升练习(含解析)2023-2024学年八年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.30勾股定理常考考点分类专题 分层练习提升练习(含解析)2023-2024学年八年级数学上册北师大版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 22:17:23 | ||
图片预览


文档简介
专题1.30 勾股定理常考考点分类专题(分层练习)(提升练习)
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习.
一、单选题
【考点1】勾股定理 勾股数
1.下面各组数中,是勾股数的是( )
A.1,, B.32,42,52 C.1,3,2 D.5,12,13
2.在学习“勾股数”的知识时,爱动脑的小小同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.据此规律,当时,的值是( )
…
…
…
A. B. C. D.
【考点2】勾股定理 勾股树
3.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别为4,6,3,4,则最大正方形E的面积是( )
A.17 B.34 C.77 D.86
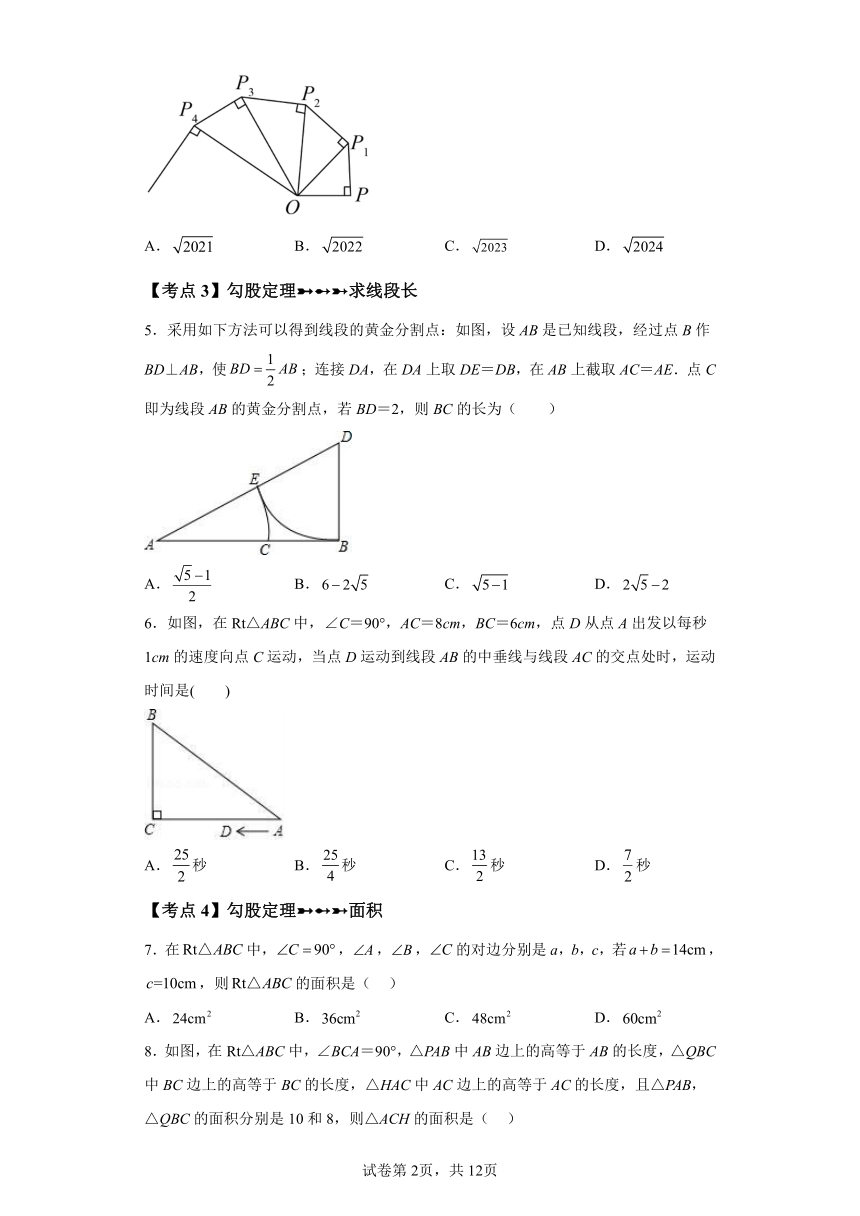
4.如图,,过点P作,且,得;再过点作且,得;又过点作且,得…,依此法继续作下去,得的值为( )
A. B. C. D.
【考点3】勾股定理 求线段长
5.采用如下方法可以得到线段的黄金分割点:如图,设AB是已知线段,经过点B作BD⊥AB,使;连接DA,在DA上取DE=DB,在AB上截取AC=AE.点C即为线段AB的黄金分割点,若BD=2,则BC的长为( )
A. B. C. D.
6.如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D从点A出发以每秒1cm的速度向点C运动,当点D运动到线段AB的中垂线与线段AC的交点处时,运动时间是( )
A.秒 B.秒 C.秒 D.秒
【考点4】勾股定理 面积
7.在中,,,,的对边分别是a,b,c,若,,则的面积是( )
A. B. C. D.
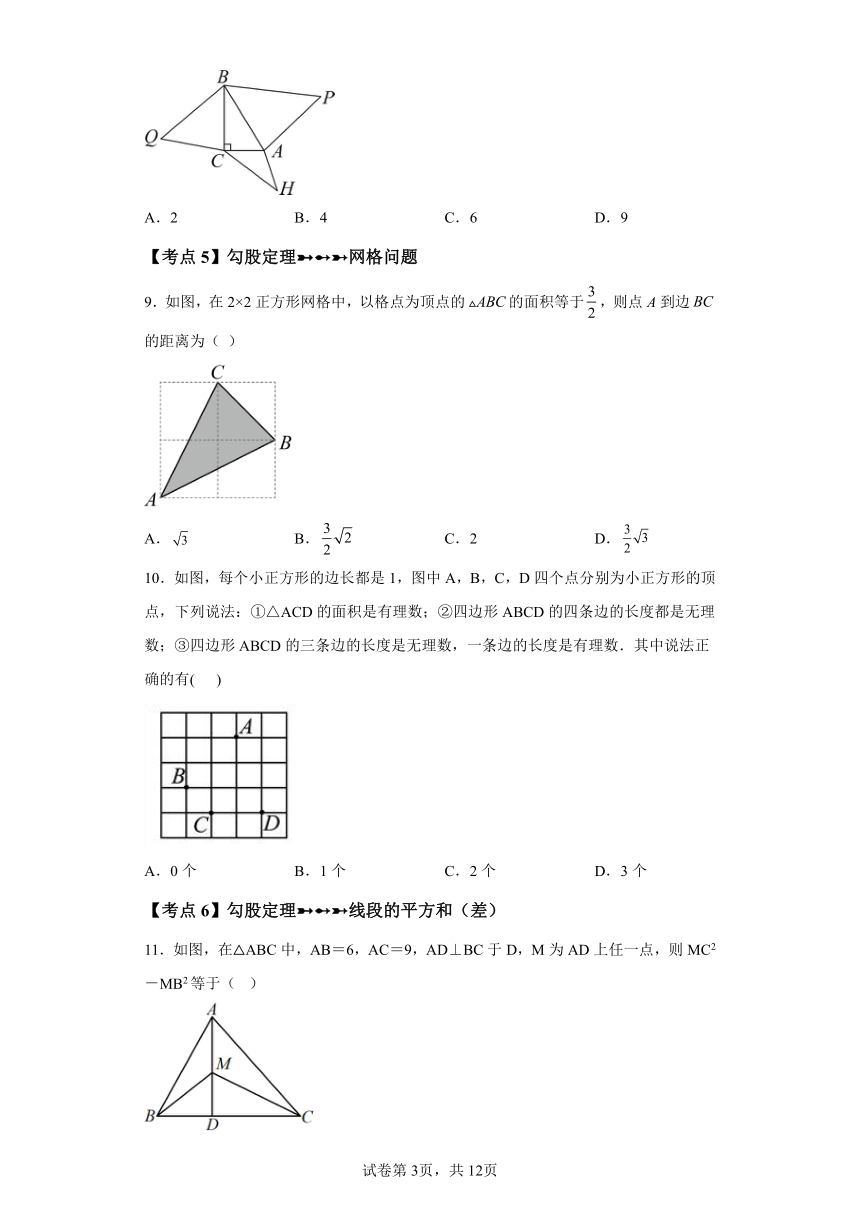
8.如图,在Rt△ABC中,∠BCA=90°,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )
A.2 B.4 C.6 D.9
【考点5】勾股定理 网格问题
9.如图,在2×2正方形网格中,以格点为顶点的的面积等于,则点A到边的距离为( )
A. B. C.2 D.
10.如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:①△ACD的面积是有理数;②四边形ABCD的四条边的长度都是无理数;③四边形ABCD的三条边的长度是无理数,一条边的长度是有理数.其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
【考点6】勾股定理 线段的平方和(差)
11.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
12.若直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,则有( )
A. B.+= C.+= D.
【考点7】勾股定理的逆定理 判定三角形的形状
13.学校的书香苑呈三角形形状,三边分别是9,12,15,那么书香苑的面积是( )
A.135 B.180 C.108 D.54
14.已知a、b、c是三角形的三边长,若满足,则这个三角形的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.直角三角形
【考点8】勾股定理的逆定理 弦图问题
15.我国清代数学家李锐借助三个正方形用出入相补的方法证明了勾股定理.如图,设直角三角形两直角边的长分别为a、b(),斜边的长为c.作三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使E、F、G三点在一条直线上,若,四边形与面积之和为13.5,则正方形的面积为( )
A.32 B.36 C.46 D.49
16.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,若,大正方形面积为15,则小正方形面积为( )
A.3 B.4 C.6 D.12
【考点9】勾股定理的逆定理 勾股定理与无理数
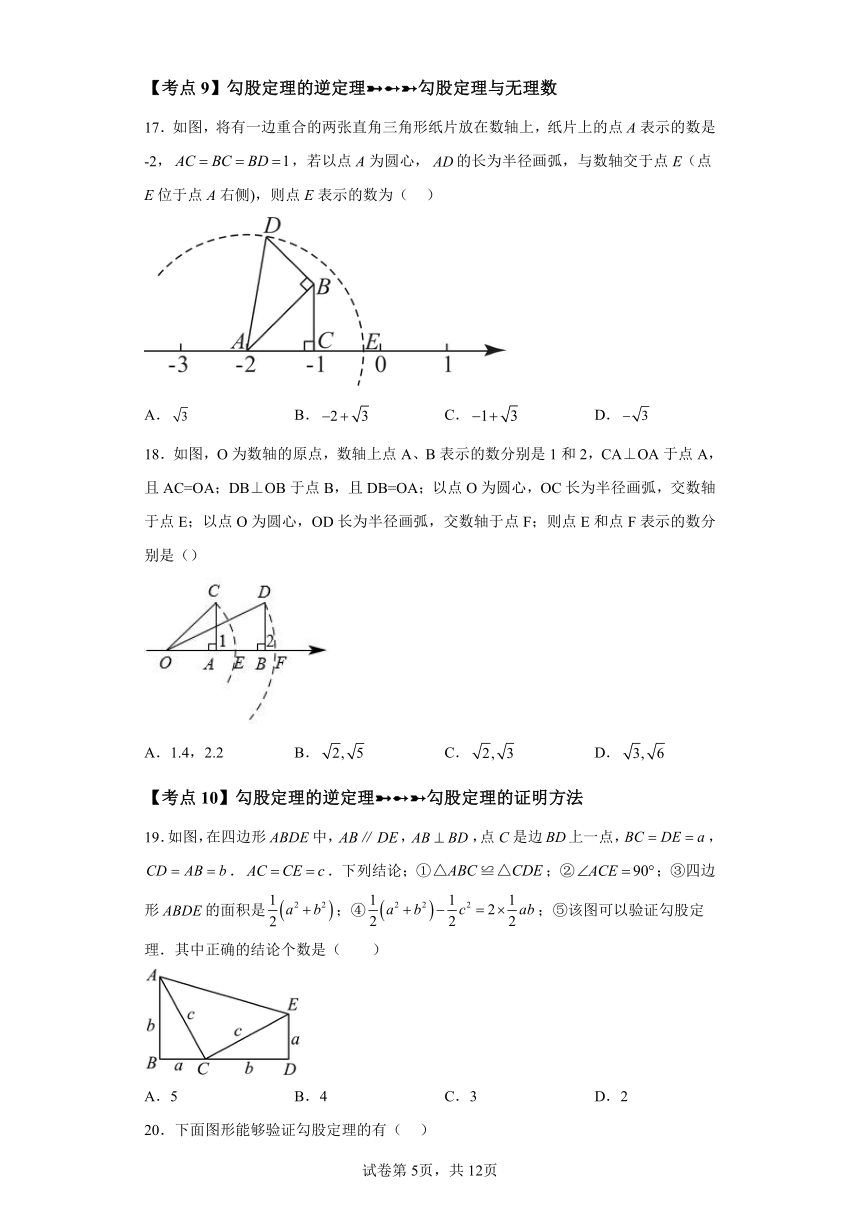
17.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,,若以点A为圆心,的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为( )
A. B. C. D.
18.如图,O为数轴的原点,数轴上点A、B表示的数分别是1和2,CA⊥OA于点A,且AC=OA;DB⊥OB于点B,且DB=OA;以点O为圆心,OC长为半径画弧,交数轴于点E;以点O为圆心,OD长为半径画弧,交数轴于点F;则点E和点F表示的数分别是()
A.1.4,2.2 B. C. D.
【考点10】勾股定理的逆定理 勾股定理的证明方法
19.如图,在四边形中,,,点C是边上一点,,..下列结论;①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.5 B.4 C.3 D.2
20.下面图形能够验证勾股定理的有( )
A.4个 B.3个 C.2个 D.1个
【考点11】勾股定理的逆定理 用勾股定理构造图形解决问题
21.平面内,将长分别为2,4,3的三根木棒按如图方式连接成折线,其中可以绕点任意旋转,保持,将,两点用绷直的皮筋连接,设皮筋长度为,则不可能是( )
A.3 B.5 C.7 D.8
22.《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绸索,绳索从木柱上端顺木桂下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部9尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为( )
A. B.
C. D.
【考点12】勾股定理的逆定理 用勾股定理与折叠问题
23.如图,在,,,沿过点A的直线折叠,使点B落在边上的点D处,再次折叠,使点C与点D重合,折痕交于点E,则的长度为( )
A. B. C. D.
24.如图,将一张正方形纸片对折,使与重合,得到折痕后展开,E为上一点,将沿所在的直线折叠,使得点C落在折痕上的点F处,连接.若,则的长度为( )
A. B. C. D.
二、填空题
【考点1】勾股定理 勾股数
25.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑥组勾股数为 .
26.勾股定理本身就是一个关于,,的方程,满足这个方程的正整数解常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:,,,…,分析上面勾股数组可以发现,,,,…分析上面规律,第6个勾股数组为 .
【考点2】勾股定理 勾股树
27.如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13,则图中所有的正方形的面积之和为 .
28.如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的面积为40,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x+y= .
【考点3】勾股定理 求线段长
29.定义:如图,点P、Q把线段AB分割成线段AP、PQ和BQ,若以AP、PQ、BQ为边的三角形是一个直角三角形,则称点P、Q是线段AB的勾股分割点.已知点P、Q是线段AB的勾股分割点,如果AP=8,PQ=12(PQ>BQ),那么BQ= .
30.如图1,点,为边长为8cm的正方形边,上的动点,连接,点为边的中点.将正方形沿线段折叠,使点的对应点落在线段上,点的对应点为,如图2所示.则线段的取值范围是 .
【考点4】勾股定理 面积
31.如图所示,四边形ADEF为正方形,ABC为等腰直角三角形,D在BC边上,△ABC的面积等于98,BD:DC=2:5,则正方形ADEF的面积等于 .
32.在中,,边上的高为15,则的面积是 .
【考点5】勾股定理 网格问题
33.如图,将放在每个小正方形的边长为1的网格中,点均落在格点上.
(1)的面积等于________.
(2)请在如图所示的网格中,用无刻度的直尺,过点画一条直线,交于点,使的面积等于面积的3倍,并简要说明画图的方法__________.(不要求证明)
34.如图,在每个小正方形的边长为1的网格中,A,B为格点在如图所示的网格中求作一点C,使得且的面积等于,则此时的长为 .
【考点6】勾股定理 线段的平方和(差)
35.如图,已知,直角中,,从直角三角形两个锐角顶点所引的中线的长,,则斜边AB之长为 .
36.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形,对角线交于点,若,则 .
【考点7】勾股定理的逆定理 判定三角形的形状
37.有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为 .
38.已知三角形的三边长之比为,则此三角形的形状是 .
【考点8】勾股定理的逆定理 弦图问题
39.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若,大正方形的面积为,则的长为 .
40.如图1,将长为,宽为的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到两个正方形.
(1)图2中小正方形的边长为___________(用含的代数式表示):
(2)当时,该大正方形的面积是___________.
【考点9】勾股定理的逆定理 勾股定理与无理数
41.如图,矩形的边在数轴上,其中点A,B分别表示数,2,,以点B为圆心,长为半径作弧交数轴于点P,则点P表示的数为 .
42.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2022个等腰直角三角形的斜边长是 .
【考点10】勾股定理的逆定理 勾股定理的证明方法
43.如图所示的正方形图案是用4个全等的直角三角形拼成的.已知正方形的面积为25,正方形的面积为1,若用、分别表示直角三角形的两直角边,下列三个结论:①;②;③;④.其中正确的是 (填序号).
44.如图,两个边长分别为a,b,c的直角三角形和一个两条直角边长都是的直角三角形拼成如图形状用不同的方法计算这个图形的面积,可得关于a,b,c的一个等式是 .
【考点11】勾股定理的逆定理 用勾股定理构造图形解决问题
45.如图, 是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为,面积是25的正方形的四个顶点分别在这四条直线上,那么的值是 .
46.已知,在中,,高,则边长为 .
【考点12】勾股定理的逆定理 用勾股定理与折叠问题
47.已知中,,,,将它的一条直角边沿一锐角角平分线所在直线翻折,使直角顶点落在斜边上,则折叠后不重合部分三角形的面积为 .
48.如图,三角形纸片,点是边上一点,连接,把沿着翻折,得到,与交于点,连接交于点若,,,的面积为,则点到的距离为 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据勾股定理即可解答.
【详解】A、,则不构成勾股数,故本选项不符合题意.
B、,则不构成勾股数,故本选项不符合题意.
C、,则不构成勾股数,故本选项不符合题意.
D、,构成勾股数,故本选项符合题意.
故选:D.
【点睛】本题考查了勾股数,熟练掌握勾股定理是解题的关键.
2.B
【分析】由表格中的数据得:,,即可求出的值.
【详解】解:由表格中的数据得:,,
,
当时,,
.
故选:.
【点睛】本题考查了勾股数,掌握表中数据的变化规律,找到数据的关系是解答本题的关键.
3.C
【分析】根据正方形的面积公式,结合勾股定理,能够导出正方形A,B,C,D的面积和即为最大正方形的面积.
【详解】解:如下图:
根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,
S1=42+62,S2=32+42,
于是S3=S1+S2,
即可得S3=16+36+9+16=77.
故选:C.
【点睛】本题考查了勾股定理的知识,根据勾股定理的几何意义表示出S3是解答本题的关键.
4.C
【分析】根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
【详解】解:∵OP=1,,,
同理:,
∴,
故选:C .
【点睛】本题考查了勾股定理的应用,解此题的关键是能根据求出的结果得出规律.
5.B
【分析】由勾股定理求出AD=2,则AC=AE=AD﹣DE=2﹣2,得BC=AB﹣AC=6﹣2即可.
【详解】解:∵BD⊥AB,,BD=2,
∴AB=4,
∴AD===2,
∵DE=BD=2,
∴AC=AE=AD﹣DE=2﹣2,
∴BC=AB﹣AC=4﹣(2﹣2)=6﹣2;
故选:B.
【点睛】本题考查勾股定理,掌握勾股定理是解题的关键.
6.B
【分析】画出图形,根据勾股定理解答即可.
【详解】如图所示:
中,,,,
,
是的中垂线,
,
连接,
,
在中,,
即,
解得:,
当点运动到的中垂线与线段AC的交点时,运动时间为秒.
故选.
【点睛】此题考查勾股定理的应用,线段垂直平分线的性质,关键是根据勾股定理构建直角三角形进行解答.
7.A
【分析】根据题意可知,的面积为,结合已知条件,根据完全平方公式变形求值即可.
【详解】解:中,,,,所对的边分别为a,b,c,
,
∵,,
∴,
,故A正确.
故选:A.
【点睛】本题主要考查了勾股定理,完全平方公式变形求值,解题的关键是将完全平方公式变形求出ab的值.
8.A
【分析】根据勾股定理可求AC2+BC2=AB2,再根据三角形的面积公式即可求解.
【详解】解:在Rt△ABC中,∠BCA=90°,
∴AC2+BC2=AB2,
∴AC2+BC2=AB2,
∵△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,
∴△ACH的面积是10﹣8=2.
故选:A.
【点睛】本题考查勾股定理,熟知勾股定理是解题的关键.
9.B
【分析】根据勾股定理计算出的长,再根据三角形的面积,即可求出点A到边的距离.
【详解】解:设点A到边的距离为h,
∵,,
∴,
∴点A到边的距离为,
故选B.
【点睛】本题主要考查了勾股定理的应用,掌握面积法是关键.
10.C
【详解】①∵△ACD的面积=×2×3=3,
∴①说法正确;
②∵CD=2,
∴说法②错误;
③由勾股定理得:AB=,
∴说法③正确;
正确的说法有2个.
故选C.
11.D
【分析】在Rt△ABD及Rt△ADC中可分别表示出BD2及CD2,在Rt△BDM及Rt△CDM中分别将BD2及CD2的表示形式代入表示出BM2和MC2,然后作差即可得出结果.
【详解】解:在Rt△ABD和Rt△ADC中,
BD2=AB2 AD2,CD2=AC2 AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2 AD2+MD2,MC2=CD2+MD2=AC2 AD2+MD2,
∴MC2 MB2=(AC2 AD2+MD2) (AB2 AD2+MD2)
=AC2 AB2
=45.
故选:D.
【点睛】本题考查了勾股定理的知识,题目有一定的技巧性,比较新颖,解答本题需要认真观察,分别两次运用勾股定理求出MC2和MB2是本题的难点,重点还是在于勾股定理的熟练掌握.
12.C
【分析】根据三角形的面积求法,可将斜边的高h用两直角边表示出来.
【详解】∵直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,
∵ab=ch,
∴h=,
∴,
∴+===.
故选C.
【点睛】本题主要考查勾股定理以及三角形的面积公式,根据勾股定理结合三角形的面积公式,进行适当的变形,是解题的关键.
13.D
【详解】试题解析:∵在△ABC中,三条边的长度分别为9、12、15,92+122=152,
∴△ABC是直角三角形,
∴书香苑的面积是.
故选D.
14.D
【分析】首先根据绝对值,平方数与算术平方根的非负性,求出a,b,c的值,在根据勾股定理的逆定理判断其形状是直角三角形.
【详解】∵(a-6)2≥0,≥0,|c-10|≥0,
∴a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴这个三角形是直角三角形.
故选D.
【点睛】本题主要考查了非负数的性质与勾股定理的逆定理,此类题目在考试中经常出现,是考试的重点.
15.B
【分析】证明≌,得到,再证明≌,从而推出,化简得到,再根据,得到,结合两式可得,从而计算结果.
【详解】解:在与中,
,
∴≌(HL),
∴,
∴,
又∵,
∴,
∴,
在与中,
,
∴≌(ASA),
∴
,
∴,
即,
化简得:①,
又∵,
∴,
∴②,
,得:,
∴.
故选B.
【点睛】本题考查了勾股定理,全等三角形的判定和性质,解题的关键是证明三角形全等,根据图形面积得到相应等式,从而进行计算.
16.A
【分析】观察图形可知,小正方形的面积=大正方形的面积减去4个直角三角形的面积,利用已知,大正方形的面积为15,可以得出4个直角三角形的面积,进而求出答案.
【详解】解:∵,
∴,
∵直角三角形的较长直角边长为a,较短直角边长为b,
∴大正方形的边长为.
∵大正方形的面积为15,
∴,
∴
∴,
∴小正方形的面积为.
故选:A.
【点睛】此题考查了完全平方公式,以及勾股定理的应用,熟练应用勾股定理是解题关键.
17.B
【详解】根据勾股定理得:,,
∴,
∴,
∴点表示的数为.
故答案为:B.
【点睛】此题主要考查了勾股定理,以及数轴与实数,解题时求数轴上两点间的距离应让较大的数减去较小的数即可,本题的关键是求出AE的长.
18.B
【解析】根据勾股定理及数轴性质解答 .
【详解】解:由题意可得:
,
,
∴点E和点F表示的数分别是,
故选B.
【点睛】本题考查勾股定理及数轴的综合应用,熟练掌握勾股定理的应用及用数轴表示数的方法是解题关键.
19.C
【分析】证明,由全等三角形的性质可得出,.再由图形的面积可得出①②⑤正确.
【详解】解:,,
,
.
在和中,
,
,
,.
,
.
,
,
故①②正确;
,,
四边形的面积是;
故③错误;
梯形的面积直角三角形的面积两个直角三角形的面积,
,
,,
故④错误,故⑤正确
故①②⑤共3个正确,③④错误.
故选:C.
【点睛】本题考查了全等三角形的判定及性质的运用,勾股定理的证明,垂直的判定及性质的运用,解答时证明三角形全等是关键.
20.A
【分析】分别计算图形的面积进行证明即可.
【详解】解:第一个图:由,可得,故该项的图形能够验证勾股定理;
第二个图:由,可得,故该项的图形能够验证勾股定理;
第三个图:由,可得,故该项的图形能够验证勾股定理;
第四个图:由,可得,故该项的图形能够验证勾股定理;
故选:A.
【点睛】此题考查了图形与勾股定理的推导,熟记勾股定理的计算公式及各种图形面积的计算方法是解题的关键.
21.D
【分析】连接,根据勾股定理可得的长,在分两种情况讨论即可;
【详解】连接,则.
如图1,当点在线段上时,;
如图2,当点在的延长线上时,,
∴的取值范围为,
故选:D.
【点睛】本题主要考查了勾股定理的应用、三角形的三边关系,解题的关键是构造直角三角形,利用勾股定理求出.
22.C
【分析】设绳索长为x尺,根据勾股定理列出方程解答即可.
【详解】解:设绳索长为x尺,可列方程为,
故选:C.
【点睛】本题考查了由实际问题抽象出方程,勾股定理的应用,找准等量关系,正确列出方程是解题的关键.
23.B
【分析】根据题意可得,,,,可得,继而设,则,根据勾股定理即可求解.
【详解】解:∵沿过点A的直线将纸片折叠,使点B落在边上的点D处,
∴,,
∵折叠纸片,使点C与点D重合,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得,
即,
故选:B
【点睛】本题考查了折叠的性质,勾股定理,掌握折叠的性质以及勾股定理是解题的关键.
24.A
【分析】由正方形可得,再由折叠可得,,,,利用勾股定理可求的长,进而得到,在中,利用勾股定理构造方程,即可求得的长.
【详解】解:∵四边形是正方形
∴
由折叠可得,,,
故选:A.
【点睛】本题只要考查折叠问题中勾股定理的运用,在这类问题中利用勾股定理构造方程是常用的方法.
25.16,63,65
【分析】据前面的几组数可以得到每组勾股数与各组的序号之间的关系,如果是第n组数,则这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1.根据这个规律即可解答.
【详解】解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1,
故可得第⑥组勾股数是16,63,65.
故答案为选:16,63,65.
【点睛】本题考查了勾股数,此题属规律性题目,解答此题的关键是根据所给的勾股数找出规律,按照此规律即可解答.
26.13,84,85
【分析】由勾股数组:(3,4,5),(5,12,13),(7,24,25)…中,4=1×(3+1),12=2×(5+1),24=3×(7+1),…可得第6组勾股数中间的数为6×(13+1)=84,进而得出(13,84,85).
【详解】解:∵第1组:3=2×1+1,4=1×(3+1),5=4+1;
第2组:5=2×2+1,12=2×(5+1),13=12+1;
第3组:7=2×3+1,24=3×(7+1),25=24+1;
∴第n组:2n+1,n(2n+1+1),n(2n+1+1)+1,
∴第6组:2×6+1=13,6×(13+1)=84,84+1=5.
故答案为:13,84,85.
【点睛】本题考查的是勾股数的规律探究,能够根据题意找到每组勾股数之间的关系是解决本题的关键.
27.507
【分析】根据勾股定理有S正方形2+S正方形3=S正方形1,S正方形C+S正方形D=S正方形3,S正方形A+S正方形B=S正方形2,等量代换即可求所有正方形的面积之和.
【详解】解:如图所示,
根据勾股定理可知,
S正方形2+S正方形3=S正方形1,
S正方形C+S正方形D=S正方形3,
S正方形A+S正方形B=S正方形2,
∴S正方形C+S正方形D+S正方形A+S正方形B
=S正方形2+S正方形3
=S正方形1,
则S正方形1+正方形2+S正方形3+S正方形C+S正方形D+S正方形A+S正方形B
=3S正方形1
=3×132
=3×169
=507.
故答案为507
【点睛】本题考查了勾股定理.有一定难度,注意掌握直角三角形中,两直角边的平方和等于斜边的平方.
28.22
【分析】如图,先表示出正方形B的面积,继而观察图形得出正方形A、B的面积差,列式整理即可求得答案.
【详解】如图,由图可看出,正方形B的面积等于10+x,
正方形A与正方形B的面积的差等于8+y,
又正方形A的面积为40,
所以8+y=40-(10+x),
所以x+y=22,
故答案为22.
【点睛】此题结合正方形的面积公式以及勾股定理发现各正方形的面积之间的关系,正确把握和灵活运用相关知识是解题的关键.
29.4
【分析】由题干中勾股分割点的定义可得:AP2+BQ2=PQ2,据此即可解答.
【详解】解:由题意可得,AP2+BQ2=PQ2,即82+BQ2=122,解得BQ=4,
故答案为4.
【点睛】本题考查了勾股定理的运用,理解题意并确定三条线段谁是直角边、谁是斜边是解题关键.
30.
【分析】当点P 与点B 重合时,CN 取得最小值0;当点P 与点E 重合时,CN 取得最大值,根据正方形边长为8,点为边的中点,设CN=x,则,CE=4,根据,利用勾股定理即可得出CN的长,取两种情况的中间值即可得到线段的取值范围.
【详解】当点P 与点B 重合时,CN 取得最小值0;
当点P 与点E 重合时,CN 取得最大值
如图,
正方形边长为8,点为边的中点
设CN=x,则,CE=4
在中,
即
解得
此时,
所以,线段的取值范围是.
故答案为:.
【点睛】本题考查了折叠问题,涉及正方形的性质、勾股定理的应用,熟练掌握知识点是解题的关键.
31.116
【分析】过点A作,交BC于点H,根据等腰直角三角形的性质可得:,利用三角形面积公式可得:,然后根据勾股定理得出:,根据题意BD:DC=2:5,结合,可得,,在中,利用勾股定理可得正方形的边长,根据正方形面积公式即可求出面积.
【详解】解:过点A作,交BC于点H,
∴,
∵等腰直角的面积等于98,
∴,
∴,
又∵BD:DC=2:5,
∴,,
在中,
,
∴正方形ABCD的面积:.
故本题答案为:116.
【点睛】题目主要考查等腰直角三角形的性质、线段比及勾股定理,作出辅助线应用勾股定理是解题关键.
32.或
【分析】分是锐角和是钝角两种情况,进行求解即可.
【详解】解:①当点D在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
②当点D不在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
综上:的面积是或.
【点睛】本题考查勾股定理.解题的关键是画出图形,利用分类讨论的思想进行求解.
33.(1)2
(2)见解析
【分析】(1)根据三角形的面积公式,即可求出答案;
(2)根据题意,在上取,即可画出图形.
【详解】(1)解:;
(2)解:如图:找的四等分点,连接为所求.
作法:①取线段,在线段取一点,使,
②过作的平行线,使,交于点,
③作直线.
则直线就是所求作的直线.
【点睛】本题考查了复杂作图,以及三角形的面积,解题的关键是学会利用分割法求三角形面积,巧妙利用格点作四等分点,属于作图中比较难的题目.
34.
【分析】的面积等于,,确定点C所在的位置,即可求解.
【详解】∵,
∴
∵的面积等于,
∴点C所在的位置如图所示,
∴
故答案为:
【点睛】本题考查勾股定理求三角形线段的长,解题的关键是确定点C所在的位置.
35.8
【分析】设BC=x,AC=y,根据勾股定理列方程组,从而可求得斜边的平方,即求得斜边的长.
【详解】设BC=x,AC=y,
∵直角三角形两个锐角顶点所引的中线
∴
在Rt△ADC和Rt△BCE中,由勾股定理得:
∴
∴
∴
故答案为:8
【点睛】注意此题的解题技巧:根据已知条件,在两个直角三角形中运用勾股定理列方程组.求解的时候,注意不必分别求出未知数的值,只需求出两条直角边的平方和,运用勾股定理即可.
36.136
【分析】在Rt△BOC和Rt△AOD中,根据勾股定理得,, 在Rt△AOB和Rt△COD中,根据勾股定理得,,进一步得,最后求得.
【详解】解:,
,
在Rt△BOC和Rt△AOD中,根据勾股定理得,,
在Rt△AOB和Rt△COD中,根据勾股定理得,,
, ,
;
故答案为:.
【点睛】本题考查勾股定理的应用,熟练掌握勾股定理在实际问题中的应用,从题中抽象出勾股定理这一数学模型是解题关键.
37.234m2
【分析】连接AC,则△ABC和△ACD均为直角三角形,根据AB,BC可以求出AC,根据AC,CD可以求出AD,根据直角三角形面积计算可以求出△ABC和△ACD的面积,四边形ABCD的面积为两个直角三角形面积之和.
【详解】连接AC,
在Rt△ABC中,AC为斜边,
则AC===25(m),
在Rt△ACD中,AC为斜边,则AD==═24(m),
四边形ABCD面积S=AB×BC+AD×CD=×20×15+×7×24=234(m2).
故答案为234m2.
【点睛】本题考查了勾股定理在实际生活中的应用以及直角三角形面积计算,本题中正确的运用勾股定理计算AC是解题的关键.
38.等腰直角三角形
【分析】由已知得其有两条边相等,并且符合勾股定理的逆定理,从而可判断三角形的形状.
【详解】解:由题意设三边长分别为:x,x,x
∴三角形一定为直角三角形,并且是等腰三角形.
故答案为等腰直角三角形.
【点睛】本题考查了勾股定理的逆定理,三角形三边关系满足a2+b2=c2,三角形为直角三角形.
39.
【分析】由题意可知:中间小正方形的边长为:,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.
【详解】由题意可知:中间小正方形的边长为:,
∵大正方形的面积为
∴,
又∵,
∴,
∴,即
∴
故答案为.
【点睛】本题考查了勾股定理的证明,熟练掌握该知识点是本题解题的关键.
40.(1)
(2)17
【分析】(1)观察图形,用直角三角形较长的直角边减去较短的直角边即可;
(2)当时,求出大正方形的边长即可求其面积.
【详解】(1)解:∵直角三角形较短的直角边,
较长的直角边,
∴小正方形的边长;
故答案为:;
(2)解:当时,大正方形的边长,
∴大正方形的面积.
故答案为:17
【点睛】本题考查了列代数式,代数式求值,观察图形,用直角三角形较长的直角边减去较短的直角边求出小正方形的边长是解题的关键.
41.##
【分析】根据勾股定理求出,,再利用数轴上两点间距离即可求出点P.
【详解】解:∵,
∴,
∴,
∴点P表示的数为:.
故答案为:.
【点睛】本题考查了实数与数轴的关系,在数轴上表示无理数,其中利用距离求点是解题的关键.
42.21011
【分析】先根据勾股定理计算第1个,第2个,第3个,第4个等腰直角三角形的斜边长,找到规律后即可求出第2022个等腰直角三角形的斜边长.
【详解】根据勾股定理可得
第1个Rt△ABC的斜边AC=;
第2个Rt△ACD的斜边AD=;
第3个Rt△ADE的斜边AE=;
第4个Rt△AEF的斜边AF=;
......
第n个等腰直角三角形的斜边=;
∴第2022个等腰直角三角形的斜边=.
【点睛】本题考查了勾股定理及找规律求等腰直角三角形的斜边长,找到规律是解题的关键.
43.①②③
【分析】用含有的代数式分别表示小正方形及大正方形的边长,然后根据面积关系得出与的关系式,依次判断所给关系式即可.
【详解】解:由题意可得小正方形的边长=1,大正方形的边长=5,
斜边2=大正方形的面积,
故①正确;
∵小正方形的边长为1,
,
故②正确;
∵小正方形的面积+四个直角三角形的面积等于大正方形的面积,
,
,
故③正确;
,
故④不正确.
综上可得①②③正确.
故答案为:①②③.
【点睛】本题考查了勾股定理的证明,完全平方公式的变形应用等知识,根据所给图形,利用面积关系判断与的关系是解答本题的关键.
44.
【分析】用两种方法求图形面积,一是直接利用梯形面积公式来求;一是利用三个三角形面积之和来求.
【详解】根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b) =ab+ab+c2,即(a+b)(a+b) =ab+ab+c2,
整理得:a2+b2=c2.
故答案为:a2+b2=c2.
【点睛】本题考查了勾股定理的证明,整式的混合运算,熟练掌握运算法则是解本题的关键.
45.
【分析】过点作构造全等三角形,利用全等三角形的性质得到关于正方形面积的方程,然后解方程求解即可.
【详解】解:过点作交于点,交于点,
在正方形中,
又
∵正方形的面积为25,
或(舍去)
故答案为:
【点睛】本题主要考查全等三角形及勾股定理和正方形面积的关系,通过辅助线构造全等三角形并利用勾股定理列方程是解决本题的关键.
46.7或5
【分析】根据题意画出符合条件的图形,分别考虑当高AD在内部和外部的情况,再用勾股定理求解.
【详解】
如图:当AD在△ABC内部时,
∵,,
∴,,
∴BC=6+1=7;
如图:当AD在△ABC外部时,
∵,,
∴,,
∴BC=6-1=5;
故答案为:7或5
【点睛】本题主要考查了用勾股定理求三角形的边,熟练地掌握勾股定理的内容,根据题意进行分类讨论是解题的关键.
47.或6
【分析】首先利用勾股定理求出的斜边的长,然后根据题意,分两种情况画出图形,利用折叠的性质和勾股定理求解即可.
【详解】解:在中,,,,
∴,
可分两种情况:
第一种情况:如图1,不重合部分是,
∵直角边沿的平分线所在直线翻折,直角顶点C落在斜边上点D处,
∴,,,
∴,
设,则,
∴,即,
解得,
∴,
∴;
第二种情况:如图2,不重合部分是,
∵直角边沿的平分线所在直线翻折,直角顶点C落在斜边上点D处,
∴,,
∴,
设,则,
∴,即,
解得,
∴,
∴;
综上所述,折叠后不重合部分三角形的面积为或6.
故答案为:或6.
【点睛】本题是几何变换综合题,考查了勾股定理、折叠的性质的知识.根据题意分情况计算是解答本题的关键.
48.
【分析】先求出的面积.根据三角形的面积公式求出,设点到的距离为,根据,求出即可解决问题.
【详解】解:,
,
,
由翻折可知,≌,,
,,
,
,
,
,
设点到的距离为,则有,
,
故答案为:.
【点睛】本题考查翻折变换的性质,三角形的面积,勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数构建方程解决问题.
答案第1页,共2页
答案第1页,共2页
特别说明:本专题涉及到二次根式的运算,建议学习第二章《实数》后讲行练习.
一、单选题
【考点1】勾股定理 勾股数
1.下面各组数中,是勾股数的是( )
A.1,, B.32,42,52 C.1,3,2 D.5,12,13
2.在学习“勾股数”的知识时,爱动脑的小小同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.据此规律,当时,的值是( )
…
…
…
A. B. C. D.
【考点2】勾股定理 勾股树
3.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别为4,6,3,4,则最大正方形E的面积是( )
A.17 B.34 C.77 D.86
4.如图,,过点P作,且,得;再过点作且,得;又过点作且,得…,依此法继续作下去,得的值为( )
A. B. C. D.
【考点3】勾股定理 求线段长
5.采用如下方法可以得到线段的黄金分割点:如图,设AB是已知线段,经过点B作BD⊥AB,使;连接DA,在DA上取DE=DB,在AB上截取AC=AE.点C即为线段AB的黄金分割点,若BD=2,则BC的长为( )
A. B. C. D.
6.如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D从点A出发以每秒1cm的速度向点C运动,当点D运动到线段AB的中垂线与线段AC的交点处时,运动时间是( )
A.秒 B.秒 C.秒 D.秒
【考点4】勾股定理 面积
7.在中,,,,的对边分别是a,b,c,若,,则的面积是( )
A. B. C. D.
8.如图,在Rt△ABC中,∠BCA=90°,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )
A.2 B.4 C.6 D.9
【考点5】勾股定理 网格问题
9.如图,在2×2正方形网格中,以格点为顶点的的面积等于,则点A到边的距离为( )
A. B. C.2 D.
10.如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:①△ACD的面积是有理数;②四边形ABCD的四条边的长度都是无理数;③四边形ABCD的三条边的长度是无理数,一条边的长度是有理数.其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
【考点6】勾股定理 线段的平方和(差)
11.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
12.若直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,则有( )
A. B.+= C.+= D.
【考点7】勾股定理的逆定理 判定三角形的形状
13.学校的书香苑呈三角形形状,三边分别是9,12,15,那么书香苑的面积是( )
A.135 B.180 C.108 D.54
14.已知a、b、c是三角形的三边长,若满足,则这个三角形的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.直角三角形
【考点8】勾股定理的逆定理 弦图问题
15.我国清代数学家李锐借助三个正方形用出入相补的方法证明了勾股定理.如图,设直角三角形两直角边的长分别为a、b(),斜边的长为c.作三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使E、F、G三点在一条直线上,若,四边形与面积之和为13.5,则正方形的面积为( )
A.32 B.36 C.46 D.49
16.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,若,大正方形面积为15,则小正方形面积为( )
A.3 B.4 C.6 D.12
【考点9】勾股定理的逆定理 勾股定理与无理数
17.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,,若以点A为圆心,的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为( )
A. B. C. D.
18.如图,O为数轴的原点,数轴上点A、B表示的数分别是1和2,CA⊥OA于点A,且AC=OA;DB⊥OB于点B,且DB=OA;以点O为圆心,OC长为半径画弧,交数轴于点E;以点O为圆心,OD长为半径画弧,交数轴于点F;则点E和点F表示的数分别是()
A.1.4,2.2 B. C. D.
【考点10】勾股定理的逆定理 勾股定理的证明方法
19.如图,在四边形中,,,点C是边上一点,,..下列结论;①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.5 B.4 C.3 D.2
20.下面图形能够验证勾股定理的有( )
A.4个 B.3个 C.2个 D.1个
【考点11】勾股定理的逆定理 用勾股定理构造图形解决问题
21.平面内,将长分别为2,4,3的三根木棒按如图方式连接成折线,其中可以绕点任意旋转,保持,将,两点用绷直的皮筋连接,设皮筋长度为,则不可能是( )
A.3 B.5 C.7 D.8
22.《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绸索,绳索从木柱上端顺木桂下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部9尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为( )
A. B.
C. D.
【考点12】勾股定理的逆定理 用勾股定理与折叠问题
23.如图,在,,,沿过点A的直线折叠,使点B落在边上的点D处,再次折叠,使点C与点D重合,折痕交于点E,则的长度为( )
A. B. C. D.
24.如图,将一张正方形纸片对折,使与重合,得到折痕后展开,E为上一点,将沿所在的直线折叠,使得点C落在折痕上的点F处,连接.若,则的长度为( )
A. B. C. D.
二、填空题
【考点1】勾股定理 勾股数
25.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑥组勾股数为 .
26.勾股定理本身就是一个关于,,的方程,满足这个方程的正整数解常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:,,,…,分析上面勾股数组可以发现,,,,…分析上面规律,第6个勾股数组为 .
【考点2】勾股定理 勾股树
27.如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13,则图中所有的正方形的面积之和为 .
28.如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的面积为40,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x+y= .
【考点3】勾股定理 求线段长
29.定义:如图,点P、Q把线段AB分割成线段AP、PQ和BQ,若以AP、PQ、BQ为边的三角形是一个直角三角形,则称点P、Q是线段AB的勾股分割点.已知点P、Q是线段AB的勾股分割点,如果AP=8,PQ=12(PQ>BQ),那么BQ= .
30.如图1,点,为边长为8cm的正方形边,上的动点,连接,点为边的中点.将正方形沿线段折叠,使点的对应点落在线段上,点的对应点为,如图2所示.则线段的取值范围是 .
【考点4】勾股定理 面积
31.如图所示,四边形ADEF为正方形,ABC为等腰直角三角形,D在BC边上,△ABC的面积等于98,BD:DC=2:5,则正方形ADEF的面积等于 .
32.在中,,边上的高为15,则的面积是 .
【考点5】勾股定理 网格问题
33.如图,将放在每个小正方形的边长为1的网格中,点均落在格点上.
(1)的面积等于________.
(2)请在如图所示的网格中,用无刻度的直尺,过点画一条直线,交于点,使的面积等于面积的3倍,并简要说明画图的方法__________.(不要求证明)
34.如图,在每个小正方形的边长为1的网格中,A,B为格点在如图所示的网格中求作一点C,使得且的面积等于,则此时的长为 .
【考点6】勾股定理 线段的平方和(差)
35.如图,已知,直角中,,从直角三角形两个锐角顶点所引的中线的长,,则斜边AB之长为 .
36.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形,对角线交于点,若,则 .
【考点7】勾股定理的逆定理 判定三角形的形状
37.有一块土地的形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,则这块土地的面积为 .
38.已知三角形的三边长之比为,则此三角形的形状是 .
【考点8】勾股定理的逆定理 弦图问题
39.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若,大正方形的面积为,则的长为 .
40.如图1,将长为,宽为的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到两个正方形.
(1)图2中小正方形的边长为___________(用含的代数式表示):
(2)当时,该大正方形的面积是___________.
【考点9】勾股定理的逆定理 勾股定理与无理数
41.如图,矩形的边在数轴上,其中点A,B分别表示数,2,,以点B为圆心,长为半径作弧交数轴于点P,则点P表示的数为 .
42.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2022个等腰直角三角形的斜边长是 .
【考点10】勾股定理的逆定理 勾股定理的证明方法
43.如图所示的正方形图案是用4个全等的直角三角形拼成的.已知正方形的面积为25,正方形的面积为1,若用、分别表示直角三角形的两直角边,下列三个结论:①;②;③;④.其中正确的是 (填序号).
44.如图,两个边长分别为a,b,c的直角三角形和一个两条直角边长都是的直角三角形拼成如图形状用不同的方法计算这个图形的面积,可得关于a,b,c的一个等式是 .
【考点11】勾股定理的逆定理 用勾股定理构造图形解决问题
45.如图, 是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为,面积是25的正方形的四个顶点分别在这四条直线上,那么的值是 .
46.已知,在中,,高,则边长为 .
【考点12】勾股定理的逆定理 用勾股定理与折叠问题
47.已知中,,,,将它的一条直角边沿一锐角角平分线所在直线翻折,使直角顶点落在斜边上,则折叠后不重合部分三角形的面积为 .
48.如图,三角形纸片,点是边上一点,连接,把沿着翻折,得到,与交于点,连接交于点若,,,的面积为,则点到的距离为 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据勾股定理即可解答.
【详解】A、,则不构成勾股数,故本选项不符合题意.
B、,则不构成勾股数,故本选项不符合题意.
C、,则不构成勾股数,故本选项不符合题意.
D、,构成勾股数,故本选项符合题意.
故选:D.
【点睛】本题考查了勾股数,熟练掌握勾股定理是解题的关键.
2.B
【分析】由表格中的数据得:,,即可求出的值.
【详解】解:由表格中的数据得:,,
,
当时,,
.
故选:.
【点睛】本题考查了勾股数,掌握表中数据的变化规律,找到数据的关系是解答本题的关键.
3.C
【分析】根据正方形的面积公式,结合勾股定理,能够导出正方形A,B,C,D的面积和即为最大正方形的面积.
【详解】解:如下图:
根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,
S1=42+62,S2=32+42,
于是S3=S1+S2,
即可得S3=16+36+9+16=77.
故选:C.
【点睛】本题考查了勾股定理的知识,根据勾股定理的几何意义表示出S3是解答本题的关键.
4.C
【分析】根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
【详解】解:∵OP=1,,,
同理:,
∴,
故选:C .
【点睛】本题考查了勾股定理的应用,解此题的关键是能根据求出的结果得出规律.
5.B
【分析】由勾股定理求出AD=2,则AC=AE=AD﹣DE=2﹣2,得BC=AB﹣AC=6﹣2即可.
【详解】解:∵BD⊥AB,,BD=2,
∴AB=4,
∴AD===2,
∵DE=BD=2,
∴AC=AE=AD﹣DE=2﹣2,
∴BC=AB﹣AC=4﹣(2﹣2)=6﹣2;
故选:B.
【点睛】本题考查勾股定理,掌握勾股定理是解题的关键.
6.B
【分析】画出图形,根据勾股定理解答即可.
【详解】如图所示:
中,,,,
,
是的中垂线,
,
连接,
,
在中,,
即,
解得:,
当点运动到的中垂线与线段AC的交点时,运动时间为秒.
故选.
【点睛】此题考查勾股定理的应用,线段垂直平分线的性质,关键是根据勾股定理构建直角三角形进行解答.
7.A
【分析】根据题意可知,的面积为,结合已知条件,根据完全平方公式变形求值即可.
【详解】解:中,,,,所对的边分别为a,b,c,
,
∵,,
∴,
,故A正确.
故选:A.
【点睛】本题主要考查了勾股定理,完全平方公式变形求值,解题的关键是将完全平方公式变形求出ab的值.
8.A
【分析】根据勾股定理可求AC2+BC2=AB2,再根据三角形的面积公式即可求解.
【详解】解:在Rt△ABC中,∠BCA=90°,
∴AC2+BC2=AB2,
∴AC2+BC2=AB2,
∵△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,
∴△ACH的面积是10﹣8=2.
故选:A.
【点睛】本题考查勾股定理,熟知勾股定理是解题的关键.
9.B
【分析】根据勾股定理计算出的长,再根据三角形的面积,即可求出点A到边的距离.
【详解】解:设点A到边的距离为h,
∵,,
∴,
∴点A到边的距离为,
故选B.
【点睛】本题主要考查了勾股定理的应用,掌握面积法是关键.
10.C
【详解】①∵△ACD的面积=×2×3=3,
∴①说法正确;
②∵CD=2,
∴说法②错误;
③由勾股定理得:AB=,
∴说法③正确;
正确的说法有2个.
故选C.
11.D
【分析】在Rt△ABD及Rt△ADC中可分别表示出BD2及CD2,在Rt△BDM及Rt△CDM中分别将BD2及CD2的表示形式代入表示出BM2和MC2,然后作差即可得出结果.
【详解】解:在Rt△ABD和Rt△ADC中,
BD2=AB2 AD2,CD2=AC2 AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2 AD2+MD2,MC2=CD2+MD2=AC2 AD2+MD2,
∴MC2 MB2=(AC2 AD2+MD2) (AB2 AD2+MD2)
=AC2 AB2
=45.
故选:D.
【点睛】本题考查了勾股定理的知识,题目有一定的技巧性,比较新颖,解答本题需要认真观察,分别两次运用勾股定理求出MC2和MB2是本题的难点,重点还是在于勾股定理的熟练掌握.
12.C
【分析】根据三角形的面积求法,可将斜边的高h用两直角边表示出来.
【详解】∵直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,
∵ab=ch,
∴h=,
∴,
∴+===.
故选C.
【点睛】本题主要考查勾股定理以及三角形的面积公式,根据勾股定理结合三角形的面积公式,进行适当的变形,是解题的关键.
13.D
【详解】试题解析:∵在△ABC中,三条边的长度分别为9、12、15,92+122=152,
∴△ABC是直角三角形,
∴书香苑的面积是.
故选D.
14.D
【分析】首先根据绝对值,平方数与算术平方根的非负性,求出a,b,c的值,在根据勾股定理的逆定理判断其形状是直角三角形.
【详解】∵(a-6)2≥0,≥0,|c-10|≥0,
∴a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴这个三角形是直角三角形.
故选D.
【点睛】本题主要考查了非负数的性质与勾股定理的逆定理,此类题目在考试中经常出现,是考试的重点.
15.B
【分析】证明≌,得到,再证明≌,从而推出,化简得到,再根据,得到,结合两式可得,从而计算结果.
【详解】解:在与中,
,
∴≌(HL),
∴,
∴,
又∵,
∴,
∴,
在与中,
,
∴≌(ASA),
∴
,
∴,
即,
化简得:①,
又∵,
∴,
∴②,
,得:,
∴.
故选B.
【点睛】本题考查了勾股定理,全等三角形的判定和性质,解题的关键是证明三角形全等,根据图形面积得到相应等式,从而进行计算.
16.A
【分析】观察图形可知,小正方形的面积=大正方形的面积减去4个直角三角形的面积,利用已知,大正方形的面积为15,可以得出4个直角三角形的面积,进而求出答案.
【详解】解:∵,
∴,
∵直角三角形的较长直角边长为a,较短直角边长为b,
∴大正方形的边长为.
∵大正方形的面积为15,
∴,
∴
∴,
∴小正方形的面积为.
故选:A.
【点睛】此题考查了完全平方公式,以及勾股定理的应用,熟练应用勾股定理是解题关键.
17.B
【详解】根据勾股定理得:,,
∴,
∴,
∴点表示的数为.
故答案为:B.
【点睛】此题主要考查了勾股定理,以及数轴与实数,解题时求数轴上两点间的距离应让较大的数减去较小的数即可,本题的关键是求出AE的长.
18.B
【解析】根据勾股定理及数轴性质解答 .
【详解】解:由题意可得:
,
,
∴点E和点F表示的数分别是,
故选B.
【点睛】本题考查勾股定理及数轴的综合应用,熟练掌握勾股定理的应用及用数轴表示数的方法是解题关键.
19.C
【分析】证明,由全等三角形的性质可得出,.再由图形的面积可得出①②⑤正确.
【详解】解:,,
,
.
在和中,
,
,
,.
,
.
,
,
故①②正确;
,,
四边形的面积是;
故③错误;
梯形的面积直角三角形的面积两个直角三角形的面积,
,
,,
故④错误,故⑤正确
故①②⑤共3个正确,③④错误.
故选:C.
【点睛】本题考查了全等三角形的判定及性质的运用,勾股定理的证明,垂直的判定及性质的运用,解答时证明三角形全等是关键.
20.A
【分析】分别计算图形的面积进行证明即可.
【详解】解:第一个图:由,可得,故该项的图形能够验证勾股定理;
第二个图:由,可得,故该项的图形能够验证勾股定理;
第三个图:由,可得,故该项的图形能够验证勾股定理;
第四个图:由,可得,故该项的图形能够验证勾股定理;
故选:A.
【点睛】此题考查了图形与勾股定理的推导,熟记勾股定理的计算公式及各种图形面积的计算方法是解题的关键.
21.D
【分析】连接,根据勾股定理可得的长,在分两种情况讨论即可;
【详解】连接,则.
如图1,当点在线段上时,;
如图2,当点在的延长线上时,,
∴的取值范围为,
故选:D.
【点睛】本题主要考查了勾股定理的应用、三角形的三边关系,解题的关键是构造直角三角形,利用勾股定理求出.
22.C
【分析】设绳索长为x尺,根据勾股定理列出方程解答即可.
【详解】解:设绳索长为x尺,可列方程为,
故选:C.
【点睛】本题考查了由实际问题抽象出方程,勾股定理的应用,找准等量关系,正确列出方程是解题的关键.
23.B
【分析】根据题意可得,,,,可得,继而设,则,根据勾股定理即可求解.
【详解】解:∵沿过点A的直线将纸片折叠,使点B落在边上的点D处,
∴,,
∵折叠纸片,使点C与点D重合,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得,
即,
故选:B
【点睛】本题考查了折叠的性质,勾股定理,掌握折叠的性质以及勾股定理是解题的关键.
24.A
【分析】由正方形可得,再由折叠可得,,,,利用勾股定理可求的长,进而得到,在中,利用勾股定理构造方程,即可求得的长.
【详解】解:∵四边形是正方形
∴
由折叠可得,,,
故选:A.
【点睛】本题只要考查折叠问题中勾股定理的运用,在这类问题中利用勾股定理构造方程是常用的方法.
25.16,63,65
【分析】据前面的几组数可以得到每组勾股数与各组的序号之间的关系,如果是第n组数,则这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1.根据这个规律即可解答.
【详解】解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1,
故可得第⑥组勾股数是16,63,65.
故答案为选:16,63,65.
【点睛】本题考查了勾股数,此题属规律性题目,解答此题的关键是根据所给的勾股数找出规律,按照此规律即可解答.
26.13,84,85
【分析】由勾股数组:(3,4,5),(5,12,13),(7,24,25)…中,4=1×(3+1),12=2×(5+1),24=3×(7+1),…可得第6组勾股数中间的数为6×(13+1)=84,进而得出(13,84,85).
【详解】解:∵第1组:3=2×1+1,4=1×(3+1),5=4+1;
第2组:5=2×2+1,12=2×(5+1),13=12+1;
第3组:7=2×3+1,24=3×(7+1),25=24+1;
∴第n组:2n+1,n(2n+1+1),n(2n+1+1)+1,
∴第6组:2×6+1=13,6×(13+1)=84,84+1=5.
故答案为:13,84,85.
【点睛】本题考查的是勾股数的规律探究,能够根据题意找到每组勾股数之间的关系是解决本题的关键.
27.507
【分析】根据勾股定理有S正方形2+S正方形3=S正方形1,S正方形C+S正方形D=S正方形3,S正方形A+S正方形B=S正方形2,等量代换即可求所有正方形的面积之和.
【详解】解:如图所示,
根据勾股定理可知,
S正方形2+S正方形3=S正方形1,
S正方形C+S正方形D=S正方形3,
S正方形A+S正方形B=S正方形2,
∴S正方形C+S正方形D+S正方形A+S正方形B
=S正方形2+S正方形3
=S正方形1,
则S正方形1+正方形2+S正方形3+S正方形C+S正方形D+S正方形A+S正方形B
=3S正方形1
=3×132
=3×169
=507.
故答案为507
【点睛】本题考查了勾股定理.有一定难度,注意掌握直角三角形中,两直角边的平方和等于斜边的平方.
28.22
【分析】如图,先表示出正方形B的面积,继而观察图形得出正方形A、B的面积差,列式整理即可求得答案.
【详解】如图,由图可看出,正方形B的面积等于10+x,
正方形A与正方形B的面积的差等于8+y,
又正方形A的面积为40,
所以8+y=40-(10+x),
所以x+y=22,
故答案为22.
【点睛】此题结合正方形的面积公式以及勾股定理发现各正方形的面积之间的关系,正确把握和灵活运用相关知识是解题的关键.
29.4
【分析】由题干中勾股分割点的定义可得:AP2+BQ2=PQ2,据此即可解答.
【详解】解:由题意可得,AP2+BQ2=PQ2,即82+BQ2=122,解得BQ=4,
故答案为4.
【点睛】本题考查了勾股定理的运用,理解题意并确定三条线段谁是直角边、谁是斜边是解题关键.
30.
【分析】当点P 与点B 重合时,CN 取得最小值0;当点P 与点E 重合时,CN 取得最大值,根据正方形边长为8,点为边的中点,设CN=x,则,CE=4,根据,利用勾股定理即可得出CN的长,取两种情况的中间值即可得到线段的取值范围.
【详解】当点P 与点B 重合时,CN 取得最小值0;
当点P 与点E 重合时,CN 取得最大值
如图,
正方形边长为8,点为边的中点
设CN=x,则,CE=4
在中,
即
解得
此时,
所以,线段的取值范围是.
故答案为:.
【点睛】本题考查了折叠问题,涉及正方形的性质、勾股定理的应用,熟练掌握知识点是解题的关键.
31.116
【分析】过点A作,交BC于点H,根据等腰直角三角形的性质可得:,利用三角形面积公式可得:,然后根据勾股定理得出:,根据题意BD:DC=2:5,结合,可得,,在中,利用勾股定理可得正方形的边长,根据正方形面积公式即可求出面积.
【详解】解:过点A作,交BC于点H,
∴,
∵等腰直角的面积等于98,
∴,
∴,
又∵BD:DC=2:5,
∴,,
在中,
,
∴正方形ABCD的面积:.
故本题答案为:116.
【点睛】题目主要考查等腰直角三角形的性质、线段比及勾股定理,作出辅助线应用勾股定理是解题关键.
32.或
【分析】分是锐角和是钝角两种情况,进行求解即可.
【详解】解:①当点D在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
②当点D不在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
综上:的面积是或.
【点睛】本题考查勾股定理.解题的关键是画出图形,利用分类讨论的思想进行求解.
33.(1)2
(2)见解析
【分析】(1)根据三角形的面积公式,即可求出答案;
(2)根据题意,在上取,即可画出图形.
【详解】(1)解:;
(2)解:如图:找的四等分点,连接为所求.
作法:①取线段,在线段取一点,使,
②过作的平行线,使,交于点,
③作直线.
则直线就是所求作的直线.
【点睛】本题考查了复杂作图,以及三角形的面积,解题的关键是学会利用分割法求三角形面积,巧妙利用格点作四等分点,属于作图中比较难的题目.
34.
【分析】的面积等于,,确定点C所在的位置,即可求解.
【详解】∵,
∴
∵的面积等于,
∴点C所在的位置如图所示,
∴
故答案为:
【点睛】本题考查勾股定理求三角形线段的长,解题的关键是确定点C所在的位置.
35.8
【分析】设BC=x,AC=y,根据勾股定理列方程组,从而可求得斜边的平方,即求得斜边的长.
【详解】设BC=x,AC=y,
∵直角三角形两个锐角顶点所引的中线
∴
在Rt△ADC和Rt△BCE中,由勾股定理得:
∴
∴
∴
故答案为:8
【点睛】注意此题的解题技巧:根据已知条件,在两个直角三角形中运用勾股定理列方程组.求解的时候,注意不必分别求出未知数的值,只需求出两条直角边的平方和,运用勾股定理即可.
36.136
【分析】在Rt△BOC和Rt△AOD中,根据勾股定理得,, 在Rt△AOB和Rt△COD中,根据勾股定理得,,进一步得,最后求得.
【详解】解:,
,
在Rt△BOC和Rt△AOD中,根据勾股定理得,,
在Rt△AOB和Rt△COD中,根据勾股定理得,,
, ,
;
故答案为:.
【点睛】本题考查勾股定理的应用,熟练掌握勾股定理在实际问题中的应用,从题中抽象出勾股定理这一数学模型是解题关键.
37.234m2
【分析】连接AC,则△ABC和△ACD均为直角三角形,根据AB,BC可以求出AC,根据AC,CD可以求出AD,根据直角三角形面积计算可以求出△ABC和△ACD的面积,四边形ABCD的面积为两个直角三角形面积之和.
【详解】连接AC,
在Rt△ABC中,AC为斜边,
则AC===25(m),
在Rt△ACD中,AC为斜边,则AD==═24(m),
四边形ABCD面积S=AB×BC+AD×CD=×20×15+×7×24=234(m2).
故答案为234m2.
【点睛】本题考查了勾股定理在实际生活中的应用以及直角三角形面积计算,本题中正确的运用勾股定理计算AC是解题的关键.
38.等腰直角三角形
【分析】由已知得其有两条边相等,并且符合勾股定理的逆定理,从而可判断三角形的形状.
【详解】解:由题意设三边长分别为:x,x,x
∴三角形一定为直角三角形,并且是等腰三角形.
故答案为等腰直角三角形.
【点睛】本题考查了勾股定理的逆定理,三角形三边关系满足a2+b2=c2,三角形为直角三角形.
39.
【分析】由题意可知:中间小正方形的边长为:,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.
【详解】由题意可知:中间小正方形的边长为:,
∵大正方形的面积为
∴,
又∵,
∴,
∴,即
∴
故答案为.
【点睛】本题考查了勾股定理的证明,熟练掌握该知识点是本题解题的关键.
40.(1)
(2)17
【分析】(1)观察图形,用直角三角形较长的直角边减去较短的直角边即可;
(2)当时,求出大正方形的边长即可求其面积.
【详解】(1)解:∵直角三角形较短的直角边,
较长的直角边,
∴小正方形的边长;
故答案为:;
(2)解:当时,大正方形的边长,
∴大正方形的面积.
故答案为:17
【点睛】本题考查了列代数式,代数式求值,观察图形,用直角三角形较长的直角边减去较短的直角边求出小正方形的边长是解题的关键.
41.##
【分析】根据勾股定理求出,,再利用数轴上两点间距离即可求出点P.
【详解】解:∵,
∴,
∴,
∴点P表示的数为:.
故答案为:.
【点睛】本题考查了实数与数轴的关系,在数轴上表示无理数,其中利用距离求点是解题的关键.
42.21011
【分析】先根据勾股定理计算第1个,第2个,第3个,第4个等腰直角三角形的斜边长,找到规律后即可求出第2022个等腰直角三角形的斜边长.
【详解】根据勾股定理可得
第1个Rt△ABC的斜边AC=;
第2个Rt△ACD的斜边AD=;
第3个Rt△ADE的斜边AE=;
第4个Rt△AEF的斜边AF=;
......
第n个等腰直角三角形的斜边=;
∴第2022个等腰直角三角形的斜边=.
【点睛】本题考查了勾股定理及找规律求等腰直角三角形的斜边长,找到规律是解题的关键.
43.①②③
【分析】用含有的代数式分别表示小正方形及大正方形的边长,然后根据面积关系得出与的关系式,依次判断所给关系式即可.
【详解】解:由题意可得小正方形的边长=1,大正方形的边长=5,
斜边2=大正方形的面积,
故①正确;
∵小正方形的边长为1,
,
故②正确;
∵小正方形的面积+四个直角三角形的面积等于大正方形的面积,
,
,
故③正确;
,
故④不正确.
综上可得①②③正确.
故答案为:①②③.
【点睛】本题考查了勾股定理的证明,完全平方公式的变形应用等知识,根据所给图形,利用面积关系判断与的关系是解答本题的关键.
44.
【分析】用两种方法求图形面积,一是直接利用梯形面积公式来求;一是利用三个三角形面积之和来求.
【详解】根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b) =ab+ab+c2,即(a+b)(a+b) =ab+ab+c2,
整理得:a2+b2=c2.
故答案为:a2+b2=c2.
【点睛】本题考查了勾股定理的证明,整式的混合运算,熟练掌握运算法则是解本题的关键.
45.
【分析】过点作构造全等三角形,利用全等三角形的性质得到关于正方形面积的方程,然后解方程求解即可.
【详解】解:过点作交于点,交于点,
在正方形中,
又
∵正方形的面积为25,
或(舍去)
故答案为:
【点睛】本题主要考查全等三角形及勾股定理和正方形面积的关系,通过辅助线构造全等三角形并利用勾股定理列方程是解决本题的关键.
46.7或5
【分析】根据题意画出符合条件的图形,分别考虑当高AD在内部和外部的情况,再用勾股定理求解.
【详解】
如图:当AD在△ABC内部时,
∵,,
∴,,
∴BC=6+1=7;
如图:当AD在△ABC外部时,
∵,,
∴,,
∴BC=6-1=5;
故答案为:7或5
【点睛】本题主要考查了用勾股定理求三角形的边,熟练地掌握勾股定理的内容,根据题意进行分类讨论是解题的关键.
47.或6
【分析】首先利用勾股定理求出的斜边的长,然后根据题意,分两种情况画出图形,利用折叠的性质和勾股定理求解即可.
【详解】解:在中,,,,
∴,
可分两种情况:
第一种情况:如图1,不重合部分是,
∵直角边沿的平分线所在直线翻折,直角顶点C落在斜边上点D处,
∴,,,
∴,
设,则,
∴,即,
解得,
∴,
∴;
第二种情况:如图2,不重合部分是,
∵直角边沿的平分线所在直线翻折,直角顶点C落在斜边上点D处,
∴,,
∴,
设,则,
∴,即,
解得,
∴,
∴;
综上所述,折叠后不重合部分三角形的面积为或6.
故答案为:或6.
【点睛】本题是几何变换综合题,考查了勾股定理、折叠的性质的知识.根据题意分情况计算是解答本题的关键.
48.
【分析】先求出的面积.根据三角形的面积公式求出,设点到的距离为,根据,求出即可解决问题.
【详解】解:,
,
,
由翻折可知,≌,,
,,
,
,
,
,
设点到的距离为,则有,
,
故答案为:.
【点睛】本题考查翻折变换的性质,三角形的面积,勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数构建方程解决问题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
