2023--2024学年苏科版七年级数学上册 6.1线段、射线、直线 课件 17张PPT
文档属性
| 名称 | 2023--2024学年苏科版七年级数学上册 6.1线段、射线、直线 课件 17张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
苏科版 七年级上册
6.1 线段、射线、直线(2)
教学目标:
1. 理解两点确定一直线的事实,理解线段中点的含义
2. 会画一条线段等于已知线段,会求线段的长度
3.通过小组合作、组间竞争等形式,培养学生的团结合作精神,增强学生进取意识,激发他们良好的数学学习情感。
动手画一画
1.在平面上画一个点,过这个点可以画几条直线?
2.在平面上画两个点,过这两个点可以画几条直线?
3.过平面上三点中的每两点画直线,可画多少条直线?
两点确定一条直线
当三点在同一条直线上时,可画一条直线,
当三点不在同一条直线上时,可画三条直线
议一议
下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?
善于分析的同学就会发现,上面问题的实质是比较两条线段的长短,那么怎样比较两条线段的长短呢
●
●
A
B
●
●
C
D
新知探究
●
●
A
B
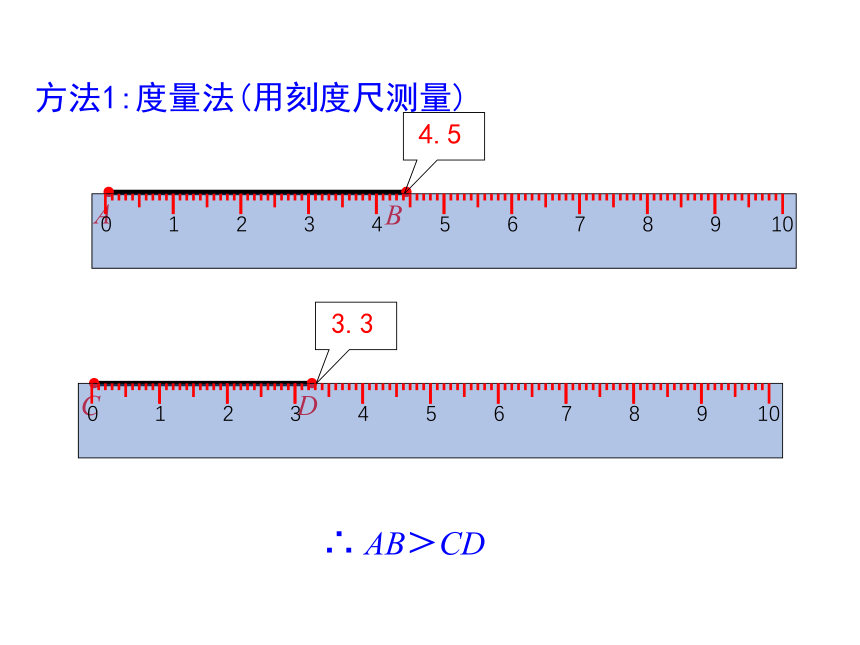
4.5
●
●
C
D
3.3
方法1:度量法(用刻度尺测量)
∴ AB>CD
1
3
2
8
7
4
9
6
5
0
10
1
3
2
8
7
4
9
6
5
0
10
●
●
A
B
●
●
C
D
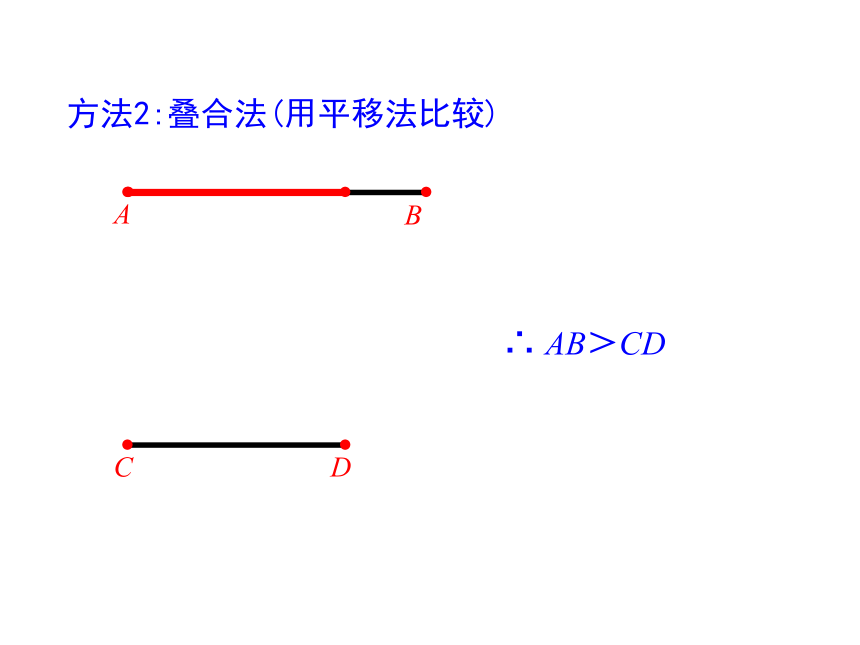
方法2:叠合法(用平移法比较)
●
●
∴ AB>CD
A
B
A
B
A
B
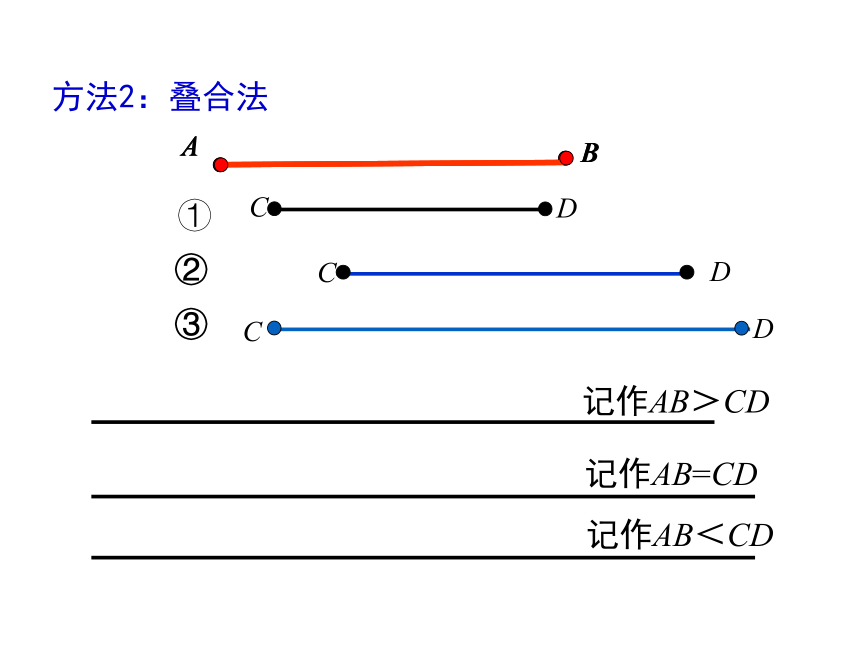
方法2:叠合法
①
②
③
记作AB>CD
记作AB=CD
记作AB<CD
C
D
C
D
C
D
已知线段AB,请用圆规、直尺作一条线段等于已知线段.
A B
做法:1、用直尺作一条射线A′C′.
2、以A′为圆心,在射线A′C′上截取A′B′=AB.
∴线段A′B′就是所求做的线段.
(用圆规量出已知线段AB的长度,在射线A′C′上,以点A′为圆心,以AB长为半径画弧,交射线A′C′ 于点B′,即截取A′B′=AB.)
A′
C′
B′
用尺规作图的方法可以将一条线段移到另一条线段上.
做一做
如图,已知两点A、B
(1)画线段AB;(也可说成连结AB)
.
A
.
B
(2)延长线段AB到点C,使得BC=AB
思考:
1.点A点B点C在同一条直线上吗?
2.线段AB、BC、AC之间有怎样的数量关系?
A
C
B
如图点B把线段AC分成相等的两条线段AB与BC, 点B叫做线段AC的中点.
反过来:如果 AB=BC= AC ,
那么点 B是线段AC的中点.
表达式:如果点B是线段AC的中点,
那么AB=BC= AC.
线段中点
例1 如图,线段AB=8cm,点C是AB的中点,点D在CB上,且DB=1.5cm,求线段CD的长度.
.
.
.
.
A
C
D
B
解:∵C是线段AB的中点
∴CB= AB=4cm
CD=CB-DB
=2.5cm
例题探究
例2、已知线段AB=8cm,直线AB上有一点C,且BC=4cm,M是线段AC的中点,求AM的长。
例题探究
检测反馈:
1.(1分) 下列各种图形中,可以比较大小的是( )
A.两条射线 B.两条直线 C.直线和射线 D.两条线段
2.(1分)已知点C是线段AB上的一点,不能确定C是AB的中点的条件是( )
A.AC=CB B.AC= AB
C.AB=2CB D.AC+CB=AB
3.(2分)如图线段AB=12cm,C是AB的中点,点D在CB上,DB=5cm, 求线段CD的长度.
4.(3分)C为线段AB的中点,D在线段CB上,DA=6,DB=4,求CD的长度.
课堂小结:
1.线段的两种比较方法:
2.线段的中点的概念及表示方法.
∵ 点B是线段AC的中点
∴ AB = BC= AC
或者AC=2AB=2BC
A
C
B
叠合法和度量法.
作业:
1、课本:习题6.1 第6,7,8题
2、完成补充习题
谢 谢!
苏科版 七年级上册
6.1 线段、射线、直线(2)
教学目标:
1. 理解两点确定一直线的事实,理解线段中点的含义
2. 会画一条线段等于已知线段,会求线段的长度
3.通过小组合作、组间竞争等形式,培养学生的团结合作精神,增强学生进取意识,激发他们良好的数学学习情感。
动手画一画
1.在平面上画一个点,过这个点可以画几条直线?
2.在平面上画两个点,过这两个点可以画几条直线?
3.过平面上三点中的每两点画直线,可画多少条直线?
两点确定一条直线
当三点在同一条直线上时,可画一条直线,
当三点不在同一条直线上时,可画三条直线
议一议
下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?
善于分析的同学就会发现,上面问题的实质是比较两条线段的长短,那么怎样比较两条线段的长短呢
●
●
A
B
●
●
C
D
新知探究
●
●
A
B
4.5
●
●
C
D
3.3
方法1:度量法(用刻度尺测量)
∴ AB>CD
1
3
2
8
7
4
9
6
5
0
10
1
3
2
8
7
4
9
6
5
0
10
●
●
A
B
●
●
C
D
方法2:叠合法(用平移法比较)
●
●
∴ AB>CD
A
B
A
B
A
B
方法2:叠合法
①
②
③
记作AB>CD
记作AB=CD
记作AB<CD
C
D
C
D
C
D
已知线段AB,请用圆规、直尺作一条线段等于已知线段.
A B
做法:1、用直尺作一条射线A′C′.
2、以A′为圆心,在射线A′C′上截取A′B′=AB.
∴线段A′B′就是所求做的线段.
(用圆规量出已知线段AB的长度,在射线A′C′上,以点A′为圆心,以AB长为半径画弧,交射线A′C′ 于点B′,即截取A′B′=AB.)
A′
C′
B′
用尺规作图的方法可以将一条线段移到另一条线段上.
做一做
如图,已知两点A、B
(1)画线段AB;(也可说成连结AB)
.
A
.
B
(2)延长线段AB到点C,使得BC=AB
思考:
1.点A点B点C在同一条直线上吗?
2.线段AB、BC、AC之间有怎样的数量关系?
A
C
B
如图点B把线段AC分成相等的两条线段AB与BC, 点B叫做线段AC的中点.
反过来:如果 AB=BC= AC ,
那么点 B是线段AC的中点.
表达式:如果点B是线段AC的中点,
那么AB=BC= AC.
线段中点
例1 如图,线段AB=8cm,点C是AB的中点,点D在CB上,且DB=1.5cm,求线段CD的长度.
.
.
.
.
A
C
D
B
解:∵C是线段AB的中点
∴CB= AB=4cm
CD=CB-DB
=2.5cm
例题探究
例2、已知线段AB=8cm,直线AB上有一点C,且BC=4cm,M是线段AC的中点,求AM的长。
例题探究
检测反馈:
1.(1分) 下列各种图形中,可以比较大小的是( )
A.两条射线 B.两条直线 C.直线和射线 D.两条线段
2.(1分)已知点C是线段AB上的一点,不能确定C是AB的中点的条件是( )
A.AC=CB B.AC= AB
C.AB=2CB D.AC+CB=AB
3.(2分)如图线段AB=12cm,C是AB的中点,点D在CB上,DB=5cm, 求线段CD的长度.
4.(3分)C为线段AB的中点,D在线段CB上,DA=6,DB=4,求CD的长度.
课堂小结:
1.线段的两种比较方法:
2.线段的中点的概念及表示方法.
∵ 点B是线段AC的中点
∴ AB = BC= AC
或者AC=2AB=2BC
A
C
B
叠合法和度量法.
作业:
1、课本:习题6.1 第6,7,8题
2、完成补充习题
谢 谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
