2023-2024学年度北师大版数学八年级上册第三章 位置与坐标 测试卷(含答案)
文档属性
| 名称 | 2023-2024学年度北师大版数学八年级上册第三章 位置与坐标 测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 215.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 20:52:41 | ||
图片预览


文档简介
第三章测试卷 位置与坐标
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.上海是世界知名的金融中心,以下能准确表示上海市地理位置的是( )
A.在中国的东南方 B.东经121.5°
C.在中国的长江出海口 D.东经121°29′,北纬31°14′
2. 在平面直角坐标系中,点P(-3,a2+1)所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 若点A(a,-1)与点B(2,b)关于y轴对称,则a-b的值是( )
A.-1 B.-3 C.1 D.2
4.如果点A(m,n)在第三象限,那么点B(0,m+n)在( )
A.x轴正半轴上 B.x轴负半轴上 C.y轴正半轴上 D.y轴负半轴上
5. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( )
A.狐狸 B.猫 C.蜜蜂 D.牛
6.如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
A.(-2,2) B.(-2,12) C.(3,7) D.(-7,7)
7.在平面直角坐标系中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(-a,5) B.(a,-5) C.(-a+2,5) D.(-a+4,5)
8.若点M(x,y)的坐标满足x2-y2=0,则点M的位置( )
A.在坐标轴夹角的平分线上 B.在第二、四象限坐标轴夹角的平分线上
C.在第一、三象限坐标轴夹角的平分线上 D.在坐标轴上
9.如图,在平面直角坐标系中,△ABC顶点A,B的坐标分别是(0,4),(0,-2),BC=AC=5,则顶点C的坐标为( )
A.(1,4) B.(4,1) C.(4,2) D.(3,1)
10.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2023秒时,点P的坐标是( )
A.(2023,0) B. (2023,-1) C.(2023,1) D.(2024,0)
二、填空题(每小题3分,共15分)
11. 点A(-3,2)关于x轴对称的点的坐标为__ _.
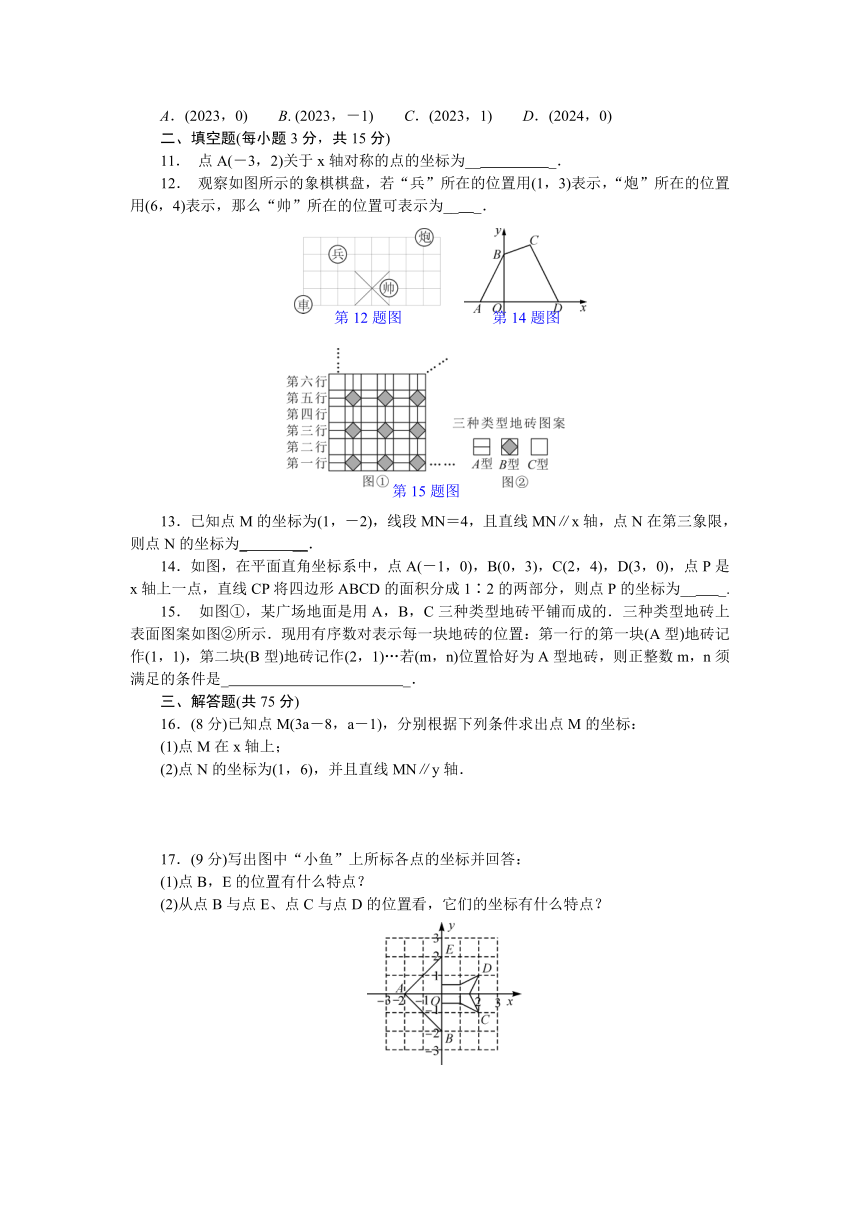
12. 观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为__ _.
13.已知点M的坐标为(1,-2),线段MN=4,且直线MN∥x轴,点N在第三象限,则点N的坐标为_ __.
14.如图,在平面直角坐标系中,点A(-1,0),B(0,3),C(2,4),D(3,0),点P是x轴上一点,直线CP将四边形ABCD的面积分成1∶2的两部分,则点P的坐标为__ _.
15. 如图①,某广场地面是用A,B,C三种类型地砖平铺而成的.三种类型地砖上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块(A型)地砖记作(1,1),第二块(B型)地砖记作(2,1)…若(m,n)位置恰好为A型地砖,则正整数m,n须满足的条件是_ _.
三、解答题(共75分)
16.(8分)已知点M(3a-8,a-1),分别根据下列条件求出点M的坐标:
(1)点M在x轴上;
(2)点N的坐标为(1,6),并且直线MN∥y轴.
17.(9分)写出图中“小鱼”上所标各点的坐标并回答:
(1)点B,E的位置有什么特点?
(2)从点B与点E、点C与点D的位置看,它们的坐标有什么特点?
18.(9分)如图是某台阶的一部分,如果点A的坐标为(0,0),点B的坐标为(1,1).
(1)请建立适当的直角坐标系,并写出C,D,E,F的坐标;
(2)说明B,C,D,E,F的坐标与点A的坐标相比有什么变化?
(3)如果该台阶有10级,你能得到该台阶的高度吗?
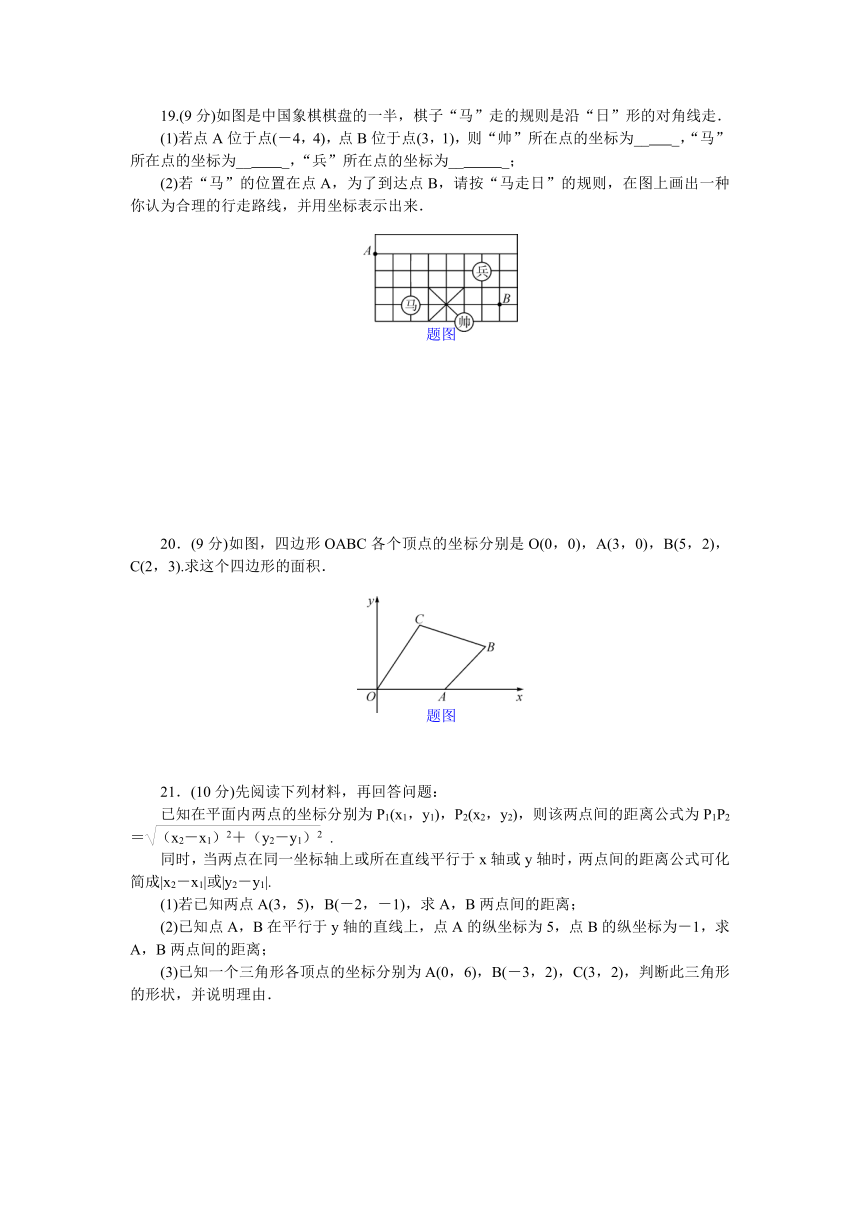
19.(9分)如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.
(1)若点A位于点(-4,4),点B位于点(3,1),则“帅”所在点的坐标为__ _,“马”所在点的坐标为__ _,“兵”所在点的坐标为__ _;
(2)若“马”的位置在点A,为了到达点B,请按“马走日”的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.
20.(9分)如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
21.(10分)先阅读下列材料,再回答问题:
已知在平面内两点的坐标分别为P1(x1,y1),P2(x2,y2),则该两点间的距离公式为P1P2=.
同时,当两点在同一坐标轴上或所在直线平行于x轴或y轴时,两点间的距离公式可化简成|x2-x1|或|y2-y1|.
(1)若已知两点A(3,5),B(-2,-1),求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,求A,B两点间的距离;
(3)已知一个三角形各顶点的坐标分别为A(0,6),B(-3,2),C(3,2),判断此三角形的形状,并说明理由.
22.(10分)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)作出△ABC关于y轴对称的图形△A′B′C′;
(3)在y轴上是否存在一点P,使△ABP的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.(11分)如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1)求△ABC三个顶点A,B,C的坐标;
(2)若点P的坐标为(1,6),连接PA,PB,则△PAB的面积为__2__;
(3)是否存在一点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标.
答案:
第三章 位置与坐标
(时间:100分钟 满分:120分)
( D )
( B )
3.( A )
4.( D )
5.( B )
6.( C )
7.( D )
8.( A )
9.( B )
10.( B )
11.__(-3,-2)__.
12. __(4,1)__.
13.__(-3,-2)__.
14.__(-0.5,0)或(1.25,0)__.
15.__m、n同为奇数或m、n同为偶数__.
16.
解:(1)因为点M在x轴上,所以a-1=0,所以a=1,所以3a-8=-5,所以点M的坐标是(-5,0)
(2)因为直线MN∥y轴,所以3a-8=1,解得a=3,所以a-1=2,所以点M的坐标是(1,2)
17.
解:由图可知,A(-2,0),B(0,-2),C(2,-1),D(2,1),E(0,2).
(1)点B(0,-2)和点E(0,2)关于x轴对称
(2)点B(0,-2)与点E(0,2)、点C(2,-1)与点D(2,1)均关于x轴对称,它们的横坐标相同,纵坐标互为相反数
18.
解:(1)以A点为原点,水平方向为x轴,建立平面直角坐标系,画图略,所以C,D,E,F各点的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5)
(2)B,C,D,E,F的坐标与点A的坐标相比,横坐标与纵坐标分别加1,2,3,4,5
(3)每级台阶高为1,宽也为1,所以10级台阶的高度是10
(1)若点A位于点(-4,4),点B位于点(3,1),则“帅”所在点的坐标为__(1,0)__,“马”所在点的坐标为__(-2,1)__,“兵”所在点的坐标为__(2,3)__;
(2)若“马”的位置在点A,为了到达点B,请按“马走日”的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.
解:(2)答案不唯一,如:路线如图所示,用坐标表示为A(-4,4)→(-2,3)→(0,2)→(2,3)→B(3,1)
20.
解:分别过C点和点B作CF⊥y轴于点F,BH⊥x轴于点H,再分别延长FC,HB交于点E,如图,则E(5,3),所以S四边形ABCO=S长方形OHEF-S△ABH-S△CBE-S△OCF=5×3-×2×2-×1×3-×3×2=
21.
解:(1)AB==
(2)AB=|-1-5|=6
(3)△ABC为等腰三角形,理由如下:因为AB==5,BC==6,AC==5,所以AB=AC,所以△ABC为等腰三角形
22.
解:(1)点B的坐标为(2,0)或(-4,0),画图略
(2)图略
(3)设点P到x轴的距离为h,则×3h=10,解得h=.当点P在y轴的正半轴上时,P(0,);当点P在y轴的负半轴上时,P(0,-).综上所述,存在一点P,使△ABP的面积为10,此时点P的坐标为(0,)或(0,-)
23.(1)求△ABC三个顶点A,B,C的坐标;
(2)若点P的坐标为(1,6),连接PA,PB,则△PAB的面积为__2__;
(3)是否存在一点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标.
解:(1)因为S△ABO=OA·OB,OA=OB,所以OA2=8,解得OA=4,所以OB=OA=4,所以OC=BC-OB=12-4=8,所以A(0,4),B(-4,0),C(8,0)
(3)存在,理由如下:S△ABC=×4×12=24,当点P在第一象限,即a>0时,过点P作PH⊥x轴于点H,①当0<a≤2时,则S△PAB=S△PBH-(S△AOB+S梯形AOHP),即×6(a+4)-(a+8)=24,解得a=-10,不合题意,舍去;②当a>2时,则S△PAB=S△AOB+S梯形AOHP-S△PBH=8+a-×6(a+4)=24,解得a=14,所以此时点P的坐标为(14,6);当点P在第二象限,即a<0时,过点P作PG⊥y轴于点G,则S△PAB=S梯形OBPG-S△APG-S△OAB,即-(-a)-8=24,解得a=-10,所以此时点P的坐标为(-10,6).综上所述,点P的坐标为(-10,6)或(14,6)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.上海是世界知名的金融中心,以下能准确表示上海市地理位置的是( )
A.在中国的东南方 B.东经121.5°
C.在中国的长江出海口 D.东经121°29′,北纬31°14′
2. 在平面直角坐标系中,点P(-3,a2+1)所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 若点A(a,-1)与点B(2,b)关于y轴对称,则a-b的值是( )
A.-1 B.-3 C.1 D.2
4.如果点A(m,n)在第三象限,那么点B(0,m+n)在( )
A.x轴正半轴上 B.x轴负半轴上 C.y轴正半轴上 D.y轴负半轴上
5. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( )
A.狐狸 B.猫 C.蜜蜂 D.牛
6.如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
A.(-2,2) B.(-2,12) C.(3,7) D.(-7,7)
7.在平面直角坐标系中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(-a,5) B.(a,-5) C.(-a+2,5) D.(-a+4,5)
8.若点M(x,y)的坐标满足x2-y2=0,则点M的位置( )
A.在坐标轴夹角的平分线上 B.在第二、四象限坐标轴夹角的平分线上
C.在第一、三象限坐标轴夹角的平分线上 D.在坐标轴上
9.如图,在平面直角坐标系中,△ABC顶点A,B的坐标分别是(0,4),(0,-2),BC=AC=5,则顶点C的坐标为( )
A.(1,4) B.(4,1) C.(4,2) D.(3,1)
10.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2023秒时,点P的坐标是( )
A.(2023,0) B. (2023,-1) C.(2023,1) D.(2024,0)
二、填空题(每小题3分,共15分)
11. 点A(-3,2)关于x轴对称的点的坐标为__ _.
12. 观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为__ _.
13.已知点M的坐标为(1,-2),线段MN=4,且直线MN∥x轴,点N在第三象限,则点N的坐标为_ __.
14.如图,在平面直角坐标系中,点A(-1,0),B(0,3),C(2,4),D(3,0),点P是x轴上一点,直线CP将四边形ABCD的面积分成1∶2的两部分,则点P的坐标为__ _.
15. 如图①,某广场地面是用A,B,C三种类型地砖平铺而成的.三种类型地砖上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块(A型)地砖记作(1,1),第二块(B型)地砖记作(2,1)…若(m,n)位置恰好为A型地砖,则正整数m,n须满足的条件是_ _.
三、解答题(共75分)
16.(8分)已知点M(3a-8,a-1),分别根据下列条件求出点M的坐标:
(1)点M在x轴上;
(2)点N的坐标为(1,6),并且直线MN∥y轴.
17.(9分)写出图中“小鱼”上所标各点的坐标并回答:
(1)点B,E的位置有什么特点?
(2)从点B与点E、点C与点D的位置看,它们的坐标有什么特点?
18.(9分)如图是某台阶的一部分,如果点A的坐标为(0,0),点B的坐标为(1,1).
(1)请建立适当的直角坐标系,并写出C,D,E,F的坐标;
(2)说明B,C,D,E,F的坐标与点A的坐标相比有什么变化?
(3)如果该台阶有10级,你能得到该台阶的高度吗?
19.(9分)如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.
(1)若点A位于点(-4,4),点B位于点(3,1),则“帅”所在点的坐标为__ _,“马”所在点的坐标为__ _,“兵”所在点的坐标为__ _;
(2)若“马”的位置在点A,为了到达点B,请按“马走日”的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.
20.(9分)如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
21.(10分)先阅读下列材料,再回答问题:
已知在平面内两点的坐标分别为P1(x1,y1),P2(x2,y2),则该两点间的距离公式为P1P2=.
同时,当两点在同一坐标轴上或所在直线平行于x轴或y轴时,两点间的距离公式可化简成|x2-x1|或|y2-y1|.
(1)若已知两点A(3,5),B(-2,-1),求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,求A,B两点间的距离;
(3)已知一个三角形各顶点的坐标分别为A(0,6),B(-3,2),C(3,2),判断此三角形的形状,并说明理由.
22.(10分)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)作出△ABC关于y轴对称的图形△A′B′C′;
(3)在y轴上是否存在一点P,使△ABP的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
23.(11分)如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1)求△ABC三个顶点A,B,C的坐标;
(2)若点P的坐标为(1,6),连接PA,PB,则△PAB的面积为__2__;
(3)是否存在一点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标.
答案:
第三章 位置与坐标
(时间:100分钟 满分:120分)
( D )
( B )
3.( A )
4.( D )
5.( B )
6.( C )
7.( D )
8.( A )
9.( B )
10.( B )
11.__(-3,-2)__.
12. __(4,1)__.
13.__(-3,-2)__.
14.__(-0.5,0)或(1.25,0)__.
15.__m、n同为奇数或m、n同为偶数__.
16.
解:(1)因为点M在x轴上,所以a-1=0,所以a=1,所以3a-8=-5,所以点M的坐标是(-5,0)
(2)因为直线MN∥y轴,所以3a-8=1,解得a=3,所以a-1=2,所以点M的坐标是(1,2)
17.
解:由图可知,A(-2,0),B(0,-2),C(2,-1),D(2,1),E(0,2).
(1)点B(0,-2)和点E(0,2)关于x轴对称
(2)点B(0,-2)与点E(0,2)、点C(2,-1)与点D(2,1)均关于x轴对称,它们的横坐标相同,纵坐标互为相反数
18.
解:(1)以A点为原点,水平方向为x轴,建立平面直角坐标系,画图略,所以C,D,E,F各点的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5)
(2)B,C,D,E,F的坐标与点A的坐标相比,横坐标与纵坐标分别加1,2,3,4,5
(3)每级台阶高为1,宽也为1,所以10级台阶的高度是10
(1)若点A位于点(-4,4),点B位于点(3,1),则“帅”所在点的坐标为__(1,0)__,“马”所在点的坐标为__(-2,1)__,“兵”所在点的坐标为__(2,3)__;
(2)若“马”的位置在点A,为了到达点B,请按“马走日”的规则,在图上画出一种你认为合理的行走路线,并用坐标表示出来.
解:(2)答案不唯一,如:路线如图所示,用坐标表示为A(-4,4)→(-2,3)→(0,2)→(2,3)→B(3,1)
20.
解:分别过C点和点B作CF⊥y轴于点F,BH⊥x轴于点H,再分别延长FC,HB交于点E,如图,则E(5,3),所以S四边形ABCO=S长方形OHEF-S△ABH-S△CBE-S△OCF=5×3-×2×2-×1×3-×3×2=
21.
解:(1)AB==
(2)AB=|-1-5|=6
(3)△ABC为等腰三角形,理由如下:因为AB==5,BC==6,AC==5,所以AB=AC,所以△ABC为等腰三角形
22.
解:(1)点B的坐标为(2,0)或(-4,0),画图略
(2)图略
(3)设点P到x轴的距离为h,则×3h=10,解得h=.当点P在y轴的正半轴上时,P(0,);当点P在y轴的负半轴上时,P(0,-).综上所述,存在一点P,使△ABP的面积为10,此时点P的坐标为(0,)或(0,-)
23.(1)求△ABC三个顶点A,B,C的坐标;
(2)若点P的坐标为(1,6),连接PA,PB,则△PAB的面积为__2__;
(3)是否存在一点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标.
解:(1)因为S△ABO=OA·OB,OA=OB,所以OA2=8,解得OA=4,所以OB=OA=4,所以OC=BC-OB=12-4=8,所以A(0,4),B(-4,0),C(8,0)
(3)存在,理由如下:S△ABC=×4×12=24,当点P在第一象限,即a>0时,过点P作PH⊥x轴于点H,①当0<a≤2时,则S△PAB=S△PBH-(S△AOB+S梯形AOHP),即×6(a+4)-(a+8)=24,解得a=-10,不合题意,舍去;②当a>2时,则S△PAB=S△AOB+S梯形AOHP-S△PBH=8+a-×6(a+4)=24,解得a=14,所以此时点P的坐标为(14,6);当点P在第二象限,即a<0时,过点P作PG⊥y轴于点G,则S△PAB=S梯形OBPG-S△APG-S△OAB,即-(-a)-8=24,解得a=-10,所以此时点P的坐标为(-10,6).综上所述,点P的坐标为(-10,6)或(14,6)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
