六年级下册沪教版长方体的再认识复习学案
图片预览



文档简介
长方体的再认识
教学目标 认识长方体的顶点、棱、面等元素。会画长方体的直观图。熟练掌握长方体中的棱与棱的位置关系,棱与面的位置关系,面与面的位置关系。知道一些简单的检验方法。会求长方体的表面积和体积。
教学重难点 重点:长方体的概念、画法,长方体中棱、面之间的位置关系。难点:利用工具检验空间直线、平面之间的位置关系。
长方体的元素
1、长方体有___个面,___个顶点,______条棱。长方体的____________叫做长方体的元素。
2、长方体的特征:
(1)长方体的每个面__________________;
(2)长方体的十二条棱______________________________________________________;
(3)长方体的六个面________________________________________________________。
3、从长方体同一顶点出发的三条棱分别代表了长方体的___________________。
4、当__________________时,长方体变成正方体。
【例题精选】
例1、用一根长度为100厘米的塑料管要做一个长10厘米,宽8厘米,高6厘米的长方体架子,这根塑料管的长度足够吗?需要怎样截取?
例2、要做一个棱长分别为6厘米、14.5 ( http: / / www.21cnjy.com )厘米的、8厘米的无盖的纸盒,至少需要硬纸板多少平方厘米?(接缝处忽略不计)这个纸盒的容积是多少立方厘米?
例3、一个长方体中,有公共点的三条棱的长度 ( http: / / www.21cnjy.com )的比为2:3:4,最小的一个面的面积为216cm2,(1)求这个长方体所有棱长的总和;(2)求这个长方体的表面积;(3)求这个长方体的体积。
例4、一个正方体平均切成8个小正方体后,表面积增加30厘米2。原正方体的表面积是多少?
例5、把一个长9dm,宽6dm,高3dm的 ( http: / / www.21cnjy.com )长方体,分割成完全一样的三个小长方体,试求三个小长方体表面积之和比原长方体的表面积增加多少dm2
长方体直观图的画法
1、平面的画法:平面可以用 ( http: / / www.21cnjy.com )一个__________来表示。把________的平面画成一边是水平位置,另一边与________所成的角为_______的平行四边形。
2、画长方体直观图一般采用________画法。
3、画一个长为2cm、宽为1.6cm、高为2.5cm的长方体,如图所示:
第一步:画平行四边形ABCD,使__________________________________;
第二步:过A、B分别画AB的________________,过C、D分别画CD的________________,且________________。
第三步:顺次连结EFGH;第四步:将被遮住的线段改成______表示。
【例题精选】
例1、画一个长宽高分别是5cm、4cm、3cm的长方体;画一个棱长总和为36厘米的正方体;
例2、画一个长方体,使它一个顶点出发的三条棱长分别是a、b、c.
例3、把下列长方体画完整。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
长方体中棱与棱的位置关系
1、空间两直线的位置关系:________________________
(1)如果直线AB与CD___________________________,那么称这两条直线的位置关系为相交,
(2) 如果直线AB与CD__________________________,那么称这两条直线的位置关系为平行.
(3) 如果直线AB与CD__________________________,那么称这两条直线的位置关系为异面.
2、长方体中棱与棱的位置关系:______________________;
3、在长方体中,与某一条棱相交的棱 ( http: / / www.21cnjy.com )有_____条,则有______对相交的棱;与某一条棱平行的棱有_____条,则有_____对平行的棱;与某一条棱异面的棱有_____条,则有_____对异面的棱。
【例题精选】
例1、如图,在长方体ABCD-EFGH中,
与棱AE平行的棱是____________________
与棱AE相交的棱是____________________
与棱AE异面的棱是____________________;与棱BE平行的棱是____________________
与棱BE相交的棱是____________________;与棱BE异面的棱是____________________
上图中,共有________对没有公共点的棱。
例2、如图所示,一张长方形纸片ABCD对折后翻开所成的图形。
试问:(1)与直线BE平行的直线有_______________
(2)与直线EF相交的直线有_________________________
(3)图中异面的直线有____对,分别是________________
______________________________________
长方体中棱与面的位置关系
1、长方体中棱与平面的位置关系:______________________;
2、在长方体中,与一条棱垂直的平面 ( http: / / www.21cnjy.com )有_____个,与一个面垂直的棱有_____条。与一条棱平行的平面有_____个,与一个平面平行的棱有______条。
3、检验一条直线与平面垂直的方法有_______________________________________
4、检验一条直线与平面平行的方法有_______________________________________
【例题精选】
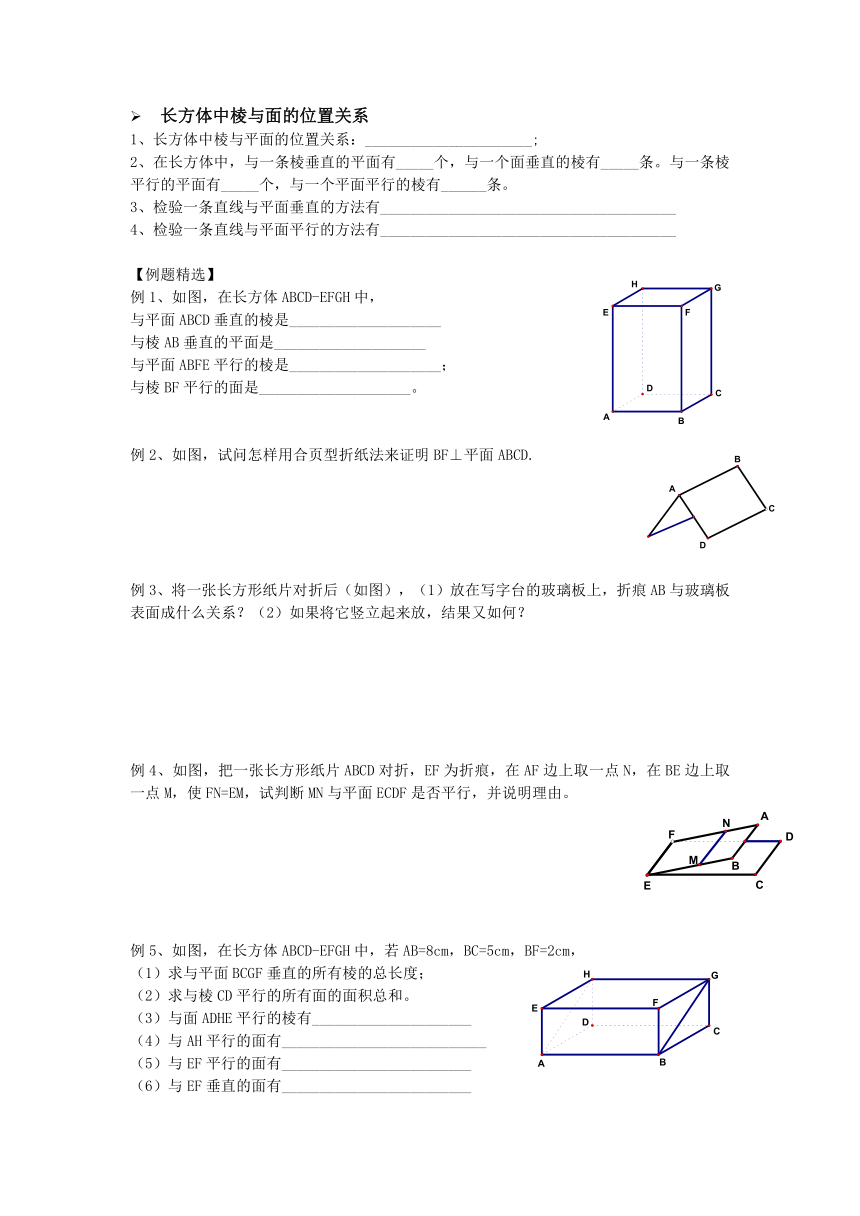
例1、如图,在长方体ABCD-EFGH中,
与平面ABCD垂直的棱是____________________
与棱AB垂直的平面是____________________
与平面ABFE平行的棱是____________________;
与棱BF平行的面是____________________。
例2、如图,试问怎样用合页型折纸法来证明BF⊥平面ABCD.
例3、将一张长方形纸片对折后(如图),(1)放在写字台的玻璃板上,折痕AB与玻璃板表面成什么关系?(2)如果将它竖立起来放,结果又如何?
例4、如图,把一张长方形纸片ABCD对折,E ( http: / / www.21cnjy.com )F为折痕,在AF边上取一点N,在BE边上取一点M,使FN=EM,试判断MN与平面ECDF是否平行,并说明理由。
例5、如图,在长方体ABCD-EFGH中,若AB=8cm,BC=5cm,BF=2cm,
(1)求与平面BCGF垂直的所有棱的总长度;
(2)求与棱CD平行的所有面的面积总和。
(3)与面ADHE平行的棱有_____________________
(4)与AH平行的面有___________________________
(5)与EF平行的面有_________________________
(6)与EF垂直的面有_________________________
(7)与面ABGH平行的棱有_____________________
长方体中面与面的位置关系
1、长方体中平面与平面的位置关系:______________________;
2、在长方体中,与一个面垂 ( http: / / www.21cnjy.com )直的平面有_____个,则有_____对互相垂直的面;与一个面平行的平面有_____个,则有______对互相平行的面。
3、检验一条平面与平面垂直的方法有_______________________________________
4、检验一条平面与平面平行的方法有_______________________________________
【例题精选】
例、如图,在长方体ABCD-EFGH中,
与平面ABCD垂直的面是____________________
与平面ABFE平行的面是____________________;
与平面ABGH垂直的面是____________________。
【练习】
1.如图,长方体中,与面CDD1C1垂直的棱有____ _____.
2.如图,长方体中,与面BCC1B1垂直的面有_____ _____.
3.如图,在长方体中,与面CDD1C1平行的棱有_____ __.
4.如图,沿长方形ABC ( http: / / www.21cnjy.com )D的对角线BD与长方形A1B1C1D1的对角线B1D1将长方体截成相等的两部分,截面BDD1B1,是一个______形,与它平行的棱有__________.
5.如图,将一张长方形的硬纸片对折,张开一个角度,然后直立于平面ABCD上,那么折痕MN与平面ABCD的关系是 .
6.如图,对长方体如图所示那样截去一角后余下的几何体有_________个顶点,_______条棱,________个面.
7.如图所示,长方体截去两个角的几何体 ( http: / / www.21cnjy.com ),剩下有 个顶点, 条棱, 个面.
8.如图是长方体的 六面展开图,在原来长方体中,与平面B垂直的面有_______.
9.如图,是由棱长为1的小正方体构成,其小正方体的个数为 个.
10. 如图,将一个横截面是正方形(面 ( http: / / www.21cnjy.com )BCGF)的长方体木料,沿平面AEGC分割成大小相同的两块,表面积增加了30平方厘米.已知EG长5厘米,分割后每块木料的体积是18立方厘米.求原来这块长方体木料的表面积是多少?
课外作业
一.选择题(每题4分,共24分)
1.长方体裁12条棱中,棱相等的至少有 ( ).
(A) 2条; (B) 4条; (C) 6条; (D) 8条.
2.在长方体中,与一条棱垂直的平面有 ( ).
(A) 1个; (B )2个 ; (C) 3个; (D) 4个.
3.在长方体中,与一个平面垂直的棱有 ( ).
(A)1个; (B)2个; (C)3个; (D)4个.
4.以下说法中正确的个数是 ( ).
(1)水平面是平面,但平面不一定是水平面;
(2)凡与铅垂线重合的直线一定垂直于平面;
(3)直立于桌面上的合页型折纸的折痕必垂直于桌面;
(4)如果长方体的两条棱没有公共点,那么它们一定平行.
(A)1个; (B)2个; (C)3个; (D)4个.
5.下面哪个不是检验直线与平面垂直的工具 ( ).
(A)铅垂线; (B)长方形纸片; (C)三角尺; (D)合页型折纸.
6.长方体中,相邻的两个平面 ( ).
(A)有垂直关系; (B)有平行关系; (C)可能垂直也可能平行; (D)无法确定.
二、填空:(每小题4分,共48分)
7.空间两条直线的位置关系有__________________.
8.长方体的长是12cm,宽是8cm,高是5cm,这个长方体所有的棱长和是_______.
9.如图,在山坡上栽种的小树,要检验它是否与地平面垂直,应该用什么方法检验:____________________________.
10.如图,长方体中,与面CDD1C1垂直的棱有____ _____.
11.如图,长方体中,与面BCC1B1垂直的面有_____ _____.
12.如图,在长方体中,与面CDD1C1平行的棱有_____ __.
13.如图,沿长方形ABCD的对角 ( http: / / www.21cnjy.com )线BD与长方形A1B1C1D1的对角线B1D1将长方体截成相等的两部分,截面BDD1B1,是一个______形,与它平行的棱有__________.
14.如图,将一张长方形的硬纸片对折,张 ( http: / / www.21cnjy.com )开一个角度,然后直立于平面ABCD上,那么折痕MN与平面ABCD的关系是 .
15.如图,对长方体如图所示那样截去一角后余下的几何体有_________个顶点,_______条棱,________个面.
16.如图所示,长方体截去两个角的几 ( http: / / www.21cnjy.com )何体,剩下有 个顶点, 条棱, 个面. 17.如图是长方体的 六面展开图,在原来长方体中,与平面B 垂直的面有_______.
18.如图,是由棱长为1的小正方体构成 ( http: / / www.21cnjy.com ),其小正方体的个数为 个.
三.作图题(12分+14分,共26分)
19.画一个长方体,使它一个顶点出发的三条棱长分别是a、b、c.
20.补画下面的图形,使之成为长方体的直观图.
四、简答题(12分+12分+14分+14分,共52分)
21.用一根108cm长的铁丝做一个长、宽、高的比为2:3:4的长方体框,那么这个长方体的体积是多少?
22.把长、宽、高分别为5㎝、4㎝、3㎝两个相同的长方体粘合成一个大的长方体,求大长方体的表面积和体积.
23.如图,将一个横截面是正方 ( http: / / www.21cnjy.com )形(面BCGF)的长方体木料,沿平面AEGC分割成大小相同的两块,表面积增加了30平方厘米.已知EG长5厘米,分割后每块木料的体积是18立方厘米.求原来这块长方体木料的表面积是多少?
24.小明准备用透明胶和硬纸板制作一个长方体纸盒,现在需要你的帮忙:
(1)制作前,要画出长方体纸盒的直观图,小明只画了一部分(如图1),请你帮他画完整(不写画法);
(2)制作时,需要裁剪一块长方形的硬纸板,小明经过设计发现正好将这块硬纸板全部用完(如图2),请你求出长方体的长、宽和高;
(3)制作完成后,小明想把这个盒子表面的其中5个面都涂满相同的颜色,而且要使涂色部分的面积最少,那么涂色部分的面积是多少呢?
图1 图2
教学目标 认识长方体的顶点、棱、面等元素。会画长方体的直观图。熟练掌握长方体中的棱与棱的位置关系,棱与面的位置关系,面与面的位置关系。知道一些简单的检验方法。会求长方体的表面积和体积。
教学重难点 重点:长方体的概念、画法,长方体中棱、面之间的位置关系。难点:利用工具检验空间直线、平面之间的位置关系。
长方体的元素
1、长方体有___个面,___个顶点,______条棱。长方体的____________叫做长方体的元素。
2、长方体的特征:
(1)长方体的每个面__________________;
(2)长方体的十二条棱______________________________________________________;
(3)长方体的六个面________________________________________________________。
3、从长方体同一顶点出发的三条棱分别代表了长方体的___________________。
4、当__________________时,长方体变成正方体。
【例题精选】
例1、用一根长度为100厘米的塑料管要做一个长10厘米,宽8厘米,高6厘米的长方体架子,这根塑料管的长度足够吗?需要怎样截取?
例2、要做一个棱长分别为6厘米、14.5 ( http: / / www.21cnjy.com )厘米的、8厘米的无盖的纸盒,至少需要硬纸板多少平方厘米?(接缝处忽略不计)这个纸盒的容积是多少立方厘米?
例3、一个长方体中,有公共点的三条棱的长度 ( http: / / www.21cnjy.com )的比为2:3:4,最小的一个面的面积为216cm2,(1)求这个长方体所有棱长的总和;(2)求这个长方体的表面积;(3)求这个长方体的体积。
例4、一个正方体平均切成8个小正方体后,表面积增加30厘米2。原正方体的表面积是多少?
例5、把一个长9dm,宽6dm,高3dm的 ( http: / / www.21cnjy.com )长方体,分割成完全一样的三个小长方体,试求三个小长方体表面积之和比原长方体的表面积增加多少dm2
长方体直观图的画法
1、平面的画法:平面可以用 ( http: / / www.21cnjy.com )一个__________来表示。把________的平面画成一边是水平位置,另一边与________所成的角为_______的平行四边形。
2、画长方体直观图一般采用________画法。
3、画一个长为2cm、宽为1.6cm、高为2.5cm的长方体,如图所示:
第一步:画平行四边形ABCD,使__________________________________;
第二步:过A、B分别画AB的________________,过C、D分别画CD的________________,且________________。
第三步:顺次连结EFGH;第四步:将被遮住的线段改成______表示。
【例题精选】
例1、画一个长宽高分别是5cm、4cm、3cm的长方体;画一个棱长总和为36厘米的正方体;
例2、画一个长方体,使它一个顶点出发的三条棱长分别是a、b、c.
例3、把下列长方体画完整。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
长方体中棱与棱的位置关系
1、空间两直线的位置关系:________________________
(1)如果直线AB与CD___________________________,那么称这两条直线的位置关系为相交,
(2) 如果直线AB与CD__________________________,那么称这两条直线的位置关系为平行.
(3) 如果直线AB与CD__________________________,那么称这两条直线的位置关系为异面.
2、长方体中棱与棱的位置关系:______________________;
3、在长方体中,与某一条棱相交的棱 ( http: / / www.21cnjy.com )有_____条,则有______对相交的棱;与某一条棱平行的棱有_____条,则有_____对平行的棱;与某一条棱异面的棱有_____条,则有_____对异面的棱。
【例题精选】
例1、如图,在长方体ABCD-EFGH中,
与棱AE平行的棱是____________________
与棱AE相交的棱是____________________
与棱AE异面的棱是____________________;与棱BE平行的棱是____________________
与棱BE相交的棱是____________________;与棱BE异面的棱是____________________
上图中,共有________对没有公共点的棱。
例2、如图所示,一张长方形纸片ABCD对折后翻开所成的图形。
试问:(1)与直线BE平行的直线有_______________
(2)与直线EF相交的直线有_________________________
(3)图中异面的直线有____对,分别是________________
______________________________________
长方体中棱与面的位置关系
1、长方体中棱与平面的位置关系:______________________;
2、在长方体中,与一条棱垂直的平面 ( http: / / www.21cnjy.com )有_____个,与一个面垂直的棱有_____条。与一条棱平行的平面有_____个,与一个平面平行的棱有______条。
3、检验一条直线与平面垂直的方法有_______________________________________
4、检验一条直线与平面平行的方法有_______________________________________
【例题精选】
例1、如图,在长方体ABCD-EFGH中,
与平面ABCD垂直的棱是____________________
与棱AB垂直的平面是____________________
与平面ABFE平行的棱是____________________;
与棱BF平行的面是____________________。
例2、如图,试问怎样用合页型折纸法来证明BF⊥平面ABCD.
例3、将一张长方形纸片对折后(如图),(1)放在写字台的玻璃板上,折痕AB与玻璃板表面成什么关系?(2)如果将它竖立起来放,结果又如何?
例4、如图,把一张长方形纸片ABCD对折,E ( http: / / www.21cnjy.com )F为折痕,在AF边上取一点N,在BE边上取一点M,使FN=EM,试判断MN与平面ECDF是否平行,并说明理由。
例5、如图,在长方体ABCD-EFGH中,若AB=8cm,BC=5cm,BF=2cm,
(1)求与平面BCGF垂直的所有棱的总长度;
(2)求与棱CD平行的所有面的面积总和。
(3)与面ADHE平行的棱有_____________________
(4)与AH平行的面有___________________________
(5)与EF平行的面有_________________________
(6)与EF垂直的面有_________________________
(7)与面ABGH平行的棱有_____________________
长方体中面与面的位置关系
1、长方体中平面与平面的位置关系:______________________;
2、在长方体中,与一个面垂 ( http: / / www.21cnjy.com )直的平面有_____个,则有_____对互相垂直的面;与一个面平行的平面有_____个,则有______对互相平行的面。
3、检验一条平面与平面垂直的方法有_______________________________________
4、检验一条平面与平面平行的方法有_______________________________________
【例题精选】
例、如图,在长方体ABCD-EFGH中,
与平面ABCD垂直的面是____________________
与平面ABFE平行的面是____________________;
与平面ABGH垂直的面是____________________。
【练习】
1.如图,长方体中,与面CDD1C1垂直的棱有____ _____.
2.如图,长方体中,与面BCC1B1垂直的面有_____ _____.
3.如图,在长方体中,与面CDD1C1平行的棱有_____ __.
4.如图,沿长方形ABC ( http: / / www.21cnjy.com )D的对角线BD与长方形A1B1C1D1的对角线B1D1将长方体截成相等的两部分,截面BDD1B1,是一个______形,与它平行的棱有__________.
5.如图,将一张长方形的硬纸片对折,张开一个角度,然后直立于平面ABCD上,那么折痕MN与平面ABCD的关系是 .
6.如图,对长方体如图所示那样截去一角后余下的几何体有_________个顶点,_______条棱,________个面.
7.如图所示,长方体截去两个角的几何体 ( http: / / www.21cnjy.com ),剩下有 个顶点, 条棱, 个面.
8.如图是长方体的 六面展开图,在原来长方体中,与平面B垂直的面有_______.
9.如图,是由棱长为1的小正方体构成,其小正方体的个数为 个.
10. 如图,将一个横截面是正方形(面 ( http: / / www.21cnjy.com )BCGF)的长方体木料,沿平面AEGC分割成大小相同的两块,表面积增加了30平方厘米.已知EG长5厘米,分割后每块木料的体积是18立方厘米.求原来这块长方体木料的表面积是多少?
课外作业
一.选择题(每题4分,共24分)
1.长方体裁12条棱中,棱相等的至少有 ( ).
(A) 2条; (B) 4条; (C) 6条; (D) 8条.
2.在长方体中,与一条棱垂直的平面有 ( ).
(A) 1个; (B )2个 ; (C) 3个; (D) 4个.
3.在长方体中,与一个平面垂直的棱有 ( ).
(A)1个; (B)2个; (C)3个; (D)4个.
4.以下说法中正确的个数是 ( ).
(1)水平面是平面,但平面不一定是水平面;
(2)凡与铅垂线重合的直线一定垂直于平面;
(3)直立于桌面上的合页型折纸的折痕必垂直于桌面;
(4)如果长方体的两条棱没有公共点,那么它们一定平行.
(A)1个; (B)2个; (C)3个; (D)4个.
5.下面哪个不是检验直线与平面垂直的工具 ( ).
(A)铅垂线; (B)长方形纸片; (C)三角尺; (D)合页型折纸.
6.长方体中,相邻的两个平面 ( ).
(A)有垂直关系; (B)有平行关系; (C)可能垂直也可能平行; (D)无法确定.
二、填空:(每小题4分,共48分)
7.空间两条直线的位置关系有__________________.
8.长方体的长是12cm,宽是8cm,高是5cm,这个长方体所有的棱长和是_______.
9.如图,在山坡上栽种的小树,要检验它是否与地平面垂直,应该用什么方法检验:____________________________.
10.如图,长方体中,与面CDD1C1垂直的棱有____ _____.
11.如图,长方体中,与面BCC1B1垂直的面有_____ _____.
12.如图,在长方体中,与面CDD1C1平行的棱有_____ __.
13.如图,沿长方形ABCD的对角 ( http: / / www.21cnjy.com )线BD与长方形A1B1C1D1的对角线B1D1将长方体截成相等的两部分,截面BDD1B1,是一个______形,与它平行的棱有__________.
14.如图,将一张长方形的硬纸片对折,张 ( http: / / www.21cnjy.com )开一个角度,然后直立于平面ABCD上,那么折痕MN与平面ABCD的关系是 .
15.如图,对长方体如图所示那样截去一角后余下的几何体有_________个顶点,_______条棱,________个面.
16.如图所示,长方体截去两个角的几 ( http: / / www.21cnjy.com )何体,剩下有 个顶点, 条棱, 个面. 17.如图是长方体的 六面展开图,在原来长方体中,与平面B 垂直的面有_______.
18.如图,是由棱长为1的小正方体构成 ( http: / / www.21cnjy.com ),其小正方体的个数为 个.
三.作图题(12分+14分,共26分)
19.画一个长方体,使它一个顶点出发的三条棱长分别是a、b、c.
20.补画下面的图形,使之成为长方体的直观图.
四、简答题(12分+12分+14分+14分,共52分)
21.用一根108cm长的铁丝做一个长、宽、高的比为2:3:4的长方体框,那么这个长方体的体积是多少?
22.把长、宽、高分别为5㎝、4㎝、3㎝两个相同的长方体粘合成一个大的长方体,求大长方体的表面积和体积.
23.如图,将一个横截面是正方 ( http: / / www.21cnjy.com )形(面BCGF)的长方体木料,沿平面AEGC分割成大小相同的两块,表面积增加了30平方厘米.已知EG长5厘米,分割后每块木料的体积是18立方厘米.求原来这块长方体木料的表面积是多少?
24.小明准备用透明胶和硬纸板制作一个长方体纸盒,现在需要你的帮忙:
(1)制作前,要画出长方体纸盒的直观图,小明只画了一部分(如图1),请你帮他画完整(不写画法);
(2)制作时,需要裁剪一块长方形的硬纸板,小明经过设计发现正好将这块硬纸板全部用完(如图2),请你求出长方体的长、宽和高;
(3)制作完成后,小明想把这个盒子表面的其中5个面都涂满相同的颜色,而且要使涂色部分的面积最少,那么涂色部分的面积是多少呢?
图1 图2
