11.1 与三角形有关的线段 同步练习 人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.1 与三角形有关的线段 同步练习 人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 20:01:55 | ||
图片预览


文档简介
第十一章11.1 与三角形有关的线段
2023学年人教版单元同步练习
一、单选题
1.三角形的重心是三角形的( )
A.三条中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三条高所在直线的交点
2.下列四根木棒中,不能与3cm,7cm长的两根木棒钉成一个三角形的是( )
A.4cm B.5cm C.6cm D.7cm
3.如图,在△ABC中,已知S△ABD:S△ACD=2:1,点E是AB的中点,且△ABC的面积为9cm2,则△AED的面积为( )
A.1cm2 B.2cm2 C.3cm2 D.4cm2
4.如果三角形的两条边长分别是8厘米、6厘米,那么第三边的长不可能是( )
A.9厘米 B.4厘米 C.3厘米 D.2厘米
5.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为90( )
A.1 B.2 C.3 D.4
6.如图,为估计池塘岸边A,B两地之间的距离,小明在池塘的一侧选取一点O,测得OA=10米,OB=8米,那么A,B之间的距离可能是( )
A.2米 B.15米 C.18米 D.28米
7.如图,在 ABC中,D是BC上的点,且BD=2,DC=1, =12,那么 等于( )
A.30 B.36 C.72 D.24
8.如下图,将△ABC的各边都延长一倍至A'、B'、C',连接这些点,得到一个新的三角形A'B'C',若△ABC的面积为3,则△A'B'C'的面积是( )
A.18 B.21 C.24 D.3
二、填空题
9.如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2,则△CDE和△BEF的面积分别为 .
10.如图,填空:
由三角形两边的和大于第三边,得
,
.
将不等式左边 右边分别相加,得
,
即 .
11.一个三角形的两边长为8和10,则它的最长边的取值范围是 .
12.如图, 是 的边 上的中线,点 是 的中点,若阴影部分的面积是 ,那么 的面积为 .
13.三角形的三边长分别为3、7、a,且a为偶数,则这个三角形的周长为 .
14.边长为1cm的8个小正方形拼成如图所示的长4cm、宽2cm的长方形。将外围的格点从1号编到12号。最初,点A、B、C分别位于4、8、12号格点上,现以逆时针方向同时移动A、B、C三点,每次各移动到下一个格点,绕了一周回到原先的位置,这过程中,△ABC有 次成为直角三角形;△ABC的面积最大是 cm2。
15.如图,△ABC中,点D、E分别是BC、AD的中点,△ABC的面积为6,则阴影部分的面积是 .
16.一个等腰三角形的两边长分别为5厘米、9厘米,则这个三角形的周长为 .
三、解答题
17.在平面直角坐标系中,O为原点,点.
(1)如图①,则三角形的面积为 ;
(2)如图②,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形的面积;
②点是一动点,若三角形的面积等于三角形的面积.请直接写出点P坐标.
18.如图,AD是的高,CE是的角平分线.若,,求的度数.
19.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.
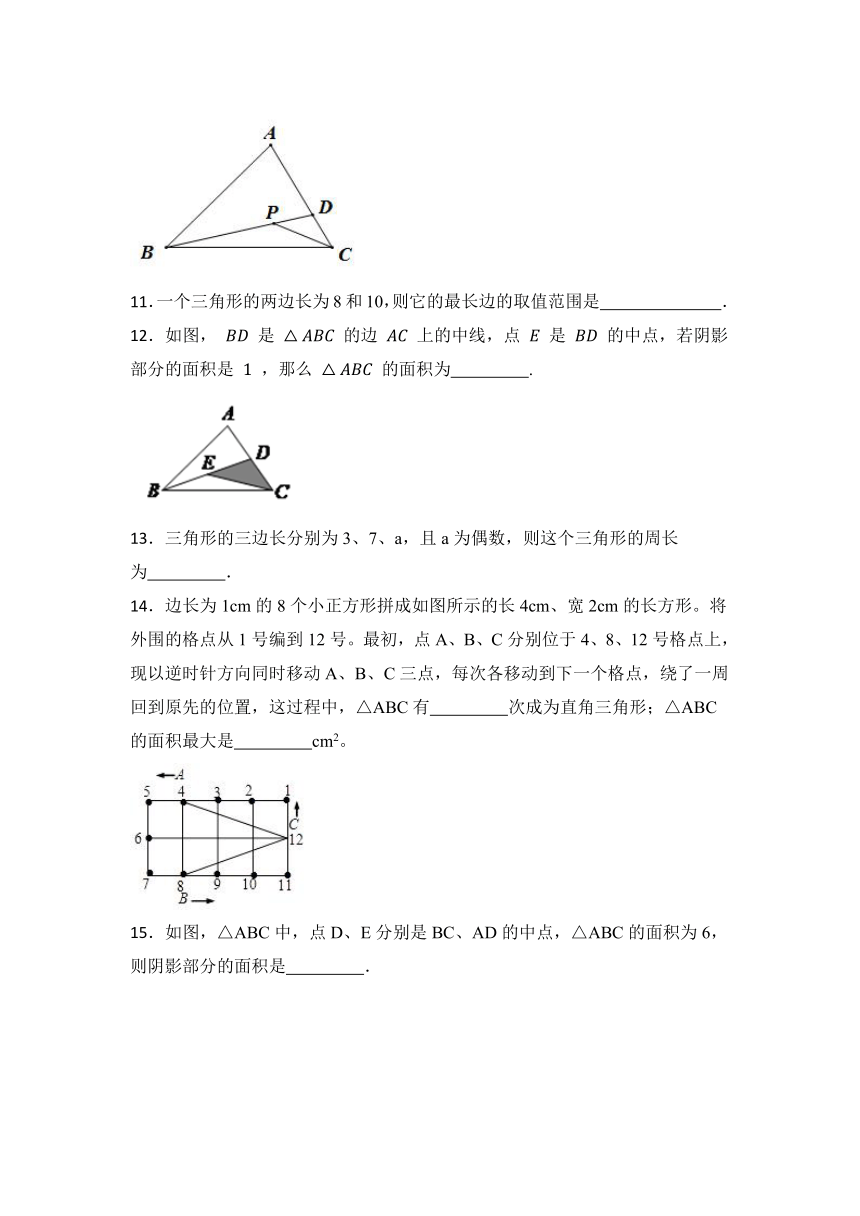
20.已知:如图,P是△ABC内任一点,求证:AB+AC>BP+PC。
答案解析部分
单选题
1.A
2.A
3.C
4.D
5.C
6.B
7.B
8.B
填空题
9.6cm2,5cm2
10.;;;
11.10≤a<18
12.4
13.16或18
14.6;4
15.
16.19厘米或23厘米
解答题
17.(1)6
(2)解:①如图②中由题意,连接.
②或.
18.解:∵AD是的高
∴
∵
∴
∵CE是的角平分线
∴
∵
∴
∴在中,.
19.解:∵点E是AD的中点,
∴S△ABE= S△ABD,S△ACE= S△ADC,
∴S△ABE+S△ACE= S△ABC= ×20=10cm2,
∴S△BCE= S△ABC= ×20=10cm2,
∵点F是CE的中点,
∴S△BEF= S△BCE= ×10=5cm2
20.证明:延长BP交AC于点D,
在△ABD中,PB+PD在△PCD中,PC①+②得PB+PD+PC即PB+PC即:AB+AC>PB+PC.
2023学年人教版单元同步练习
一、单选题
1.三角形的重心是三角形的( )
A.三条中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三条高所在直线的交点
2.下列四根木棒中,不能与3cm,7cm长的两根木棒钉成一个三角形的是( )
A.4cm B.5cm C.6cm D.7cm
3.如图,在△ABC中,已知S△ABD:S△ACD=2:1,点E是AB的中点,且△ABC的面积为9cm2,则△AED的面积为( )
A.1cm2 B.2cm2 C.3cm2 D.4cm2
4.如果三角形的两条边长分别是8厘米、6厘米,那么第三边的长不可能是( )
A.9厘米 B.4厘米 C.3厘米 D.2厘米
5.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为90( )
A.1 B.2 C.3 D.4
6.如图,为估计池塘岸边A,B两地之间的距离,小明在池塘的一侧选取一点O,测得OA=10米,OB=8米,那么A,B之间的距离可能是( )
A.2米 B.15米 C.18米 D.28米
7.如图,在 ABC中,D是BC上的点,且BD=2,DC=1, =12,那么 等于( )
A.30 B.36 C.72 D.24
8.如下图,将△ABC的各边都延长一倍至A'、B'、C',连接这些点,得到一个新的三角形A'B'C',若△ABC的面积为3,则△A'B'C'的面积是( )
A.18 B.21 C.24 D.3
二、填空题
9.如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2,则△CDE和△BEF的面积分别为 .
10.如图,填空:
由三角形两边的和大于第三边,得
,
.
将不等式左边 右边分别相加,得
,
即 .
11.一个三角形的两边长为8和10,则它的最长边的取值范围是 .
12.如图, 是 的边 上的中线,点 是 的中点,若阴影部分的面积是 ,那么 的面积为 .
13.三角形的三边长分别为3、7、a,且a为偶数,则这个三角形的周长为 .
14.边长为1cm的8个小正方形拼成如图所示的长4cm、宽2cm的长方形。将外围的格点从1号编到12号。最初,点A、B、C分别位于4、8、12号格点上,现以逆时针方向同时移动A、B、C三点,每次各移动到下一个格点,绕了一周回到原先的位置,这过程中,△ABC有 次成为直角三角形;△ABC的面积最大是 cm2。
15.如图,△ABC中,点D、E分别是BC、AD的中点,△ABC的面积为6,则阴影部分的面积是 .
16.一个等腰三角形的两边长分别为5厘米、9厘米,则这个三角形的周长为 .
三、解答题
17.在平面直角坐标系中,O为原点,点.
(1)如图①,则三角形的面积为 ;
(2)如图②,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形的面积;
②点是一动点,若三角形的面积等于三角形的面积.请直接写出点P坐标.
18.如图,AD是的高,CE是的角平分线.若,,求的度数.
19.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,求△BEF的面积.
20.已知:如图,P是△ABC内任一点,求证:AB+AC>BP+PC。
答案解析部分
单选题
1.A
2.A
3.C
4.D
5.C
6.B
7.B
8.B
填空题
9.6cm2,5cm2
10.;;;
11.10≤a<18
12.4
13.16或18
14.6;4
15.
16.19厘米或23厘米
解答题
17.(1)6
(2)解:①如图②中由题意,连接.
②或.
18.解:∵AD是的高
∴
∵
∴
∵CE是的角平分线
∴
∵
∴
∴在中,.
19.解:∵点E是AD的中点,
∴S△ABE= S△ABD,S△ACE= S△ADC,
∴S△ABE+S△ACE= S△ABC= ×20=10cm2,
∴S△BCE= S△ABC= ×20=10cm2,
∵点F是CE的中点,
∴S△BEF= S△BCE= ×10=5cm2
20.证明:延长BP交AC于点D,
在△ABD中,PB+PD
