22.3实际问题与二次函数强化训练 人教版数学九年级上册(含答案)
文档属性
| 名称 | 22.3实际问题与二次函数强化训练 人教版数学九年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 784.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 20:14:46 | ||
图片预览



文档简介
22.3实际问题与二次函数
一、单选题
1.一个小球以的初速度向上竖直弹出,它在空中的高度与时间满足关系式,当小球的高度为时,t为( )
A.1s B.2s C.1s或2s D.以上都不对
2.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价每提高2元,则每天少卖4套.设冰墩墩和雪容融套件每套售价定为x元时,则该商品每天销售套件所获利润w与x之间的函数关系式为( ).
A. B.
C. D.
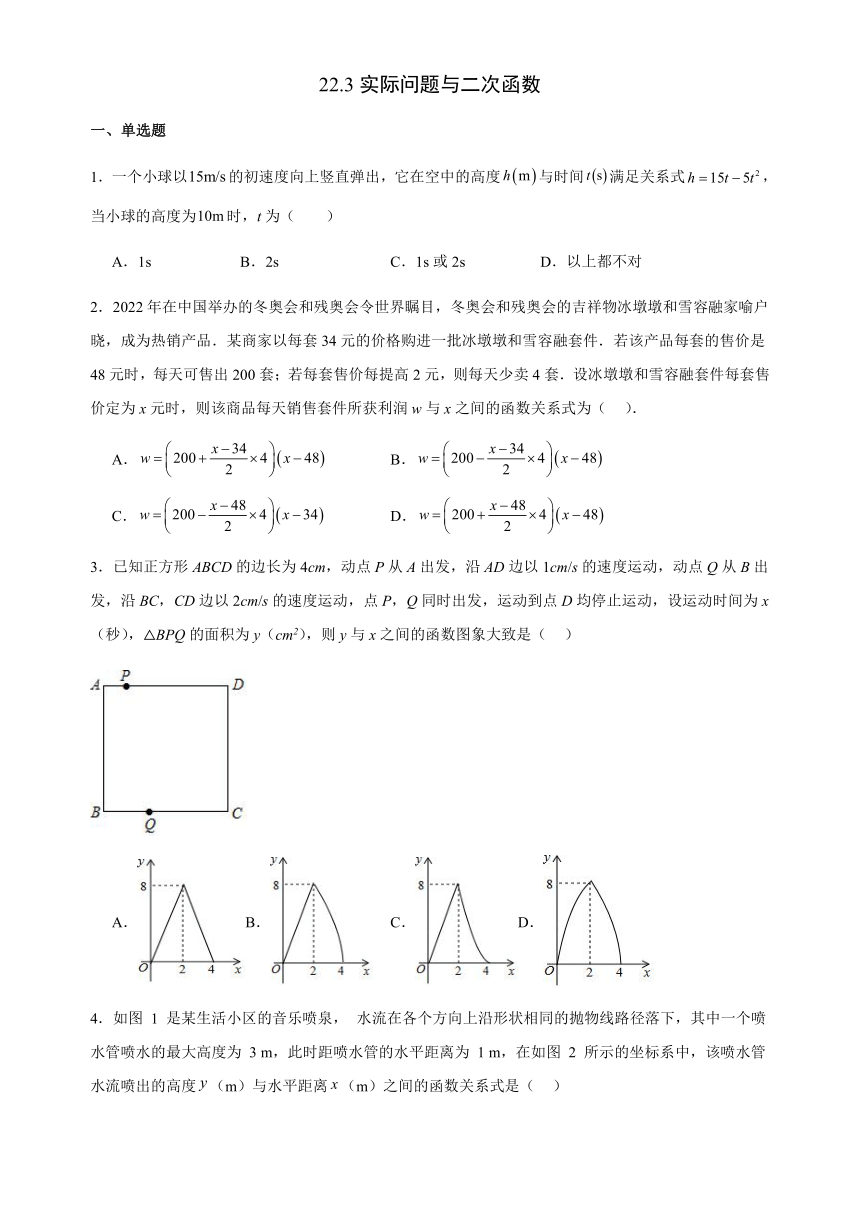
3.已知正方形ABCD的边长为4cm,动点P从A出发,沿AD边以1cm/s的速度运动,动点Q从B出发,沿BC,CD边以2cm/s的速度运动,点P,Q同时出发,运动到点D均停止运动,设运动时间为x(秒),△BPQ的面积为y(cm2),则y与x之间的函数图象大致是( )
A.B. C.D.
4.如图 1 是某生活小区的音乐喷泉, 水流在各个方向上沿形状相同的抛物线路径落下,其中一个喷水管喷水的最大高度为 3 m,此时距喷水管的水平距离为 1 m,在如图 2 所示的坐标系中,该喷水管水流喷出的高度(m)与水平距离(m)之间的函数关系式是( )
A. B.
C. D.
5.18岁的中国选手谷爱凌在北京2022年冬奥会比赛中夺得3枚金牌,被誉为“雪上公主”,谷爱凌从山坡上滑下,其滑行距离(单位:m)与滑行时间(单位:s)之间的关系可以近似地用二次函数刻画,其图像如图所示,根据图像,当滑行时间为时,滑行距离为( )
A.30 B.28.5 C.26.5 D.29
6.现有一块长80cm、宽60cm的矩形钢片,将它的四个角各剪去一个边长为xcm的小正方形,做成一个底面积为ycm2的无盖的长方体盒子,则y与x之间的函数关系式为( )
A.y=x2-70x+1200 B.y=x2-140x+4800 C.y=4x2-280x+4800 D.y=4800-4x2
7.如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.cm2 B.cm2 C.cm2 D.cm2
8.某商场销售的某种商品每件的标价是80元,若按标价的八折销售,仍可盈利24元,市场调查发现:在以标价打八折为销售价的基础上,该种商品每星期可卖出220件,该种商品每降价1元,每星期可多卖20件.设每件商品降价x元(x为整数),每星期的利润为y元.以下说法错误的是( )
A.每件商品进价为40元
B.降价后每件商品售价为元
C.降价后每周可卖件
D.每星期的利润为
9.如图1是太原晋阳湖公园一座抛物线型拱桥,按如图所示建立坐标系,得到函数,在正常水位时水面宽米,当水位上升5米时,则水面宽( )
A.20米 B.15米 C.10米 D.8米
二、填空题
10.设矩形窗户的周长为6m,则窗户面积S(m2)与窗户宽x (m)之间的函数关系式是
11.如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 的值为 .
12.如图,在一面靠墙(墙长不限)的空地上用长为米的篱笆围成中间隔有两道篱笆的矩形鸡场,则所围鸡场最大面积为 平方米.
13.某工厂第一年的利润是20万元,第三年的利润是y万元,与平均年增长率x之间的函数关系式是 .
14.各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为,如果在离水面竖直距离为h(单位:)的地方开大小合适的小孔,那么从小孔射出水的射程s(单位:)与h的关系式为,则射程s最大值是 .(射程是指水流落地点离小孔的水平距离)
15.小亮创办了一个微店商铺,营销一款小型护眼台灯,成本是20元/盏,在“双十一”前20天进行了网上销售后发现,该台灯的日销售量(盏)与时间(天)之间满足一次函数关系,且第1天销售了78盏,第2天销售了76盏,护眼台灯的销售价格(元/盏)与时向(天)之间符合函数关系式(,且为整数).
(1)日销售量(盏)与时间(天)之间的一次函数关系式为 .
(2)这20天中最大日销售利润是 .
三、解答题
16.用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?
17.为响应政府“节能”号召,某强照明公司减少了白炽灯的生产数量,引进新工艺生产一种新型节能灯,已知这种节能灯的出厂价为每个20元.某商场试销发现,销售单价定为25元/个,每月销售量为250个;每涨价1元,每月少卖10个.
(1)求出每月销售量y(个)与销售单价x(元)之间的函数关系式;
(2)设该商场每月销售这种节能灯获得的利润为w(元)与销售单价x(元)之间的函数关系式;
(3)若每月销售量不少于200个,且每个节能灯的销售利润至少为7元,则销售单价定为多少元时,所获利润最大?最大利润是多少?
18.新冠疫情蔓延全球,口罩成了人们的生活必需品,某药店销售普通口罩和N95口罩,今年8月份的进价如下表:
普通口罩 N95口罩
进价(元/包) 8 20
(1)计划N95口罩每包售价比普通口罩贵16元,7包普通口罩和3包N95口罩总售价相同,求普通口罩和N95口罩每包售价;
(2)①按(1)中售价销售一段时间后发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包,该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天的利润为320元,求此时普通口罩每包售价;
②普通口罩售价为多少元时,利润最大?最大利润为多少元?
19.某游乐场的圆形喷水池中心有一雕塑,从点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为轴,点为原点建立直角坐标系,点在轴上,轴上的点、为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为
.
(1)求雕塑高;
(2)求落水点、之间的距离;
(3)若需要在上的点处竖立一尊高3米的雕塑,且,那么雕塑顶部是否会碰到水柱?请通过计算说明.
参考答案:
1.C
2.C
3.B
4.D
5.B
6.C
7.C
8.D
9.A
10.().
11.1+.
12.
13.
14.20
15. 450
16.当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.
17.(1)
(2)
(3)销售单价定为30元时,所获利润最大,最大利润是2000元.
18.(1)普通口罩和 N95 口罩每包售价分别为12元和28元;(2)①10元;②普通口罩售价为11元时,利润最大,最大利润为500元
19.(1)(2)(3)不会碰到水柱
一、单选题
1.一个小球以的初速度向上竖直弹出,它在空中的高度与时间满足关系式,当小球的高度为时,t为( )
A.1s B.2s C.1s或2s D.以上都不对
2.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价每提高2元,则每天少卖4套.设冰墩墩和雪容融套件每套售价定为x元时,则该商品每天销售套件所获利润w与x之间的函数关系式为( ).
A. B.
C. D.
3.已知正方形ABCD的边长为4cm,动点P从A出发,沿AD边以1cm/s的速度运动,动点Q从B出发,沿BC,CD边以2cm/s的速度运动,点P,Q同时出发,运动到点D均停止运动,设运动时间为x(秒),△BPQ的面积为y(cm2),则y与x之间的函数图象大致是( )
A.B. C.D.
4.如图 1 是某生活小区的音乐喷泉, 水流在各个方向上沿形状相同的抛物线路径落下,其中一个喷水管喷水的最大高度为 3 m,此时距喷水管的水平距离为 1 m,在如图 2 所示的坐标系中,该喷水管水流喷出的高度(m)与水平距离(m)之间的函数关系式是( )
A. B.
C. D.
5.18岁的中国选手谷爱凌在北京2022年冬奥会比赛中夺得3枚金牌,被誉为“雪上公主”,谷爱凌从山坡上滑下,其滑行距离(单位:m)与滑行时间(单位:s)之间的关系可以近似地用二次函数刻画,其图像如图所示,根据图像,当滑行时间为时,滑行距离为( )
A.30 B.28.5 C.26.5 D.29
6.现有一块长80cm、宽60cm的矩形钢片,将它的四个角各剪去一个边长为xcm的小正方形,做成一个底面积为ycm2的无盖的长方体盒子,则y与x之间的函数关系式为( )
A.y=x2-70x+1200 B.y=x2-140x+4800 C.y=4x2-280x+4800 D.y=4800-4x2
7.如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.cm2 B.cm2 C.cm2 D.cm2
8.某商场销售的某种商品每件的标价是80元,若按标价的八折销售,仍可盈利24元,市场调查发现:在以标价打八折为销售价的基础上,该种商品每星期可卖出220件,该种商品每降价1元,每星期可多卖20件.设每件商品降价x元(x为整数),每星期的利润为y元.以下说法错误的是( )
A.每件商品进价为40元
B.降价后每件商品售价为元
C.降价后每周可卖件
D.每星期的利润为
9.如图1是太原晋阳湖公园一座抛物线型拱桥,按如图所示建立坐标系,得到函数,在正常水位时水面宽米,当水位上升5米时,则水面宽( )
A.20米 B.15米 C.10米 D.8米
二、填空题
10.设矩形窗户的周长为6m,则窗户面积S(m2)与窗户宽x (m)之间的函数关系式是
11.如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 的值为 .
12.如图,在一面靠墙(墙长不限)的空地上用长为米的篱笆围成中间隔有两道篱笆的矩形鸡场,则所围鸡场最大面积为 平方米.
13.某工厂第一年的利润是20万元,第三年的利润是y万元,与平均年增长率x之间的函数关系式是 .
14.各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为,如果在离水面竖直距离为h(单位:)的地方开大小合适的小孔,那么从小孔射出水的射程s(单位:)与h的关系式为,则射程s最大值是 .(射程是指水流落地点离小孔的水平距离)
15.小亮创办了一个微店商铺,营销一款小型护眼台灯,成本是20元/盏,在“双十一”前20天进行了网上销售后发现,该台灯的日销售量(盏)与时间(天)之间满足一次函数关系,且第1天销售了78盏,第2天销售了76盏,护眼台灯的销售价格(元/盏)与时向(天)之间符合函数关系式(,且为整数).
(1)日销售量(盏)与时间(天)之间的一次函数关系式为 .
(2)这20天中最大日销售利润是 .
三、解答题
16.用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?
17.为响应政府“节能”号召,某强照明公司减少了白炽灯的生产数量,引进新工艺生产一种新型节能灯,已知这种节能灯的出厂价为每个20元.某商场试销发现,销售单价定为25元/个,每月销售量为250个;每涨价1元,每月少卖10个.
(1)求出每月销售量y(个)与销售单价x(元)之间的函数关系式;
(2)设该商场每月销售这种节能灯获得的利润为w(元)与销售单价x(元)之间的函数关系式;
(3)若每月销售量不少于200个,且每个节能灯的销售利润至少为7元,则销售单价定为多少元时,所获利润最大?最大利润是多少?
18.新冠疫情蔓延全球,口罩成了人们的生活必需品,某药店销售普通口罩和N95口罩,今年8月份的进价如下表:
普通口罩 N95口罩
进价(元/包) 8 20
(1)计划N95口罩每包售价比普通口罩贵16元,7包普通口罩和3包N95口罩总售价相同,求普通口罩和N95口罩每包售价;
(2)①按(1)中售价销售一段时间后发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包,该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天的利润为320元,求此时普通口罩每包售价;
②普通口罩售价为多少元时,利润最大?最大利润为多少元?
19.某游乐场的圆形喷水池中心有一雕塑,从点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为轴,点为原点建立直角坐标系,点在轴上,轴上的点、为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为
.
(1)求雕塑高;
(2)求落水点、之间的距离;
(3)若需要在上的点处竖立一尊高3米的雕塑,且,那么雕塑顶部是否会碰到水柱?请通过计算说明.
参考答案:
1.C
2.C
3.B
4.D
5.B
6.C
7.C
8.D
9.A
10.().
11.1+.
12.
13.
14.20
15. 450
16.当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.
17.(1)
(2)
(3)销售单价定为30元时,所获利润最大,最大利润是2000元.
18.(1)普通口罩和 N95 口罩每包售价分别为12元和28元;(2)①10元;②普通口罩售价为11元时,利润最大,最大利润为500元
19.(1)(2)(3)不会碰到水柱
同课章节目录
