22.1 比例线段 第2课时 成比例线段课件(共20张PPT) 2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 22.1 比例线段 第2课时 成比例线段课件(共20张PPT) 2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 22:12:19 | ||
图片预览






文档简介
(共20张PPT)
22.1 比例线段
第22章
相似形
第 2 课时 成比例线段
●我们每个人手里都有一把自学成才的钥匙:
理想、勤奋、毅力、虚心和科学方法。
——华罗庚
知道线段的比的概念,会计算两条线段的比;(重点)
理解成比例线段的概念;(重点)
掌握成比例线段的判定方法.(难点)
课堂学习总结感悟与知识提升
1
2
3
4
学习目标
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
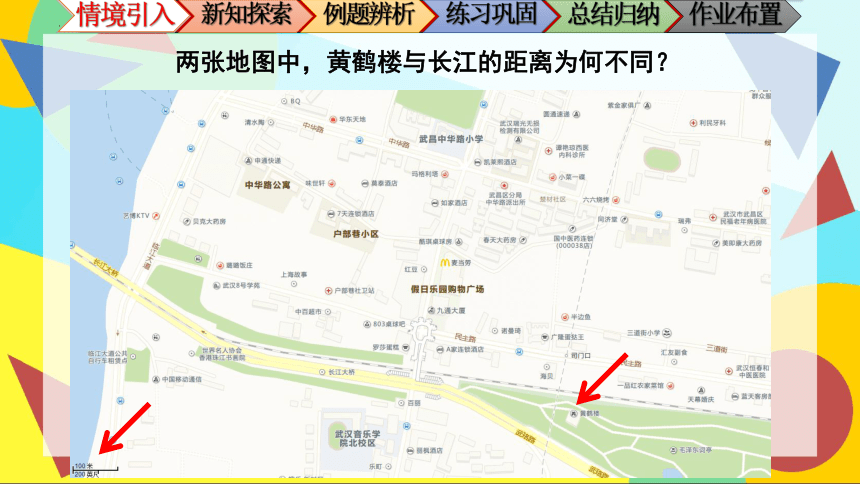
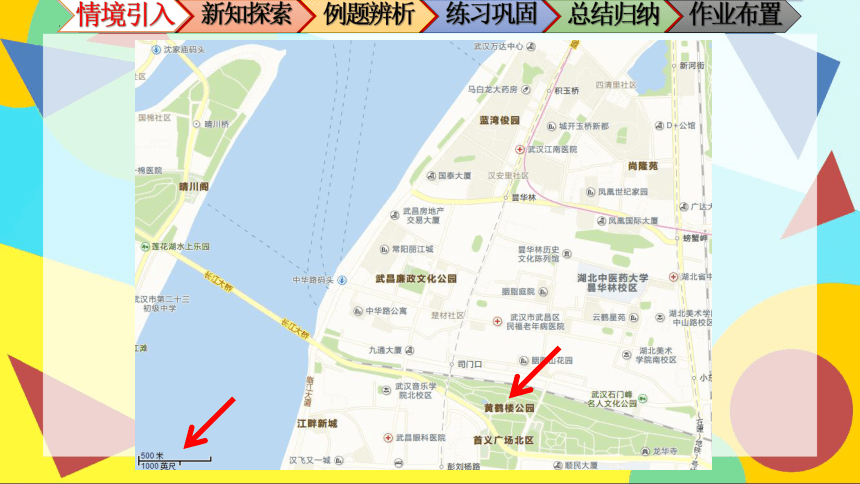
两张地图中,黄鹤楼与长江的距离为何不同?
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
线段的比和成比例线段
已知两条线段a,b,a=2.0 cm,b=1.5 cm,你能求出 吗?
用同一单位长度去度量两条线段a,b,得到它们的长度,我们把这两条线段长度的比叫做这两条线段的比.
记作 或a∶b.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
线段的比和成比例线段
归 纳
由于线段a,b的长度都是正数,所以k是正数;
两条线段的比与所选线段的长度单位无关,但求比时两条线段的长度单位要一致,k没有单位;
除了a=b外, 与 互为倒数.
设
1
2
3
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
线段的比和成比例线段
已知四条线段a,b, c,d, a=2.0 cm,b=3.0 cm,c=4.0 cm,d=6.0 cm,你能说出 与 的关系吗?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
线段的比和成比例线段
归 纳
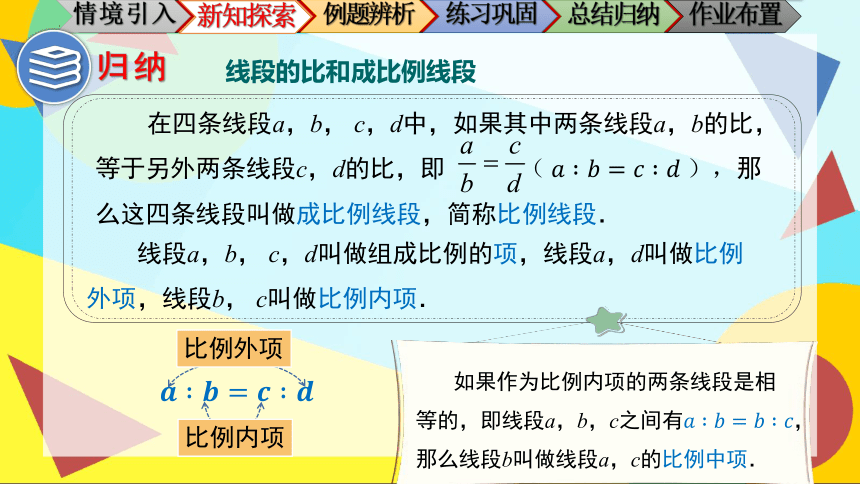
在四条线段a,b, c,d中,如果其中两条线段a,b的比,等于另外两条线段c,d的比,即 ( ),那么这四条线段叫做成比例线段,简称比例线段.
线段a,b, c,d叫做组成比例的项,线段a,d叫做比例外项,线段b, c叫做比例内项.
比例外项
比例内项
如果作为比例内项的两条线段是相等的,即线段a,b,c之间有,那么线段b叫做线段a,c的比例中项.
例:a,b, c,d是成比例线段,是指 ,
而不是 .
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
线段的比和成比例线段
归 纳
四条成比例线段的长度单位要统一;
成比例线段有顺序性.
注意
a,d,c,b是成比例线段.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
判断下列线段a、b、c、d是否是成比例线段:
(1) a=4 cm,b=6 cm,c=5 cm,d=10 cm;
(2) a=10 cm,b=0.2 m,c=30 mm,d=6 cm.
分析
线段a、b、c、d是成比例线段
解: (1) ∵
∴
∴ 线段a、b、c、d 不是成比例线段.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
判断下列线段a、b、c、d是否是成比例线段:
(1) a=4 cm,b=6 cm,c=5 cm,d=10 cm;
(2) a=10 cm,b=0.2 m,c=30 mm,d=6 cm.
注意:求比时线段的长度单位必须统一.
解: (2) ∵ b=0.2 m=20 cm,c=30 mm=3 cm,
∴ ,
∴ 线段a、b、c、d 是成比例线段.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
一块矩形绸布的长AB=am,宽AD=1m,按照图中所示中方式它裁剪成相同的三面矩形彩旗,且使才裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么a的值应当是多少?
D
A
F
E
C
B
解:根据题意可知,AB=am, AE= a m,AD=1m .
由 ,得
即 开平方,得
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 3
在比例尺为1∶1 000 000的地图上,相距3 cm的两地,它们的实际距离为( )
A. 3 km B. 30 km C. 3 00 km D. 3 000 km
知识储备
比例尺=
解:设实际距离为x cm,则3∶x=1∶1 000 000,解得x=3 000 000,3 000 000 cm=30 km.
B
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.一把矩形米尺,长1m,宽3cm,则这把米尺的长和宽的比为( )
A.100:3 B.1:3 C.10:3 D.1000:3
2.甲、乙两地相距35km,图上距离为7cm,则这张图的比例尺为( )
A.5:1 B. 1:5 C.1:500000 D.500000:1
A
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
3.已知三个数2,4,6,添上一个数,使它们能构成一个比
例式,则这个数为 .
,3,12
4.已知线段a=3 cm,b=4 cm,那么线段a,b的比例中项
等于 cm.
2
5.若x:y=1:3,2y=3z,则 的值是( ).
A. B. C. D.
A
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
本节课你有什么收获?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
比例线段
两条线段的比:
比例线段
①长度单位统一;
②与单位无关,本身没有单位;
③两条线段有顺序要求.
①概念:项、比例内项、比例外项;
②四条线段有顺序要求;
③特别地:比例中项.
检查作业: 习题22.1 第2、3、5题
作 业
读书部分:阅读教材相关章节
书面作业:教材习题22.1 (必做)
22.1.2 (选做)
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
作业布置
同学们,再见!
成功无捷径
学习需奋斗
22.1 比例线段
第22章
相似形
第 2 课时 成比例线段
●我们每个人手里都有一把自学成才的钥匙:
理想、勤奋、毅力、虚心和科学方法。
——华罗庚
知道线段的比的概念,会计算两条线段的比;(重点)
理解成比例线段的概念;(重点)
掌握成比例线段的判定方法.(难点)
课堂学习总结感悟与知识提升
1
2
3
4
学习目标
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
两张地图中,黄鹤楼与长江的距离为何不同?
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
线段的比和成比例线段
已知两条线段a,b,a=2.0 cm,b=1.5 cm,你能求出 吗?
用同一单位长度去度量两条线段a,b,得到它们的长度,我们把这两条线段长度的比叫做这两条线段的比.
记作 或a∶b.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
线段的比和成比例线段
归 纳
由于线段a,b的长度都是正数,所以k是正数;
两条线段的比与所选线段的长度单位无关,但求比时两条线段的长度单位要一致,k没有单位;
除了a=b外, 与 互为倒数.
设
1
2
3
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
线段的比和成比例线段
已知四条线段a,b, c,d, a=2.0 cm,b=3.0 cm,c=4.0 cm,d=6.0 cm,你能说出 与 的关系吗?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
线段的比和成比例线段
归 纳
在四条线段a,b, c,d中,如果其中两条线段a,b的比,等于另外两条线段c,d的比,即 ( ),那么这四条线段叫做成比例线段,简称比例线段.
线段a,b, c,d叫做组成比例的项,线段a,d叫做比例外项,线段b, c叫做比例内项.
比例外项
比例内项
如果作为比例内项的两条线段是相等的,即线段a,b,c之间有,那么线段b叫做线段a,c的比例中项.
例:a,b, c,d是成比例线段,是指 ,
而不是 .
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
线段的比和成比例线段
归 纳
四条成比例线段的长度单位要统一;
成比例线段有顺序性.
注意
a,d,c,b是成比例线段.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
判断下列线段a、b、c、d是否是成比例线段:
(1) a=4 cm,b=6 cm,c=5 cm,d=10 cm;
(2) a=10 cm,b=0.2 m,c=30 mm,d=6 cm.
分析
线段a、b、c、d是成比例线段
解: (1) ∵
∴
∴ 线段a、b、c、d 不是成比例线段.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
判断下列线段a、b、c、d是否是成比例线段:
(1) a=4 cm,b=6 cm,c=5 cm,d=10 cm;
(2) a=10 cm,b=0.2 m,c=30 mm,d=6 cm.
注意:求比时线段的长度单位必须统一.
解: (2) ∵ b=0.2 m=20 cm,c=30 mm=3 cm,
∴ ,
∴ 线段a、b、c、d 是成比例线段.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
一块矩形绸布的长AB=am,宽AD=1m,按照图中所示中方式它裁剪成相同的三面矩形彩旗,且使才裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么a的值应当是多少?
D
A
F
E
C
B
解:根据题意可知,AB=am, AE= a m,AD=1m .
由 ,得
即 开平方,得
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 3
在比例尺为1∶1 000 000的地图上,相距3 cm的两地,它们的实际距离为( )
A. 3 km B. 30 km C. 3 00 km D. 3 000 km
知识储备
比例尺=
解:设实际距离为x cm,则3∶x=1∶1 000 000,解得x=3 000 000,3 000 000 cm=30 km.
B
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.一把矩形米尺,长1m,宽3cm,则这把米尺的长和宽的比为( )
A.100:3 B.1:3 C.10:3 D.1000:3
2.甲、乙两地相距35km,图上距离为7cm,则这张图的比例尺为( )
A.5:1 B. 1:5 C.1:500000 D.500000:1
A
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
3.已知三个数2,4,6,添上一个数,使它们能构成一个比
例式,则这个数为 .
,3,12
4.已知线段a=3 cm,b=4 cm,那么线段a,b的比例中项
等于 cm.
2
5.若x:y=1:3,2y=3z,则 的值是( ).
A. B. C. D.
A
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
本节课你有什么收获?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
比例线段
两条线段的比:
比例线段
①长度单位统一;
②与单位无关,本身没有单位;
③两条线段有顺序要求.
①概念:项、比例内项、比例外项;
②四条线段有顺序要求;
③特别地:比例中项.
检查作业: 习题22.1 第2、3、5题
作 业
读书部分:阅读教材相关章节
书面作业:教材习题22.1 (必做)
22.1.2 (选做)
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
作业布置
同学们,再见!
成功无捷径
学习需奋斗
