22.2 相似三角形的判定 第4课时 相似三角形的判定定理3 课件 (共24张PPT) 2023—2024学年沪科版数学九年级上册
文档属性
| 名称 | 22.2 相似三角形的判定 第4课时 相似三角形的判定定理3 课件 (共24张PPT) 2023—2024学年沪科版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 884.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 22:10:56 | ||
图片预览




文档简介
(共24张PPT)
22.2 相似三角形的判定
第22章
相似形
第 4 课时 相似三角形的判定定理3
●我们每个人手里都有一把自学成才的钥匙:
理想、勤奋、毅力、虚心和科学方法。
——华罗庚
理解相似三角形判定定理3的推导过程
掌握相似三角形的判定定理3.(重点)
能熟练运用相似三角形的判定定理3.(难点)
课堂学习总结感悟与知识提升
1
2
3
4
学习目标
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
复习回顾
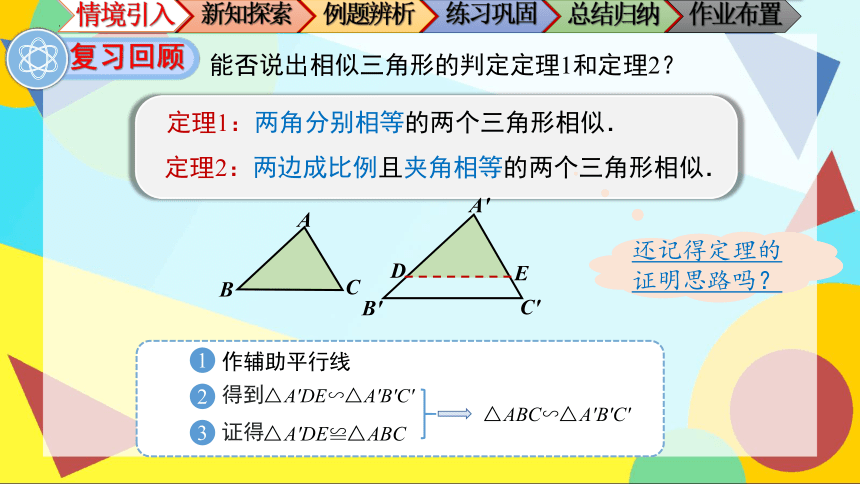
能否说出相似三角形的判定定理1和定理2?
定理1:两角分别相等的两个三角形相似.
还记得定理的证明思路吗?
定理2:两边成比例且夹角相等的两个三角形相似.
A
B
C
A'
B'
C'
D
E
作辅助平行线
得到
证得
1
2
3
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
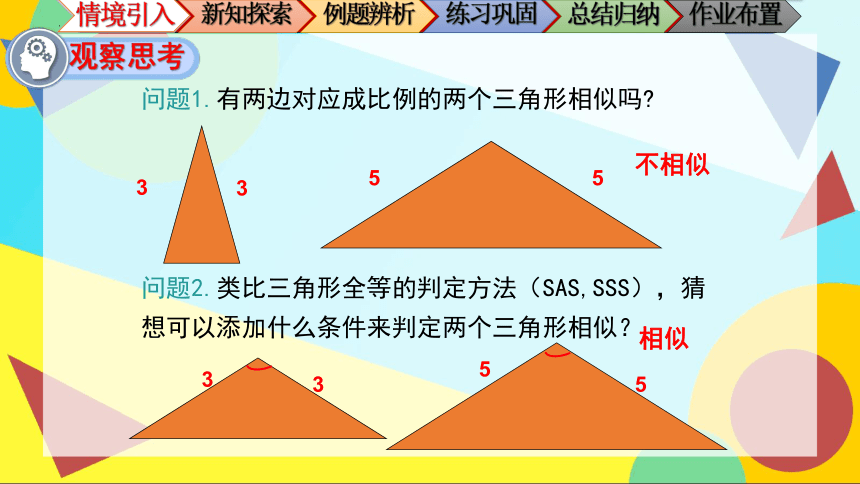
问题1.有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
三边成比例的两个三角形相似
A'
B'
C'
A
B
C
全等三角形
类比
相似三角形
B
C
A
A'
B'
C'
全等三角形是相似三角形的特例.
SSS定理
,
特殊到一般
∴
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
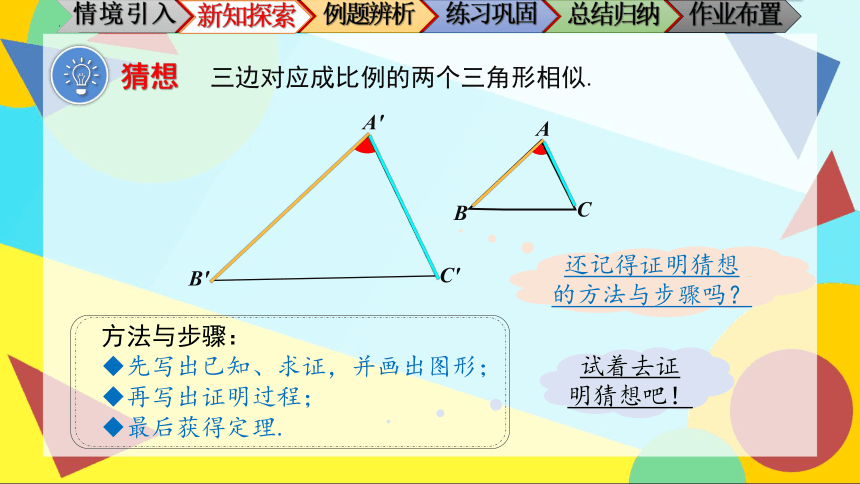
猜想
三边对应成比例的两个三角形相似.
A'
B'
C'
A
B
C
方法与步骤:
先写出已知、求证,并画出图形;
再写出证明过程;
最后获得定理.
还记得证明猜想的方法与步骤吗?
试着去证明猜想吧!
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
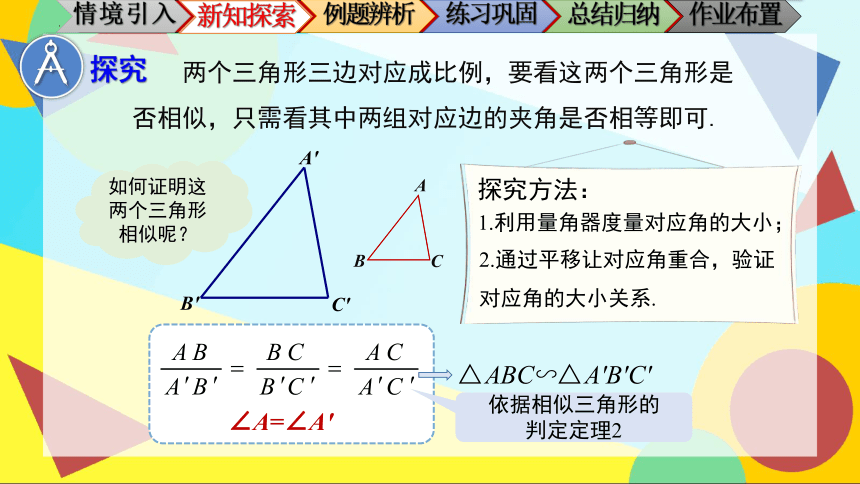
探究
∠A=∠A'
B'
C'
A'
A
B
C
两个三角形三边对应成比例,要看这两个三角形是否相似,只需看其中两组对应边的夹角是否相等即可.
探究方法:
1.利用量角器度量对应角的大小;
2.通过平移让对应角重合,验证对应角的大小关系.
依据相似三角形的
判定定理2
如何证明这两个三角形相似呢?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
证明
分析
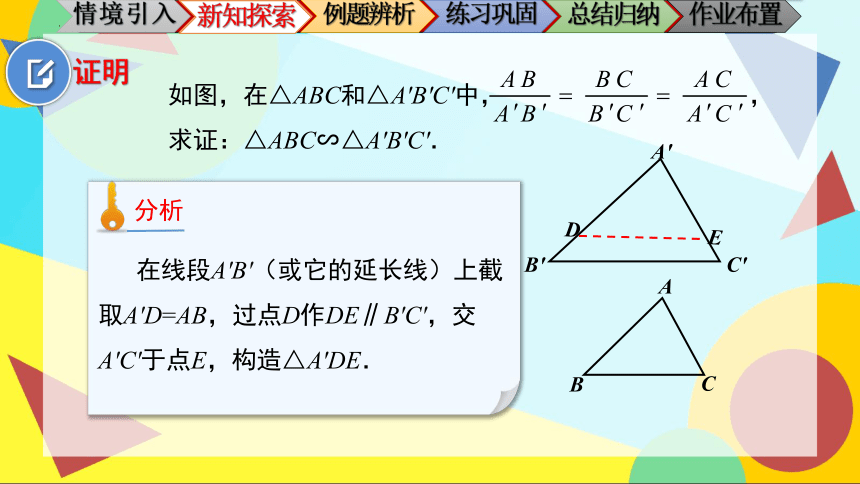
如图,在△ABC和△A'B'C'中, ,
求证:△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,构造△A'DE.
D
E
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
证明
A
B
C
A'
B'
C'
D
E
∴ .
又∵ ,A'D=AB,
∴ , .
∴DE=BC,A'E=AC.
∴△A'DE≌△ABC(SSS).
∴△ABC∽△A'B'C'.
在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,则
△A'DE∽△A'B'C' .
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
归 纳
相似三角形的判定定理3
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
简记为:三边成比例的两个三角形相似.
A
B
C
A'
C'
B'
符号语言 :
在△ABC 和 中,
∴ .
△ABC∽
∵ ,
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
在△ABC和△A'B'C'中,已知下列条件成立,判断这两个三角形是否相似,并说明理由.
(1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°;
(3)AB=2,BC= ,AC= ,A'B' = ,B'C' =1,A' C' = .
解:(1)∵ ,
,
∴ .
∵∠A=∠A' =45°,
∴△ABC∽△A'B'C'.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
在△ABC和△A'B'C'中,已知下列条件成立,判断这两个三角形是否相似,并说明理由.
(1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°;
(3)AB=2,BC= ,AC= ,A'B' = ,B'C' =1,A' C' = .
(2)∵ ∠B=180° (∠A+∠C)
=180° (38°+ 97°)
=45°,
∴ ∠B=∠B'= 45°,
∵∠A=∠A' =38°,
∴△ABC∽△A'B'C'.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
在△ABC和△A'B'C'中,已知下列条件成立,判断这两个三角形是否相似,并说明理由.
(1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°;
(3)AB=2,BC= ,AC= ,A'B' = ,B'C' =1,A' C' = .
(3)∵
∴ .
∴△ABC∽△A'B'C'.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,BC与DE相交于点O.问:
(1)当∠B满足什么条件时,△ABC∽△ADE?
(2)当AC∶AE满足什么条件时,△ABC∽△ADE?
A
B
C
D
E
O
分析
从图中可以看出,在△ABC与△ADE中,∠A=∠A,根据已学的三角形相似的判定定理“AA”,“SAS”,添加相关条件可得△ABC∽△ADE.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,BC与DE相交于点O.问:
(1)当∠B满足什么条件时,△ABC∽△ADE?
(2)当AC∶AE满足什么条件时,△ABC∽△ADE?
A
B
C
D
E
O
解:(1)∵ ∠A=∠A,
∴ 当∠B=∠D时,
△ABC∽△ADE.
(2) ∵ ∠A=∠A,
∴ 当AC∶AE=AB∶AD时,
△ABC∽△ADE.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5 cm,6 cm,另一个三角形框架的一边长为2 cm,怎样选料可使这两个三角形相似?
解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:
(1)如果边长为4,5,6的对应边长分别为2,x,y,
那么:
解得:
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5 cm,6 cm,另一个三角形框架的一边长为2 cm,怎样选料可使这两个三角形相似?
解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:
(2)如果边长为4,5,6的对应边长分别为x,2,y,
那么: ,解得:
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5 cm,6 cm,另一个三角形框架的一边长为2 cm,怎样选料可使这两个三角形相似?
解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:
(3)如果边长为4,5,6的对应边长分别为x,y,2,
那么: ,解得:
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
2. 如图,∠APD=90°,AP=PB=BC=CD,下列结论
正确的是 ( )
A. △PAB∽△PCA B. △PAB∽△PDA
C. △ABC∽△DBA D. △ABC∽△DCA
A
C
B
P
D
C
∵ AB : BC = BD : AB = AD : AC,∴△ABC∽△DBA,故选C.
解析:设AP=PB=BC=CD=1,∵∠APD=90°,∴AB= ,AC= ,AD= .
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
本节课你有什么收获?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
相似三角形的判定定理3
相似三角形的判定定理3:
符号语言:
如果一个三角形的三条边与另一个三角形的三条边对应成比例那么这两个三角形相似.
简记为:三边成比例的两个三角形相似.
在△ABC 和 中,
∴ .
△ABC∽
∵ ,
A
B
C
A'
C'
B'
检查作业: 习题22.2 第2、3、5题
作 业
读书部分:阅读教材相关章节
书面作业:教材习题22.2 (必做)
22.2.2 (选做)
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
作业布置
同学们,再见!
成功无捷径
学习需奋斗
22.2 相似三角形的判定
第22章
相似形
第 4 课时 相似三角形的判定定理3
●我们每个人手里都有一把自学成才的钥匙:
理想、勤奋、毅力、虚心和科学方法。
——华罗庚
理解相似三角形判定定理3的推导过程
掌握相似三角形的判定定理3.(重点)
能熟练运用相似三角形的判定定理3.(难点)
课堂学习总结感悟与知识提升
1
2
3
4
学习目标
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
复习回顾
能否说出相似三角形的判定定理1和定理2?
定理1:两角分别相等的两个三角形相似.
还记得定理的证明思路吗?
定理2:两边成比例且夹角相等的两个三角形相似.
A
B
C
A'
B'
C'
D
E
作辅助平行线
得到
证得
1
2
3
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
问题1.有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
三边成比例的两个三角形相似
A'
B'
C'
A
B
C
全等三角形
类比
相似三角形
B
C
A
A'
B'
C'
全等三角形是相似三角形的特例.
SSS定理
,
特殊到一般
∴
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
猜想
三边对应成比例的两个三角形相似.
A'
B'
C'
A
B
C
方法与步骤:
先写出已知、求证,并画出图形;
再写出证明过程;
最后获得定理.
还记得证明猜想的方法与步骤吗?
试着去证明猜想吧!
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
探究
∠A=∠A'
B'
C'
A'
A
B
C
两个三角形三边对应成比例,要看这两个三角形是否相似,只需看其中两组对应边的夹角是否相等即可.
探究方法:
1.利用量角器度量对应角的大小;
2.通过平移让对应角重合,验证对应角的大小关系.
依据相似三角形的
判定定理2
如何证明这两个三角形相似呢?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
证明
分析
如图,在△ABC和△A'B'C'中, ,
求证:△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,构造△A'DE.
D
E
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
证明
A
B
C
A'
B'
C'
D
E
∴ .
又∵ ,A'D=AB,
∴ , .
∴DE=BC,A'E=AC.
∴△A'DE≌△ABC(SSS).
∴△ABC∽△A'B'C'.
在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,则
△A'DE∽△A'B'C' .
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
归 纳
相似三角形的判定定理3
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
简记为:三边成比例的两个三角形相似.
A
B
C
A'
C'
B'
符号语言 :
在△ABC 和 中,
∴ .
△ABC∽
∵ ,
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
在△ABC和△A'B'C'中,已知下列条件成立,判断这两个三角形是否相似,并说明理由.
(1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°;
(3)AB=2,BC= ,AC= ,A'B' = ,B'C' =1,A' C' = .
解:(1)∵ ,
,
∴ .
∵∠A=∠A' =45°,
∴△ABC∽△A'B'C'.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
在△ABC和△A'B'C'中,已知下列条件成立,判断这两个三角形是否相似,并说明理由.
(1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°;
(3)AB=2,BC= ,AC= ,A'B' = ,B'C' =1,A' C' = .
(2)∵ ∠B=180° (∠A+∠C)
=180° (38°+ 97°)
=45°,
∴ ∠B=∠B'= 45°,
∵∠A=∠A' =38°,
∴△ABC∽△A'B'C'.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
在△ABC和△A'B'C'中,已知下列条件成立,判断这两个三角形是否相似,并说明理由.
(1)AB=5,AC=3,∠A=45°,A'B' =10,A'C' =6,∠A' =45°;
(2)∠A=38°,∠C=97°,∠A'=38°,∠B'=45°;
(3)AB=2,BC= ,AC= ,A'B' = ,B'C' =1,A' C' = .
(3)∵
∴ .
∴△ABC∽△A'B'C'.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,BC与DE相交于点O.问:
(1)当∠B满足什么条件时,△ABC∽△ADE?
(2)当AC∶AE满足什么条件时,△ABC∽△ADE?
A
B
C
D
E
O
分析
从图中可以看出,在△ABC与△ADE中,∠A=∠A,根据已学的三角形相似的判定定理“AA”,“SAS”,添加相关条件可得△ABC∽△ADE.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,BC与DE相交于点O.问:
(1)当∠B满足什么条件时,△ABC∽△ADE?
(2)当AC∶AE满足什么条件时,△ABC∽△ADE?
A
B
C
D
E
O
解:(1)∵ ∠A=∠A,
∴ 当∠B=∠D时,
△ABC∽△ADE.
(2) ∵ ∠A=∠A,
∴ 当AC∶AE=AB∶AD时,
△ABC∽△ADE.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5 cm,6 cm,另一个三角形框架的一边长为2 cm,怎样选料可使这两个三角形相似?
解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:
(1)如果边长为4,5,6的对应边长分别为2,x,y,
那么:
解得:
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5 cm,6 cm,另一个三角形框架的一边长为2 cm,怎样选料可使这两个三角形相似?
解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:
(2)如果边长为4,5,6的对应边长分别为x,2,y,
那么: ,解得:
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.要做两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4 cm,5 cm,6 cm,另一个三角形框架的一边长为2 cm,怎样选料可使这两个三角形相似?
解:要使这两个三角形相似,则这两个三角形的三边对应成比例.有三种情况:
(3)如果边长为4,5,6的对应边长分别为x,y,2,
那么: ,解得:
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
2. 如图,∠APD=90°,AP=PB=BC=CD,下列结论
正确的是 ( )
A. △PAB∽△PCA B. △PAB∽△PDA
C. △ABC∽△DBA D. △ABC∽△DCA
A
C
B
P
D
C
∵ AB : BC = BD : AB = AD : AC,∴△ABC∽△DBA,故选C.
解析:设AP=PB=BC=CD=1,∵∠APD=90°,∴AB= ,AC= ,AD= .
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
本节课你有什么收获?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
相似三角形的判定定理3
相似三角形的判定定理3:
符号语言:
如果一个三角形的三条边与另一个三角形的三条边对应成比例那么这两个三角形相似.
简记为:三边成比例的两个三角形相似.
在△ABC 和 中,
∴ .
△ABC∽
∵ ,
A
B
C
A'
C'
B'
检查作业: 习题22.2 第2、3、5题
作 业
读书部分:阅读教材相关章节
书面作业:教材习题22.2 (必做)
22.2.2 (选做)
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
作业布置
同学们,再见!
成功无捷径
学习需奋斗
