三垂线定理
图片预览






文档简介
课件24张PPT。三垂线定理这是偶然的巧合,还是必然?cos?·cos?=cos?A?aOPPO⊥ a?
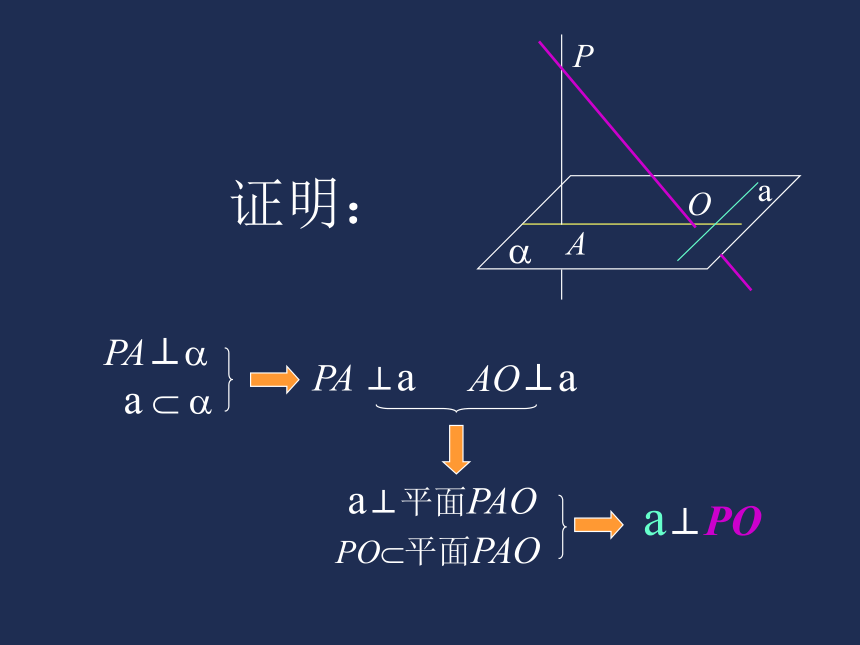
已知 PA、PO分别是平面?的垂线、斜线,AO是PO在平面?上的射影。a? ?,a⊥AO。
求证: a⊥PO在平面内的一条直线,如果和这个平面的一条
斜线的射影垂直,那么,它就和这条斜线垂直。三垂线定理证明:a⊥POPA⊥?
a ? ?AO⊥aa⊥平面PAOPO?平面PAOPA ⊥a三垂线定理: 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。例1 已知P 是平面ABC 外一点, PA⊥平面ABC ,AC ⊥ BC, 求证: PC ⊥ BC证明:∵ P 是平面ABC 外一点
PA⊥平面ABC
∴PC是平面ABC的斜线
∴AC是PC在平面ABC上的射影
∵BC?平面ABC 且AC ⊥ BC
∴由三垂线定理得
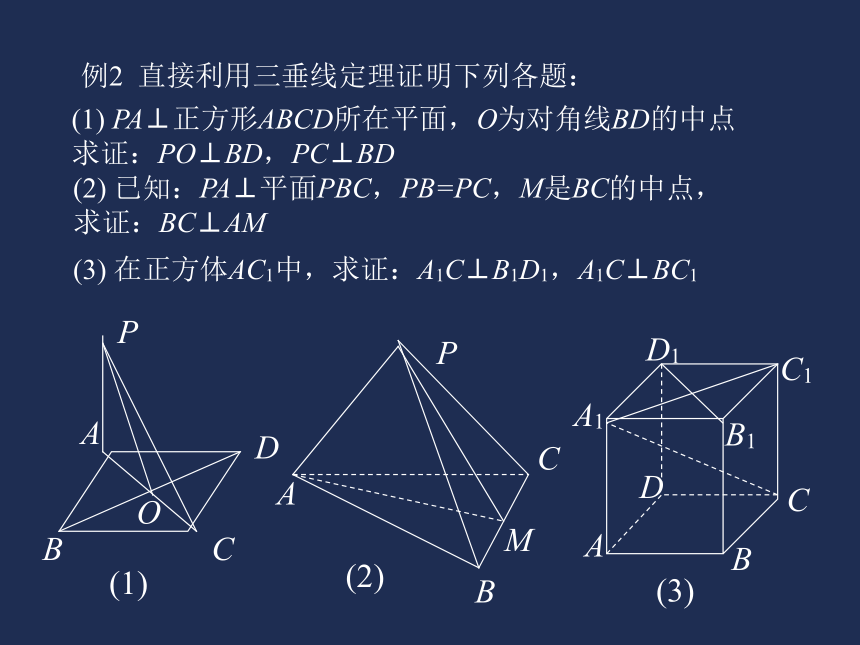
PC ⊥ BC例2 直接利用三垂线定理证明下列各题:(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点
求证:PO⊥BD,PC⊥BD(3) 在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1(2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点,
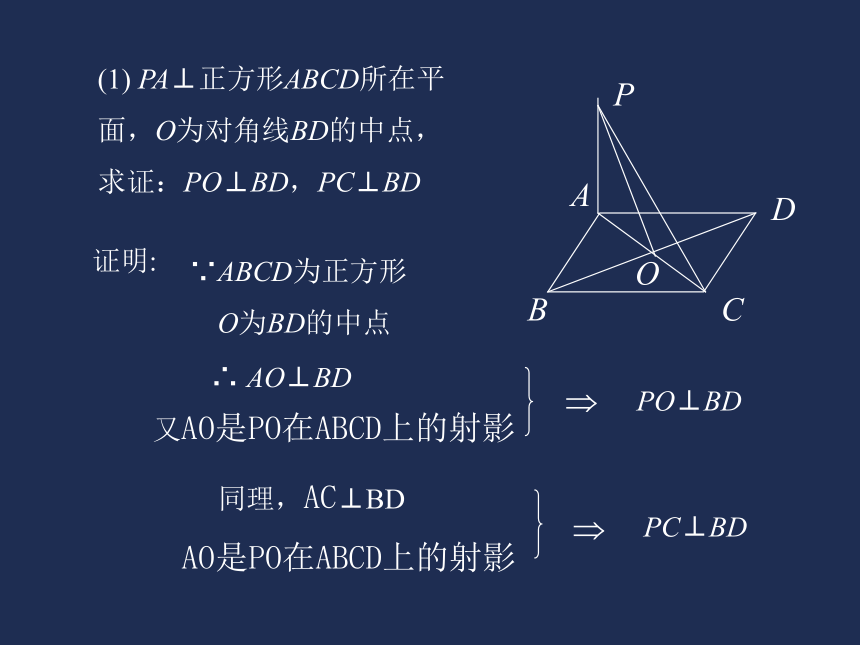
求证:BC⊥AM(1)(2)(3)(1) PA⊥正方形ABCD所在平
面,O为对角线BD的中点,
求证:PO⊥BD,PC⊥BD证明:∵ABCD为正方形
O为BD的中点∴ AO⊥BD又AO是PO在ABCD上的射影??PO⊥BD(2) 已知:PA⊥平面PBC,PB=PC,
M是BC的中点,
求证:BC⊥AMBC⊥AM证明:∵ PB=PC
M是BC的中点??PM ⊥BC∵PA⊥平面PBC∴PM是AM在平面PBC上的射影??(3) 在正方体AC1中,
求证:A1C⊥BC1 , A1C⊥B1D1 ∵在正方体AC1中
A1B1⊥面BCC1B1且BC1 ⊥B1C
∴B1C是A1C在面BCC1B1上的射影证明:同理可证, A1C⊥B1D1由三垂线定理知
A1C⊥BC1 我们要学会从纷繁的已知条件中找出
或者创造出符合三垂线定理的条件解题回顾,怎么找?三垂线定理解题的关键:找三垂!怎么找?一找直线和平面垂直二找平面的斜线在平面
内的射影和平面内的
一条直线垂直注意:由一垂、二垂直接得出第三垂
并不是三垂都作为已知条件解题回顾三垂线定理是平面的一条斜线与平面内的直线垂直的判定定理,这两条直线可以是: ①相交直线 ②异面直线使用三垂线定理还应注意些什么?解题回顾直线a 在一定要在平面内,如果 a 不在平面内,定理就不一定成立。例如:当 b⊥? 时,
b⊥OA注意:如果将定理中
“在平面内”的条件
去掉,结论仍然成立
吗?但 b不垂直于OP 解题回顾√×面ABCD →面α
直线A1C →斜线 a
直线B1B →垂线 b××面ABCD →面α
面B1BCC1→面β
直线A1C →斜线 a
直线AB →垂线 b面ABCD →面α
直线A1C →斜线 a
直线B1B →垂线 b已知:PA,PO分别是平
面? 的垂线和斜线,AO
是PO在平面? 的射影,
a ? ? , a ⊥AO,
l 平行于 a 。
求证: l 垂直于PO⑷若a是平面α的斜线,b∥α,直线 b垂直
于a在平面α内的射影,则 a⊥b三垂线定理包含几种垂直关系?②线射垂直①线面垂直③ 线斜垂直直 线 和
平面垂直平面内的直线和平面一条斜线的射影垂直平面内的直线和平面的一条斜线垂直线射垂直线斜垂直平面内的一条直线和平面的一条斜线在平面内的射影垂直平面内的一条直线和平面的一条斜线垂直
三垂线定理的逆定理? 在平面内的一条直线,如果和这个平面的一
条斜线垂直,那么,它也和这条斜线的射影垂直。
已知:PA,PO分
别是平面? 的垂线和斜
线,AO是PO在平面?
的射影,a ? ? ,a ⊥PO
求证:a ⊥AO三垂线定理的逆定理三垂线定理的逆定理 在平面内的一条直线,如果和这个平面的一条斜线垂直,那么,它也和这条斜线的射影垂直。三垂线定理: 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。定
理逆
定
理例3 如果一个角所在平面外一点到角的两边距离相等,
那么这一点在平面上的射影在这个角的平分线上。已知:∠BAC在平面?内,点P??,PE⊥AB,PF⊥AC,
PO⊥? ,垂足分别是E、F、O,PE=PF
求证:∠BAO=∠CAO分析: 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥ACP ???证明:∵ PO ⊥? ∴OE、OF是PE、PF在?内的射影∵ PE=PF∴ OE=OF由OE是PE的射影且PE⊥AB??OE⊥AB同理可得OF⊥AC结论成立例4 在四面体ABCD中,已知AB⊥CD,AC⊥BD
求证:AD⊥BC∴DO⊥BC,于是AD⊥BC.证明:作AO⊥平面BCD于点O,
连接BO,CO,DO,则BO,
CO,DO分别为AB,AC,
AD在平面BCD上的射影。O∵AB⊥CD,∴BO⊥CD,同理CO⊥BD,于是O是△BCD的垂心,1. 在正方体AC1中,E、G分别是AA1和
CC1的中点, F在AB上,且C1E⊥EF,
则EF与GD所成的角的大小为( )
(A) 30° (B) 45° (C) 60°(D) 90°DM EB1是EC1在平面AB1
内的射影EB1 ⊥EF
DG∥AM∥EB1
EF ⊥DG练习与作业2.已知 PA、PB、PC两两垂直,
求证:P在平面ABC内的射影是
△ABC的垂心。3.经过一个角的顶点引这个角
所在平面的斜线,如果斜线和
这个角两边的夹角相等,那么
斜线在平面上的射影是这个角
的平分线所在的直线。4.在ABCD—A1B1C1D1中,
求证:AC1⊥平面BC1D
已知 PA、PO分别是平面?的垂线、斜线,AO是PO在平面?上的射影。a? ?,a⊥AO。
求证: a⊥PO在平面内的一条直线,如果和这个平面的一条
斜线的射影垂直,那么,它就和这条斜线垂直。三垂线定理证明:a⊥POPA⊥?
a ? ?AO⊥aa⊥平面PAOPO?平面PAOPA ⊥a三垂线定理: 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。例1 已知P 是平面ABC 外一点, PA⊥平面ABC ,AC ⊥ BC, 求证: PC ⊥ BC证明:∵ P 是平面ABC 外一点
PA⊥平面ABC
∴PC是平面ABC的斜线
∴AC是PC在平面ABC上的射影
∵BC?平面ABC 且AC ⊥ BC
∴由三垂线定理得
PC ⊥ BC例2 直接利用三垂线定理证明下列各题:(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点
求证:PO⊥BD,PC⊥BD(3) 在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1(2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点,
求证:BC⊥AM(1)(2)(3)(1) PA⊥正方形ABCD所在平
面,O为对角线BD的中点,
求证:PO⊥BD,PC⊥BD证明:∵ABCD为正方形
O为BD的中点∴ AO⊥BD又AO是PO在ABCD上的射影??PO⊥BD(2) 已知:PA⊥平面PBC,PB=PC,
M是BC的中点,
求证:BC⊥AMBC⊥AM证明:∵ PB=PC
M是BC的中点??PM ⊥BC∵PA⊥平面PBC∴PM是AM在平面PBC上的射影??(3) 在正方体AC1中,
求证:A1C⊥BC1 , A1C⊥B1D1 ∵在正方体AC1中
A1B1⊥面BCC1B1且BC1 ⊥B1C
∴B1C是A1C在面BCC1B1上的射影证明:同理可证, A1C⊥B1D1由三垂线定理知
A1C⊥BC1 我们要学会从纷繁的已知条件中找出
或者创造出符合三垂线定理的条件解题回顾,怎么找?三垂线定理解题的关键:找三垂!怎么找?一找直线和平面垂直二找平面的斜线在平面
内的射影和平面内的
一条直线垂直注意:由一垂、二垂直接得出第三垂
并不是三垂都作为已知条件解题回顾三垂线定理是平面的一条斜线与平面内的直线垂直的判定定理,这两条直线可以是: ①相交直线 ②异面直线使用三垂线定理还应注意些什么?解题回顾直线a 在一定要在平面内,如果 a 不在平面内,定理就不一定成立。例如:当 b⊥? 时,
b⊥OA注意:如果将定理中
“在平面内”的条件
去掉,结论仍然成立
吗?但 b不垂直于OP 解题回顾√×面ABCD →面α
直线A1C →斜线 a
直线B1B →垂线 b××面ABCD →面α
面B1BCC1→面β
直线A1C →斜线 a
直线AB →垂线 b面ABCD →面α
直线A1C →斜线 a
直线B1B →垂线 b已知:PA,PO分别是平
面? 的垂线和斜线,AO
是PO在平面? 的射影,
a ? ? , a ⊥AO,
l 平行于 a 。
求证: l 垂直于PO⑷若a是平面α的斜线,b∥α,直线 b垂直
于a在平面α内的射影,则 a⊥b三垂线定理包含几种垂直关系?②线射垂直①线面垂直③ 线斜垂直直 线 和
平面垂直平面内的直线和平面一条斜线的射影垂直平面内的直线和平面的一条斜线垂直线射垂直线斜垂直平面内的一条直线和平面的一条斜线在平面内的射影垂直平面内的一条直线和平面的一条斜线垂直
三垂线定理的逆定理? 在平面内的一条直线,如果和这个平面的一
条斜线垂直,那么,它也和这条斜线的射影垂直。
已知:PA,PO分
别是平面? 的垂线和斜
线,AO是PO在平面?
的射影,a ? ? ,a ⊥PO
求证:a ⊥AO三垂线定理的逆定理三垂线定理的逆定理 在平面内的一条直线,如果和这个平面的一条斜线垂直,那么,它也和这条斜线的射影垂直。三垂线定理: 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。定
理逆
定
理例3 如果一个角所在平面外一点到角的两边距离相等,
那么这一点在平面上的射影在这个角的平分线上。已知:∠BAC在平面?内,点P??,PE⊥AB,PF⊥AC,
PO⊥? ,垂足分别是E、F、O,PE=PF
求证:∠BAO=∠CAO分析: 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥ACP ???证明:∵ PO ⊥? ∴OE、OF是PE、PF在?内的射影∵ PE=PF∴ OE=OF由OE是PE的射影且PE⊥AB??OE⊥AB同理可得OF⊥AC结论成立例4 在四面体ABCD中,已知AB⊥CD,AC⊥BD
求证:AD⊥BC∴DO⊥BC,于是AD⊥BC.证明:作AO⊥平面BCD于点O,
连接BO,CO,DO,则BO,
CO,DO分别为AB,AC,
AD在平面BCD上的射影。O∵AB⊥CD,∴BO⊥CD,同理CO⊥BD,于是O是△BCD的垂心,1. 在正方体AC1中,E、G分别是AA1和
CC1的中点, F在AB上,且C1E⊥EF,
则EF与GD所成的角的大小为( )
(A) 30° (B) 45° (C) 60°(D) 90°DM EB1是EC1在平面AB1
内的射影EB1 ⊥EF
DG∥AM∥EB1
EF ⊥DG练习与作业2.已知 PA、PB、PC两两垂直,
求证:P在平面ABC内的射影是
△ABC的垂心。3.经过一个角的顶点引这个角
所在平面的斜线,如果斜线和
这个角两边的夹角相等,那么
斜线在平面上的射影是这个角
的平分线所在的直线。4.在ABCD—A1B1C1D1中,
求证:AC1⊥平面BC1D
