2.2轴对称的性质随堂练习-苏科版数学八年级上册(含答案)
文档属性
| 名称 | 2.2轴对称的性质随堂练习-苏科版数学八年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 470.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 20:22:40 | ||
图片预览

文档简介
2.2轴对称的性质随堂练习-苏科版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.把的每一个点横坐标都乘,得到,这一变换是( )
A.位似变换 B.旋转变换
C.中心对称变换 D.轴对称变换
2.把一张长方形纸片沿折叠后与的交点为,、分别在的位置上,若,则( )
A. B. C. D.
3.若点P的坐标为(3,4 ),则点P关于x轴对称点的点P′的坐标为( )
A.(4,-3 ) B.(3,-4 ) C.(-4,3 ) D.(-3,4)
4.如图,中,,沿折叠,使点B恰好落在边上的点E处.若,则等于( )
A.69° B.67° C.66° D.42°
5.下列命题中,不正确的是( )
A.关于某条直线对称的两个三角形全等
B.若两个图形关于直线对称,则对称轴是对应点连线的垂直平分线
C.等腰三角形一边上的高、中线及这边所对角的平分线重合
D.两个全等的三角形不一定是轴对称图形
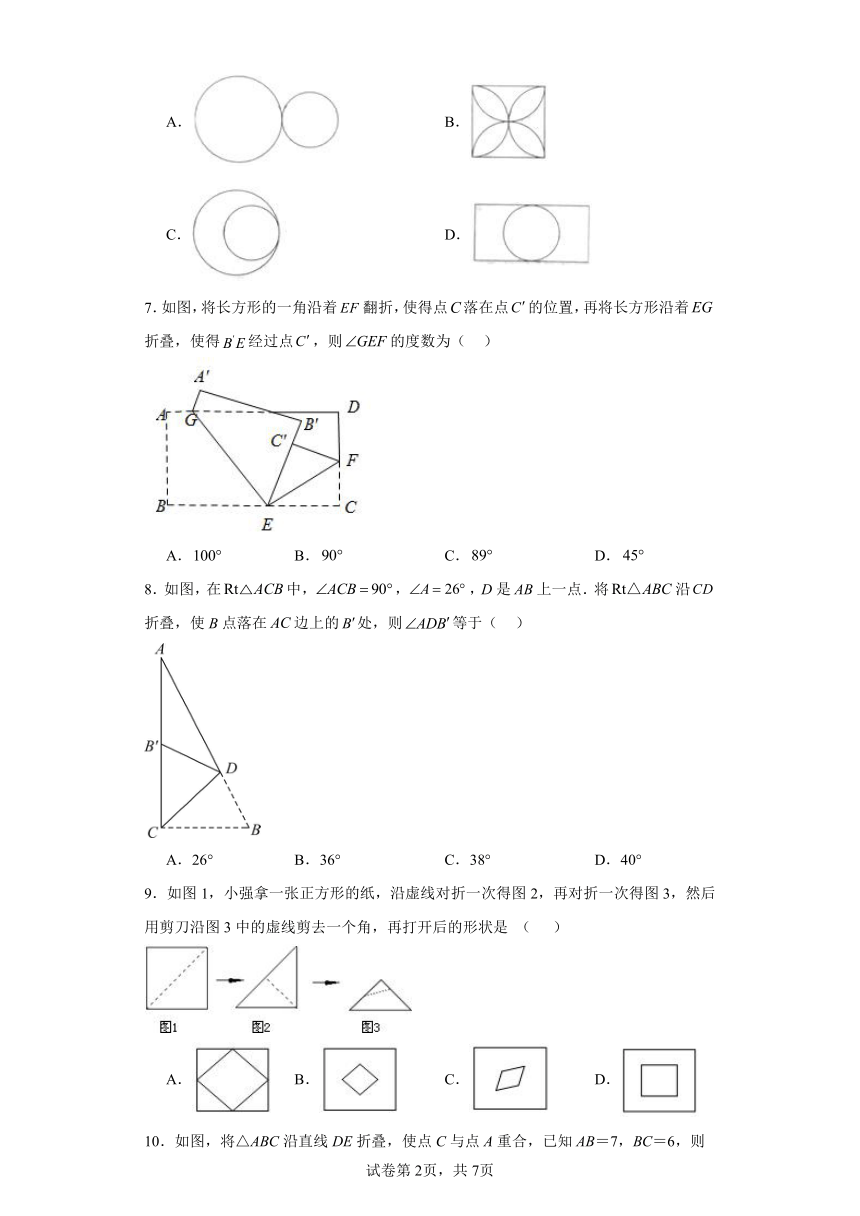
6.下面的图形中对称轴最多的是( )
A. B.
C. D.
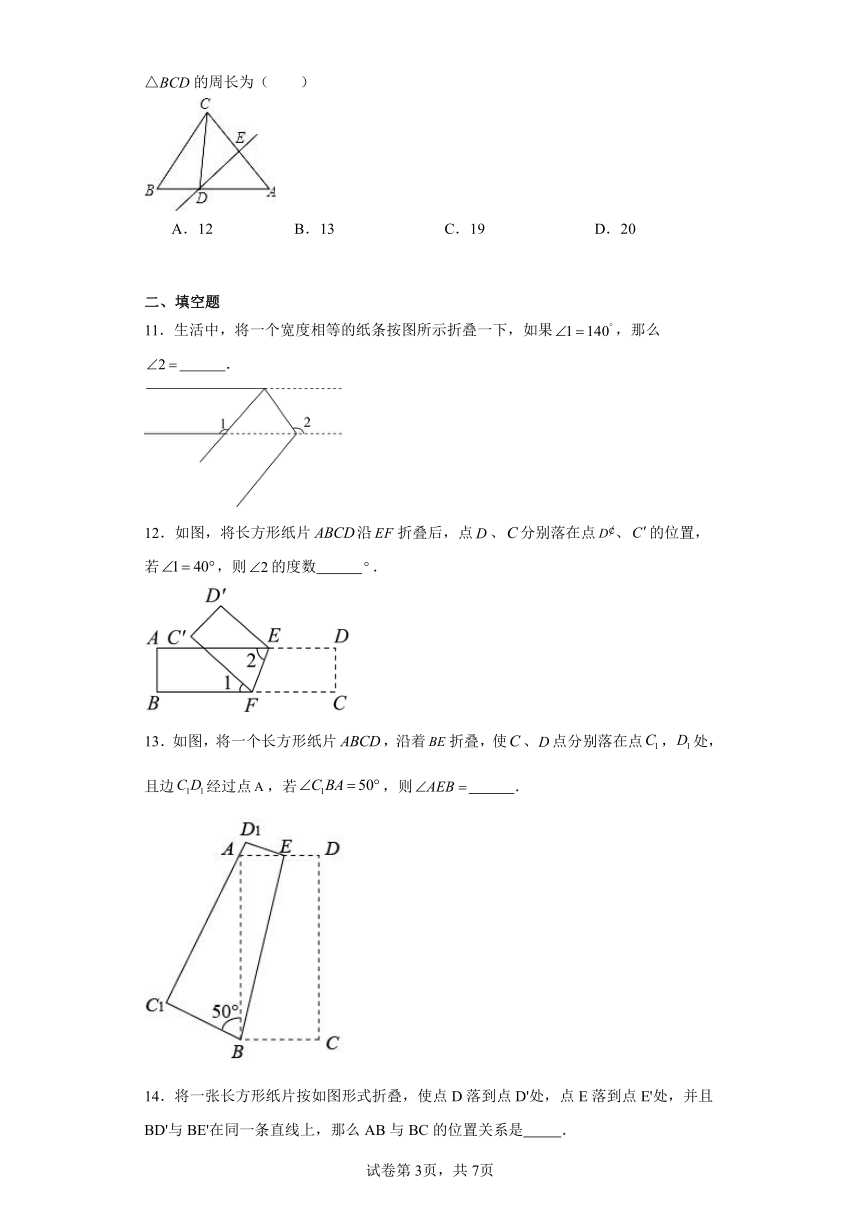
7.如图,将长方形的一角沿着翻折,使得点落在点的位置,再将长方形沿着折叠,使得经过点,则的度数为( )
A. B. C. D.
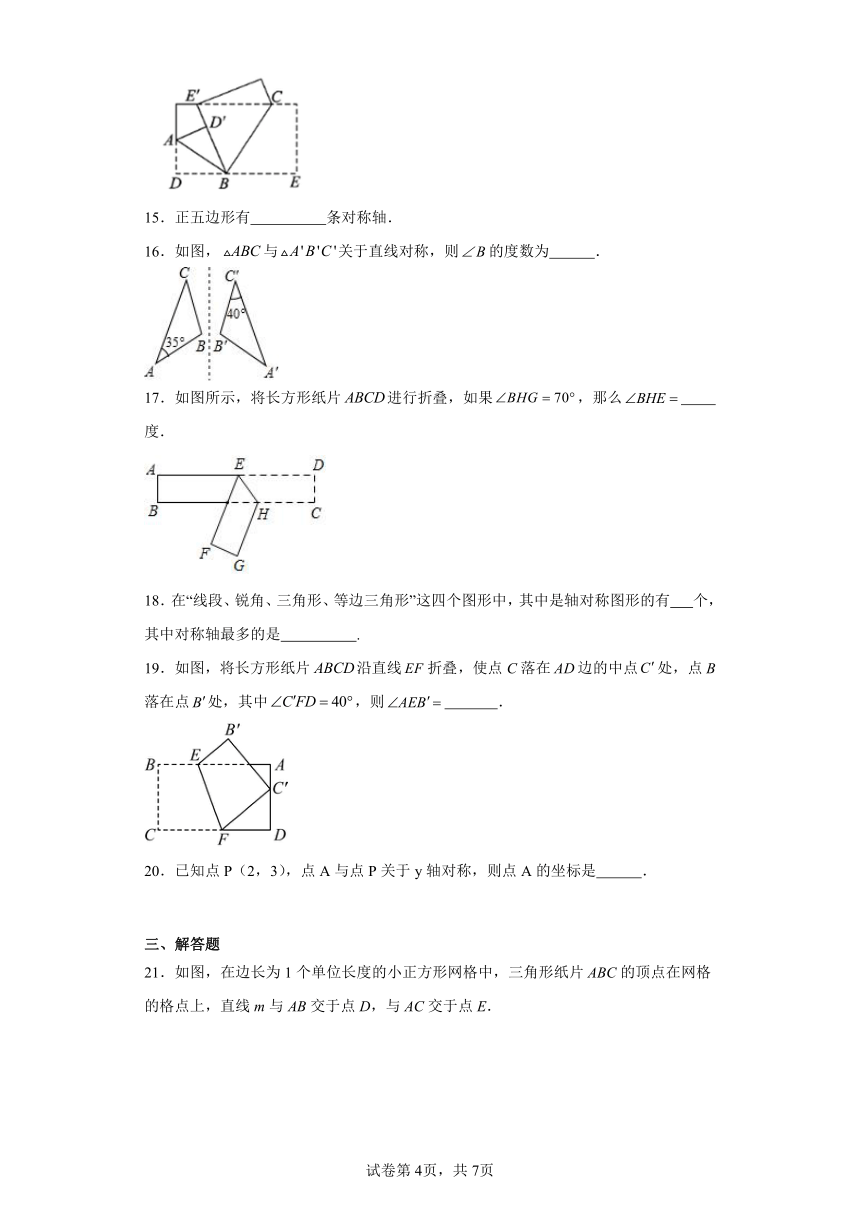
8.如图,在中,,,D是上一点.将沿折叠,使B点落在边上的处,则等于( )
A.26° B.36° C.38° D.40°
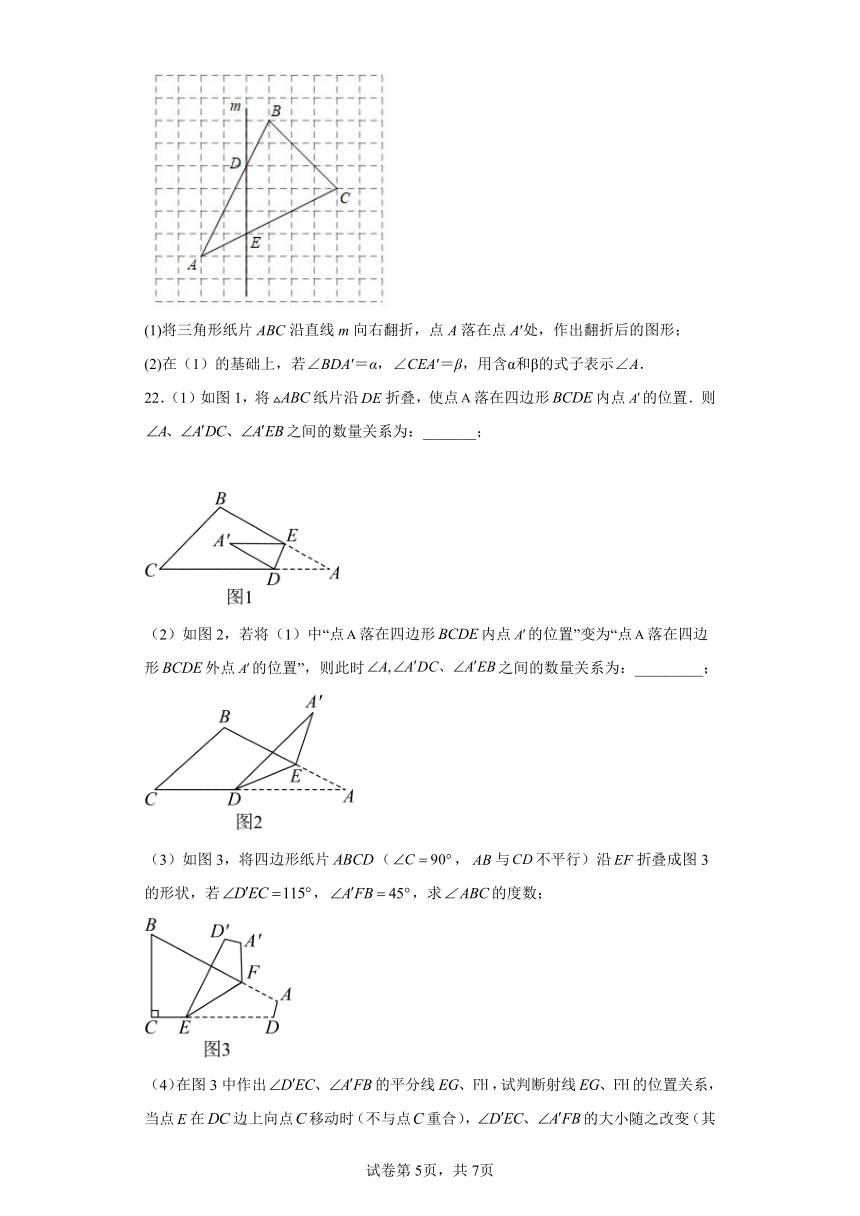
9.如图1,小强拿一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线剪去一个角,再打开后的形状是 ( )
A. B. C. D.
10.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12 B.13 C.19 D.20
二、填空题
11.生活中,将一个宽度相等的纸条按图所示折叠一下,如果,那么 .
12.如图,将长方形纸片沿折叠后,点、分别落在点、的位置,若,则的度数 .
13.如图,将一个长方形纸片,沿着折叠,使、点分别落在点,处,且边经过点,若,则 .
14.将一张长方形纸片按如图形式折叠,使点D落到点D'处,点E落到点E'处,并且BD'与BE'在同一条直线上,那么AB与BC的位置关系是 .
15.正五边形有 条对称轴.
16.如图,与关于直线对称,则的度数为 .
17.如图所示,将长方形纸片进行折叠,如果,那么 度.
18.在“线段、锐角、三角形、等边三角形”这四个图形中,其中是轴对称图形的有 个,其中对称轴最多的是 .
19.如图,将长方形纸片沿直线折叠,使点C落在边的中点处,点B落在点处,其中,则 .
20.已知点P(2,3),点A与点P关于y轴对称,则点A的坐标是 .
三、解答题
21.如图,在边长为1个单位长度的小正方形网格中,三角形纸片ABC的顶点在网格的格点上,直线m与AB交于点D,与AC交于点E.
(1)将三角形纸片ABC沿直线m向右翻折,点A落在点A′处,作出翻折后的图形;
(2)在(1)的基础上,若∠BDA′=α,∠CEA′=β,用含α和β的式子表示∠A.
22.(1)如图1,将纸片沿折叠,使点落在四边形内点的位置.则之间的数量关系为:_______;
(2)如图2,若将(1)中“点落在四边形内点的位置”变为“点落在四边形外点的位置”,则此时之间的数量关系为:_________;
(3)如图3,将四边形纸片(,与不平行)沿折叠成图3的形状,若,,求的度数;
(4)在图3中作出的平分线,试判断射线的位置关系,当点在边上向点移动时(不与点重合),的大小随之改变(其它条件不变),上述,的位置关系改变吗?为什么?
23.如图,四边形与四边形关于直线对称.
(1)点,,,的对称点分别是______,线段,的对称线段分别是______,______,______,______.
(2)与平行吗?为什么?
(3)若与平行,则能说明轴对称图形中对称点的连线一定互相平行吗?
24.如图,在平面直角坐标系中,A(﹣1,3)、B(﹣5,1)、C(﹣2,1).
(1)△ABC的面积为______.
(2)在图中作出△ABC关于x轴的对称图形△A1B1C1,并写出点A1的坐标.
(3)请说明△A2B2C2是由△A1B1C1经过怎样的变换得到的?
25.如图所示.
(1)作出关于轴对称的图形;
(2)在轴上确定一点,使得最小;
(3)求出的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.B
3.B
4.A
5.C
6.B
7.B
8.C
9.C
10.B
11.110°
12.70
13.70°/70度
14.AB⊥BC
15.五
16.105°
17.55
18. 3 等边三角形
19./40度
20.(-2,3)
21.(1)略
(2)
22.(1),(2);(3);(4)位置不改变,.
23.(1)E,F,G,H;EF,EH;GH;∠GFE;∠EHG;(2)AE∥BF;(3)AE与BF平行,不一定能说明轴对称图形对称点的连线互相平行,也有可能共线.
24.(1)3;(2)点A1的坐标为(﹣1,﹣3);(3)△A2B2C2是由△A1B1C1经过关于y轴对称得到.
25.(1)如图所示;(2)如图所示点P;(3);
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.把的每一个点横坐标都乘,得到,这一变换是( )
A.位似变换 B.旋转变换
C.中心对称变换 D.轴对称变换
2.把一张长方形纸片沿折叠后与的交点为,、分别在的位置上,若,则( )
A. B. C. D.
3.若点P的坐标为(3,4 ),则点P关于x轴对称点的点P′的坐标为( )
A.(4,-3 ) B.(3,-4 ) C.(-4,3 ) D.(-3,4)
4.如图,中,,沿折叠,使点B恰好落在边上的点E处.若,则等于( )
A.69° B.67° C.66° D.42°
5.下列命题中,不正确的是( )
A.关于某条直线对称的两个三角形全等
B.若两个图形关于直线对称,则对称轴是对应点连线的垂直平分线
C.等腰三角形一边上的高、中线及这边所对角的平分线重合
D.两个全等的三角形不一定是轴对称图形
6.下面的图形中对称轴最多的是( )
A. B.
C. D.
7.如图,将长方形的一角沿着翻折,使得点落在点的位置,再将长方形沿着折叠,使得经过点,则的度数为( )
A. B. C. D.
8.如图,在中,,,D是上一点.将沿折叠,使B点落在边上的处,则等于( )
A.26° B.36° C.38° D.40°
9.如图1,小强拿一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线剪去一个角,再打开后的形状是 ( )
A. B. C. D.
10.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12 B.13 C.19 D.20
二、填空题
11.生活中,将一个宽度相等的纸条按图所示折叠一下,如果,那么 .
12.如图,将长方形纸片沿折叠后,点、分别落在点、的位置,若,则的度数 .
13.如图,将一个长方形纸片,沿着折叠,使、点分别落在点,处,且边经过点,若,则 .
14.将一张长方形纸片按如图形式折叠,使点D落到点D'处,点E落到点E'处,并且BD'与BE'在同一条直线上,那么AB与BC的位置关系是 .
15.正五边形有 条对称轴.
16.如图,与关于直线对称,则的度数为 .
17.如图所示,将长方形纸片进行折叠,如果,那么 度.
18.在“线段、锐角、三角形、等边三角形”这四个图形中,其中是轴对称图形的有 个,其中对称轴最多的是 .
19.如图,将长方形纸片沿直线折叠,使点C落在边的中点处,点B落在点处,其中,则 .
20.已知点P(2,3),点A与点P关于y轴对称,则点A的坐标是 .
三、解答题
21.如图,在边长为1个单位长度的小正方形网格中,三角形纸片ABC的顶点在网格的格点上,直线m与AB交于点D,与AC交于点E.
(1)将三角形纸片ABC沿直线m向右翻折,点A落在点A′处,作出翻折后的图形;
(2)在(1)的基础上,若∠BDA′=α,∠CEA′=β,用含α和β的式子表示∠A.
22.(1)如图1,将纸片沿折叠,使点落在四边形内点的位置.则之间的数量关系为:_______;
(2)如图2,若将(1)中“点落在四边形内点的位置”变为“点落在四边形外点的位置”,则此时之间的数量关系为:_________;
(3)如图3,将四边形纸片(,与不平行)沿折叠成图3的形状,若,,求的度数;
(4)在图3中作出的平分线,试判断射线的位置关系,当点在边上向点移动时(不与点重合),的大小随之改变(其它条件不变),上述,的位置关系改变吗?为什么?
23.如图,四边形与四边形关于直线对称.
(1)点,,,的对称点分别是______,线段,的对称线段分别是______,______,______,______.
(2)与平行吗?为什么?
(3)若与平行,则能说明轴对称图形中对称点的连线一定互相平行吗?
24.如图,在平面直角坐标系中,A(﹣1,3)、B(﹣5,1)、C(﹣2,1).
(1)△ABC的面积为______.
(2)在图中作出△ABC关于x轴的对称图形△A1B1C1,并写出点A1的坐标.
(3)请说明△A2B2C2是由△A1B1C1经过怎样的变换得到的?
25.如图所示.
(1)作出关于轴对称的图形;
(2)在轴上确定一点,使得最小;
(3)求出的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.B
3.B
4.A
5.C
6.B
7.B
8.C
9.C
10.B
11.110°
12.70
13.70°/70度
14.AB⊥BC
15.五
16.105°
17.55
18. 3 等边三角形
19./40度
20.(-2,3)
21.(1)略
(2)
22.(1),(2);(3);(4)位置不改变,.
23.(1)E,F,G,H;EF,EH;GH;∠GFE;∠EHG;(2)AE∥BF;(3)AE与BF平行,不一定能说明轴对称图形对称点的连线互相平行,也有可能共线.
24.(1)3;(2)点A1的坐标为(﹣1,﹣3);(3)△A2B2C2是由△A1B1C1经过关于y轴对称得到.
25.(1)如图所示;(2)如图所示点P;(3);
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
