5.1物体位置的确定随堂练习-苏科版数学八年级上册(含答案)
文档属性
| 名称 | 5.1物体位置的确定随堂练习-苏科版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 23:10:02 | ||
图片预览


文档简介
5.1物体位置的确定随堂练习-苏科版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列不能准确表示地理位置的是( )
A.3排4号 B.东经125度,北纬43度
C.塔山东街666号 D.距巴川中学公交站100m
2.某天课间操时,嘉嘉、淇淇、小高的位置如图所示,嘉嘉对小高说:“如果我的位置用表示,淇淇的位置用表示,那么你的位置可以表示成什么?”( )
A. B. C. D.
3.周末,小明与小文相约一起到游乐园去游玩,如图是他俩在微信中的一段对话:
根据上面两人的对话纪录,小文能从M超市走到游乐园门口的路线是( )
A.向北直走700米,再向西直走300米
B.向北直走300米,再向西直走700米
C.向北直走500米,再向西直走200米
D.向南直走500米,再向西直走200米
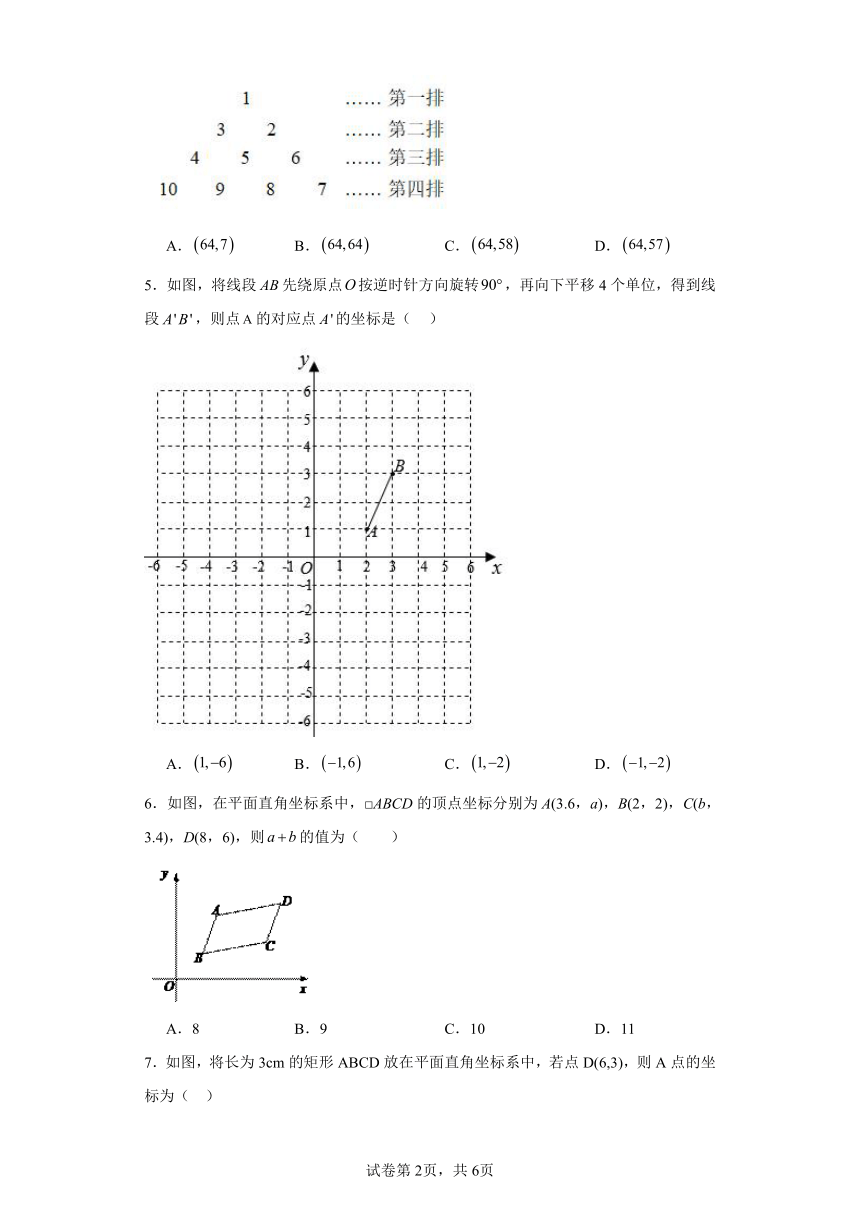
4.将正整数按如图所示的规律排列下去,若有序数对表示第n排,从左到右第m个数,如表示8,已知,则表示2023的有序数对是( )
A. B. C. D.
5.如图,将线段先绕原点按逆时针方向旋转,再向下平移4个单位,得到线段,则点的对应点的坐标是( )
A. B. C. D.
6.如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(3.6,a),B(2,2),C(b,3.4),D(8,6),则的值为( )
A.8 B.9 C.10 D.11
7.如图,将长为3cm的矩形ABCD放在平面直角坐标系中,若点D(6,3),则A点的坐标为( )
A. B. C. D.
8.某次大型活动由大学生组成仪仗队,若同学甲站在第六行第八列,可以表示为(6,8),则乙同学站第20行第7列,表示为( )
A.(7,20) B.(20,7) C.(7,7) D.(20,20)
9.如图,在平面直角坐标系上有点A(1.O),点A第一次跳动至点A1(-1,1).第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是( )
A.(50,49) B.(51, 49) C.(50, 50) D.(51, 50)
10.下列说法正确的是( ).
A.(2,3)和(3,2)表示的位置相同
B.(2,3)和(3,2)是表示不同位置的两个有序数
C.(2,2)和(2,2)表示两个不同的位置
D.(m,n)和(n,m)表示的位置不同
二、填空题
11.如图,以灯塔A为观测点,小岛B在灯塔A的北偏东45°方向上,距灯塔A 20 km处.若以小岛B为观测点,则灯塔A在小岛B的 方向上,距小岛B km处.
12.如果电影院中“5排7号”记作(5 ,7),那么(3,4)表示的意义是 .
13.如果将一张“13排10号”的电影票记为(13,10),那么“3排8号”的电影票应记为 ,(10,13)表示的电影票是 .
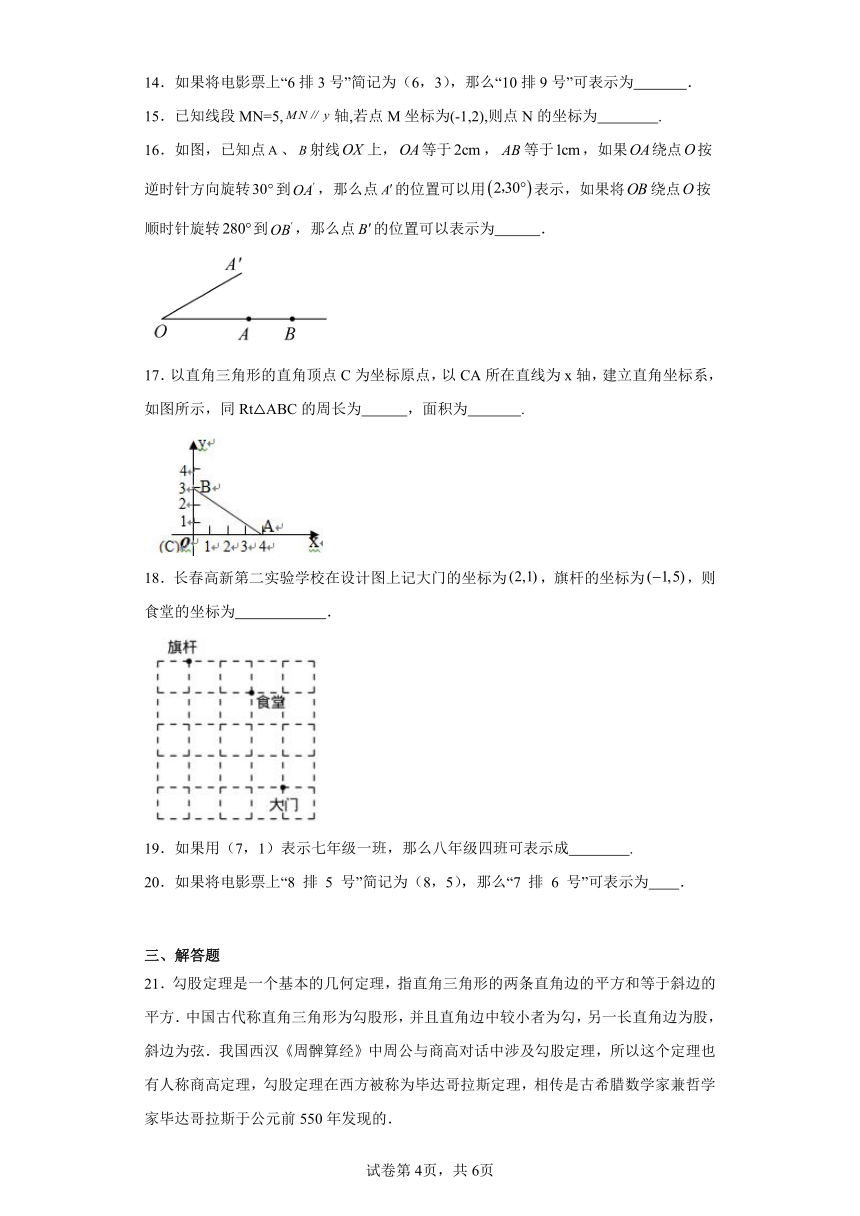
14.如果将电影票上“6排3号”简记为(6,3),那么“10排9号”可表示为 .
15.已知线段MN=5,轴,若点M坐标为(-1,2),则点N的坐标为 .
16.如图,已知点、射线上,等于,等于,如果绕点按逆时针方向旋转到,那么点的位置可以用表示,如果将绕点按顺时针旋转到,那么点的位置可以表示为 .
17.以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,同Rt△ABC的周长为 ,面积为 .
18.长春高新第二实验学校在设计图上记大门的坐标为,旗杆的坐标为,则食堂的坐标为 .
19.如果用(7,1)表示七年级一班,那么八年级四班可表示成 .
20.如果将电影票上“8 排 5 号”简记为(8,5),那么“7 排 6 号”可表示为 .
三、解答题
21.勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方.中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦.我国西汉《周髀算经》中周公与商高对话中涉及勾股定理,所以这个定理也有人称商高定理,勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的.
我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应.现在把这个数轴叫做x轴,同时,增加一个垂直于x轴的数轴,叫做y轴,如下图.这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A.若平面上的点M ,N ,我们定义点M、N在x轴方向上的距离为:,点M、N在y轴方向上的距离为:.例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5.
(1)若点B位置为(-1,-1),请在图中画出点B;图中点C的位置用数对______来表示.
(2)在(1)条件下,A、B两点在x轴方向上的距离为________,在y轴方向上的距离为_______,A、B两点间的距离为______;若E点、F点的位置分别为(a,b)、(c,d),点E、F之间的距离为|EF|,则=_______________.
(3)有一个点D,它与(0,0)点的距离为1,请画出D点所有可能的位置.
22.如图是某城市道路示意图:
(1)如果湘街与鲁路交叉道口点A的坐标记作,浙街与陕路交叉道口点B的坐标记作,则此时是______街与______路的交叉道口;
(2)在(1)的条件下渝街与陕路交叉道口的坐标记作______;沪街与京路交叉道口的坐标记作______;
(3)用有序数对写出2种从A地到B地的最短路线,如:—————.
23.如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?请分别写出这些路线.
24.如图所示,已知边长为1的正方形OABC在直角坐标系中,A、B两点在第一象限内,OA与x轴的夹角为,求点B的坐标.
25.如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.A
3.A
4.C
5.D
6.D
7.A
8.B
9.D
10.B
11. 南偏西45° 20
12.3排4号
13. (3,8) 10排13号
14.(10,9)
15.(-1,-3)或(-1,7).
16.
17. 12, 6
18.
19.(8,4)
20.(7,6)
21.(1)点C(4,5);(2)3,4,5;(a-c)+(b-d)(3)略.
22.(1)苏,冀
(2),
(3)略
23.①(2,4)→(4,4)→(4,2);②(2,4)→(3,4)→(3,2)→(4,2);③(2,4)→(4,3)→(3,3)→(4,3)→(4,2);④(2,4)→(2,3)→(4,3)→(4,2);⑤(2,4)→(2,2)→(4,2)
24.
25.(1);(2) ;(3)P(-3,) .
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列不能准确表示地理位置的是( )
A.3排4号 B.东经125度,北纬43度
C.塔山东街666号 D.距巴川中学公交站100m
2.某天课间操时,嘉嘉、淇淇、小高的位置如图所示,嘉嘉对小高说:“如果我的位置用表示,淇淇的位置用表示,那么你的位置可以表示成什么?”( )
A. B. C. D.
3.周末,小明与小文相约一起到游乐园去游玩,如图是他俩在微信中的一段对话:
根据上面两人的对话纪录,小文能从M超市走到游乐园门口的路线是( )
A.向北直走700米,再向西直走300米
B.向北直走300米,再向西直走700米
C.向北直走500米,再向西直走200米
D.向南直走500米,再向西直走200米
4.将正整数按如图所示的规律排列下去,若有序数对表示第n排,从左到右第m个数,如表示8,已知,则表示2023的有序数对是( )
A. B. C. D.
5.如图,将线段先绕原点按逆时针方向旋转,再向下平移4个单位,得到线段,则点的对应点的坐标是( )
A. B. C. D.
6.如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(3.6,a),B(2,2),C(b,3.4),D(8,6),则的值为( )
A.8 B.9 C.10 D.11
7.如图,将长为3cm的矩形ABCD放在平面直角坐标系中,若点D(6,3),则A点的坐标为( )
A. B. C. D.
8.某次大型活动由大学生组成仪仗队,若同学甲站在第六行第八列,可以表示为(6,8),则乙同学站第20行第7列,表示为( )
A.(7,20) B.(20,7) C.(7,7) D.(20,20)
9.如图,在平面直角坐标系上有点A(1.O),点A第一次跳动至点A1(-1,1).第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是( )
A.(50,49) B.(51, 49) C.(50, 50) D.(51, 50)
10.下列说法正确的是( ).
A.(2,3)和(3,2)表示的位置相同
B.(2,3)和(3,2)是表示不同位置的两个有序数
C.(2,2)和(2,2)表示两个不同的位置
D.(m,n)和(n,m)表示的位置不同
二、填空题
11.如图,以灯塔A为观测点,小岛B在灯塔A的北偏东45°方向上,距灯塔A 20 km处.若以小岛B为观测点,则灯塔A在小岛B的 方向上,距小岛B km处.
12.如果电影院中“5排7号”记作(5 ,7),那么(3,4)表示的意义是 .
13.如果将一张“13排10号”的电影票记为(13,10),那么“3排8号”的电影票应记为 ,(10,13)表示的电影票是 .
14.如果将电影票上“6排3号”简记为(6,3),那么“10排9号”可表示为 .
15.已知线段MN=5,轴,若点M坐标为(-1,2),则点N的坐标为 .
16.如图,已知点、射线上,等于,等于,如果绕点按逆时针方向旋转到,那么点的位置可以用表示,如果将绕点按顺时针旋转到,那么点的位置可以表示为 .
17.以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,同Rt△ABC的周长为 ,面积为 .
18.长春高新第二实验学校在设计图上记大门的坐标为,旗杆的坐标为,则食堂的坐标为 .
19.如果用(7,1)表示七年级一班,那么八年级四班可表示成 .
20.如果将电影票上“8 排 5 号”简记为(8,5),那么“7 排 6 号”可表示为 .
三、解答题
21.勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方.中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦.我国西汉《周髀算经》中周公与商高对话中涉及勾股定理,所以这个定理也有人称商高定理,勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的.
我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应.现在把这个数轴叫做x轴,同时,增加一个垂直于x轴的数轴,叫做y轴,如下图.这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A.若平面上的点M ,N ,我们定义点M、N在x轴方向上的距离为:,点M、N在y轴方向上的距离为:.例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5.
(1)若点B位置为(-1,-1),请在图中画出点B;图中点C的位置用数对______来表示.
(2)在(1)条件下,A、B两点在x轴方向上的距离为________,在y轴方向上的距离为_______,A、B两点间的距离为______;若E点、F点的位置分别为(a,b)、(c,d),点E、F之间的距离为|EF|,则=_______________.
(3)有一个点D,它与(0,0)点的距离为1,请画出D点所有可能的位置.
22.如图是某城市道路示意图:
(1)如果湘街与鲁路交叉道口点A的坐标记作,浙街与陕路交叉道口点B的坐标记作,则此时是______街与______路的交叉道口;
(2)在(1)的条件下渝街与陕路交叉道口的坐标记作______;沪街与京路交叉道口的坐标记作______;
(3)用有序数对写出2种从A地到B地的最短路线,如:—————.
23.如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?请分别写出这些路线.
24.如图所示,已知边长为1的正方形OABC在直角坐标系中,A、B两点在第一象限内,OA与x轴的夹角为,求点B的坐标.
25.如图,在下面直角坐标系中,已知A(0,2),B(3,0),C(3,4)三点,
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.A
3.A
4.C
5.D
6.D
7.A
8.B
9.D
10.B
11. 南偏西45° 20
12.3排4号
13. (3,8) 10排13号
14.(10,9)
15.(-1,-3)或(-1,7).
16.
17. 12, 6
18.
19.(8,4)
20.(7,6)
21.(1)点C(4,5);(2)3,4,5;(a-c)+(b-d)(3)略.
22.(1)苏,冀
(2),
(3)略
23.①(2,4)→(4,4)→(4,2);②(2,4)→(3,4)→(3,2)→(4,2);③(2,4)→(4,3)→(3,3)→(4,3)→(4,2);④(2,4)→(2,3)→(4,3)→(4,2);⑤(2,4)→(2,2)→(4,2)
24.
25.(1);(2) ;(3)P(-3,) .
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
