3.1勾股定理随堂练习(含答案)苏科版数学八年级上册
文档属性
| 名称 | 3.1勾股定理随堂练习(含答案)苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 528.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 21:48:51 | ||
图片预览


文档简介
3.1勾股定理随堂练习-苏科版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
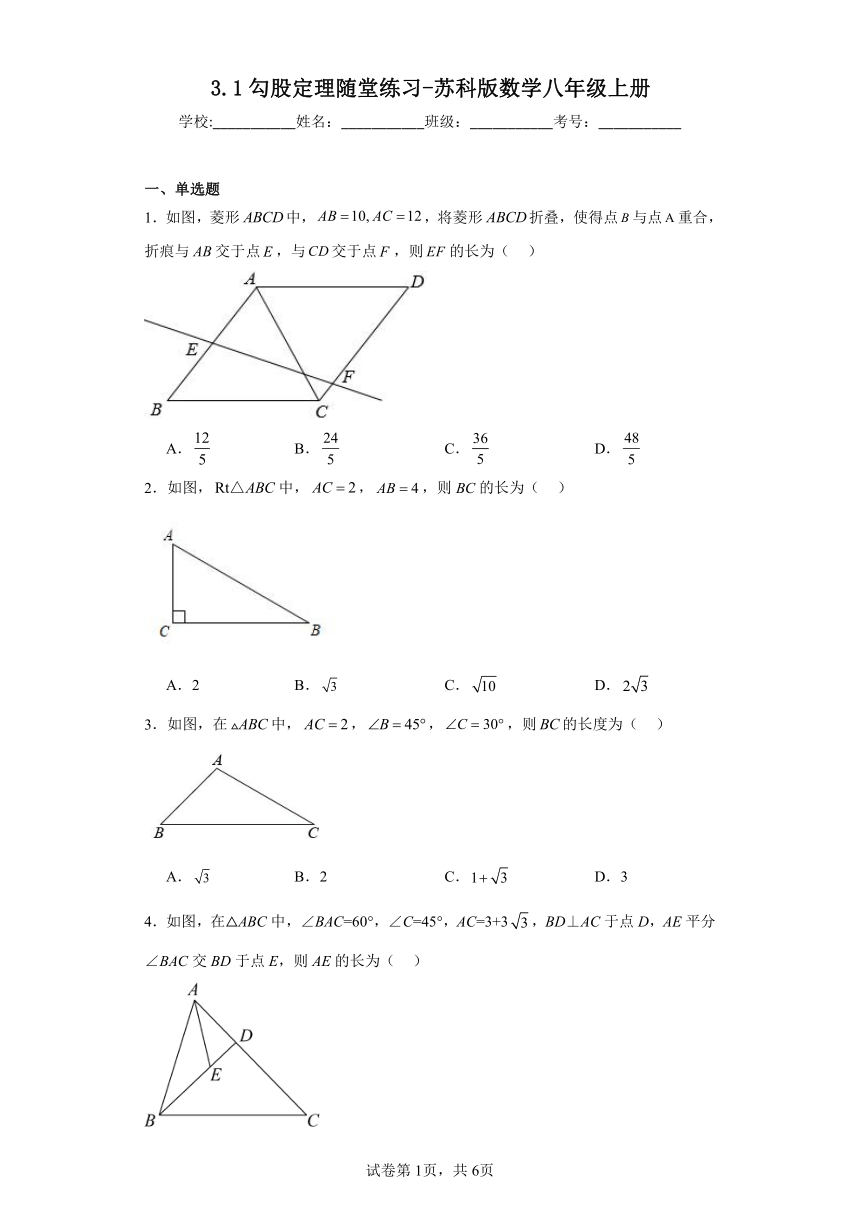
1.如图,菱形中,,将菱形折叠,使得点与点重合,折痕与交于点,与交于点,则的长为( )
A. B. C. D.
2.如图,中,,,则BC的长为( )
A.2 B. C. D.
3.如图,在中,,,,则的长度为( )
A. B.2 C. D.3
4.如图,在△ABC中,∠BAC=60°,∠C=45°,AC=3+3,BD⊥AC于点D,AE平分∠BAC交BD于点E,则AE的长为( )
A.5 B.2 C.3 D.4
5.在△ABC中AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42或32 D.38或32
6.在直角坐标系中,点P(﹣3,5)到原点的距离是( )
A.4 B. C. D.4或
7.在中,AD是BC边上的高,,则的面积为( )
A.18 B.24 C.18或24 D.18或30
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果大正方形的面积是5,小正方形的面积是1,直角三角形的两直角边长分别是a、,则的值为( )
A.16 B.9 C.4 D.3
9.如图,等边三角形ABC的周长为18,则BC边上的高AD的长为( )
A.3 B.3 C.6 D.6
10.如图,在中,,,分别以,为直角边作等腰直角三角形和等腰直角三角形.若的面积为,的面积为,则的结果为( )
A.25 B.10 C. D.
二、填空题
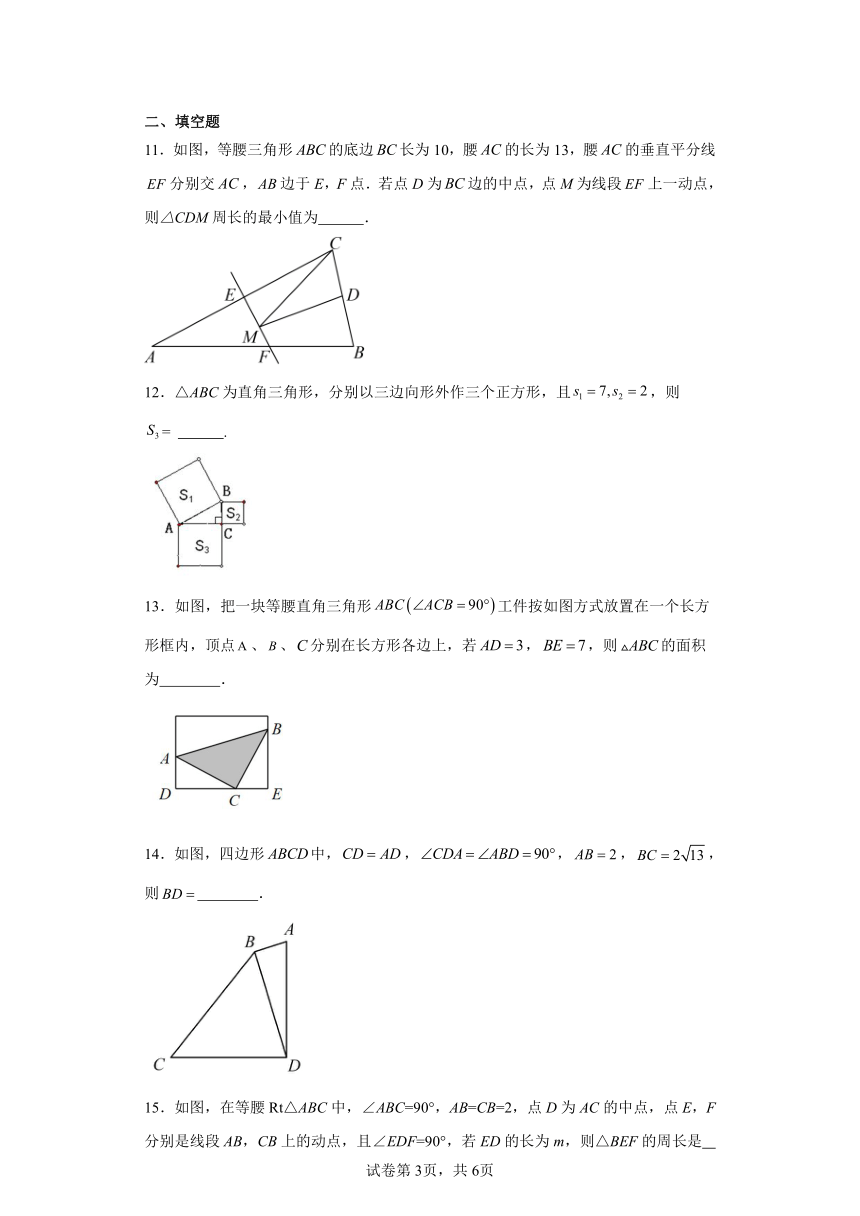
11.如图,等腰三角形的底边长为10,腰的长为13,腰的垂直平分线分别交,边于E,F点.若点D为边的中点,点M为线段上一动点,则△CDM周长的最小值为 .
12.△ABC为直角三角形,分别以三边向形外作三个正方形,且,则= .
13.如图,把一块等腰直角三角形工件按如图方式放置在一个长方形框内,顶点、、分别在长方形各边上,若,,则的面积为 .
14.如图,四边形中,,,,,则 .
15.如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是 (用含m的代数式表示)
16.我国古代数学家刘微将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形(,),如图所示,已知,,,则正方形的面积是 .
17.如图,在△ABC中,∠C=90°,BD是△ABC的角平分线,已知AC=3,BC=4,则CD的长为 .
18.在正方形中,点为边上一点且,点为对角线上一点且,连接交于点,过点作于点,连结、,若,则的面积是 .
19.如图,正的边长为2,以BC边上的高为边作正,与公共部分的面积记为;再以正边上的高为边作正,与公共部分的面积记为;…,以此类推,则 .
20.在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为 .
三、解答题
21.如图,在中,.
(1)利用直尺和圆规在边上找一点P,使得(保留作图痕迹,不写作法);
(2)在(1)的条件下,连接,若,,求线段的长.
22.在如图所示的方格图中,每个小方格的边长均为1,则的周长为多少?
23.如图1,放在墙角的立柜的上下底面是等腰直角三角形,如图2所示,若腰长为1m,现要将这个立柜搬过宽为0.8m的通道,你觉得能通过吗?请说明理由.
24.(1)问题发现:如图,和均为等边三角形,当旋转至点,,在同一直线上,连接.填空:
①的度数为 ;
②线段、之间的数量关系是 .
(2)拓展研究:如图,和均为等腰三角形,且,点、、在同一直线上,若,,,求、、之间的数量关系.
(3)探究发现:(1)题中图中的和,在旋转过程中当点,,不在同一直线上时,设直线与相交于点,试在备用图中探索的度数,直接写出结果,不必说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.D
3.C
4.B
5.C
6.C
7.D
8.B
9.B
10.C
11.
12.5
13.29
14.6
15./
16.4
17.
18.
19.
20..
21.(1)略
(2)5
22.
23.能
24.(1)①60°;②;(2);(3)的度数是或
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,菱形中,,将菱形折叠,使得点与点重合,折痕与交于点,与交于点,则的长为( )
A. B. C. D.
2.如图,中,,,则BC的长为( )
A.2 B. C. D.
3.如图,在中,,,,则的长度为( )
A. B.2 C. D.3
4.如图,在△ABC中,∠BAC=60°,∠C=45°,AC=3+3,BD⊥AC于点D,AE平分∠BAC交BD于点E,则AE的长为( )
A.5 B.2 C.3 D.4
5.在△ABC中AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42或32 D.38或32
6.在直角坐标系中,点P(﹣3,5)到原点的距离是( )
A.4 B. C. D.4或
7.在中,AD是BC边上的高,,则的面积为( )
A.18 B.24 C.18或24 D.18或30
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果大正方形的面积是5,小正方形的面积是1,直角三角形的两直角边长分别是a、,则的值为( )
A.16 B.9 C.4 D.3
9.如图,等边三角形ABC的周长为18,则BC边上的高AD的长为( )
A.3 B.3 C.6 D.6
10.如图,在中,,,分别以,为直角边作等腰直角三角形和等腰直角三角形.若的面积为,的面积为,则的结果为( )
A.25 B.10 C. D.
二、填空题
11.如图,等腰三角形的底边长为10,腰的长为13,腰的垂直平分线分别交,边于E,F点.若点D为边的中点,点M为线段上一动点,则△CDM周长的最小值为 .
12.△ABC为直角三角形,分别以三边向形外作三个正方形,且,则= .
13.如图,把一块等腰直角三角形工件按如图方式放置在一个长方形框内,顶点、、分别在长方形各边上,若,,则的面积为 .
14.如图,四边形中,,,,,则 .
15.如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是 (用含m的代数式表示)
16.我国古代数学家刘微将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形(,),如图所示,已知,,,则正方形的面积是 .
17.如图,在△ABC中,∠C=90°,BD是△ABC的角平分线,已知AC=3,BC=4,则CD的长为 .
18.在正方形中,点为边上一点且,点为对角线上一点且,连接交于点,过点作于点,连结、,若,则的面积是 .
19.如图,正的边长为2,以BC边上的高为边作正,与公共部分的面积记为;再以正边上的高为边作正,与公共部分的面积记为;…,以此类推,则 .
20.在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为 .
三、解答题
21.如图,在中,.
(1)利用直尺和圆规在边上找一点P,使得(保留作图痕迹,不写作法);
(2)在(1)的条件下,连接,若,,求线段的长.
22.在如图所示的方格图中,每个小方格的边长均为1,则的周长为多少?
23.如图1,放在墙角的立柜的上下底面是等腰直角三角形,如图2所示,若腰长为1m,现要将这个立柜搬过宽为0.8m的通道,你觉得能通过吗?请说明理由.
24.(1)问题发现:如图,和均为等边三角形,当旋转至点,,在同一直线上,连接.填空:
①的度数为 ;
②线段、之间的数量关系是 .
(2)拓展研究:如图,和均为等腰三角形,且,点、、在同一直线上,若,,,求、、之间的数量关系.
(3)探究发现:(1)题中图中的和,在旋转过程中当点,,不在同一直线上时,设直线与相交于点,试在备用图中探索的度数,直接写出结果,不必说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.D
3.C
4.B
5.C
6.C
7.D
8.B
9.B
10.C
11.
12.5
13.29
14.6
15./
16.4
17.
18.
19.
20..
21.(1)略
(2)5
22.
23.能
24.(1)①60°;②;(2);(3)的度数是或
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
