导数在实际问题中的应用(山东省荷泽地区菏泽市)
文档属性
| 名称 | 导数在实际问题中的应用(山东省荷泽地区菏泽市) |

|
|
| 格式 | rar | ||
| 文件大小 | 966.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-21 00:00:00 | ||
图片预览







文档简介
课件21张PPT。菏泽一中
管雨坤生活中的优化问题学习目标
1、能利用导数解决生活中的优化问题.
2、通过学习一些实际问题,体会数学建模的方法和导数在解题中的作用.
自主学习
1、生活中经常遇到求利润最大,用料最省,效率最高等问题,这些问题统称为优化问题.
2、利用导数解决优化问题的实质是利用导数求函数在闭区间上的最大值或最小值。
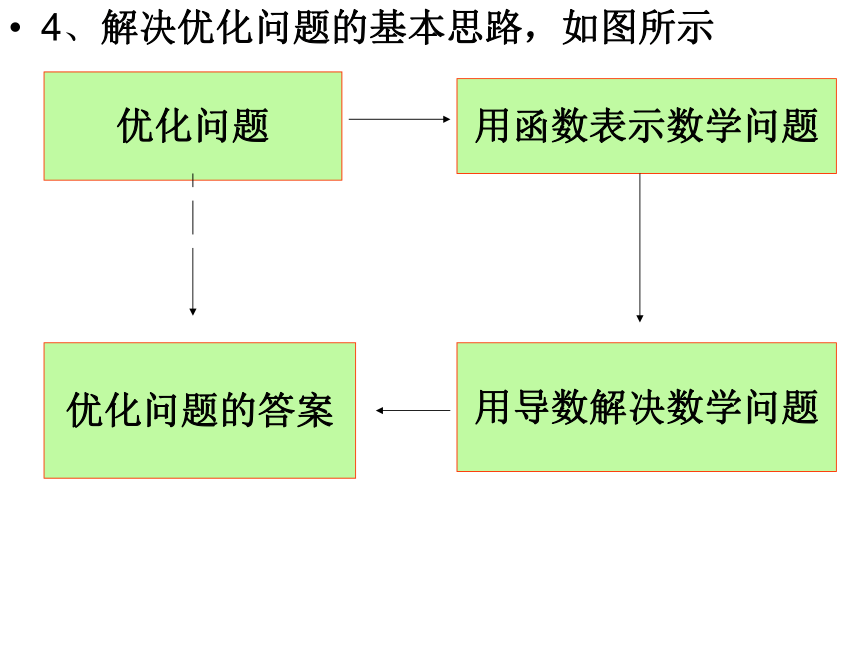
3、解决实际问题的关键在于建立数学模型和目标函数,把“问题情景”翻译为“数学语言”,找出问题的主要关系,抽象成数学问题,然后用可导函数求最值的方法求最值。 4、解决优化问题的基本思路,如图所示
优化问题用函数表示数学问题用导数解决数学问题优化问题的答案5、解决优化问题的步骤(1)分析实际问题中各量之间的关系,建立实际问题的数学模型,写出实际问题中各量之间的关系式
(2)求函数的导数 ,解方程
(3)比较函数在区间端点和极值,最大(小)者为最大(小)值。
(4)作答。
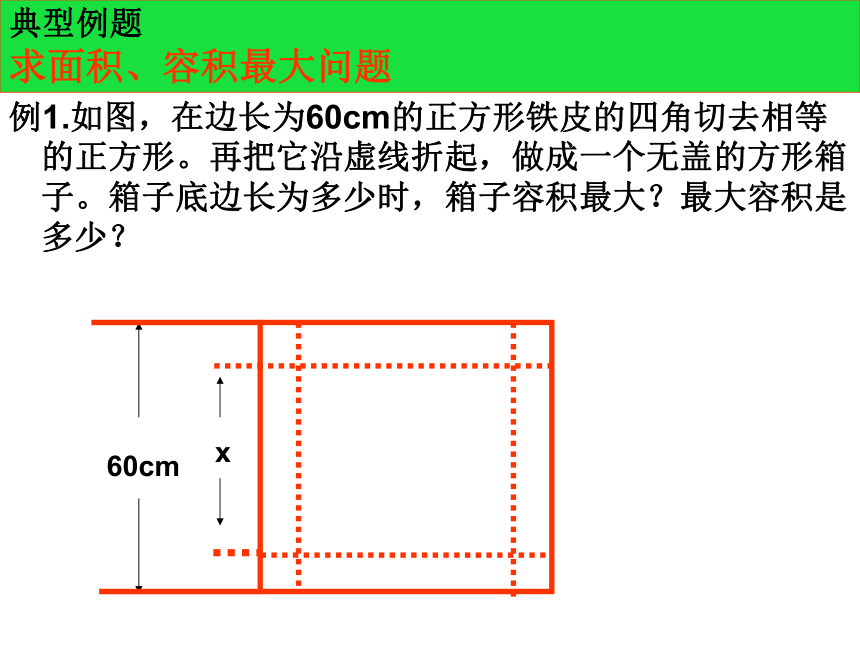
典型例题 求面积、容积最大问题例1.如图,在边长为60cm的正方形铁皮的四角切去相等的正方形。再把它沿虚线折起,做成一个无盖的方形箱子。箱子底边长为多少时,箱子容积最大?最大容积是多少?60cmx例1答案:如图,设箱底边长为x,则箱高 ,得箱子容
积V是箱底边长x的函数
令 ,解得 (舍)
,并求得 .有题意可知,当过小(接近0)或过大(接近60)时,,箱子容积很小,因此,16000是最大值。
答:当=40cm时,箱子容积最大,为16000 .用料最省问题例2.要设计一个容积为V的有盖圆柱形储油罐,已知侧面的单位面积造价是地面单位面积造价的一半;而盖的单位造价又是侧面的单位面积造价的一半;问储油罐的半径r和高h之比为何值时造价最省?例2答案:由 ,得
设盖的单位面积造价为a,则储油罐的造价为
令 ,解得 ,则
,由问题的实际意义,上述S的唯一可能极值点就是定义域上的最小值点。
答:当 时储油罐的造价最省。 费用最省问题例3.(2006年福建)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/时)的函数解析式为
已知甲、乙两地相距100千米。
(1)当汽车以40千米/时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少是多少升?解: (1)当x=40时,汽车从甲地到乙地行驶了 小时, 要耗油(.
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升. (2)当速度为x千米/小时,汽车从甲地到乙地行驶了
设耗油量为h(x)升,衣题意得
h(x)=( )·
h’(x)=(0<x≤120),令h’(x)=0,得x=80. 当x∈(0,80)时,h’(x)<0,h(x)是减函数; 当x∈(80,120)时,h’(x)>0,h(x)是增函数. ∴当x=80时,h(x)取到极小值h(80)=11.25. 因为h(x)在(0,120)上只有一个极值,所以它是最小值.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升拓展提高: 利润最大问题某生产饮料的企业拟投入适当的广告费对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为 已知生产此产品的年固定投入3万元,每生产1万件此产品需投入32万元。若每件售价为“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和。
(1)试将利润y(万元)表示为年广告费x(万元)的函数。如果年广告费投入100万元,企业是亏损还是盈利?
(2) 当年广告费投入多少万元时,企业年利润最大? 解(1)由题意,每年产销Q万件,共计成本32Q+3,销售收入[(32Q+3)*150%+x*50%]万元。
所以年利润y=(年收入)-(年成本)-(年广告费)
=
=
所以所求的函数关系式为
当x=100时,y<0,即当年广告费投入100万元时,企业亏损。(2)由 可得:
令 ,则
检测反馈 某工厂生产某种产品,已知该产品的月生产量x(吨) 与每吨产品的价格p(元/吨)之间的关系式为:
且生产x吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
. 解:每月生产x吨时的利润为 ,
故它就是最大值点,且最大值为:
答:每月生产200吨产品时利润达到最大,最大利润为315万元.本课小结1、生活中经常遇到求利润最大,用料最省,效率最高等问题,这些问题统称为优化问题.
2、利用导数解决优化问题的实质是利用导数求函数在闭区间上的最大值或最小值。
3、解决实际问题的关键在于建立数学模型和目标函数,把“问题情景”翻译为“数学语言”,找出问题的主要关系,抽象成数学问题,然后用可导函数求最值的方法求最值。
4、解决优化问题的步骤:
(1)分析实际问题中各量之间的关系,建立实际问题的数学模型,写出实际问题中各量之间的关系式
(2)求函数的导数,求出极值
(3)比较函数在区间端点和极值,最大(小)者为最大(小)值。
(4)作答。作业NO.15分形几何图片分形几何的图片
管雨坤生活中的优化问题学习目标
1、能利用导数解决生活中的优化问题.
2、通过学习一些实际问题,体会数学建模的方法和导数在解题中的作用.
自主学习
1、生活中经常遇到求利润最大,用料最省,效率最高等问题,这些问题统称为优化问题.
2、利用导数解决优化问题的实质是利用导数求函数在闭区间上的最大值或最小值。
3、解决实际问题的关键在于建立数学模型和目标函数,把“问题情景”翻译为“数学语言”,找出问题的主要关系,抽象成数学问题,然后用可导函数求最值的方法求最值。 4、解决优化问题的基本思路,如图所示
优化问题用函数表示数学问题用导数解决数学问题优化问题的答案5、解决优化问题的步骤(1)分析实际问题中各量之间的关系,建立实际问题的数学模型,写出实际问题中各量之间的关系式
(2)求函数的导数 ,解方程
(3)比较函数在区间端点和极值,最大(小)者为最大(小)值。
(4)作答。
典型例题 求面积、容积最大问题例1.如图,在边长为60cm的正方形铁皮的四角切去相等的正方形。再把它沿虚线折起,做成一个无盖的方形箱子。箱子底边长为多少时,箱子容积最大?最大容积是多少?60cmx例1答案:如图,设箱底边长为x,则箱高 ,得箱子容
积V是箱底边长x的函数
令 ,解得 (舍)
,并求得 .有题意可知,当过小(接近0)或过大(接近60)时,,箱子容积很小,因此,16000是最大值。
答:当=40cm时,箱子容积最大,为16000 .用料最省问题例2.要设计一个容积为V的有盖圆柱形储油罐,已知侧面的单位面积造价是地面单位面积造价的一半;而盖的单位造价又是侧面的单位面积造价的一半;问储油罐的半径r和高h之比为何值时造价最省?例2答案:由 ,得
设盖的单位面积造价为a,则储油罐的造价为
令 ,解得 ,则
,由问题的实际意义,上述S的唯一可能极值点就是定义域上的最小值点。
答:当 时储油罐的造价最省。 费用最省问题例3.(2006年福建)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/时)的函数解析式为
已知甲、乙两地相距100千米。
(1)当汽车以40千米/时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少是多少升?解: (1)当x=40时,汽车从甲地到乙地行驶了 小时, 要耗油(.
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升. (2)当速度为x千米/小时,汽车从甲地到乙地行驶了
设耗油量为h(x)升,衣题意得
h(x)=( )·
h’(x)=(0<x≤120),令h’(x)=0,得x=80. 当x∈(0,80)时,h’(x)<0,h(x)是减函数; 当x∈(80,120)时,h’(x)>0,h(x)是增函数. ∴当x=80时,h(x)取到极小值h(80)=11.25. 因为h(x)在(0,120)上只有一个极值,所以它是最小值.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升拓展提高: 利润最大问题某生产饮料的企业拟投入适当的广告费对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为 已知生产此产品的年固定投入3万元,每生产1万件此产品需投入32万元。若每件售价为“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和。
(1)试将利润y(万元)表示为年广告费x(万元)的函数。如果年广告费投入100万元,企业是亏损还是盈利?
(2) 当年广告费投入多少万元时,企业年利润最大? 解(1)由题意,每年产销Q万件,共计成本32Q+3,销售收入[(32Q+3)*150%+x*50%]万元。
所以年利润y=(年收入)-(年成本)-(年广告费)
=
=
所以所求的函数关系式为
当x=100时,y<0,即当年广告费投入100万元时,企业亏损。(2)由 可得:
令 ,则
检测反馈 某工厂生产某种产品,已知该产品的月生产量x(吨) 与每吨产品的价格p(元/吨)之间的关系式为:
且生产x吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
. 解:每月生产x吨时的利润为 ,
故它就是最大值点,且最大值为:
答:每月生产200吨产品时利润达到最大,最大利润为315万元.本课小结1、生活中经常遇到求利润最大,用料最省,效率最高等问题,这些问题统称为优化问题.
2、利用导数解决优化问题的实质是利用导数求函数在闭区间上的最大值或最小值。
3、解决实际问题的关键在于建立数学模型和目标函数,把“问题情景”翻译为“数学语言”,找出问题的主要关系,抽象成数学问题,然后用可导函数求最值的方法求最值。
4、解决优化问题的步骤:
(1)分析实际问题中各量之间的关系,建立实际问题的数学模型,写出实际问题中各量之间的关系式
(2)求函数的导数,求出极值
(3)比较函数在区间端点和极值,最大(小)者为最大(小)值。
(4)作答。作业NO.15分形几何图片分形几何的图片
