第一章勾股定理单元复习题(含解析)2023-2024学年北师大版八年级数学上册
文档属性
| 名称 | 第一章勾股定理单元复习题(含解析)2023-2024学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 592.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 21:46:01 | ||
图片预览

文档简介
北师大版八年级数学上册第一章勾股定理单元复习题
一、选择题
1.在中,,,,则的长为( )
A.5 B.10 C. D.28
2.一个直角三角形的两边长分别为4cm、3cm,则第三条边长为( )
A.5cm B.4cm C.cm D.5cm 或cm
3.已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )
A. B.,,
C. D.
4.以下列各组数为边长,能构成直角三角形的是( )
A.,,2 B.1,2, C.1,, D.4,5,6
5.如图,一根长为的竹竿斜靠在竖直的墙壁上,竹竿底端B离墙壁距离,则该竹竿的顶端A离地竖直高度为( )
A. B. C. D.
6.如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为( )
A.2 B.4 C.3 D.1+2
7.如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.9 B.35 C.45 D.无法计算
8.在△ABC中,a,b,c分别是,,的对边,下列不能确定为直角三角形的是( )
A. B.
C. D.
9.如图折叠直角三角形纸片,使直角边落在斜边上折痕为,点落到点处,已知,,,则的长是( )
A.3 B.4 C.5 D.6
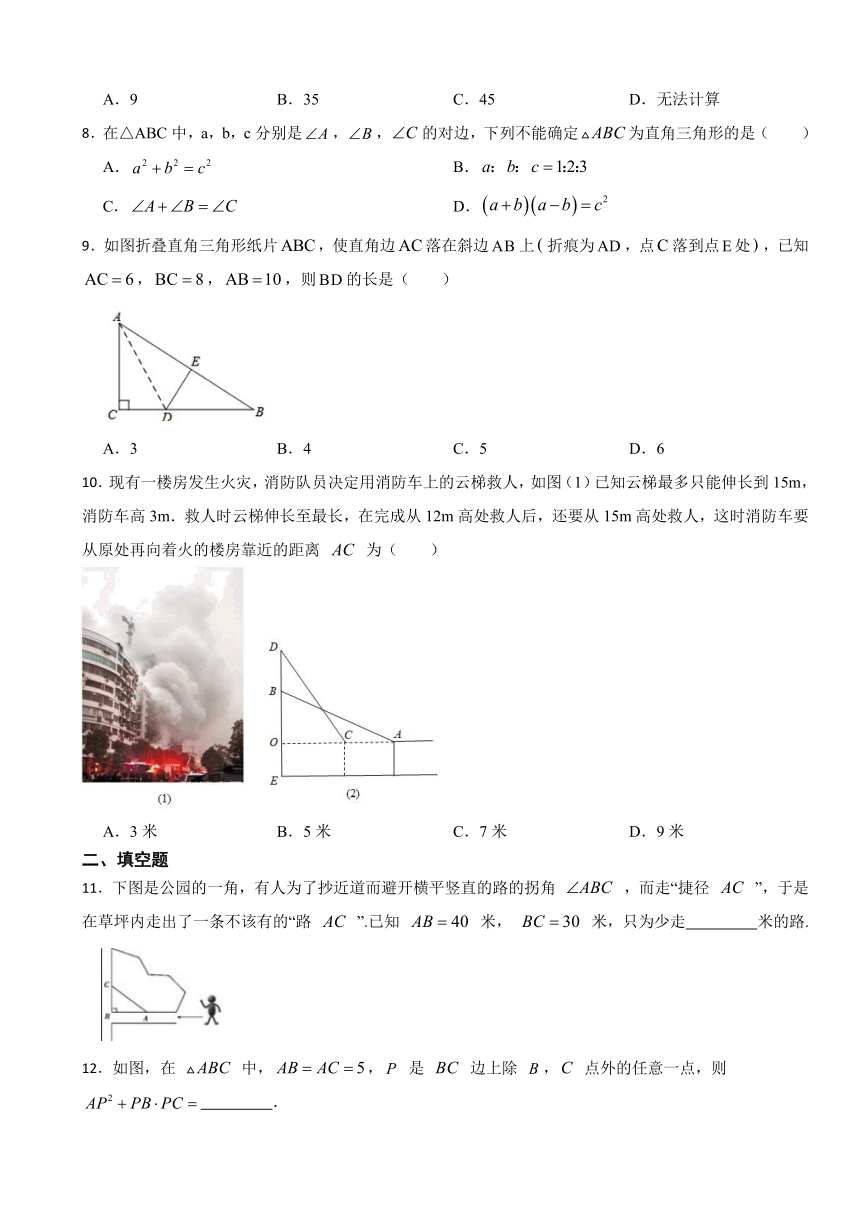
10.现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图(1)已知云梯最多只能伸长到15m,消防车高3m.救人时云梯伸长至最长,在完成从12m高处救人后,还要从15m高处救人,这时消防车要从原处再向着火的楼房靠近的距离 为( )
A.3米 B.5米 C.7米 D.9米
二、填空题
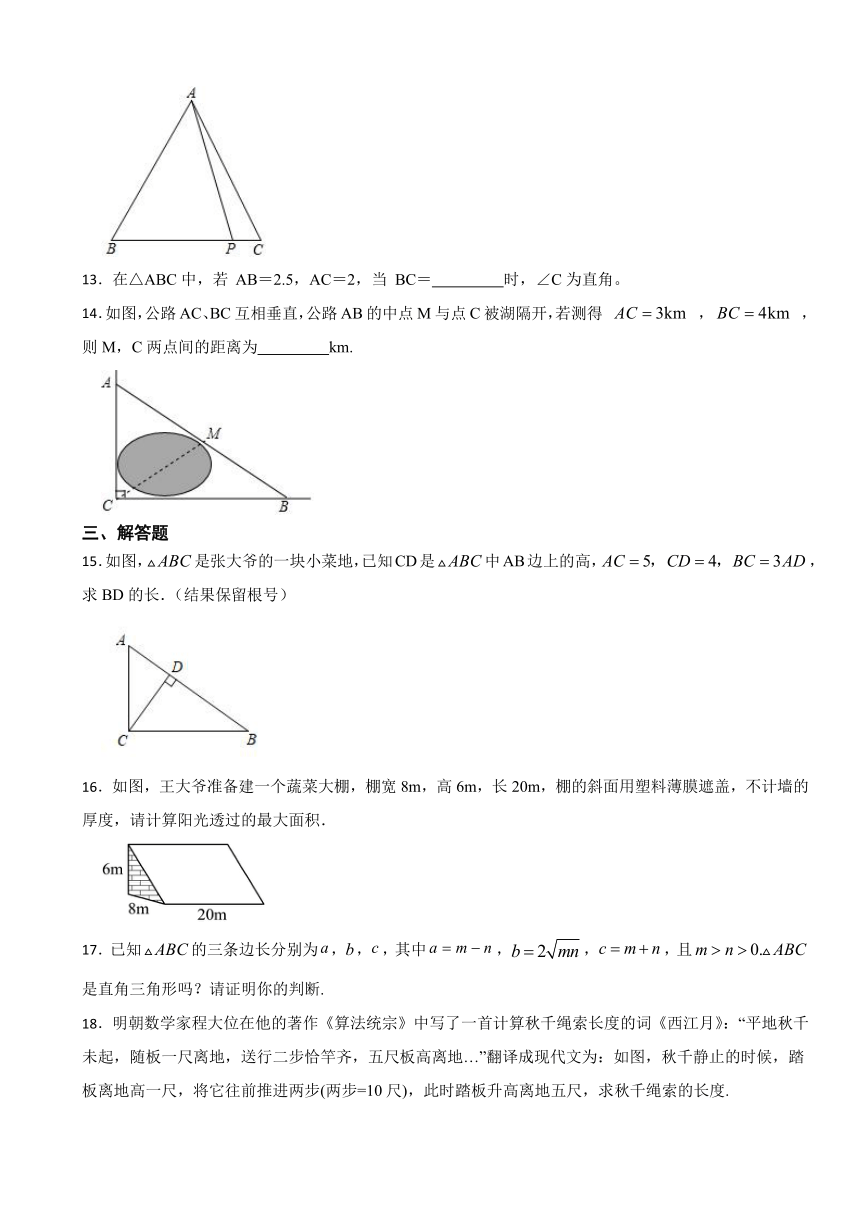
11.下图是公园的一角,有人为了抄近道而避开横平竖直的路的拐角 ,而走“捷径 ”,于是在草坪内走出了一条不该有的“路 ”.已知 米, 米,只为少走 米的路.
12.如图,在 中,, 是 边上除 , 点外的任意一点,则 .
13.在△ABC中,若 AB=2.5,AC=2,当 BC= 时,∠C为直角。
14.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 , ,则M,C两点间的距离为 km.
三、解答题
15.如图,是张大爷的一块小菜地,已知CD是中AB边上的高,,求BD的长.(结果保留根号)
16.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
17.已知的三条边长分别为,,,其中,,,且是直角三角形吗?请证明你的判断.
18.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,随板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺,将它往前推进两步(两步=10尺),此时踏板升高离地五尺,求秋千绳索的长度.
四、综合题
19.如图,在中,,平分交于点D,作于点E.
(1)若,求的度数;
(2)若,,求的面积.
20.如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=12,BD=5.
(1)求证:△BDC是直角三角形;
(2)求AC的长.
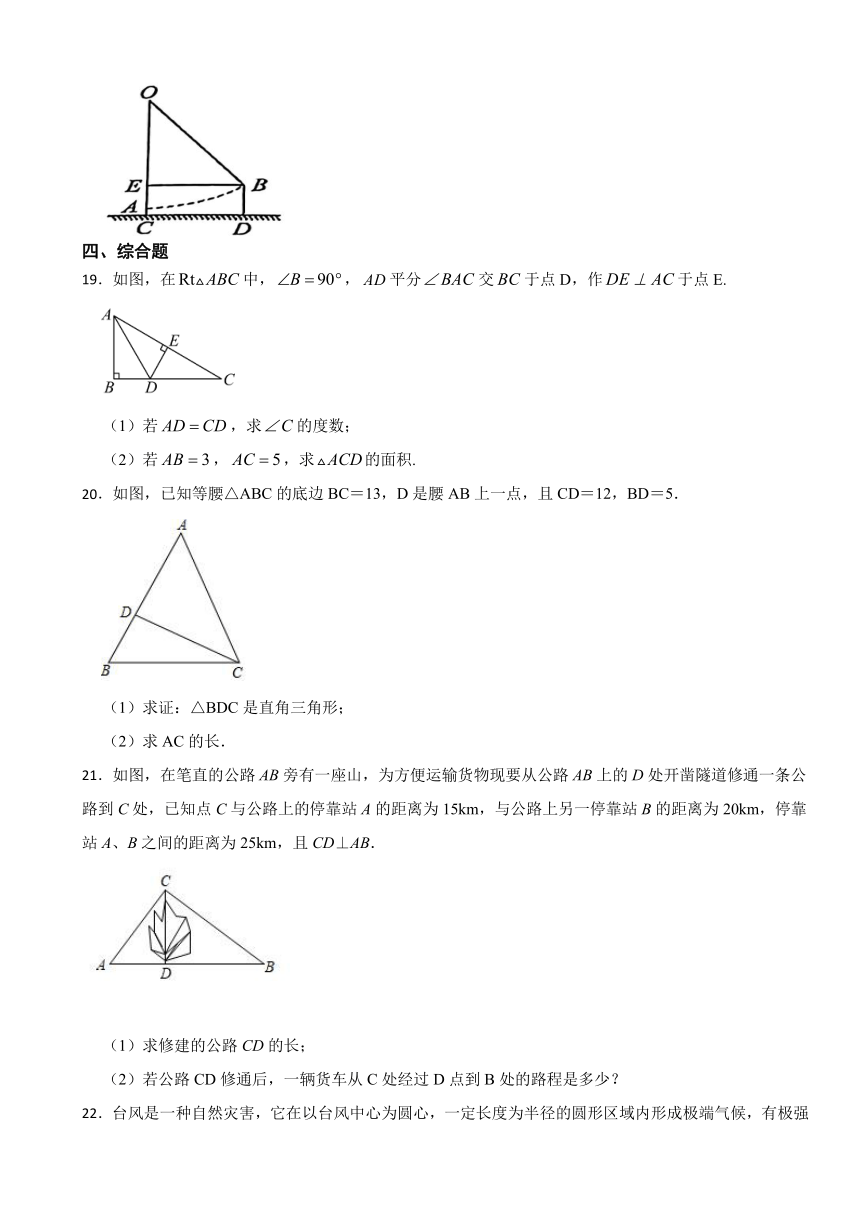
21.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
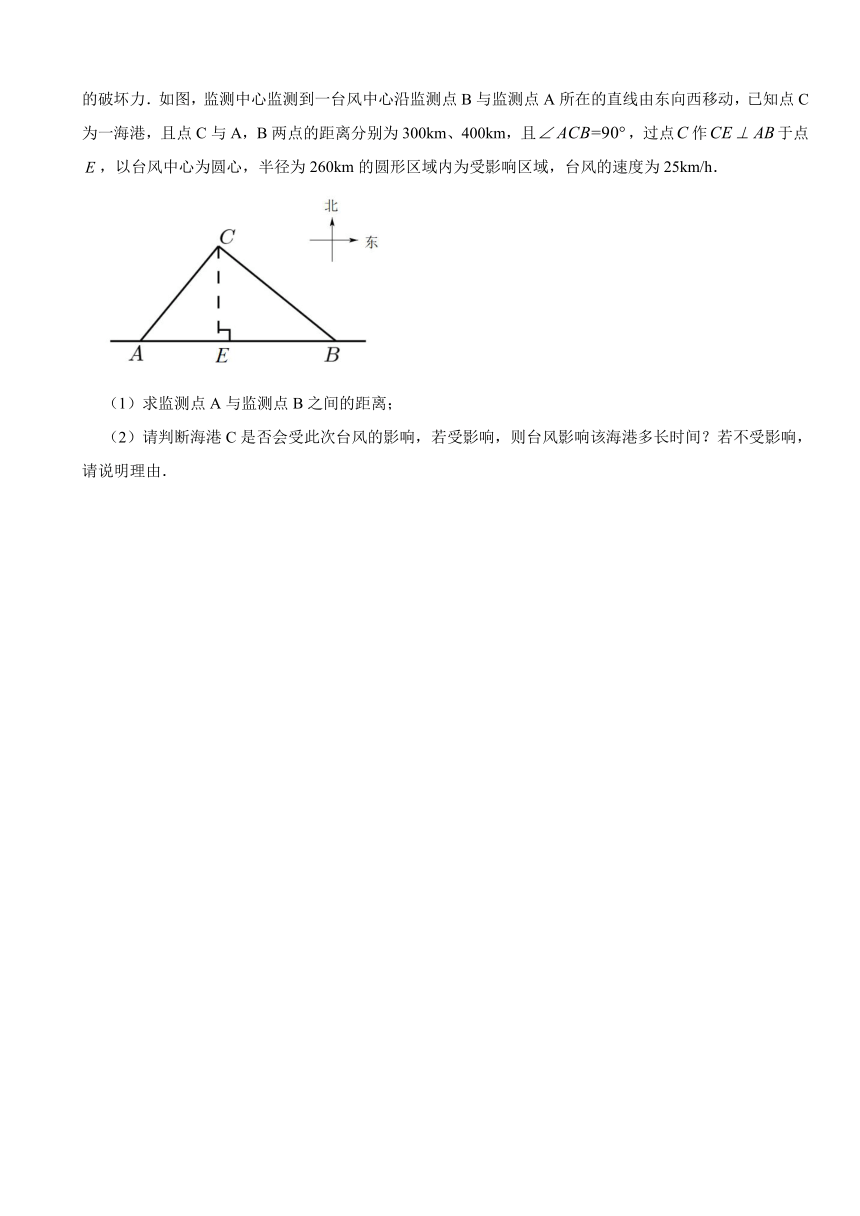
22.台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为300km、400km,且,过点作于点,以台风中心为圆心,半径为260km的圆形区域内为受影响区域,台风的速度为25km/h.
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,若受影响,则台风影响该海港多长时间?若不受影响,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】解:∵在中,,,,
∴,
故答案为:B.
【分析】根据题意,利用勾股定理计算求解即可。
2.【答案】D
【解析】【解答】解:①当两边均为直角边时,由勾股定理得,第三边为5cm;
②当4为斜边时,由勾股定理得,第三边为 cm;
故直角三角形的第三边应该为5cm或 cm.
故答案为:D.
【分析】此题分类讨论:①当两边均为直角边时,②当4为斜边时,分别根据勾股定理算出第三边的长.
3.【答案】D
【解析】【解答】解:∵,
∴,
∴是直角三角形,故A不符合题意;
∵,,
∴,
∴是直角三角形,故B不符合题意;
∵,,
∴,
∴,
∴是直角三角形,故C不符合题意;
∵,,
∴,
∴不是直角三角形,故D符合题意;
故答案为:D.
【分析】根据勾股定理的逆定理,如果一个三角形的三边满足较小两边的平方和等于最大边长的平方,那么这个三角形就是直角三角形,据此可判断A、B选项;根据三角形的内角和定理算出最大内角的度数,如果等于90°就是直角三角形,否则就不是,据此可判断C、D选项.
4.【答案】C
【解析】【解答】解:A、,故此选项中的三条线段不能构成直角三角形;
B、,故此选项中的三条线段不能构成直角三角形;
C、,故此选项中的三条线段能构成直角三角形;
D、,故此选项中的三条线段不能构成直角三角形.
故答案为:C.
【分析】如果一个三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形就是直角三角形,据此一一判断得出答案.
5.【答案】C
【解析】【解答】解:由题意得:,,,
则,
即该竹竿的顶端A离地竖直高度为,
故答案为:C.
【分析】直角利用勾股定理计算即可.
6.【答案】A
【解析】【解答】解:连接BE交AD于点M,连接CM,过点E作EH⊥BC于点H,
∴∠EHC=∠BHE=90°,
∵△ABC是等边三角形,AD是BC边的中线,
∴AD⊥BC,BD=CD,
∴点B,C关于AD对称,
∴BM=CM,
∴EM+CM=BM+ME=BE,
两点之间线段最短,此时EM+CM的最小值就是BE的长,
∵△ABC是等边三角形,AE=2,BC=AC=6,
∴CE=4,∠ECH=60°,∠CEH=90°-60°=30°,
∴,
∴BH=6-2=4,
∴;
在Rt△BEH中
.
故答案为:A
【分析】连接BE交AD于点M,连接CM,过点E作EH⊥BC于点H,利用垂直的定义可证得∠EHC=∠BHE=90°,利用等边三角形的性质可得到点B,C关于AD对称,利用轴对称的性质可推出MB=CM,利用两点之间线段最短,可知EM+CM的最小值就是BE的长;利用等边三角形的性质可证得CE=4,∠ECH=60°,∠CEH=30°,利用30°角所对的直角边等于斜边的一半,可求出CH的长,同时求出BH的长,利用勾股定理求出EH的长;然后利用勾股定理求出BE的长.
7.【答案】C
【解析】【解答】解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AB2=AD2+BD2,AC2=AD2+DC2,
∴AC2-AB2=DC2-BD2=81-36=45;
∵MC2=CD2+DM2,BM2=BD2+DM2,
∴MC2-MB2=DC2-BD2=45.
故答案为:C
【分析】利用垂直的定义可证得∠ADB=∠ADC=90°,利用勾股定理可证得AB2=AD2+BD2,AC2=AD2+DC2,可求出DC2-BD2的值;利用勾股定理可得到MC2=CD2+DM2,BM2=BD2+DM2,从而可求出MC2-MB2的值.
8.【答案】B
【解析】【解答】解:因为 ,
所以能判断△ABC为直角三角形,
故A不符合题意;
因为 ,
设 ,
则
所以不能判断△ABC为直角三角形,
故B符合题意;
因为 ,
所以
所以能判断△ABC为直角三角形,
故C不符合题意;
因为 ,
所以
所以能判断△ABC为直角三角形,
故D不符合题意;
故答案为:B.
【分析】根据勾股定理的逆定理,一个三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形就是直角三角形,据此判断A、B、D;根据三角形的内角和定理及有一个角是直角的三角形就是直角三角形可判断C.
9.【答案】C
【解析】【解答】解:,,,
由勾股定理逆定理得:.
由折叠的性质知,,,.
,
在中,由勾股定理得,
即,
解得:.
.
故答案为:C.
【分析】由勾股定理逆定理得∠ACB=90°,由折叠的性质知AE=AC=6,DE=CD,∠AED=∠C=90°,则BE=AB-AE=4,在Rt△BDE中,根据勾股定理可得CD的值,进而可得BD.
10.【答案】A
【解析】【解答】解:如图所示: m, m, m, m,
在 中,
m,
在 中,
m,
∴ m,
故答案为:A.
【分析】先利用勾股定理求出AO和CO的长,再利用线段的和差列出算式求解即可。
11.【答案】20
【解析】【解答】解:在Rt△ABC中,AB=40m,BC=30m,则:AC= =50m
所以少走的路为40+30-50=20m.
故答案为:20 .
【分析】先用勾股定理求出AC的长,然后用AB+BC-AC求出少走的路即可.
12.【答案】25
【解析】【解答】解:如图,过点A作于点D,
∵,,
∴,,,
∴
.
故答案为:25.
【分析】过点A作于点D,利用勾股定理及等量代换可得。
13.【答案】1.5
【解析】【解答】解:如图,
由∠C为直角得到BC=
故答案为:1.5.
【分析】根据勾股定理即可求解.
14.【答案】2.5
【解析】【解答】解:∵公路AC,BC互相垂直,
∴∠ACB=90°,
∵ , ,
在Rt△ABC中,
根据勾股定理AB= km
∵M为AB的中点,
∴CM= km,
即M,C两点间的距离为2.5km,
故答案为:2.5.
【分析】在Rt△ABC中,根据勾股定理求出AB长,再根据三角形斜边中线的性质,即可作答.
15.【答案】解:∵CD是中AB边上的高,
∴△ACD和△BCD都是直角三角形.
在Rt△ACD中
∴,
∵,
∴,
在Rt△BCD中,
.
【解析】【分析】先求出 △ACD和△BCD都是直角三角形,再利用勾股定理求出AD=3,最后利用勾股定理计算求解即可。
16.【答案】解:根据勾股定理得,蔬菜大棚的斜面的宽度即直角三角形的斜边长为:
,
所以蔬菜大棚的斜面面积为:10×20=200.
答:阳光透过的最大面积为200.
【解析】【分析】根据勾股定理得:蔬菜大棚的斜面的宽度即直角三角形的斜边长为10,然后根据矩形的面积公式进行计算.
17.【答案】解:的三条边长分别为,,,,,,
,
是直角三角形.
【解析】【分析】根据已知条件可得a2+b2=(m-n)2+4mn=(m+n)2,c2=(m+n)2,然后结合勾股定理逆定理进行解答.
18.【答案】解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺.
∴EA=EC-AC=5-1=4(尺),
OE=OA-AE=(x-4)尺,
在Rt△OEB中,OE=(x-4)尺,OB=x尺,EB=10尺.
根据勾股定理得:x2=﹙x-4﹚2+102,
整理得:8x=116,
即2x=29,
解得:x=14.5,
答:秋千绳索的长度是l4.5尺.
【解析】【分析】设OA=OB=x尺,根据已知条件,表示出OE,在Rt△OEB中,根据勾股定理列方程,解方程即可.
19.【答案】(1)解:平分,
,
,
,
,
,
,
;
(2)解:平分,,,
,
,
,
,,
,,,
,
设,
,
,
,
解得,
,
的面积为:
.
【解析】【分析】(1)根据角平分线的概念可得∠BAD=∠CAD,由等腰三角形的性质可得∠CAD=∠C,则∠BAD=∠CAD=∠C,∠BAC=2∠C,由∠BAC+∠C=90°可得∠C的度数;
(2)根据角平分线的性质可得DB=DE,利用HL证明△ABD≌△AED,由全等三角形的性质可得AE=AB=3,CE=AC-AE=2,利用勾股定理可求出BC的值,设BD=DE=x,则CD=4-x,然后在Rt△CDE中,根据勾股定理求出x的值,接下来根据三角形的面积公式进行计算.
20.【答案】(1)证明:∵BC=13,CD=12,BD=5,52+122=132,
∴BC2=BD2+CD2,
∴△BDC为直角三角形;
(2)解:设AB=x,
∵△ABC是等腰三角形,
∴AB=AC=x,
∵AC2=AD2+CD2,
即x2=(x﹣5)2+122,
解得:x=16.9,
∴AC=16.9.
【解析】【分析】(1)由BC=13,CD=12,BD=5,得出BC2=BD2+CD2,即可得出△BDC为直角三角形;
(2)由(1)可求出AC的长。
21.【答案】(1)解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
【解析】【分析】(1)先利用勾股定理的逆定理可得△ACB是直角三角形,∠ACB=90°,再结合三角形的面积求出CD的长即可;
(2)先利用勾股定理求出BD的长,再利用线段的和差求解即可。
22.【答案】(1)解:在中,km,km,
(km),
答:监测点与监测点之间的距离为500km;
(2)解:海港受台风影响,
理由:,,
,
,
km,
以台风中心为圆心周围260km以内为受影响区域,
海港会受到此次台风的影响,
以为圆心,260km长为半径画弧,交于,,
则km时,正好影响港口,
在中,
(km),
km,
台风的速度为25千米小时,
(小时).
答:台风影响该海港持续的时间为8小时.
【解析】【分析】(1)利用勾股定理计算即可;
(2) 海港受台风影响,理由:利用三角形的面积公式可求出CE的长,与260km进行比较,可得出 海港受台风影响; 以为圆心,260km长为半径画弧,交于,, 则DE=EF=260km,利用勾股定理求出DE,进而求出DF的长,根据时间=路程÷速度即可求解.
一、选择题
1.在中,,,,则的长为( )
A.5 B.10 C. D.28
2.一个直角三角形的两边长分别为4cm、3cm,则第三条边长为( )
A.5cm B.4cm C.cm D.5cm 或cm
3.已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )
A. B.,,
C. D.
4.以下列各组数为边长,能构成直角三角形的是( )
A.,,2 B.1,2, C.1,, D.4,5,6
5.如图,一根长为的竹竿斜靠在竖直的墙壁上,竹竿底端B离墙壁距离,则该竹竿的顶端A离地竖直高度为( )
A. B. C. D.
6.如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为( )
A.2 B.4 C.3 D.1+2
7.如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.9 B.35 C.45 D.无法计算
8.在△ABC中,a,b,c分别是,,的对边,下列不能确定为直角三角形的是( )
A. B.
C. D.
9.如图折叠直角三角形纸片,使直角边落在斜边上折痕为,点落到点处,已知,,,则的长是( )
A.3 B.4 C.5 D.6
10.现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图(1)已知云梯最多只能伸长到15m,消防车高3m.救人时云梯伸长至最长,在完成从12m高处救人后,还要从15m高处救人,这时消防车要从原处再向着火的楼房靠近的距离 为( )
A.3米 B.5米 C.7米 D.9米
二、填空题
11.下图是公园的一角,有人为了抄近道而避开横平竖直的路的拐角 ,而走“捷径 ”,于是在草坪内走出了一条不该有的“路 ”.已知 米, 米,只为少走 米的路.
12.如图,在 中,, 是 边上除 , 点外的任意一点,则 .
13.在△ABC中,若 AB=2.5,AC=2,当 BC= 时,∠C为直角。
14.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 , ,则M,C两点间的距离为 km.
三、解答题
15.如图,是张大爷的一块小菜地,已知CD是中AB边上的高,,求BD的长.(结果保留根号)
16.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
17.已知的三条边长分别为,,,其中,,,且是直角三角形吗?请证明你的判断.
18.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,随板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺,将它往前推进两步(两步=10尺),此时踏板升高离地五尺,求秋千绳索的长度.
四、综合题
19.如图,在中,,平分交于点D,作于点E.
(1)若,求的度数;
(2)若,,求的面积.
20.如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=12,BD=5.
(1)求证:△BDC是直角三角形;
(2)求AC的长.
21.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
22.台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为300km、400km,且,过点作于点,以台风中心为圆心,半径为260km的圆形区域内为受影响区域,台风的速度为25km/h.
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,若受影响,则台风影响该海港多长时间?若不受影响,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】解:∵在中,,,,
∴,
故答案为:B.
【分析】根据题意,利用勾股定理计算求解即可。
2.【答案】D
【解析】【解答】解:①当两边均为直角边时,由勾股定理得,第三边为5cm;
②当4为斜边时,由勾股定理得,第三边为 cm;
故直角三角形的第三边应该为5cm或 cm.
故答案为:D.
【分析】此题分类讨论:①当两边均为直角边时,②当4为斜边时,分别根据勾股定理算出第三边的长.
3.【答案】D
【解析】【解答】解:∵,
∴,
∴是直角三角形,故A不符合题意;
∵,,
∴,
∴是直角三角形,故B不符合题意;
∵,,
∴,
∴,
∴是直角三角形,故C不符合题意;
∵,,
∴,
∴不是直角三角形,故D符合题意;
故答案为:D.
【分析】根据勾股定理的逆定理,如果一个三角形的三边满足较小两边的平方和等于最大边长的平方,那么这个三角形就是直角三角形,据此可判断A、B选项;根据三角形的内角和定理算出最大内角的度数,如果等于90°就是直角三角形,否则就不是,据此可判断C、D选项.
4.【答案】C
【解析】【解答】解:A、,故此选项中的三条线段不能构成直角三角形;
B、,故此选项中的三条线段不能构成直角三角形;
C、,故此选项中的三条线段能构成直角三角形;
D、,故此选项中的三条线段不能构成直角三角形.
故答案为:C.
【分析】如果一个三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形就是直角三角形,据此一一判断得出答案.
5.【答案】C
【解析】【解答】解:由题意得:,,,
则,
即该竹竿的顶端A离地竖直高度为,
故答案为:C.
【分析】直角利用勾股定理计算即可.
6.【答案】A
【解析】【解答】解:连接BE交AD于点M,连接CM,过点E作EH⊥BC于点H,
∴∠EHC=∠BHE=90°,
∵△ABC是等边三角形,AD是BC边的中线,
∴AD⊥BC,BD=CD,
∴点B,C关于AD对称,
∴BM=CM,
∴EM+CM=BM+ME=BE,
两点之间线段最短,此时EM+CM的最小值就是BE的长,
∵△ABC是等边三角形,AE=2,BC=AC=6,
∴CE=4,∠ECH=60°,∠CEH=90°-60°=30°,
∴,
∴BH=6-2=4,
∴;
在Rt△BEH中
.
故答案为:A
【分析】连接BE交AD于点M,连接CM,过点E作EH⊥BC于点H,利用垂直的定义可证得∠EHC=∠BHE=90°,利用等边三角形的性质可得到点B,C关于AD对称,利用轴对称的性质可推出MB=CM,利用两点之间线段最短,可知EM+CM的最小值就是BE的长;利用等边三角形的性质可证得CE=4,∠ECH=60°,∠CEH=30°,利用30°角所对的直角边等于斜边的一半,可求出CH的长,同时求出BH的长,利用勾股定理求出EH的长;然后利用勾股定理求出BE的长.
7.【答案】C
【解析】【解答】解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AB2=AD2+BD2,AC2=AD2+DC2,
∴AC2-AB2=DC2-BD2=81-36=45;
∵MC2=CD2+DM2,BM2=BD2+DM2,
∴MC2-MB2=DC2-BD2=45.
故答案为:C
【分析】利用垂直的定义可证得∠ADB=∠ADC=90°,利用勾股定理可证得AB2=AD2+BD2,AC2=AD2+DC2,可求出DC2-BD2的值;利用勾股定理可得到MC2=CD2+DM2,BM2=BD2+DM2,从而可求出MC2-MB2的值.
8.【答案】B
【解析】【解答】解:因为 ,
所以能判断△ABC为直角三角形,
故A不符合题意;
因为 ,
设 ,
则
所以不能判断△ABC为直角三角形,
故B符合题意;
因为 ,
所以
所以能判断△ABC为直角三角形,
故C不符合题意;
因为 ,
所以
所以能判断△ABC为直角三角形,
故D不符合题意;
故答案为:B.
【分析】根据勾股定理的逆定理,一个三角形的三边满足较小两边的平方和等于最大边长的平方,则该三角形就是直角三角形,据此判断A、B、D;根据三角形的内角和定理及有一个角是直角的三角形就是直角三角形可判断C.
9.【答案】C
【解析】【解答】解:,,,
由勾股定理逆定理得:.
由折叠的性质知,,,.
,
在中,由勾股定理得,
即,
解得:.
.
故答案为:C.
【分析】由勾股定理逆定理得∠ACB=90°,由折叠的性质知AE=AC=6,DE=CD,∠AED=∠C=90°,则BE=AB-AE=4,在Rt△BDE中,根据勾股定理可得CD的值,进而可得BD.
10.【答案】A
【解析】【解答】解:如图所示: m, m, m, m,
在 中,
m,
在 中,
m,
∴ m,
故答案为:A.
【分析】先利用勾股定理求出AO和CO的长,再利用线段的和差列出算式求解即可。
11.【答案】20
【解析】【解答】解:在Rt△ABC中,AB=40m,BC=30m,则:AC= =50m
所以少走的路为40+30-50=20m.
故答案为:20 .
【分析】先用勾股定理求出AC的长,然后用AB+BC-AC求出少走的路即可.
12.【答案】25
【解析】【解答】解:如图,过点A作于点D,
∵,,
∴,,,
∴
.
故答案为:25.
【分析】过点A作于点D,利用勾股定理及等量代换可得。
13.【答案】1.5
【解析】【解答】解:如图,
由∠C为直角得到BC=
故答案为:1.5.
【分析】根据勾股定理即可求解.
14.【答案】2.5
【解析】【解答】解:∵公路AC,BC互相垂直,
∴∠ACB=90°,
∵ , ,
在Rt△ABC中,
根据勾股定理AB= km
∵M为AB的中点,
∴CM= km,
即M,C两点间的距离为2.5km,
故答案为:2.5.
【分析】在Rt△ABC中,根据勾股定理求出AB长,再根据三角形斜边中线的性质,即可作答.
15.【答案】解:∵CD是中AB边上的高,
∴△ACD和△BCD都是直角三角形.
在Rt△ACD中
∴,
∵,
∴,
在Rt△BCD中,
.
【解析】【分析】先求出 △ACD和△BCD都是直角三角形,再利用勾股定理求出AD=3,最后利用勾股定理计算求解即可。
16.【答案】解:根据勾股定理得,蔬菜大棚的斜面的宽度即直角三角形的斜边长为:
,
所以蔬菜大棚的斜面面积为:10×20=200.
答:阳光透过的最大面积为200.
【解析】【分析】根据勾股定理得:蔬菜大棚的斜面的宽度即直角三角形的斜边长为10,然后根据矩形的面积公式进行计算.
17.【答案】解:的三条边长分别为,,,,,,
,
是直角三角形.
【解析】【分析】根据已知条件可得a2+b2=(m-n)2+4mn=(m+n)2,c2=(m+n)2,然后结合勾股定理逆定理进行解答.
18.【答案】解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺.
∴EA=EC-AC=5-1=4(尺),
OE=OA-AE=(x-4)尺,
在Rt△OEB中,OE=(x-4)尺,OB=x尺,EB=10尺.
根据勾股定理得:x2=﹙x-4﹚2+102,
整理得:8x=116,
即2x=29,
解得:x=14.5,
答:秋千绳索的长度是l4.5尺.
【解析】【分析】设OA=OB=x尺,根据已知条件,表示出OE,在Rt△OEB中,根据勾股定理列方程,解方程即可.
19.【答案】(1)解:平分,
,
,
,
,
,
,
;
(2)解:平分,,,
,
,
,
,,
,,,
,
设,
,
,
,
解得,
,
的面积为:
.
【解析】【分析】(1)根据角平分线的概念可得∠BAD=∠CAD,由等腰三角形的性质可得∠CAD=∠C,则∠BAD=∠CAD=∠C,∠BAC=2∠C,由∠BAC+∠C=90°可得∠C的度数;
(2)根据角平分线的性质可得DB=DE,利用HL证明△ABD≌△AED,由全等三角形的性质可得AE=AB=3,CE=AC-AE=2,利用勾股定理可求出BC的值,设BD=DE=x,则CD=4-x,然后在Rt△CDE中,根据勾股定理求出x的值,接下来根据三角形的面积公式进行计算.
20.【答案】(1)证明:∵BC=13,CD=12,BD=5,52+122=132,
∴BC2=BD2+CD2,
∴△BDC为直角三角形;
(2)解:设AB=x,
∵△ABC是等腰三角形,
∴AB=AC=x,
∵AC2=AD2+CD2,
即x2=(x﹣5)2+122,
解得:x=16.9,
∴AC=16.9.
【解析】【分析】(1)由BC=13,CD=12,BD=5,得出BC2=BD2+CD2,即可得出△BDC为直角三角形;
(2)由(1)可求出AC的长。
21.【答案】(1)解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
【解析】【分析】(1)先利用勾股定理的逆定理可得△ACB是直角三角形,∠ACB=90°,再结合三角形的面积求出CD的长即可;
(2)先利用勾股定理求出BD的长,再利用线段的和差求解即可。
22.【答案】(1)解:在中,km,km,
(km),
答:监测点与监测点之间的距离为500km;
(2)解:海港受台风影响,
理由:,,
,
,
km,
以台风中心为圆心周围260km以内为受影响区域,
海港会受到此次台风的影响,
以为圆心,260km长为半径画弧,交于,,
则km时,正好影响港口,
在中,
(km),
km,
台风的速度为25千米小时,
(小时).
答:台风影响该海港持续的时间为8小时.
【解析】【分析】(1)利用勾股定理计算即可;
(2) 海港受台风影响,理由:利用三角形的面积公式可求出CE的长,与260km进行比较,可得出 海港受台风影响; 以为圆心,260km长为半径画弧,交于,, 则DE=EF=260km,利用勾股定理求出DE,进而求出DF的长,根据时间=路程÷速度即可求解.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
