第十二章全等三角形单元复习题2023-2024学年人教版八年级数学上册(含解析)
文档属性
| 名称 | 第十二章全等三角形单元复习题2023-2024学年人教版八年级数学上册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册第十二章全等三角形单元复习题
一、选择题
1.如图, ,其中 , ,则 ( )
A.60° B.100° C.120° D.135°
2.全等三角形是( )
A.形状相同的两个三角形 B.周长相等的两个三角形
C.面积相等的两个三角形 D.完全重合的两个三角形
3.如图,已知∠1=∠2,要得到结论ABC≌ADC,不能添加的条件是( )
A.BC=DC B.∠ACB=∠ACD
C.AB=AD D.∠B=∠D
4.下列说法正确的是( )
A.如果两个三角形的周长相等,那么这两个三角形一定全等
B.同位角相等
C.在同一平面内经过直线外一点有且只有一条直线与已知直线平行
D.一个角的补角一定是钝角
5.如图,,,平分,则为( )
A. B. C. D.
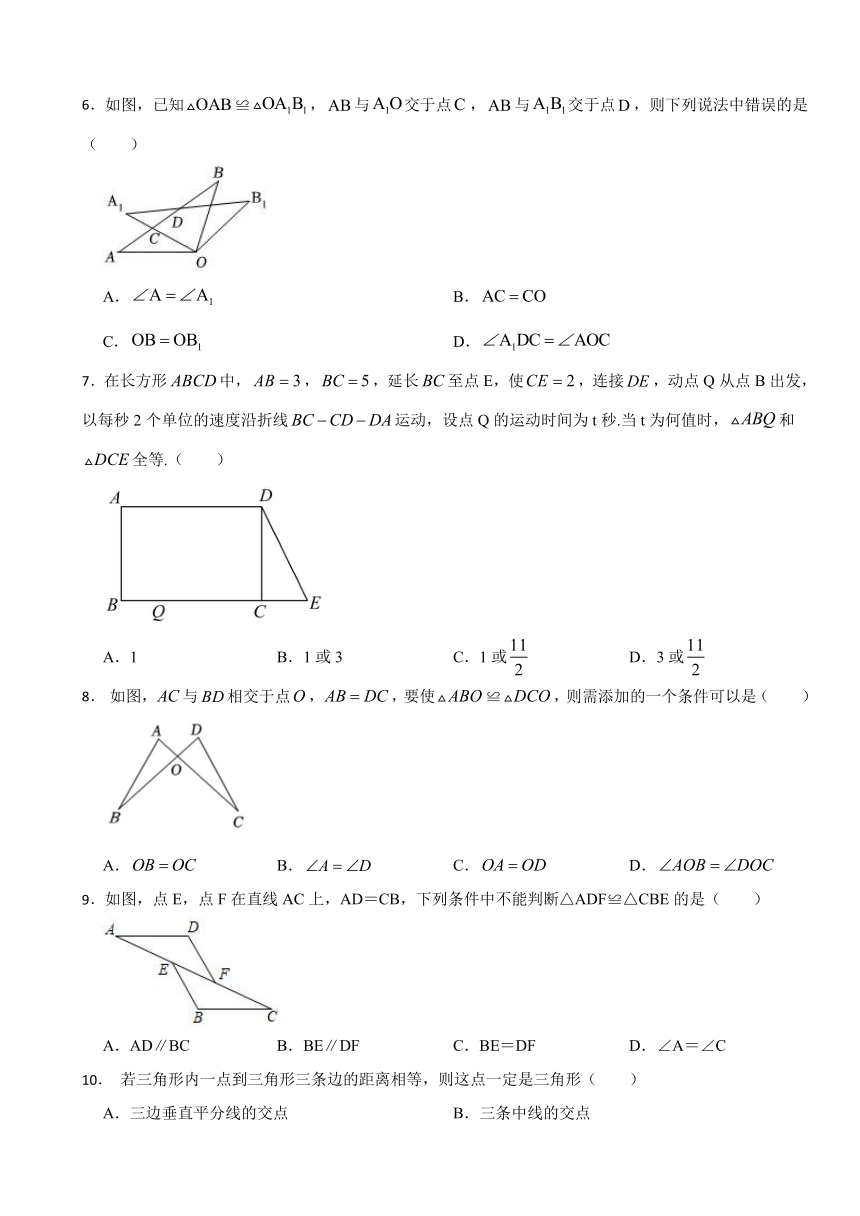
6.如图,已知≌,与交于点,与交于点,则下列说法中错误的是( )
A. B.
C. D.
7.在长方形中,,,延长至点E,使,连接,动点Q从点B出发,以每秒2个单位的速度沿折线运动,设点Q的运动时间为t秒.当t为何值时,和全等.( )
A.1 B.1或3 C.1或 D.3或
8. 如图,与相交于点,,要使≌,则需添加的一个条件可以是( )
A. B. C. D.
9.如图,点E,点F在直线AC上,AD=CB,下列条件中不能判断△ADF≌△CBE的是( )
A.AD∥BC B.BE∥DF C.BE=DF D.∠A=∠C
10. 若三角形内一点到三角形三条边的距离相等,则这点一定是三角形( )
A.三边垂直平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条内角平分线的交点
二、填空题
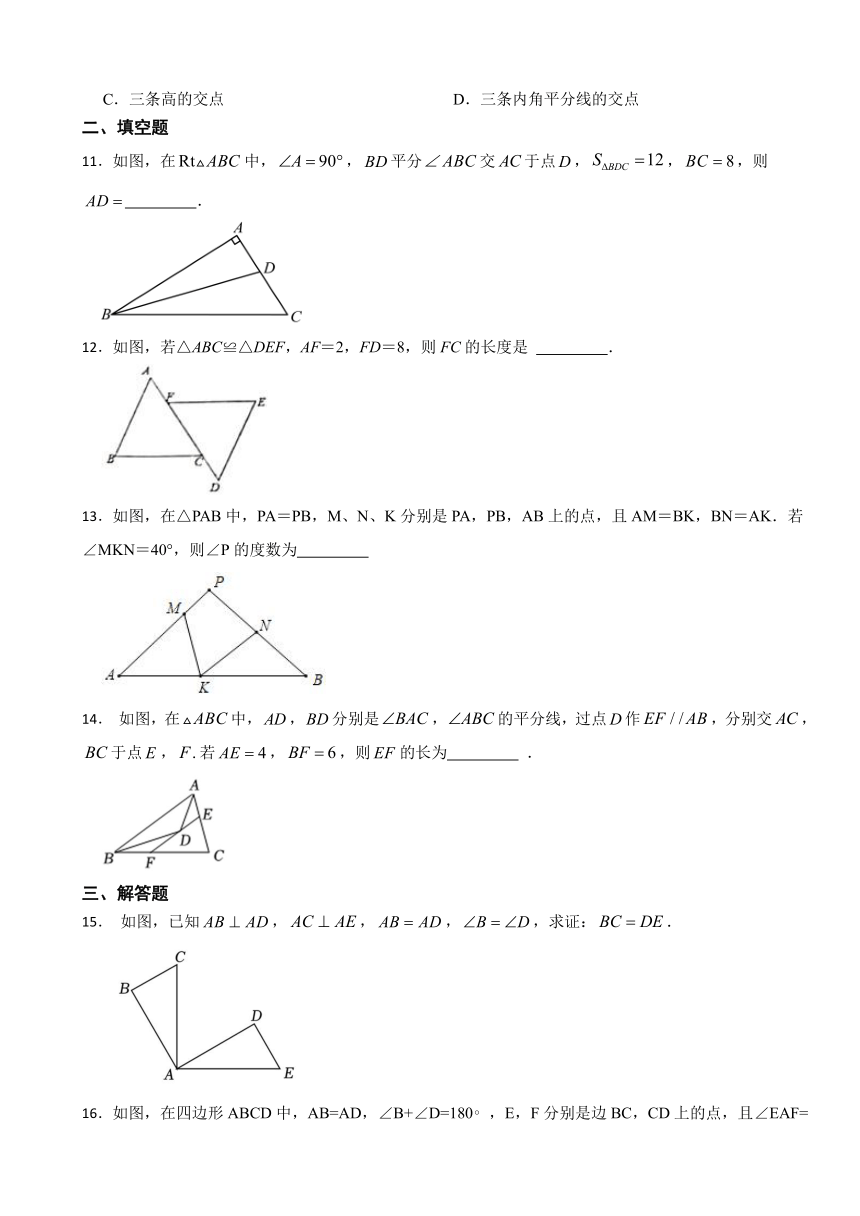
11.如图,在中,,平分交于点,,,则 .
12.如图,若△ABC≌△DEF,AF=2,FD=8,则FC的长度是 .
13.如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
14. 如图,在中,,分别是,的平分线,过点作,分别交,于点,若,,则的长为 .
三、解答题
15. 如图,已知,,,,求证:.
16.如图,在四边形ABCD中,AB=AD,∠B+∠D=180 ,E,F分别是边BC,CD上的点,且∠EAF= ∠BAD,求证:EF=BE+FD.
17.已知:如图,在中,,过点C作,垂足为D.在射线上截取,过点E作,交的延长线于点F.
(1)求证:;
(2)若,,求的长.
18.如图,在中,是的外角的平分线,交的延长线于点E.
(1)若,,则 ;
(2)若,且,求的度数.
四、综合题
19.如图,是等腰直角三角形,.
(1)尺规作图:作的角平分线,交于点D(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,延长至点E,使,连接.求证:,且.
20.已知:如图,,且,,,四点在一条直线上,,,,.
(1)求的度数与的长;
(2)求证:.
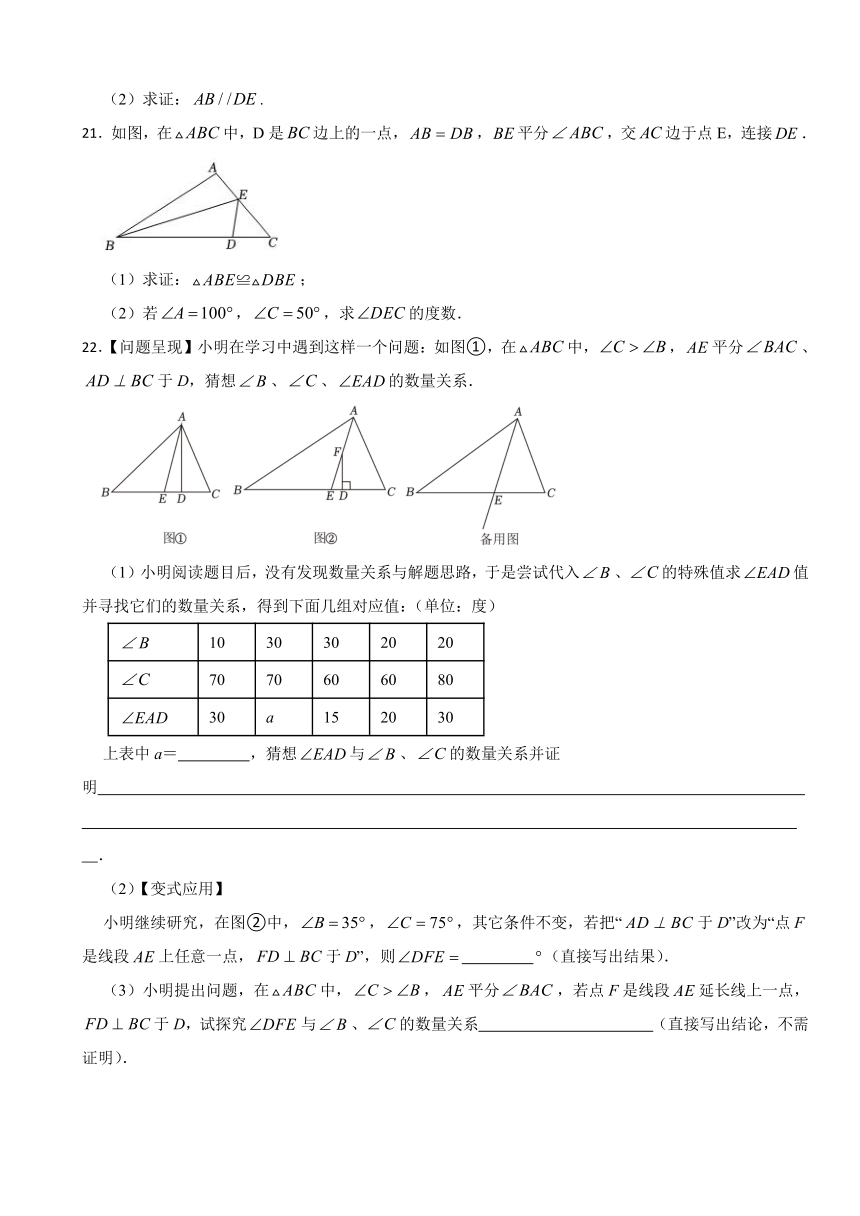
21.如图,在中,D是边上的一点,,平分,交边于点E,连接.
(1)求证:;
(2)若,,求的度数.
22.【问题呈现】小明在学习中遇到这样一个问题:如图①,在中,,平分、于D,猜想、、的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入、的特殊值求值并寻找它们的数量关系,得到下面几组对应值:(单位:度)
10 30 30 20 20
70 70 60 60 80
30 a 15 20 30
上表中a= ,猜想与、的数量关系并证明 .
(2)【变式应用】
小明继续研究,在图②中,,,其它条件不变,若把“于D”改为“点F是线段上任意一点,于D”,则 (直接写出结果).
(3)小明提出问题,在中,,平分,若点F是线段延长线上一点,于D,试探究与、的数量关系 (直接写出结论,不需证明).
答案解析部分
1.【答案】C
【解析】【解答】解:∵ ,
∴ ,
∵ ,
∴ ;
故答案为:C.
【分析】由全等三角形的对应角相等可得∠C=∠C ,再结合已知条件用三角形的内角和定理可求解.
2.【答案】D
【解析】【解答】解:能够完全重合的两个三角形是全等三角形,故D正确,A、B、C错误。
故答案为:D.
【分析】根据全等三角形的定义判定即可。
3.【答案】A
【解析】【解答】由题意可知,∠1=∠2,AC=AC.
A:BC=DC,添加后,不能证明 ,符合题意;
B:∠ACB=∠ACD,结合题干,通过ASA证明,不合题意;
C:AB=AD,结合题干,通过SAS证明,不合题意;
D:∠B=∠D,结合题干,通过AAS证明,不合题意;
故答案为:A.
【分析】本题考查三角形的全等判定。熟悉三角形全等判定的方法(边边边,边角边,角边角,角角边,斜边直角边(直角三角形))是解题的关键。
4.【答案】C
【解析】【解答】解:A、如果两个三角形的周长相等,那么这两个三角形不一定全等,故选项A不符合题意;
B、两直线平行,同位角相等,故选项B不符合题意;
C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行,故选项C符合题意;
D、一个角的补角不一定是钝角,故选项D不符合题意.
故答案为:C.
【分析】根据全等三角形的判定定理:两角及其一角的对边对应相等的三角形全等;斜边及一条直角边对应相等的两个直角三角形全等;两边和它们的夹角对应相等的两个三角形全等;两个角和它们所夹的边分别对应相等的两个三角形全等;两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补;经过直线外一点,有且只有一条直线与已知直线平行;若两角之和满足180°,那么这两个角互为补角.其中一个角叫做另一个角的补角,据此逐项分析即可得出答案.
5.【答案】C
【解析】【解答】解:,
,
平分 ,
,
,
.
故答案为:C.
【分析】根据 ,,以及平行线的性质,得到,又由 平分 得到 ,即可求出答.
6.【答案】B
【解析】【解答】解:∵≌,
∴ , ,
又∵∠ACD=∠ACO,
∴ ,
∴A、C、D正确.
故答案为:B.
【分析】根据全等三角形的性质、8字模型可得.
7.【答案】C
【解析】【解答】解:∵,
∴或,
当时,,
此时,
解得,
当时,,
此时,即,
解得.
∴当或时,和全等.
故答案为:C.
【分析】当△ABQ≌△DCE时,BQ=CE=2,此时2t=2,求解可得t的值;当△BAQ≌△DCE时,AQ=CE=2,此时BC+CD+DQ=BC+CD+(DA-AQ)=11,此时2t=11,求解可得t的值.
8.【答案】B
9.【答案】B
【解析】【解答】解:∵AE=CF,∴AF=CE,
A、添加AD//BC,可得到∠A=∠C,由“SAS”可以判定△ADF≌△CBE,∴A选项正确,不符合题意;
B、添加BE//DF,可得到∠BEC=∠ AFD,不能判定△ADF≌△CBE,∴B选项不正确,符合题意;
C、添加BE=DF,由“SSS”可以判定△ADF≌△CBE,∴C选项正确,不符合题意;
D、添加∠A=∠C,由“SAS”可以判定△ADF≌△CBE,∴D选项正确,不符合题意;
故答案为:B.
【分析】利用全等三角形的判定方法逐项判断即可.
10.【答案】D
11.【答案】3
【解析】【解答】解:作DE垂直BC于点E
, 平分
即AD=3
故答案为3
【分析】作三角形BDC以BC为底的高,利用面积求高DE,利用角平分线可证明AD=DE即可求出答案。
12.【答案】6
【解析】【解答】解:∵△ABC≌△DEF,
∴AC=DF=8
∴FC=AC-AF=8-2=6.
故答案为:6.
【分析】利用全等三角形的性质可求出AC的长,再根据FC=AC-AF,代入计算求出FC的长.
13.【答案】100°
【解析】【解答】解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN,
∵∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=40°,
∴∠P=180°﹣∠A﹣∠B=180°﹣40°﹣40°=100°,
故答案为100°
【分析】先证明△AMK≌△BKN(SAS),再结合外角的性质可求得∠A=∠MKN,在利用三角形内角和定理即可求得角P的度数。
14.【答案】10
【解析】【解答】解:由题意可得:
故答案为:10
【分析】根据角平分线性质进行角之间的等量替换,平行线的性质即可求出答案。
15.【答案】证明:
在
16.【答案】证明:如图将△ADF顺时针旋转得到△ABG,使得AD与AB重合,
则△ADF≌△ABG,
∴∠FAG=∠BAD,AF=AG,DF=GB,
∵ ,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=EF,
∵GE=GB+BE=DF+BE,
∴EF=BE+FD.
【解析】【分析】根据旋转前后图形全等可得△ADF≌△ABG,即可得到对应角相等,结合已知∠EAF=∠BAD即可推出∠EAF=∠EAG,则不难证明△EAG≌△EAF,根据全等三角形的性质得GE=EF,则不难证明结论.
17.【答案】(1)证明:∵,,
∴,
∴,
在和中,
,
∴
(2)解:∵,
∴,,
∴
18.【答案】(1)
(2)解:∵平分,
∴,
∵,,
∴,
即,
∴,
∴.
19.【答案】(1)解:如图,即为所作,
(2)解:如图,延长,交于,
∵是等腰直角三角形,
∴
又∵
∴
∴,,
∴,
∴,即.
【解析】【分析】(1)利用基本尺规作图作角平分线即可;
(2)证明解题即可.
20.【答案】(1)解:∵,,
∴.
∵,
∴,
,
∵,,
∴.
(2)证明:∵,
∴,
∴.
【解析】【分析】(1)首先由内角和定理可得∠ACB=35°,由全等三角形的性质可得DE=AB,∠F=∠ACB=35°,然后根据DH=DE-HE=AB-HE进行计算;
(2)由全等三角形的性质可得∠B=∠DEF,然后利用平行线的判定定理进行证明.
21.【答案】(1)证明:∵平分,
∴,
在和中,
∵,
∴;
(2)解:∵,
∴,
∵,
∴.
【解析】【分析】(1)利用“SAS”证明即可;
(2)根据全等三角形的性质可得,再结合,可得。
22.【答案】(1)20;解:,,, , .
(2)20
(3)
【解析】【解答】解:(1) , ,
,
中, ,
平分 ,
,
,
;
(2)过点A作 于G,如图所示:
, ,
,
,
, ,
由(1)同理可得: ,
,
故答案为:20.
(3)过A作 于G,而 ,如图所示:
,
,
由(1)同理可得: ,
,
故答案为:
【分析】(1)先根据三角形内角和定理即可得到 ,再结合题意运用角平分线的性质即可求解;
(2)过点A作 于G,先根据平行线的判定与性质即可得到 ,由(1)同理可得: ,进而即可求解;
(3)过A作 于G,而 ,先根据平行线的性质即可得到 ,由(1)同理可得: ,进而即可求解。
一、选择题
1.如图, ,其中 , ,则 ( )
A.60° B.100° C.120° D.135°
2.全等三角形是( )
A.形状相同的两个三角形 B.周长相等的两个三角形
C.面积相等的两个三角形 D.完全重合的两个三角形
3.如图,已知∠1=∠2,要得到结论ABC≌ADC,不能添加的条件是( )
A.BC=DC B.∠ACB=∠ACD
C.AB=AD D.∠B=∠D
4.下列说法正确的是( )
A.如果两个三角形的周长相等,那么这两个三角形一定全等
B.同位角相等
C.在同一平面内经过直线外一点有且只有一条直线与已知直线平行
D.一个角的补角一定是钝角
5.如图,,,平分,则为( )
A. B. C. D.
6.如图,已知≌,与交于点,与交于点,则下列说法中错误的是( )
A. B.
C. D.
7.在长方形中,,,延长至点E,使,连接,动点Q从点B出发,以每秒2个单位的速度沿折线运动,设点Q的运动时间为t秒.当t为何值时,和全等.( )
A.1 B.1或3 C.1或 D.3或
8. 如图,与相交于点,,要使≌,则需添加的一个条件可以是( )
A. B. C. D.
9.如图,点E,点F在直线AC上,AD=CB,下列条件中不能判断△ADF≌△CBE的是( )
A.AD∥BC B.BE∥DF C.BE=DF D.∠A=∠C
10. 若三角形内一点到三角形三条边的距离相等,则这点一定是三角形( )
A.三边垂直平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条内角平分线的交点
二、填空题
11.如图,在中,,平分交于点,,,则 .
12.如图,若△ABC≌△DEF,AF=2,FD=8,则FC的长度是 .
13.如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
14. 如图,在中,,分别是,的平分线,过点作,分别交,于点,若,,则的长为 .
三、解答题
15. 如图,已知,,,,求证:.
16.如图,在四边形ABCD中,AB=AD,∠B+∠D=180 ,E,F分别是边BC,CD上的点,且∠EAF= ∠BAD,求证:EF=BE+FD.
17.已知:如图,在中,,过点C作,垂足为D.在射线上截取,过点E作,交的延长线于点F.
(1)求证:;
(2)若,,求的长.
18.如图,在中,是的外角的平分线,交的延长线于点E.
(1)若,,则 ;
(2)若,且,求的度数.
四、综合题
19.如图,是等腰直角三角形,.
(1)尺规作图:作的角平分线,交于点D(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,延长至点E,使,连接.求证:,且.
20.已知:如图,,且,,,四点在一条直线上,,,,.
(1)求的度数与的长;
(2)求证:.
21.如图,在中,D是边上的一点,,平分,交边于点E,连接.
(1)求证:;
(2)若,,求的度数.
22.【问题呈现】小明在学习中遇到这样一个问题:如图①,在中,,平分、于D,猜想、、的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入、的特殊值求值并寻找它们的数量关系,得到下面几组对应值:(单位:度)
10 30 30 20 20
70 70 60 60 80
30 a 15 20 30
上表中a= ,猜想与、的数量关系并证明 .
(2)【变式应用】
小明继续研究,在图②中,,,其它条件不变,若把“于D”改为“点F是线段上任意一点,于D”,则 (直接写出结果).
(3)小明提出问题,在中,,平分,若点F是线段延长线上一点,于D,试探究与、的数量关系 (直接写出结论,不需证明).
答案解析部分
1.【答案】C
【解析】【解答】解:∵ ,
∴ ,
∵ ,
∴ ;
故答案为:C.
【分析】由全等三角形的对应角相等可得∠C=∠C ,再结合已知条件用三角形的内角和定理可求解.
2.【答案】D
【解析】【解答】解:能够完全重合的两个三角形是全等三角形,故D正确,A、B、C错误。
故答案为:D.
【分析】根据全等三角形的定义判定即可。
3.【答案】A
【解析】【解答】由题意可知,∠1=∠2,AC=AC.
A:BC=DC,添加后,不能证明 ,符合题意;
B:∠ACB=∠ACD,结合题干,通过ASA证明,不合题意;
C:AB=AD,结合题干,通过SAS证明,不合题意;
D:∠B=∠D,结合题干,通过AAS证明,不合题意;
故答案为:A.
【分析】本题考查三角形的全等判定。熟悉三角形全等判定的方法(边边边,边角边,角边角,角角边,斜边直角边(直角三角形))是解题的关键。
4.【答案】C
【解析】【解答】解:A、如果两个三角形的周长相等,那么这两个三角形不一定全等,故选项A不符合题意;
B、两直线平行,同位角相等,故选项B不符合题意;
C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行,故选项C符合题意;
D、一个角的补角不一定是钝角,故选项D不符合题意.
故答案为:C.
【分析】根据全等三角形的判定定理:两角及其一角的对边对应相等的三角形全等;斜边及一条直角边对应相等的两个直角三角形全等;两边和它们的夹角对应相等的两个三角形全等;两个角和它们所夹的边分别对应相等的两个三角形全等;两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补;经过直线外一点,有且只有一条直线与已知直线平行;若两角之和满足180°,那么这两个角互为补角.其中一个角叫做另一个角的补角,据此逐项分析即可得出答案.
5.【答案】C
【解析】【解答】解:,
,
平分 ,
,
,
.
故答案为:C.
【分析】根据 ,,以及平行线的性质,得到,又由 平分 得到 ,即可求出答.
6.【答案】B
【解析】【解答】解:∵≌,
∴ , ,
又∵∠ACD=∠ACO,
∴ ,
∴A、C、D正确.
故答案为:B.
【分析】根据全等三角形的性质、8字模型可得.
7.【答案】C
【解析】【解答】解:∵,
∴或,
当时,,
此时,
解得,
当时,,
此时,即,
解得.
∴当或时,和全等.
故答案为:C.
【分析】当△ABQ≌△DCE时,BQ=CE=2,此时2t=2,求解可得t的值;当△BAQ≌△DCE时,AQ=CE=2,此时BC+CD+DQ=BC+CD+(DA-AQ)=11,此时2t=11,求解可得t的值.
8.【答案】B
9.【答案】B
【解析】【解答】解:∵AE=CF,∴AF=CE,
A、添加AD//BC,可得到∠A=∠C,由“SAS”可以判定△ADF≌△CBE,∴A选项正确,不符合题意;
B、添加BE//DF,可得到∠BEC=∠ AFD,不能判定△ADF≌△CBE,∴B选项不正确,符合题意;
C、添加BE=DF,由“SSS”可以判定△ADF≌△CBE,∴C选项正确,不符合题意;
D、添加∠A=∠C,由“SAS”可以判定△ADF≌△CBE,∴D选项正确,不符合题意;
故答案为:B.
【分析】利用全等三角形的判定方法逐项判断即可.
10.【答案】D
11.【答案】3
【解析】【解答】解:作DE垂直BC于点E
, 平分
即AD=3
故答案为3
【分析】作三角形BDC以BC为底的高,利用面积求高DE,利用角平分线可证明AD=DE即可求出答案。
12.【答案】6
【解析】【解答】解:∵△ABC≌△DEF,
∴AC=DF=8
∴FC=AC-AF=8-2=6.
故答案为:6.
【分析】利用全等三角形的性质可求出AC的长,再根据FC=AC-AF,代入计算求出FC的长.
13.【答案】100°
【解析】【解答】解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN,
∵∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=40°,
∴∠P=180°﹣∠A﹣∠B=180°﹣40°﹣40°=100°,
故答案为100°
【分析】先证明△AMK≌△BKN(SAS),再结合外角的性质可求得∠A=∠MKN,在利用三角形内角和定理即可求得角P的度数。
14.【答案】10
【解析】【解答】解:由题意可得:
故答案为:10
【分析】根据角平分线性质进行角之间的等量替换,平行线的性质即可求出答案。
15.【答案】证明:
在
16.【答案】证明:如图将△ADF顺时针旋转得到△ABG,使得AD与AB重合,
则△ADF≌△ABG,
∴∠FAG=∠BAD,AF=AG,DF=GB,
∵ ,
∴∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS),
∴GE=EF,
∵GE=GB+BE=DF+BE,
∴EF=BE+FD.
【解析】【分析】根据旋转前后图形全等可得△ADF≌△ABG,即可得到对应角相等,结合已知∠EAF=∠BAD即可推出∠EAF=∠EAG,则不难证明△EAG≌△EAF,根据全等三角形的性质得GE=EF,则不难证明结论.
17.【答案】(1)证明:∵,,
∴,
∴,
在和中,
,
∴
(2)解:∵,
∴,,
∴
18.【答案】(1)
(2)解:∵平分,
∴,
∵,,
∴,
即,
∴,
∴.
19.【答案】(1)解:如图,即为所作,
(2)解:如图,延长,交于,
∵是等腰直角三角形,
∴
又∵
∴
∴,,
∴,
∴,即.
【解析】【分析】(1)利用基本尺规作图作角平分线即可;
(2)证明解题即可.
20.【答案】(1)解:∵,,
∴.
∵,
∴,
,
∵,,
∴.
(2)证明:∵,
∴,
∴.
【解析】【分析】(1)首先由内角和定理可得∠ACB=35°,由全等三角形的性质可得DE=AB,∠F=∠ACB=35°,然后根据DH=DE-HE=AB-HE进行计算;
(2)由全等三角形的性质可得∠B=∠DEF,然后利用平行线的判定定理进行证明.
21.【答案】(1)证明:∵平分,
∴,
在和中,
∵,
∴;
(2)解:∵,
∴,
∵,
∴.
【解析】【分析】(1)利用“SAS”证明即可;
(2)根据全等三角形的性质可得,再结合,可得。
22.【答案】(1)20;解:,,, , .
(2)20
(3)
【解析】【解答】解:(1) , ,
,
中, ,
平分 ,
,
,
;
(2)过点A作 于G,如图所示:
, ,
,
,
, ,
由(1)同理可得: ,
,
故答案为:20.
(3)过A作 于G,而 ,如图所示:
,
,
由(1)同理可得: ,
,
故答案为:
【分析】(1)先根据三角形内角和定理即可得到 ,再结合题意运用角平分线的性质即可求解;
(2)过点A作 于G,先根据平行线的判定与性质即可得到 ,由(1)同理可得: ,进而即可求解;
(3)过A作 于G,而 ,先根据平行线的性质即可得到 ,由(1)同理可得: ,进而即可求解。
