3.2勾股定理的逆定理 同步提优练习 (无答案)2023-2024学年苏科版数学八年级上册
文档属性
| 名称 | 3.2勾股定理的逆定理 同步提优练习 (无答案)2023-2024学年苏科版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
3.2勾股定理的逆定理(同步提优练习)
选择题(本题共10小题)
1.下列各组数中,能构成直角三角形的为( )
A.1,1,2 B.15,21,25 C.7,24,25 D.6,12,13
2.已知三角形的三边长为6、8、10,则这个三角形最长边上的高为( )
A.2.4 B.4.8 C.9.6 D.10
3.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了( ),却踩坏了花草.
A.1米 B.2米 C.3米 D.4米
4.如图,由小正方形组成的网格图,每个小正方形的边长均为1,图中标有线段,,,,其中能构成一个直角三角形三边的是( )
,, B.,,
C.,, D.,,
5.如图,在 4×4 的正方形网格中(每个小正方形边长均为 1),点A,B,C 在格点上,连接 AB,AC,BC,则△ABC 的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
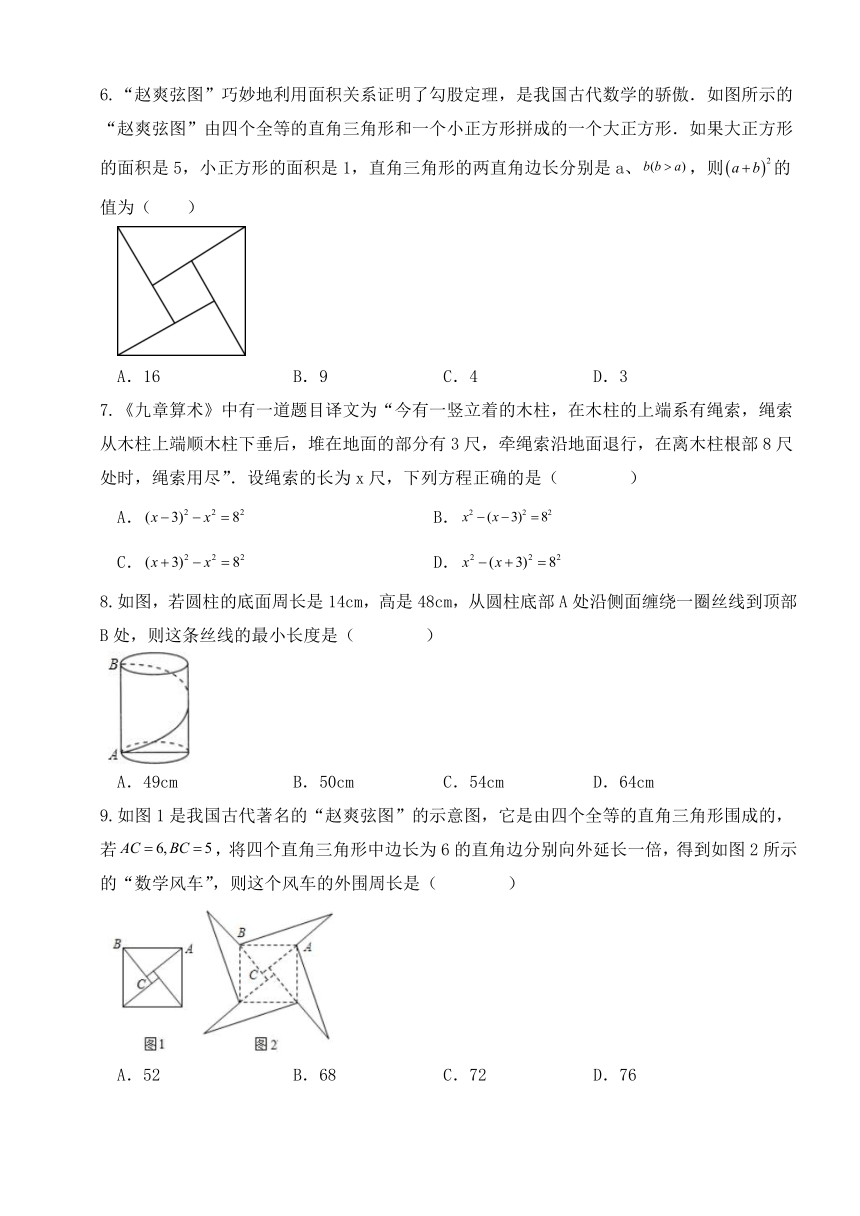
6.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果大正方形的面积是5,小正方形的面积是1,直角三角形的两直角边长分别是a、,则的值为( )
A.16 B.9 C.4 D.3
7.《九章算术》中有一道题目译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分有3尺,牵绳索沿地面退行,在离木柱根部8尺处时,绳索用尽”.设绳索的长为x尺,下列方程正确的是( )
A. B.
C. D.
8.如图,若圆柱的底面周长是14cm,高是48cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.49cm B.50cm C.54cm D.64cm
9.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
A.52 B.68 C.72 D.76
10.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘B处离桌面的高度为,此时底部边缘A处与C处间的距离为,小组成员调整张角的大小继续探究,最后发现当张角为时(D是B的对应点),顶部边缘D处到桌面的距离为,则底部边缘A处与E之间的距离为( )
A. B. C. D.
填空题(本题共10小题)
11.有一组勾股数,知道其中的两个数分别是17和8,则第三个数是______.
12.如图,则阴影小长方形的面积S=_____.
13.在△中,已知,,边上的中线,过点作⊥,垂足为点,则的长度是__________.
14.如图所示的网格是正方形网格,A,B,C是网格线交点,则∠ABC+∠BAC= °.
15.若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a+2为边的三角形的面积为______.
16.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门(和),门边沿D,C两点到门槛的距高是1尺(1尺=10寸),两扇门的间隙为2寸,则门槛为_______寸.
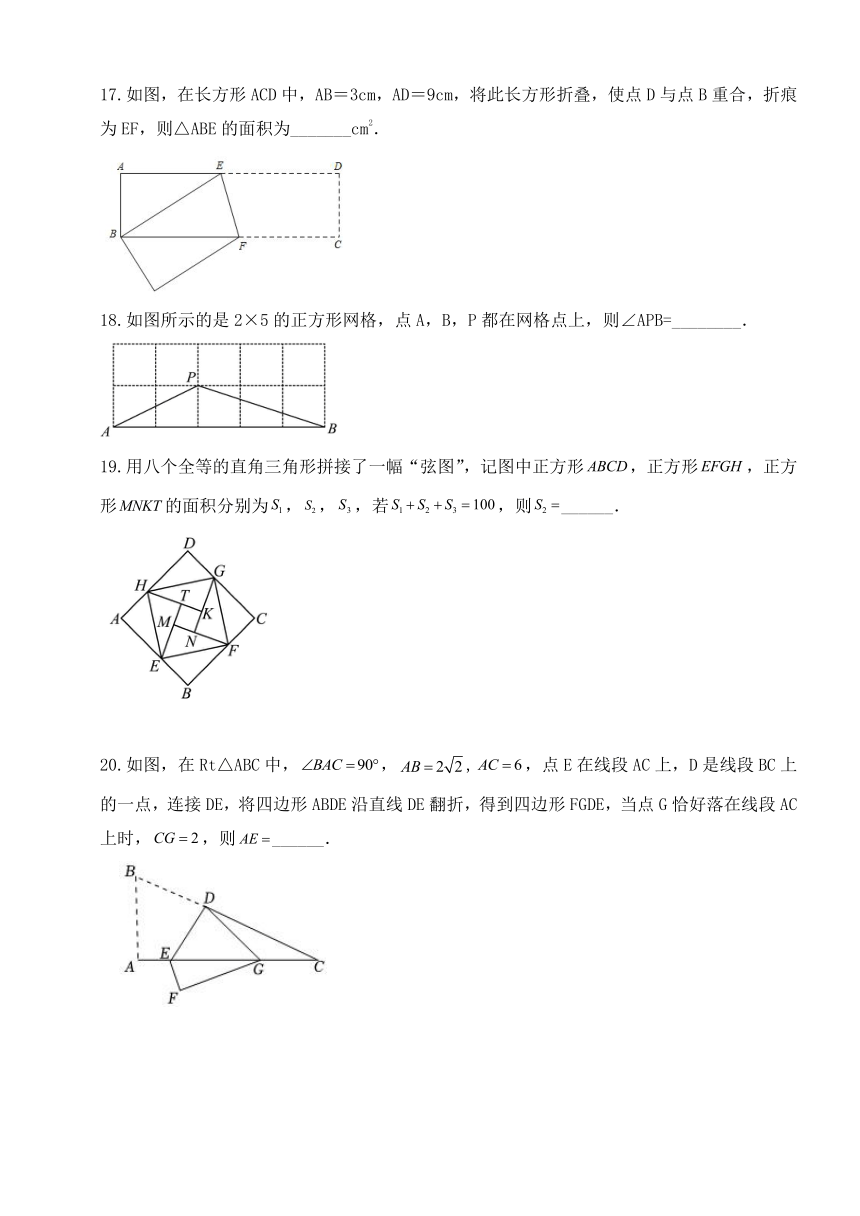
17.如图,在长方形ACD中,AB=3cm,AD=9cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为_______cm2.
18.如图所示的是2×5的正方形网格,点A,B,P都在网格点上,则∠APB=________.
19.用八个全等的直角三角形拼接了一幅“弦图”,记图中正方形,正方形,正方形的面积分别为,,,若,则______.
20.如图,在Rt△ABC中,,,,点E在线段AC上,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,,则______.
解答题(本题共7小题)
21.计算:
(1)在Rt△ABC中,∠C=90°,a=8,b=15,求c
(2)在Rt△ABC中,∠C=90°,a=3,b=4,求c
(3)一个直角三角形的两边长分别为3cm和5cm,求这个三角形的第三边长.
22.如图,在四边形中,,,,,.
求四边形的面积.
23.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=_______,b= _______,c=_______;
(2)猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.
24.如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于Q、R处,且相距30海里.如果知道“远航”号沿北偏东50°方向航行,则“海天”号沿哪个方向航行?
25.勾股定理是一个基本的几何定理,早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”;这三个整数叫做一组“勾股数”.在一次“构造勾股数”的探究性学习中,老师给出了下表:
2 3 3 4
1 1 2 3
4 6 12 24
其中、为正整数,且.
(1)观察表格,当,时,此时对应的、、的值能否为直角三角形三边的长?说明你的理由.
(2)探究,,与、之间的关系并用含、的代数式表示: , , .
(3)以,,为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
26.如图1,Rt△ABC中,∠ABC=90°,BC<AB<2BC.在AB边上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)证明:∠AFM=45°;
(2)若将题中的条件“BC<AB<2BC”改为“AB>2BC”,其他条件不变,请你在图2的位置上画出图形,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,请猜想∠AFM的度数,并说明理由.
27.先阅读下面的材料,再解决问题.
【实际问题】如图1,一圆柱的底面半径为5cm,是底面直径,高为5cm,求一只蚂蚁从点出发沿圆柱表面爬行到点的最短路线,小明设计了两条路线.
【解决方案】路线 1:侧面展开图中的线段,如图所示
设路线1的长度为,则.
路线2:高线底面直径.
设路线2的长度为,则.
为比较,的大小,采用“作差法”:
因为;
所以,所以,
所以小明认为路线2较短.
(1)【问题类比】小亮对 上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高为5 cm".请你用上述方法帮小亮比较出与的大小.
(2)【问题拓展】请你帮他们继续研究:在一般情况下,若圆柱的底面半径为cm,高为cm,蚂蚁从点出发沿圆柱表面爬行到点,当满足什么条件时,路线2较短 请说明理由.
(3)【问题解决】如图是紧密排列在一起的2个相同的圆柱,高为5cm.当蚂蚁从点出发沿圆柱表面爬行到点的两条路线长度相等时,求圆柱的底面半径.
选择题(本题共10小题)
1.下列各组数中,能构成直角三角形的为( )
A.1,1,2 B.15,21,25 C.7,24,25 D.6,12,13
2.已知三角形的三边长为6、8、10,则这个三角形最长边上的高为( )
A.2.4 B.4.8 C.9.6 D.10
3.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了( ),却踩坏了花草.
A.1米 B.2米 C.3米 D.4米
4.如图,由小正方形组成的网格图,每个小正方形的边长均为1,图中标有线段,,,,其中能构成一个直角三角形三边的是( )
,, B.,,
C.,, D.,,
5.如图,在 4×4 的正方形网格中(每个小正方形边长均为 1),点A,B,C 在格点上,连接 AB,AC,BC,则△ABC 的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
6.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果大正方形的面积是5,小正方形的面积是1,直角三角形的两直角边长分别是a、,则的值为( )
A.16 B.9 C.4 D.3
7.《九章算术》中有一道题目译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分有3尺,牵绳索沿地面退行,在离木柱根部8尺处时,绳索用尽”.设绳索的长为x尺,下列方程正确的是( )
A. B.
C. D.
8.如图,若圆柱的底面周长是14cm,高是48cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.49cm B.50cm C.54cm D.64cm
9.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
A.52 B.68 C.72 D.76
10.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘B处离桌面的高度为,此时底部边缘A处与C处间的距离为,小组成员调整张角的大小继续探究,最后发现当张角为时(D是B的对应点),顶部边缘D处到桌面的距离为,则底部边缘A处与E之间的距离为( )
A. B. C. D.
填空题(本题共10小题)
11.有一组勾股数,知道其中的两个数分别是17和8,则第三个数是______.
12.如图,则阴影小长方形的面积S=_____.
13.在△中,已知,,边上的中线,过点作⊥,垂足为点,则的长度是__________.
14.如图所示的网格是正方形网格,A,B,C是网格线交点,则∠ABC+∠BAC= °.
15.若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a+2为边的三角形的面积为______.
16.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门(和),门边沿D,C两点到门槛的距高是1尺(1尺=10寸),两扇门的间隙为2寸,则门槛为_______寸.
17.如图,在长方形ACD中,AB=3cm,AD=9cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为_______cm2.
18.如图所示的是2×5的正方形网格,点A,B,P都在网格点上,则∠APB=________.
19.用八个全等的直角三角形拼接了一幅“弦图”,记图中正方形,正方形,正方形的面积分别为,,,若,则______.
20.如图,在Rt△ABC中,,,,点E在线段AC上,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,,则______.
解答题(本题共7小题)
21.计算:
(1)在Rt△ABC中,∠C=90°,a=8,b=15,求c
(2)在Rt△ABC中,∠C=90°,a=3,b=4,求c
(3)一个直角三角形的两边长分别为3cm和5cm,求这个三角形的第三边长.
22.如图,在四边形中,,,,,.
求四边形的面积.
23.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=_______,b= _______,c=_______;
(2)猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.
24.如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于Q、R处,且相距30海里.如果知道“远航”号沿北偏东50°方向航行,则“海天”号沿哪个方向航行?
25.勾股定理是一个基本的几何定理,早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”;这三个整数叫做一组“勾股数”.在一次“构造勾股数”的探究性学习中,老师给出了下表:
2 3 3 4
1 1 2 3
4 6 12 24
其中、为正整数,且.
(1)观察表格,当,时,此时对应的、、的值能否为直角三角形三边的长?说明你的理由.
(2)探究,,与、之间的关系并用含、的代数式表示: , , .
(3)以,,为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
26.如图1,Rt△ABC中,∠ABC=90°,BC<AB<2BC.在AB边上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)证明:∠AFM=45°;
(2)若将题中的条件“BC<AB<2BC”改为“AB>2BC”,其他条件不变,请你在图2的位置上画出图形,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,请猜想∠AFM的度数,并说明理由.
27.先阅读下面的材料,再解决问题.
【实际问题】如图1,一圆柱的底面半径为5cm,是底面直径,高为5cm,求一只蚂蚁从点出发沿圆柱表面爬行到点的最短路线,小明设计了两条路线.
【解决方案】路线 1:侧面展开图中的线段,如图所示
设路线1的长度为,则.
路线2:高线底面直径.
设路线2的长度为,则.
为比较,的大小,采用“作差法”:
因为;
所以,所以,
所以小明认为路线2较短.
(1)【问题类比】小亮对 上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高为5 cm".请你用上述方法帮小亮比较出与的大小.
(2)【问题拓展】请你帮他们继续研究:在一般情况下,若圆柱的底面半径为cm,高为cm,蚂蚁从点出发沿圆柱表面爬行到点,当满足什么条件时,路线2较短 请说明理由.
(3)【问题解决】如图是紧密排列在一起的2个相同的圆柱,高为5cm.当蚂蚁从点出发沿圆柱表面爬行到点的两条路线长度相等时,求圆柱的底面半径.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
