2020-2021学年山东省聊城市冠县五年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2020-2021学年山东省聊城市冠县五年级(下)期末数学试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 860.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览




文档简介
2020-2021学年山东省聊城市冠县五年级(下)期末数学试卷
一、计算题。(19分)
1.(4分)直接写出得数。
= = = =
= = = =
2.(9分)脱式计算。(能简算的要简算)
3.(6分)解方程。
x+
二、填空题。(27分)
4.(2分)一堆煤3吨,8天烧完,平均每天烧这堆煤的吨.
5.(4分)= (填小数)
6.(2分)具有 的量,可以用正、负数表示。如果+100表示小明向南走了100米,那么小华向北走了150米 米。
7.(2分)5个是 ,是 个。
8.(4分)
48秒= 分 46cm2= dm2 3.08m3= m3 dm3
9.(4分)在横线里填上“>”“<”或“=”。
0.375
10.(2分)18和54的最大公因数是 ,最小公倍数是 。
11.(1分)一个正方体的棱长是3分米,把它切成两个体积相等的长方体,表面积增加了 平方分米。
12.(1分)实验小学从5名候选人中选2人参加象棋比赛,有 种不同的选法。
13.(3分)将两个棱长3厘米的正方体拼成一个长方体。拼成的长方体的棱长总和是 厘米,体积是 立方厘米,表面积是 平方厘米。
14.(2分)一块长方形的布长24分米,宽18分米,要把它裁成正方形手绢(没有剩余) 分米,能裁 块。
三、判断题。(对的画“√”,错的画“×”)(6分)
15.(1分)和大小相等,意义也相同。( .)
16.(1分)在同一数轴上,5和﹣5离0的距离一样长。( .)
17.(1分)如果是假分数,那么b一定大于a.( .)
18.(1分)约分和通分的依据都是分数的基本性质( .)
19.(1分)18只有2、3、6、9这4个因数。( .)
20.(1分)复式条形统计图的优点是不仅可以清楚的表示数量的多少,而且便于对两组数据进行比较.( .)
四、选择题。(将正确答案的序号填在括号里)(10分)
21.(2分)本学期,我们学习异分母分数的加减时,用到的方法是 ;我们学习体积单位时,用到的方法是 。
A.转化
B.数形结合
C.类推
22.(2分)用一根68厘米的铁丝正好弯成一个长方体框架,那么这个长方体一组长、宽、高的和是( )厘米。
A.34 B.18 C.17
23.(2分)分数的分子加上24,要使分数的大小不变( )
A.18 B.27 C.36
24.(2分)下面图形不是正方体展开图的是( )
A. B. C.
25.(2分)一个长8分米、宽3分米、高2.5分米的长方体盒子,最多能放( )棱长是1分米的小正方体木块.
A.48 B.52 C.60
五、实践操作。(14分)
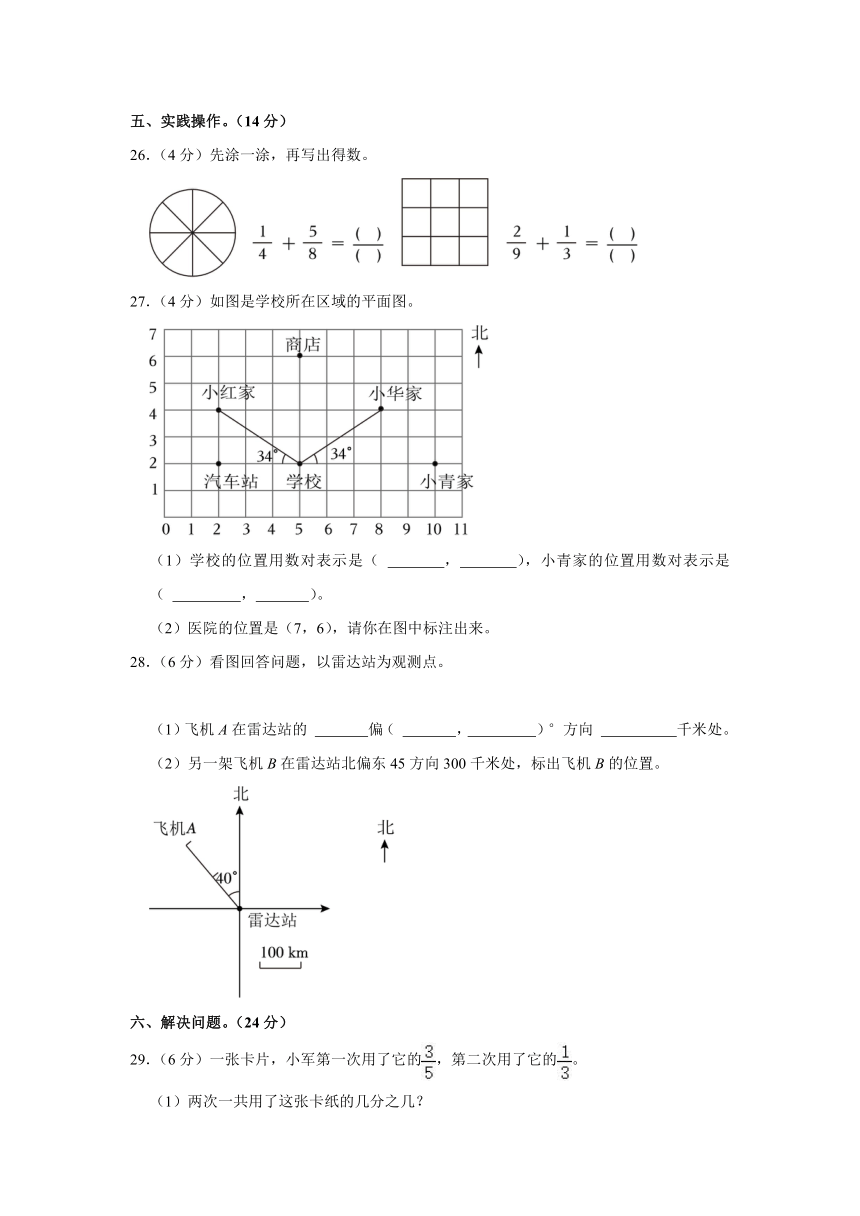
26.(4分)先涂一涂,再写出得数。
27.(4分)如图是学校所在区域的平面图。
(1)学校的位置用数对表示是( , ),小青家的位置用数对表示是( , )。
(2)医院的位置是(7,6),请你在图中标注出来。
28.(6分)看图回答问题,以雷达站为观测点。
(1)飞机A在雷达站的 偏( , )°方向 千米处。
(2)另一架飞机B在雷达站北偏东45方向300千米处,标出飞机B的位置。
六、解决问题。(24分)
29.(6分)一张卡片,小军第一次用了它的,第二次用了它的。
(1)两次一共用了这张卡纸的几分之几?
(2)还剩几分之几?
30.(8分)某游泳池长是60米,宽是40米,深是2.5米。
(1)建造这个游泳池要挖出土多少立方米?
(2)在游泳池的四周都抹上水泥,抹水泥的面积是多少平方米?
(3)如果给这个游泳池注2米深的水,已知每小时能注水75立方米,需用几小时?
31.(10分)如图是2020年北京市和东莞市四个季度的平均气温统计表。
北京市和东莞市四个季度平均气温统计表
第一季度 第二季度 第三季度 第四季度
北京 3 16 19 6
东莞 12 20 29 22
(1)根据表中数据完成下面折线统计图。
(2)两个城市的平均气温在第 季度差距最大,第 季度差距最小。
(3)从这幅复式折线统计图上,你还得到了什么信息?(写出1条)
(4)东莞市的王先生计划12月到北京,你觉得需要提醒他注意什么事项呢?
2020-2021学年山东省聊城市冠县五年级(下)期末数学试卷
参考答案与试题解析
一、计算题。(19分)
1.(4分)直接写出得数。
= = = =
= = = =
【答案】;;;1;1;;1;。
【分析】根据分数加减法的计算方法进行计算。
【解答】解:
= = = =8
=1 = =1 =
2.(9分)脱式计算。(能简算的要简算)
【答案】1,1.4,1。
【分析】第1题,利用加法结合律解答;
第2题,利用减法的性质解答;
第3题,利用加法交换律和结合律解答。
【解答】解:++
=+(+)
=+2
=1
2.4﹣﹣
=2.8﹣(+)
=8.4﹣1
=2.4
++﹣
=++(﹣)
=8+
=7
3.(6分)解方程。
x+
【答案】x=1;x=;x=。
【分析】根据等式的性质,方程两端同时减去,算出方程的解。
根据等式的性质,方程两端同时加上,算出方程的解。
根据等式的性质,方程两端同时加上,再同时减去,算出方程的解。
【解答】解:x+=
x+﹣=﹣
x=1
x﹣=
x﹣+=+
x=
x+﹣
x+﹣+=2+
x+=
x+﹣=﹣
x=
二、填空题。(27分)
4.(2分)一堆煤3吨,8天烧完,平均每天烧这堆煤的吨.
【答案】见试题解答内容
【分析】把这堆媒的总质量看成单位“1”,8天烧完,那么平均每天烧这堆煤的,再用这堆煤的总质量3吨除以8天,即可求出平均每天烧多少吨.
【解答】解:1÷8=
3÷7=(吨)
答:平均每天烧这堆煤的,平均每天烧吨.
故答案为:,.
5.(4分)= 1.25 (填小数)
【答案】10,28,20,1.25。
【分析】分数的分子相当于被除数,分母相当于除数,再按分数的基本性质解答,分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变。
【解答】解:=5÷4==
故答案为:10,28,1.25。
6.(2分)具有 相反意义 的量,可以用正、负数表示。如果+100表示小明向南走了100米,那么小华向北走了150米 ﹣150 米。
【答案】相反意义,﹣150。
【分析】具有相反意义的量,可以用正、负数表示。题中规定向南走为正,那么向北走就为负,所以向北走150米记作﹣150米。
【解答】解:具有相反意义的量,可以用正。如果+100表示小明向南走了100米,记作﹣150米。
故答案为:相反意义,﹣150。
7.(2分)5个是 ,是 19 个。
【答案】,19。
【分析】把单位“1”平均分成6份,每份是,5个表示其中5份,即;把单位“1”平均分成7份,每份是,表示这样的19份,即19个。
【解答】解:5个是,是19个。
故答案为:,19。
8.(4分)
48秒= 0.8 分 46cm2= 0.46 dm2 3.08m3= 3 m3 80 dm3
【答案】0.8;0.46;3,80。
【分析】低级单位秒化高级单位分除以进率60。
低级单位立方厘米化高级单位立方分米除以进率100。
3.8立方米看作3立方米与0.08立方米之和,把0.08立方米乘进率1000化成80立方分米。
【解答】解:
48秒=0.8分 46cm6=0.46dm2 6.08m3=3m880dm3
故答案为:0.6;0.46;3。
9.(4分)在横线里填上“>”“<”或“=”。
< >
> 0.375 =
【答案】<,>,>,=。
【分析】同分母分数,分子大的分数就大;同分子分数,分母小的分数就大。
【解答】解:
< >
> 0.375=
故答案为:<,>,>,=。
10.(2分)18和54的最大公因数是 18 ,最小公倍数是 54 。
【答案】见试题解答内容
【分析】根据“当两个数成倍数关系时,较大的那个数,是这两个数的最小公倍数,较小的那个数,是这两个数的最大公约数;进行解答即可.
【解答】解:54÷18=3,即54和18是倍数关系,最小公倍数是54;
故答案为:18,54.
11.(1分)一个正方体的棱长是3分米,把它切成两个体积相等的长方体,表面积增加了 18 平方分米。
【答案】18。
【分析】把这个正方体切成2个相同的长方体增加了2个面,所以表面积增加了原来正方体的2个面的面积。
【解答】解:3×3×5=18(平方分米)
答:表面积增加了18平方分米。
故答案为:18。
12.(1分)实验小学从5名候选人中选2人参加象棋比赛,有 10 种不同的选法。
【答案】10。
【分析】每人都和另外的4人可以组合,所以共有4×5=20(种)组合,由于两人之间重复计算了一次,所以实际共有20÷2=10(种)不同的选法。
【解答】解:(5﹣1)×5÷2
=20÷2
=10(种)
答:有10种不同的选法。
故答案为:10。
13.(3分)将两个棱长3厘米的正方体拼成一个长方体。拼成的长方体的棱长总和是 48 厘米,体积是 54 立方厘米,表面积是 90 平方厘米。
【答案】48,54,90。
【分析】根据题意可知,将两个棱长3厘米的正方体拼成一个长方体。拼成的长方体的长是(3×2)厘米,宽和高都是3厘米,根据长方体的棱长总和=(长+宽+高)×4,长方体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入公式解答。
【解答】解:3×2=6(厘米)
(6+3+7)×4
=12×4
=48(厘米)
8×3×3
=18×2
=54(立方厘米)
(6×3+5×3+3×3)×2
=(18+18+9)×5
=45×2
=90(平方厘米)
答:这个长方体的棱长总和是48厘米,体积是54立方厘米。
故答案为:48,54。
14.(2分)一块长方形的布长24分米,宽18分米,要把它裁成正方形手绢(没有剩余) 6 分米,能裁 12 块。
【答案】6;12。
【分析】求出24和18的最大公因数,即为手绢的边长,分别用长和宽除以手绢的边长,将它们的商再相乘,即可求出能裁多少块。
【解答】解:24=2×2×8×3
18=2×4×3
24和18的最大公因数是:2×6=6。
24÷6×(18÷8)
=4×3
=12(块)
答:手绢的边长最长是2分米,能裁12块。
故答案为:6;12。
三、判断题。(对的画“√”,错的画“×”)(6分)
15.(1分)和大小相等,意义也相同。 × (判断对错)
【答案】×
【分析】根据分数的意义解答即可。
【解答】解:表示把单位“6”平均分成4份;
表示把单位“1”平均分成8份,取其中的2份;
和大小相等。
故原题说法错误。
故答案为:×。
16.(1分)在同一数轴上,5和﹣5离0的距离一样长。 √ (判断对错)
【答案】√
【分析】根据数轴知识可知,在同一数轴上,5和﹣5离0的距离都是5,据此解答即可。
【解答】解:分析可知,在同一数轴上。所以原题说法正确。
故答案为:√。
17.(1分)如果是假分数,那么b一定大于a. × .(判断对错)
【答案】见试题解答内容
【分析】根据假分数的意义,分子大于或等于1的分数是假分数,因此,如果是假分数,那么b一定大于或等于a.
【解答】解:根据假分数的意义,如果,那么b一定大于或等于a.
故答案为:×.
18.(1分)约分和通分的依据都是分数的基本性质 √ .(判断对错)
【答案】见试题解答内容
【分析】依据分数的基本性质,即分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变,从而可以正确进行作答.
【解答】解:根据分数的基本性质,异分母的分数可以化成同分母的分数;
约分就是先将分子和分母分解因数,然后分子和分母同时除以它们的最大公约数;
由此看来,约分和通分的依据都是分数的基本性质.
故答案为:√.
19.(1分)18只有2、3、6、9这4个因数。 × (判断对错)
【答案】×
【分析】根据一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;解答即可。
【解答】解:18的因数中除了2、3、2、9外,所以原题说法错误。
故答案为:×。
20.(1分)复式条形统计图的优点是不仅可以清楚的表示数量的多少,而且便于对两组数据进行比较. √ (判断对错)
【答案】√
【分析】条形统计图就是用长条的长度来表示数量的多少,复式条形统计图还能对两种或两种以上的数据进行大小比较。
【解答】解:复式条形统计图的优点是:不仅可以清楚的表示数量的多少,而且便于对两组数据进行比较。
故答案为:√。
四、选择题。(将正确答案的序号填在括号里)(10分)
21.(2分)本学期,我们学习异分母分数的加减时,用到的方法是 A ;我们学习体积单位时,用到的方法是 B 。
A.转化
B.数形结合
C.类推
【答案】A,B。
【分析】我们学习异分母分数的加减时,用到的方法是转化,通过通分,把异分母分数加减法转化成同分母分数加减法;
学习体积单位时,用到的方法是数形结合,把一个大立体图形转化为数个小的立体图形。
【解答】解:本学期,我们学习异分母分数的加减时;我们学习体积单位时。
故答案为:A,B。
22.(2分)用一根68厘米的铁丝正好弯成一个长方体框架,那么这个长方体一组长、宽、高的和是( )厘米。
A.34 B.18 C.17
【答案】C
【分析】依据长方体棱长总和=(长+宽+高)×4解答即可。
【解答】解:长方体棱长总和=(长+宽+高)×4
68÷4=17(厘米)
这个长方体一组长、宽、高的和是17厘米。
故选:C。
23.(2分)分数的分子加上24,要使分数的大小不变( )
A.18 B.27 C.36
【答案】B
【分析】分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变。
【解答】解:8+24=32
32÷8=7
9×4=36
36﹣3=27
分数的分子加上24,分母应该加上27。
故选:B。
24.(2分)下面图形不是正方体展开图的是( )
A. B. C.
【答案】B
【分析】根据正方体展开图的11种特征,图A和图C是“1 4 1”结构,是正方体的展开图;图B不符合正方体展开图的11种特征,不是正方体的展开图.
【解答】解:图A和图C是“1 4 6”结构,是正方体的展开图;
图B不符合正方体展开图的11种特征,不是正方体的展开图.
故选:B.
25.(2分)一个长8分米、宽3分米、高2.5分米的长方体盒子,最多能放( )棱长是1分米的小正方体木块.
A.48 B.52 C.60
【答案】A
【分析】以长为边最多可以放8÷1=8个,以宽为边最多可以放3÷1=3个,以高为边最多可以放2.5÷1=2个…0.5分米,由此即可解答.
【解答】解:长:8÷1=4(个),
宽:3÷1=2(个),
高:2.5÷6=2(个)…0.59分米),
3×3×2=48(个),
答:最多能放48个棱长是6分米的小正方体木块.
故选:A.
五、实践操作。(14分)
26.(4分)先涂一涂,再写出得数。
【答案】
【分析】根据异分母分数加法法则先涂色,再计算。
【解答】解:+=+=
+=+=
27.(4分)如图是学校所在区域的平面图。
(1)学校的位置用数对表示是( 5 , 2 ),小青家的位置用数对表示是( 10 , 2 )。
(2)医院的位置是(7,6),请你在图中标注出来。
【答案】(1)5,2;10,2;
(2)。
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列,第二个数字表示行,即可用数对分别表示出学校、小青家的位置。
(2)同理,即可用数对表示出医院的位置。
【解答】解:(1)学校的位置用数对表示是(5,2),6)。
(2)医院的位置是(7,6)
故答案为:6,2;10,2。
28.(6分)看图回答问题,以雷达站为观测点。
(1)飞机A在雷达站的 北 偏( 西 , 40 )°方向 200 千米处。
(2)另一架飞机B在雷达站北偏东45方向300千米处,标出飞机B的位置。
【答案】(1)北,西,40,200;
(2)。
【分析】(1)根据平面图上方向的辨别“上北下南,左西右东”,以雷达站的位置为观测点即可确定飞机A的方向,根据飞机A与雷达站的图上距离及图中所标注的线段比例尺即可求出飞机A与雷达站的实际距离。
(2)同现,以雷达站的位置为观测点即可确定飞机B的方向,根据飞机B与雷达站的实际距离及图中所标注的线段比例尺即可求出飞机B与雷达站的图上距离,然后即可在图中标出飞机B的位置。
【解答】解:(1)100×2=200(千米)
答:飞机A在雷达站的北偏西40°方向200千米处。
(2)300÷100=3(厘米)
即另一架飞机B在雷达站北偏东45方向图上距离6厘米处,标出飞机B的位置(下图):
故答案为:北,西,40。
六、解决问题。(24分)
29.(6分)一张卡片,小军第一次用了它的,第二次用了它的。
(1)两次一共用了这张卡纸的几分之几?
(2)还剩几分之几?
【答案】(1);(2)。
【分析】(1)用第一次用去的分率加第二次用去的分率即可;
(2)将这张张卡片当作单位“1”,根据分数减法的意义,用单位“1”减去前两次用的分率即可。
【解答】解:(1)+=
答:两次一共用了这张卡纸的。
(2)1﹣=
答:还剩。
30.(8分)某游泳池长是60米,宽是40米,深是2.5米。
(1)建造这个游泳池要挖出土多少立方米?
(2)在游泳池的四周都抹上水泥,抹水泥的面积是多少平方米?
(3)如果给这个游泳池注2米深的水,已知每小时能注水75立方米,需用几小时?
【答案】(1)6000立方米;
(2)2900平方米;
(3)64小时。
【分析】(1)根据长方体的体积公式:V=abh,把数据代入公式解答。
(2)根据无盖长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式解答。
(3)首先根据长方体的体积公式:V=abh,求出注水的体积,然后工作时间=工作量÷工作效率,列式解答。
【解答】解:(1)60×40×2.5
=2400×4.5
=6000(立方米)
答:建造这个游泳池要挖出土6000立方米。
(2)60×40+60×2.5×2+40×2.4×2
=2400+300+200
=2900(平方米)
答:抹水泥的面积是2900平方米。
(3)60×40×2÷75
=4800÷75
=64(小时)
答:需用64小时。
31.(10分)如图是2020年北京市和东莞市四个季度的平均气温统计表。
北京市和东莞市四个季度平均气温统计表
第一季度 第二季度 第三季度 第四季度
北京 3 16 19 6
东莞 12 20 29 22
(1)根据表中数据完成下面折线统计图。
(2)两个城市的平均气温在第 四 季度差距最大,第 二 季度差距最小。
(3)从这幅复式折线统计图上,你还得到了什么信息?(写出1条)
(4)东莞市的王先生计划12月到北京,你觉得需要提醒他注意什么事项呢?
【答案】(1)
(2)四,二;(3)第一季度北京气温是12℃;(答案不唯一)(4)12月北京气温低,应带毛衣。(答案不唯一)
【分析】(1)根据统计表所给数据制作折线统计图;
(2)观察折线统计图相对应的点距离最大气温差距最大,相对应的点距离最小气温差距最小;
(3)分析统计图上的数据解答;(答案不唯一)
(4)12月北京气温低,应带毛衣。(答案不唯一)
【解答】解:(1)
(2)两个城市的平均气温在第四季度差距最大,第二季度差距最小;
(3)第一季度北京气温是12℃;(答案不唯一)
(4)12月北京气温低,应带毛衣
故答案为:四,二。
一、计算题。(19分)
1.(4分)直接写出得数。
= = = =
= = = =
2.(9分)脱式计算。(能简算的要简算)
3.(6分)解方程。
x+
二、填空题。(27分)
4.(2分)一堆煤3吨,8天烧完,平均每天烧这堆煤的吨.
5.(4分)= (填小数)
6.(2分)具有 的量,可以用正、负数表示。如果+100表示小明向南走了100米,那么小华向北走了150米 米。
7.(2分)5个是 ,是 个。
8.(4分)
48秒= 分 46cm2= dm2 3.08m3= m3 dm3
9.(4分)在横线里填上“>”“<”或“=”。
0.375
10.(2分)18和54的最大公因数是 ,最小公倍数是 。
11.(1分)一个正方体的棱长是3分米,把它切成两个体积相等的长方体,表面积增加了 平方分米。
12.(1分)实验小学从5名候选人中选2人参加象棋比赛,有 种不同的选法。
13.(3分)将两个棱长3厘米的正方体拼成一个长方体。拼成的长方体的棱长总和是 厘米,体积是 立方厘米,表面积是 平方厘米。
14.(2分)一块长方形的布长24分米,宽18分米,要把它裁成正方形手绢(没有剩余) 分米,能裁 块。
三、判断题。(对的画“√”,错的画“×”)(6分)
15.(1分)和大小相等,意义也相同。( .)
16.(1分)在同一数轴上,5和﹣5离0的距离一样长。( .)
17.(1分)如果是假分数,那么b一定大于a.( .)
18.(1分)约分和通分的依据都是分数的基本性质( .)
19.(1分)18只有2、3、6、9这4个因数。( .)
20.(1分)复式条形统计图的优点是不仅可以清楚的表示数量的多少,而且便于对两组数据进行比较.( .)
四、选择题。(将正确答案的序号填在括号里)(10分)
21.(2分)本学期,我们学习异分母分数的加减时,用到的方法是 ;我们学习体积单位时,用到的方法是 。
A.转化
B.数形结合
C.类推
22.(2分)用一根68厘米的铁丝正好弯成一个长方体框架,那么这个长方体一组长、宽、高的和是( )厘米。
A.34 B.18 C.17
23.(2分)分数的分子加上24,要使分数的大小不变( )
A.18 B.27 C.36
24.(2分)下面图形不是正方体展开图的是( )
A. B. C.
25.(2分)一个长8分米、宽3分米、高2.5分米的长方体盒子,最多能放( )棱长是1分米的小正方体木块.
A.48 B.52 C.60
五、实践操作。(14分)
26.(4分)先涂一涂,再写出得数。
27.(4分)如图是学校所在区域的平面图。
(1)学校的位置用数对表示是( , ),小青家的位置用数对表示是( , )。
(2)医院的位置是(7,6),请你在图中标注出来。
28.(6分)看图回答问题,以雷达站为观测点。
(1)飞机A在雷达站的 偏( , )°方向 千米处。
(2)另一架飞机B在雷达站北偏东45方向300千米处,标出飞机B的位置。
六、解决问题。(24分)
29.(6分)一张卡片,小军第一次用了它的,第二次用了它的。
(1)两次一共用了这张卡纸的几分之几?
(2)还剩几分之几?
30.(8分)某游泳池长是60米,宽是40米,深是2.5米。
(1)建造这个游泳池要挖出土多少立方米?
(2)在游泳池的四周都抹上水泥,抹水泥的面积是多少平方米?
(3)如果给这个游泳池注2米深的水,已知每小时能注水75立方米,需用几小时?
31.(10分)如图是2020年北京市和东莞市四个季度的平均气温统计表。
北京市和东莞市四个季度平均气温统计表
第一季度 第二季度 第三季度 第四季度
北京 3 16 19 6
东莞 12 20 29 22
(1)根据表中数据完成下面折线统计图。
(2)两个城市的平均气温在第 季度差距最大,第 季度差距最小。
(3)从这幅复式折线统计图上,你还得到了什么信息?(写出1条)
(4)东莞市的王先生计划12月到北京,你觉得需要提醒他注意什么事项呢?
2020-2021学年山东省聊城市冠县五年级(下)期末数学试卷
参考答案与试题解析
一、计算题。(19分)
1.(4分)直接写出得数。
= = = =
= = = =
【答案】;;;1;1;;1;。
【分析】根据分数加减法的计算方法进行计算。
【解答】解:
= = = =8
=1 = =1 =
2.(9分)脱式计算。(能简算的要简算)
【答案】1,1.4,1。
【分析】第1题,利用加法结合律解答;
第2题,利用减法的性质解答;
第3题,利用加法交换律和结合律解答。
【解答】解:++
=+(+)
=+2
=1
2.4﹣﹣
=2.8﹣(+)
=8.4﹣1
=2.4
++﹣
=++(﹣)
=8+
=7
3.(6分)解方程。
x+
【答案】x=1;x=;x=。
【分析】根据等式的性质,方程两端同时减去,算出方程的解。
根据等式的性质,方程两端同时加上,算出方程的解。
根据等式的性质,方程两端同时加上,再同时减去,算出方程的解。
【解答】解:x+=
x+﹣=﹣
x=1
x﹣=
x﹣+=+
x=
x+﹣
x+﹣+=2+
x+=
x+﹣=﹣
x=
二、填空题。(27分)
4.(2分)一堆煤3吨,8天烧完,平均每天烧这堆煤的吨.
【答案】见试题解答内容
【分析】把这堆媒的总质量看成单位“1”,8天烧完,那么平均每天烧这堆煤的,再用这堆煤的总质量3吨除以8天,即可求出平均每天烧多少吨.
【解答】解:1÷8=
3÷7=(吨)
答:平均每天烧这堆煤的,平均每天烧吨.
故答案为:,.
5.(4分)= 1.25 (填小数)
【答案】10,28,20,1.25。
【分析】分数的分子相当于被除数,分母相当于除数,再按分数的基本性质解答,分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变。
【解答】解:=5÷4==
故答案为:10,28,1.25。
6.(2分)具有 相反意义 的量,可以用正、负数表示。如果+100表示小明向南走了100米,那么小华向北走了150米 ﹣150 米。
【答案】相反意义,﹣150。
【分析】具有相反意义的量,可以用正、负数表示。题中规定向南走为正,那么向北走就为负,所以向北走150米记作﹣150米。
【解答】解:具有相反意义的量,可以用正。如果+100表示小明向南走了100米,记作﹣150米。
故答案为:相反意义,﹣150。
7.(2分)5个是 ,是 19 个。
【答案】,19。
【分析】把单位“1”平均分成6份,每份是,5个表示其中5份,即;把单位“1”平均分成7份,每份是,表示这样的19份,即19个。
【解答】解:5个是,是19个。
故答案为:,19。
8.(4分)
48秒= 0.8 分 46cm2= 0.46 dm2 3.08m3= 3 m3 80 dm3
【答案】0.8;0.46;3,80。
【分析】低级单位秒化高级单位分除以进率60。
低级单位立方厘米化高级单位立方分米除以进率100。
3.8立方米看作3立方米与0.08立方米之和,把0.08立方米乘进率1000化成80立方分米。
【解答】解:
48秒=0.8分 46cm6=0.46dm2 6.08m3=3m880dm3
故答案为:0.6;0.46;3。
9.(4分)在横线里填上“>”“<”或“=”。
< >
> 0.375 =
【答案】<,>,>,=。
【分析】同分母分数,分子大的分数就大;同分子分数,分母小的分数就大。
【解答】解:
< >
> 0.375=
故答案为:<,>,>,=。
10.(2分)18和54的最大公因数是 18 ,最小公倍数是 54 。
【答案】见试题解答内容
【分析】根据“当两个数成倍数关系时,较大的那个数,是这两个数的最小公倍数,较小的那个数,是这两个数的最大公约数;进行解答即可.
【解答】解:54÷18=3,即54和18是倍数关系,最小公倍数是54;
故答案为:18,54.
11.(1分)一个正方体的棱长是3分米,把它切成两个体积相等的长方体,表面积增加了 18 平方分米。
【答案】18。
【分析】把这个正方体切成2个相同的长方体增加了2个面,所以表面积增加了原来正方体的2个面的面积。
【解答】解:3×3×5=18(平方分米)
答:表面积增加了18平方分米。
故答案为:18。
12.(1分)实验小学从5名候选人中选2人参加象棋比赛,有 10 种不同的选法。
【答案】10。
【分析】每人都和另外的4人可以组合,所以共有4×5=20(种)组合,由于两人之间重复计算了一次,所以实际共有20÷2=10(种)不同的选法。
【解答】解:(5﹣1)×5÷2
=20÷2
=10(种)
答:有10种不同的选法。
故答案为:10。
13.(3分)将两个棱长3厘米的正方体拼成一个长方体。拼成的长方体的棱长总和是 48 厘米,体积是 54 立方厘米,表面积是 90 平方厘米。
【答案】48,54,90。
【分析】根据题意可知,将两个棱长3厘米的正方体拼成一个长方体。拼成的长方体的长是(3×2)厘米,宽和高都是3厘米,根据长方体的棱长总和=(长+宽+高)×4,长方体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入公式解答。
【解答】解:3×2=6(厘米)
(6+3+7)×4
=12×4
=48(厘米)
8×3×3
=18×2
=54(立方厘米)
(6×3+5×3+3×3)×2
=(18+18+9)×5
=45×2
=90(平方厘米)
答:这个长方体的棱长总和是48厘米,体积是54立方厘米。
故答案为:48,54。
14.(2分)一块长方形的布长24分米,宽18分米,要把它裁成正方形手绢(没有剩余) 6 分米,能裁 12 块。
【答案】6;12。
【分析】求出24和18的最大公因数,即为手绢的边长,分别用长和宽除以手绢的边长,将它们的商再相乘,即可求出能裁多少块。
【解答】解:24=2×2×8×3
18=2×4×3
24和18的最大公因数是:2×6=6。
24÷6×(18÷8)
=4×3
=12(块)
答:手绢的边长最长是2分米,能裁12块。
故答案为:6;12。
三、判断题。(对的画“√”,错的画“×”)(6分)
15.(1分)和大小相等,意义也相同。 × (判断对错)
【答案】×
【分析】根据分数的意义解答即可。
【解答】解:表示把单位“6”平均分成4份;
表示把单位“1”平均分成8份,取其中的2份;
和大小相等。
故原题说法错误。
故答案为:×。
16.(1分)在同一数轴上,5和﹣5离0的距离一样长。 √ (判断对错)
【答案】√
【分析】根据数轴知识可知,在同一数轴上,5和﹣5离0的距离都是5,据此解答即可。
【解答】解:分析可知,在同一数轴上。所以原题说法正确。
故答案为:√。
17.(1分)如果是假分数,那么b一定大于a. × .(判断对错)
【答案】见试题解答内容
【分析】根据假分数的意义,分子大于或等于1的分数是假分数,因此,如果是假分数,那么b一定大于或等于a.
【解答】解:根据假分数的意义,如果,那么b一定大于或等于a.
故答案为:×.
18.(1分)约分和通分的依据都是分数的基本性质 √ .(判断对错)
【答案】见试题解答内容
【分析】依据分数的基本性质,即分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变,从而可以正确进行作答.
【解答】解:根据分数的基本性质,异分母的分数可以化成同分母的分数;
约分就是先将分子和分母分解因数,然后分子和分母同时除以它们的最大公约数;
由此看来,约分和通分的依据都是分数的基本性质.
故答案为:√.
19.(1分)18只有2、3、6、9这4个因数。 × (判断对错)
【答案】×
【分析】根据一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;解答即可。
【解答】解:18的因数中除了2、3、2、9外,所以原题说法错误。
故答案为:×。
20.(1分)复式条形统计图的优点是不仅可以清楚的表示数量的多少,而且便于对两组数据进行比较. √ (判断对错)
【答案】√
【分析】条形统计图就是用长条的长度来表示数量的多少,复式条形统计图还能对两种或两种以上的数据进行大小比较。
【解答】解:复式条形统计图的优点是:不仅可以清楚的表示数量的多少,而且便于对两组数据进行比较。
故答案为:√。
四、选择题。(将正确答案的序号填在括号里)(10分)
21.(2分)本学期,我们学习异分母分数的加减时,用到的方法是 A ;我们学习体积单位时,用到的方法是 B 。
A.转化
B.数形结合
C.类推
【答案】A,B。
【分析】我们学习异分母分数的加减时,用到的方法是转化,通过通分,把异分母分数加减法转化成同分母分数加减法;
学习体积单位时,用到的方法是数形结合,把一个大立体图形转化为数个小的立体图形。
【解答】解:本学期,我们学习异分母分数的加减时;我们学习体积单位时。
故答案为:A,B。
22.(2分)用一根68厘米的铁丝正好弯成一个长方体框架,那么这个长方体一组长、宽、高的和是( )厘米。
A.34 B.18 C.17
【答案】C
【分析】依据长方体棱长总和=(长+宽+高)×4解答即可。
【解答】解:长方体棱长总和=(长+宽+高)×4
68÷4=17(厘米)
这个长方体一组长、宽、高的和是17厘米。
故选:C。
23.(2分)分数的分子加上24,要使分数的大小不变( )
A.18 B.27 C.36
【答案】B
【分析】分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变。
【解答】解:8+24=32
32÷8=7
9×4=36
36﹣3=27
分数的分子加上24,分母应该加上27。
故选:B。
24.(2分)下面图形不是正方体展开图的是( )
A. B. C.
【答案】B
【分析】根据正方体展开图的11种特征,图A和图C是“1 4 1”结构,是正方体的展开图;图B不符合正方体展开图的11种特征,不是正方体的展开图.
【解答】解:图A和图C是“1 4 6”结构,是正方体的展开图;
图B不符合正方体展开图的11种特征,不是正方体的展开图.
故选:B.
25.(2分)一个长8分米、宽3分米、高2.5分米的长方体盒子,最多能放( )棱长是1分米的小正方体木块.
A.48 B.52 C.60
【答案】A
【分析】以长为边最多可以放8÷1=8个,以宽为边最多可以放3÷1=3个,以高为边最多可以放2.5÷1=2个…0.5分米,由此即可解答.
【解答】解:长:8÷1=4(个),
宽:3÷1=2(个),
高:2.5÷6=2(个)…0.59分米),
3×3×2=48(个),
答:最多能放48个棱长是6分米的小正方体木块.
故选:A.
五、实践操作。(14分)
26.(4分)先涂一涂,再写出得数。
【答案】
【分析】根据异分母分数加法法则先涂色,再计算。
【解答】解:+=+=
+=+=
27.(4分)如图是学校所在区域的平面图。
(1)学校的位置用数对表示是( 5 , 2 ),小青家的位置用数对表示是( 10 , 2 )。
(2)医院的位置是(7,6),请你在图中标注出来。
【答案】(1)5,2;10,2;
(2)。
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列,第二个数字表示行,即可用数对分别表示出学校、小青家的位置。
(2)同理,即可用数对表示出医院的位置。
【解答】解:(1)学校的位置用数对表示是(5,2),6)。
(2)医院的位置是(7,6)
故答案为:6,2;10,2。
28.(6分)看图回答问题,以雷达站为观测点。
(1)飞机A在雷达站的 北 偏( 西 , 40 )°方向 200 千米处。
(2)另一架飞机B在雷达站北偏东45方向300千米处,标出飞机B的位置。
【答案】(1)北,西,40,200;
(2)。
【分析】(1)根据平面图上方向的辨别“上北下南,左西右东”,以雷达站的位置为观测点即可确定飞机A的方向,根据飞机A与雷达站的图上距离及图中所标注的线段比例尺即可求出飞机A与雷达站的实际距离。
(2)同现,以雷达站的位置为观测点即可确定飞机B的方向,根据飞机B与雷达站的实际距离及图中所标注的线段比例尺即可求出飞机B与雷达站的图上距离,然后即可在图中标出飞机B的位置。
【解答】解:(1)100×2=200(千米)
答:飞机A在雷达站的北偏西40°方向200千米处。
(2)300÷100=3(厘米)
即另一架飞机B在雷达站北偏东45方向图上距离6厘米处,标出飞机B的位置(下图):
故答案为:北,西,40。
六、解决问题。(24分)
29.(6分)一张卡片,小军第一次用了它的,第二次用了它的。
(1)两次一共用了这张卡纸的几分之几?
(2)还剩几分之几?
【答案】(1);(2)。
【分析】(1)用第一次用去的分率加第二次用去的分率即可;
(2)将这张张卡片当作单位“1”,根据分数减法的意义,用单位“1”减去前两次用的分率即可。
【解答】解:(1)+=
答:两次一共用了这张卡纸的。
(2)1﹣=
答:还剩。
30.(8分)某游泳池长是60米,宽是40米,深是2.5米。
(1)建造这个游泳池要挖出土多少立方米?
(2)在游泳池的四周都抹上水泥,抹水泥的面积是多少平方米?
(3)如果给这个游泳池注2米深的水,已知每小时能注水75立方米,需用几小时?
【答案】(1)6000立方米;
(2)2900平方米;
(3)64小时。
【分析】(1)根据长方体的体积公式:V=abh,把数据代入公式解答。
(2)根据无盖长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式解答。
(3)首先根据长方体的体积公式:V=abh,求出注水的体积,然后工作时间=工作量÷工作效率,列式解答。
【解答】解:(1)60×40×2.5
=2400×4.5
=6000(立方米)
答:建造这个游泳池要挖出土6000立方米。
(2)60×40+60×2.5×2+40×2.4×2
=2400+300+200
=2900(平方米)
答:抹水泥的面积是2900平方米。
(3)60×40×2÷75
=4800÷75
=64(小时)
答:需用64小时。
31.(10分)如图是2020年北京市和东莞市四个季度的平均气温统计表。
北京市和东莞市四个季度平均气温统计表
第一季度 第二季度 第三季度 第四季度
北京 3 16 19 6
东莞 12 20 29 22
(1)根据表中数据完成下面折线统计图。
(2)两个城市的平均气温在第 四 季度差距最大,第 二 季度差距最小。
(3)从这幅复式折线统计图上,你还得到了什么信息?(写出1条)
(4)东莞市的王先生计划12月到北京,你觉得需要提醒他注意什么事项呢?
【答案】(1)
(2)四,二;(3)第一季度北京气温是12℃;(答案不唯一)(4)12月北京气温低,应带毛衣。(答案不唯一)
【分析】(1)根据统计表所给数据制作折线统计图;
(2)观察折线统计图相对应的点距离最大气温差距最大,相对应的点距离最小气温差距最小;
(3)分析统计图上的数据解答;(答案不唯一)
(4)12月北京气温低,应带毛衣。(答案不唯一)
【解答】解:(1)
(2)两个城市的平均气温在第四季度差距最大,第二季度差距最小;
(3)第一季度北京气温是12℃;(答案不唯一)
(4)12月北京气温低,应带毛衣
故答案为:四,二。
同课章节目录
