专题2.9圆的对称性 弧、弦、圆心角直通中考(含解析)2023-2024学年九年级数学上册苏科版专项讲练
文档属性
| 名称 | 专题2.9圆的对称性 弧、弦、圆心角直通中考(含解析)2023-2024学年九年级数学上册苏科版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
专题2.9 圆的对称性(弧、弦、圆心角)(直通中考)
【要点回顾】
1.圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2.圆心角定理的推论:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
一、单选题
(2022·山东聊城·统考中考真题)
1.如图,AB,CD是的弦,延长AB,CD相交于点P.已知,,则的度数是( )
A.30° B.25° C.20° D.10°
(2021·四川巴中·统考中考真题)
2.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A. B. C. D.
(2013·福建南平·中考真题)
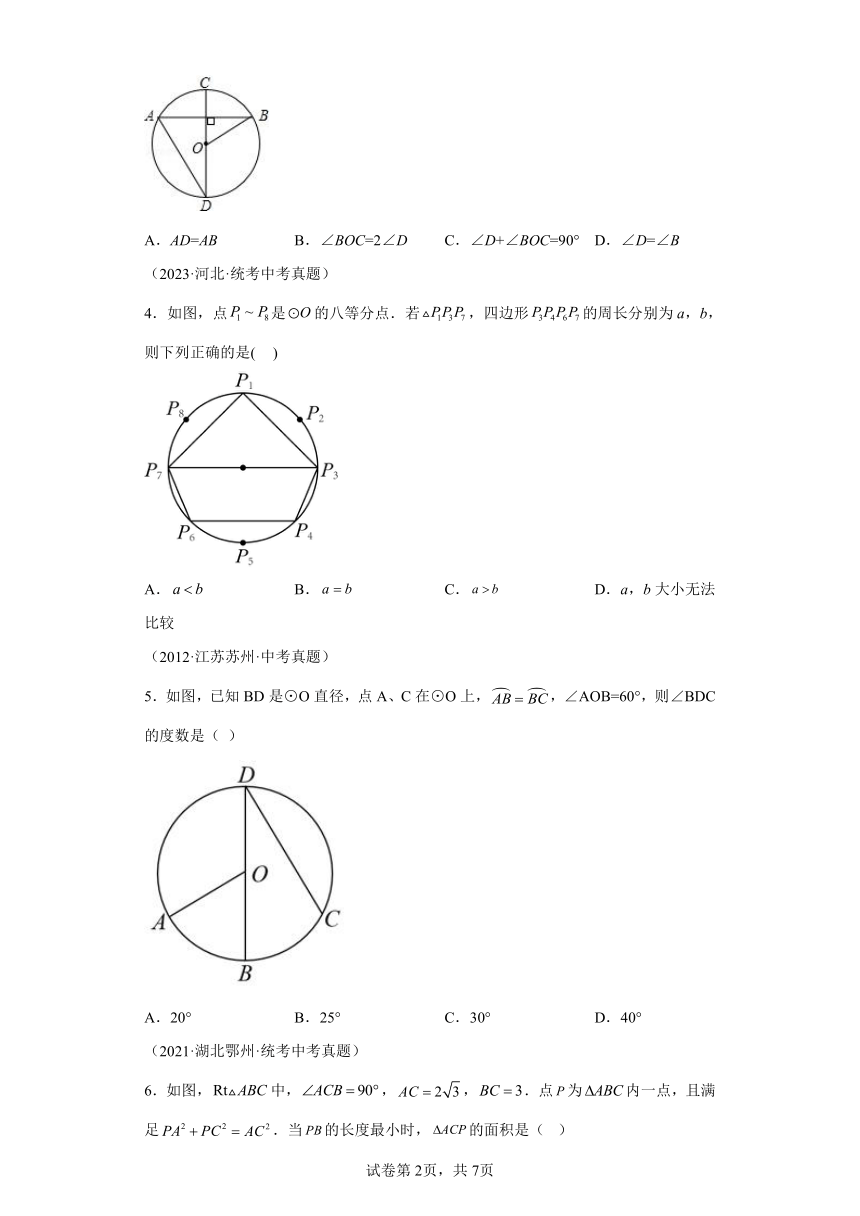
3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AD=AB B.∠BOC=2∠D C.∠D+∠BOC=90° D.∠D=∠B
(2023·河北·统考中考真题)
4.如图,点是的八等分点.若,四边形的周长分别为a,b,则下列正确的是( )
A. B. C. D.a,b大小无法比较
(2012·江苏苏州·中考真题)
5.如图,已知BD是⊙O直径,点A、C在⊙O上,,∠AOB=60°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
(2021·湖北鄂州·统考中考真题)
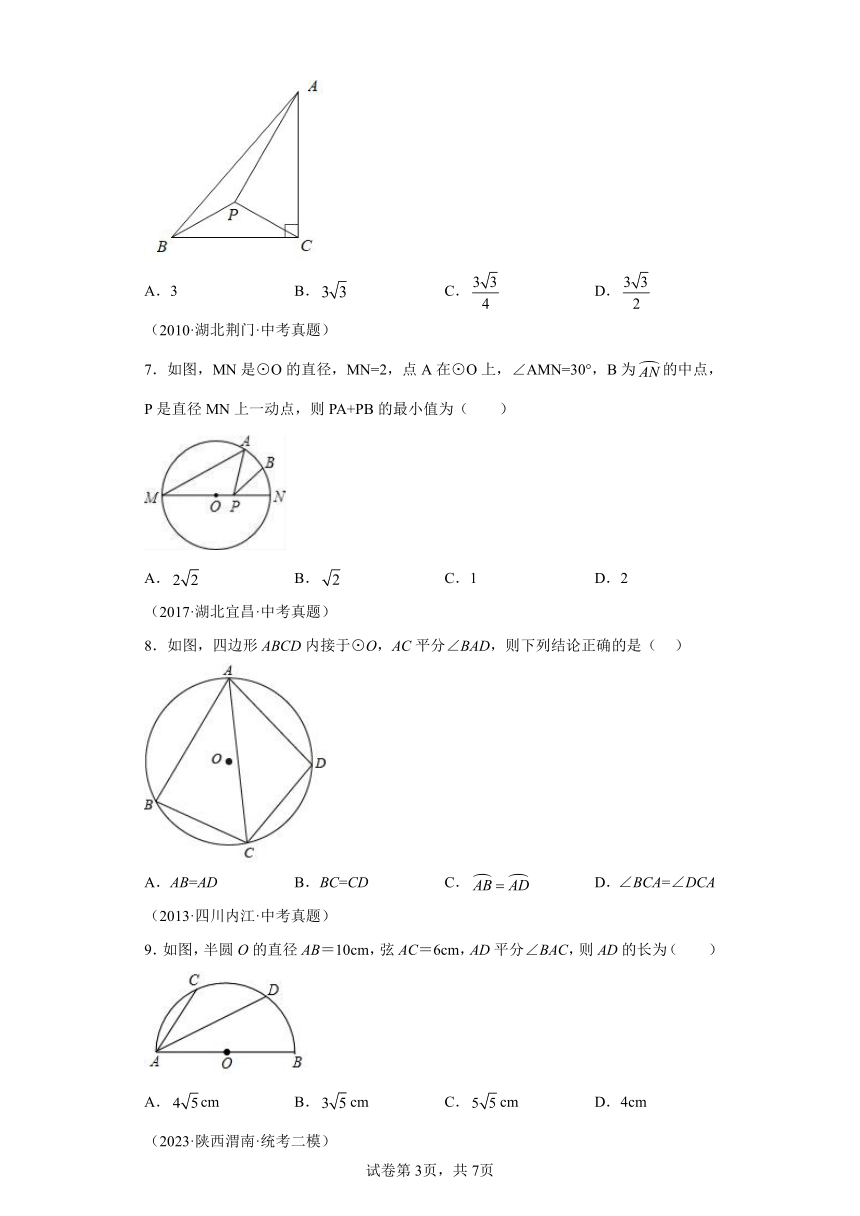
6.如图,中,,,.点为内一点,且满足.当的长度最小时,的面积是( )
A.3 B. C. D.
(2010·湖北荆门·中考真题)
7.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B. C.1 D.2
(2017·湖北宜昌·中考真题)
8.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
(2013·四川内江·中考真题)
9.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.cm B.cm C.cm D.4cm
(2023·陕西渭南·统考二模)
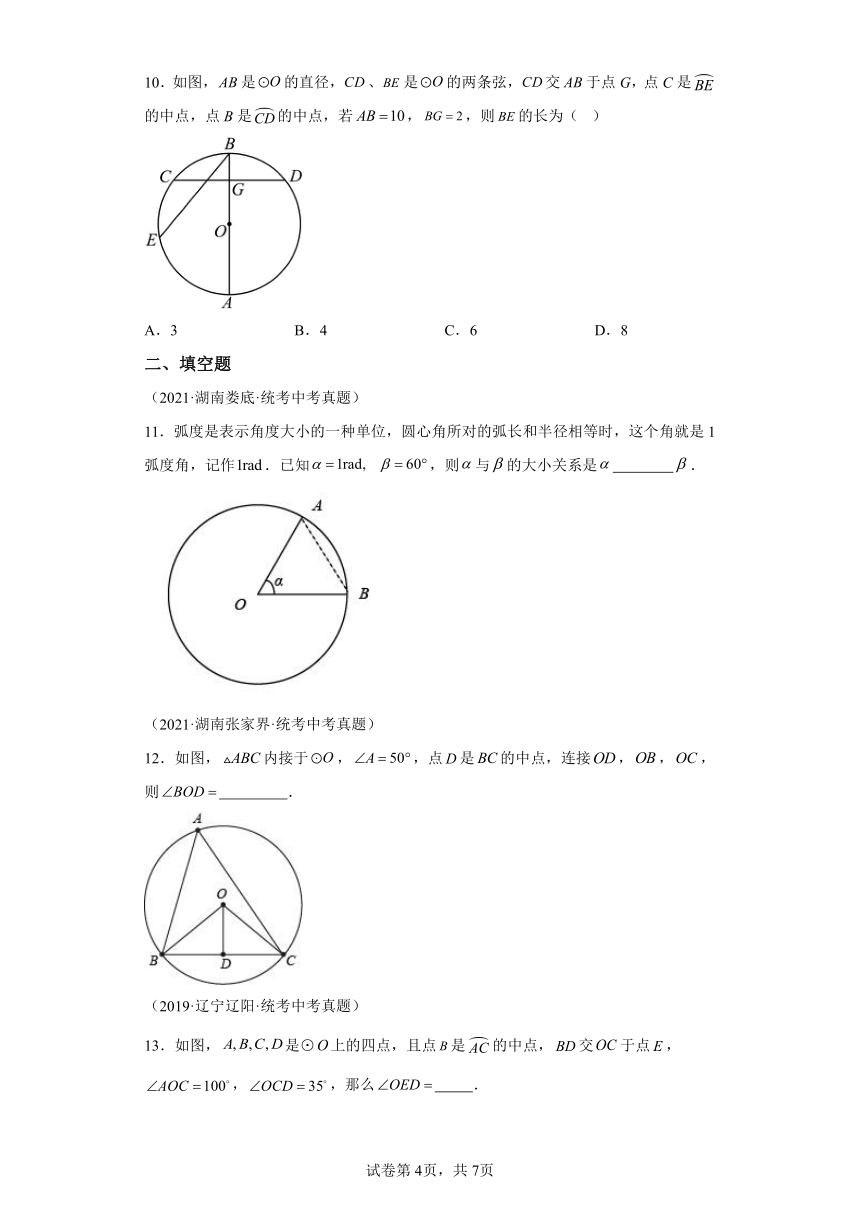
10.如图,是的直径,、是的两条弦,交于点G,点C是的中点,点B是的中点,若,,则的长为( )
A.3 B.4 C.6 D.8
二、填空题
(2021·湖南娄底·统考中考真题)
11.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作.已知,则与的大小关系是 .
(2021·湖南张家界·统考中考真题)
12.如图,内接于,,点是的中点,连接,,,则 .
(2019·辽宁辽阳·统考中考真题)
13.如图,是⊙上的四点,且点是的中点,交于点,,,那么 .
(2018·广东·统考中考真题)
14.同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .
(2010·湖北荆门·中考真题)
15.在⊙O中直径为4,弦AB=2,点C是圆上不同于A、B的点,那么∠ACB度数为 .
(2011·安徽·中考真题)
16.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,CE=1,DE=3,则⊙O的半径是 .
(2023·黑龙江·校联考一模)
17.如图,是的外接圆,,,则的直径为 .
(2022·上海静安·统考二模)
18.如图,已知半圆直径,点C、D三等分半圆弧,那么的面积为 .
三、解答题
(2022·江苏盐城·统考中考真题)
19.证明:垂直于弦的直径平分弦以及弦所对的两条弧.
(2019·四川·统考中考真题)
20.如图,⊙中,弦与相交于点,,连接.
求证:⑴;
⑵.
(2021·山东临沂·统考中考真题)
21.如图,已知在⊙O中, ,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
(2023·湖北武汉·校考模拟预测)
22.如图为圆O的直径,为圆O的弦,C为O上一点,,,垂足为D.
(1)连接,判断与的位置关系,并证明;
(2)若,,求圆O的半径;
(2023·上海闵行·统考二模)
23.如图,在扇形中,点C、D在上,,点F、E分别在半径、上,,连接、.
(1)求证:;
(2)设点Р为的中点,连接、、,线段交于点M、交于点N.如果,求证:四边形是矩形.
(2023·贵州黔南·统考一模)
24.如图,、是圆上的两点,,是的中点.
(1)求证:平分;
(2)延长至,使得,连接,若圆的半径,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】如图,连接OB,OD,AC,先求解,再求解,从而可得,再利用周角的含义可得,从而可得答案.
【详解】解:如图,连接OB,OD,AC,
∵,
∴,
∵,
∴,
∵,,
∴,,
∴,
∴,
∴.
∴的度数20°.
故选:C.
【点睛】本题考查的是圆心角与弧的度数的关系,等腰三角形的性质,三角形的内角和定理的应用,掌握“圆心角与弧的度数的关系”是解本题的关键.
2.C
【分析】连接OA,AC,OC,OC交AB于E,先根据垂径定理求出AE=3,然后证明三角形OAC是等边三角形,从而可以得到∠OAE=30°,再利用三线合一定理求解即可.
【详解】解:如图所示,连接OA,AC,OC,OC交AB于E,
∵C是弧AB的中点,AB=6,
∴OC⊥AB,AE=BE=3,
∵∠ADC=30°,
∴∠AOC=2∠ADC=60°,
又∵OA=OC,
∴△OAC是等边三角形,
∵OC⊥AB,
∴,,
∴
∴
∴圆心O到弦AB的距离为,
故选C.
【点睛】本题主要考查了圆周角与圆心角的关系,等边三角形的性质与判定,勾股定理,垂径定理,解题的关键在于能够熟练掌握相关知识进行求解.
3.B
【分析】根据垂径定理得出弧AD=弧BD,弧AC=弧BC,根据以上结论判断即可.
【详解】A、根据垂径定理不能推出AD=AB,故本选项错误;
B、∵直径CD⊥弦AB,∴弧BC=弧AC,∵弧AC对的圆周角是∠ADC,弧BC对的圆心角是∠BOC,∴∠BOC=2∠ADC,故本选项正确;
C、根据已知推出∠BOC=2∠ADC,不能推出3∠ADC=90°,故本选项错误;
D、根据已知不能推出∠DAB=∠BOC,不能推出∠D=∠B,故本选项错误.
故选B.
【点睛】本题考查了垂径定理的应用,主要考查学生的推理能力和辨析能力.
4.A
【分析】连接,依题意得,,的周长为,四边形的周长为,故,根据的三边关系即可得解.
【详解】连接,
∵点是的八等分点,即
∴,
∴
又∵的周长为,
四边形的周长为,
∴
在中有
∴
故选A.
【点睛】本题考查等弧所对的弦相等,三角形的三边关系等知识,利用作差比较法比较周长大小是解题的关键.
5.C
【详解】∵,∠AOB=60°,
∴∠BDC=∠AOB=30°.
故选C.
6.D
【分析】由题意知,又长度一定,则点P的运动轨迹是以中点O为圆心,长为半径的圆弧,所以当B、P、O三点共线时,BP最短;在中,利用勾股定理可求BO的长,并得到点P是BO的中点,由线段长度即可得到是等边三角形,利用特殊三边关系即可求解.
【详解】解:
取中点O,并以O为圆心,长为半径画圆
由题意知:当B、P、O三点共线时,BP最短
点P是BO的中点
在中,
是等边三角形
在中,
.
【点睛】本题主要考查动点的线段最值问题、点与圆的位置关系和隐形圆问题,属于动态几何综合题型,中档难度.解题的关键是找到动点P的运动轨迹,即隐形圆.
7.B
【分析】作A关于MN的对称点Q,连接MQ,然后根据圆周角定理、圆的对称性质和勾股定理解答即可.
【详解】作A关于MN的对称点Q,连接MQ,BQ,BQ交MN于P,此时AP+PB=QP+PB=QB,
根据两点之间线段最短,PA+PB的最小值为QB的长度,
连接AO,OB,OQ,
∵B为中点,
∴∠BON=∠AMN=30°,
∴∠QON=2∠QMN=2×30°=60°,
∴∠BOQ=30°+60°=90°.
∵直径MN=2,
∴OB=1,
∴BQ==.
则PA+PB的最小值为.
故选B.
【点睛】本题考查了垂径定理、勾股定理、圆周角定理.解答本题的关键是找到点A的对称点,把题目的问题转化为两点之间线段最短解答.
8.B
【分析】根据圆心角,弧,弦的关系对各选项进行逐一判断即可.
【详解】解:A、∵∠ACB与∠ACD的大小关系不确定,
∴AB与AD不一定相等,故此选项不符合题意;
B、∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴BC=CD,,故此选项符合题意;
C、∵∠ACB与∠ACD的大小关系不确定,
∴与不一定相等,不符合题意;
D、∠BCA与∠DCA的大小关系不确定,不符合题意.
故答案为:B.
【点睛】本题考查的是圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
9.A
【详解】试题解析:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴,
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△ODE,
∴OE=AF=AC=3(cm),
在Rt△DOE中,DE==4(cm),
在Rt△ADE中,AD=(cm).
故选A.
10.D
【分析】先根据垂径定理的推论得到,,再利用勾股定理求出,进而得到,再证明,则.
【详解】解:如图所示,连接,
∵点B是的中点,是的直径,
∴,,
∴,
∵,
∴,
∵,
∴,
在中,由勾股定理得,
∴,
∵点C是的中点,
∴,
∴,
∴,
∴,
故选D.
【点睛】本题主要考查了垂径定理的推论,勾股定理,弧与弦之间的关系,正确作出辅助线构造直角三角形是解题的关键.
11.
【分析】根据弧度的定义,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作,当时,三角形为等边三角形,所以圆心角所对的弧长比半径大,即可判断大小.
【详解】解:根据弧度的定义,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作,
当时,易知三角形为等边三角形,弦长等于半径,
圆心角所对的弧长比半径大,
,
故答案是:.
【点睛】本题考查了弧度的定义,解题的关键是:理解弧度的定义,从而利用定义来判断.
12.
【分析】圆上弧长对应的圆周角等于圆心角的一半,再利用等腰三角形三线合一的性质,即可得出答案.
【详解】解:根据圆上弦长对应的圆周角等于圆心角的一半,
,
,
,
为等腰三角形,
又点是的中点,根据等腰三角形三线合一,
为的角平分线,
,
故答案是:.
【点睛】本题考查了弦长所对应的圆周角等于圆心角的一半和等腰三角形三线合一的性质,解题的关键是:根据性质求出,再利用角平分线或三角形全等都能求出解.
13.60°
【分析】根据圆周角与圆心角的关系即可求解.
【详解】解:连接.
∵,
∴,
∴,
∵,,
∴,
故答案为60°.
【点睛】此题主要考查圆周角定理的应用,解题的关键是熟知圆周角定理的性质.
14.50°
【分析】直接利用圆周角定理进行求解即可.
【详解】解:∵弧AB所对的圆心角是100°,
∴弧AB所对的圆周角为50°,
故答案为50°.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
15.60°或120°.
【分析】连接OA、OB,过O作AB的垂线,通过解直角三角形,易求得圆心角∠AOB的度数,然后根据C在优弧AB和劣弧AB上两种情况分类求解.
【详解】解:如图:过O作OD⊥AB于D,连接OA、OB.
Rt△OAD中,OA=2,AD=,
∴∠AOD=60°,∠AOB=120°,
∴∠AEB=∠AOB=60°.
∵四边形AEBF内接于⊙O,
∴∠AFB=180°-∠AEB=120°.
①当点C在优弧AB上时,∠ACB=∠AEB=60°;
②当点C在劣弧AB上时,∠ACB=∠AFB=120°;
故∠ACB的度数为60°或120°.
故答案为:60°或120°.
16.
【分析】过O作OF⊥CD于F,OQ⊥AB于Q,连接OD,由AB=CD,推出OQ=OF根据正方形的判定推出正方形OQEF,求出OF的长,在△OFD中根据勾股定理即可求出OD.
【详解】解:过O作OF⊥CD于F,OQ⊥AB于Q,连接OD,
∵AB=CD,
∴OQ=OF,
∵OF过圆心O,OF⊥CD,
∴CF=DF=2,
∴EF=2-1=1,
∵OF⊥CD,OQ⊥AB,AB⊥CD,
∴∠OQE=∠AEF=∠OFE=90°,
∵OQ=OF,
∴四边形OQEF是正方形,
∴OF=EF=1,
在△OFD中由勾股定理得:OD=
故答案为:.
【点睛】本题主要考查对垂径定理,圆心角、弧、弦之间的关系,勾股定理,正方形的性质和判定等知识点的理解和掌握,能根据性质求出OF和DF的长是解此题的关键.
17.
【分析】连接,,依据是等腰直角三角形,即可得到,进而得出的直径为.
【详解】如图,连接
,
,
是等腰直角三角形,
又,
∴,
∴的直径为,
故答案为: .
【点睛】本题主要考查了圆周角定理和勾股定理,熟知同圆或等圆中,同弧或等弧所对的圆周角的度数是圆心角度数的一半是解题的关键.
18.
【分析】连接OC,OD,过点O作OE⊥CD,垂足为点E,点C、D三等分半圆弧,可知是等边三角形,从而可以证得CD∥AB,所以和的面积相等,利用30°所对的直角三角形的性质和勾股定理,即可求得面积.
【详解】解:连接OC,OD,过点O作OE⊥CD,垂足为点E,如图,
∵点C、D三等分半圆弧,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴是等边三角形,
∴∠CDO=60°,
∴∠CDO=∠BOD,
∴CD∥AB,
∴,
∵OE⊥CD,
∴∠COE=∠COD=30°,
∴,
在中,,
∴.
故答案为:.
【点睛】本题主要考查了弧与圆心角的关系、等边三角形的判定与性质、平行线的判定、30°所对的直角三角形的性质和勾股定理.
19.见解析
【分析】根据命题的题设:垂直于弦的直径,结论:CD平分AB,CD平分 写出已知,求证,再利用等腰三角形的性质,圆心角与弧之间的关系证明即可.
【详解】已知:如图,是的直径,是的弦,,垂足为.
求证:,,.
证明:如图,连接、.
因为 ,,
所以,.
所以,.
所以.
【点睛】本题考查的是命题的证明,圆心角与弧,弦之间的关系,等腰三角形的性质,熟练的运用在同圆与等圆中,相等的圆心角所对的弧相等是解本题的关键.
20.(1)见解析;(2)见解析.
【分析】(1)由AB=CD知,即,据此可得答案;
(2)由知AD=BC,结合∠ADE=∠CBE,∠DAE=∠BCE可证△ADE≌△CBE,从而得出答案.
【详解】证明(1)∵AB=CD,
∴,即,
∴;
(2)∵,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
【点睛】本题主要考查圆心角、弧、弦的关系,圆心角、弧、弦三者的关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
21.(1)见解析;(2)见解析
【分析】(1)连接BD,根据圆周角定理可得∠ADB=∠CBD,根据平行线的判定可得结论;
(2)证明△DEF≌△BCF,得到DE=BC,证明四边形BCDE为平行四边形,再根据得到BC=CD,从而证明菱形.
【详解】解:(1)连接BD,
∵,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)连接CD,
∵AD∥BC,
∴∠EDF=∠CBF,
∵,
∴BC=CD,
∴BF=DF,又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),
∴DE=BC,
∴四边形BCDE是平行四边形,又BC=CD,
∴四边形BCDE是菱形.
【点睛】本题考查了垂径定理,圆周角定理,弧、弦、圆心角的关系,全等三角形的判定和性质,菱形的判定,解题的关键是合理运用垂径定理得到BF=DF.
22.(1),证明见详解
(2)5
【分析】(1),理由如下:延长交于点,连接,再根据圆的基本性质及等腰三角形的性质即可;
(2)由(1)中结论,,,先证明,再根据勾股定理即可.
【详解】(1)解:,理由如下:
延长交于点,连接,
,
,
;
(2)解:由(1)中结论,,
,
,
设的半径为,则,
在中,,即,
解得:,即的半径为5.
【点睛】本题考查圆的基本性质、全等三角形的判定与性质、勾股定理等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
23.(1)见详解
(2)见详解
【分析】(1)由题意易得,则有,然后可证,进而问题可求证;
(2)由(1)可知:,,然后可得扇形关于对称,则有,进而问题可求证.
【详解】(1)证明:∵,是公共弧,
∴,
∴,
∵,,
∴,
∴;
(2)解:如图所示:
由(1)可知:,,
∵点Р为的中点,
∴,
∴扇形关于对称,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形.
【点睛】本题主要考查垂径定理、圆的基本性质及矩形的判定,熟练掌握垂径定理、圆的基本性质及矩形的判定是解题的关键.
24.(1)见解析
(2)
【分析】(1)求出等边三角形和等边,推出,即可得出答案;
(2)求出,再求出,,即可求出答案.
【详解】(1)证明:连接、,
∵,是弧的中点,
∴,
∵,
∴是等边三角形,
∴,同理,
∴,
∴四边形是菱形,
∴平分;
(2)解:∵是等边三角形,
∴,,
又∵,
∴,
∴,
∴,
∴是直角三角形,
∵,,
∴.
【点睛】本题主要考查了圆心角、弧、弦之间的关系、勾股定理、菱形的判定与性质、等边三角形的性质和判定等知识,熟练掌握相关知识是解题关键.
答案第1页,共2页
答案第1页,共2页
【要点回顾】
1.圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2.圆心角定理的推论:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
一、单选题
(2022·山东聊城·统考中考真题)
1.如图,AB,CD是的弦,延长AB,CD相交于点P.已知,,则的度数是( )
A.30° B.25° C.20° D.10°
(2021·四川巴中·统考中考真题)
2.如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A. B. C. D.
(2013·福建南平·中考真题)
3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AD=AB B.∠BOC=2∠D C.∠D+∠BOC=90° D.∠D=∠B
(2023·河北·统考中考真题)
4.如图,点是的八等分点.若,四边形的周长分别为a,b,则下列正确的是( )
A. B. C. D.a,b大小无法比较
(2012·江苏苏州·中考真题)
5.如图,已知BD是⊙O直径,点A、C在⊙O上,,∠AOB=60°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
(2021·湖北鄂州·统考中考真题)
6.如图,中,,,.点为内一点,且满足.当的长度最小时,的面积是( )
A.3 B. C. D.
(2010·湖北荆门·中考真题)
7.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B. C.1 D.2
(2017·湖北宜昌·中考真题)
8.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
(2013·四川内江·中考真题)
9.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.cm B.cm C.cm D.4cm
(2023·陕西渭南·统考二模)
10.如图,是的直径,、是的两条弦,交于点G,点C是的中点,点B是的中点,若,,则的长为( )
A.3 B.4 C.6 D.8
二、填空题
(2021·湖南娄底·统考中考真题)
11.弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作.已知,则与的大小关系是 .
(2021·湖南张家界·统考中考真题)
12.如图,内接于,,点是的中点,连接,,,则 .
(2019·辽宁辽阳·统考中考真题)
13.如图,是⊙上的四点,且点是的中点,交于点,,,那么 .
(2018·广东·统考中考真题)
14.同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .
(2010·湖北荆门·中考真题)
15.在⊙O中直径为4,弦AB=2,点C是圆上不同于A、B的点,那么∠ACB度数为 .
(2011·安徽·中考真题)
16.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,CE=1,DE=3,则⊙O的半径是 .
(2023·黑龙江·校联考一模)
17.如图,是的外接圆,,,则的直径为 .
(2022·上海静安·统考二模)
18.如图,已知半圆直径,点C、D三等分半圆弧,那么的面积为 .
三、解答题
(2022·江苏盐城·统考中考真题)
19.证明:垂直于弦的直径平分弦以及弦所对的两条弧.
(2019·四川·统考中考真题)
20.如图,⊙中,弦与相交于点,,连接.
求证:⑴;
⑵.
(2021·山东临沂·统考中考真题)
21.如图,已知在⊙O中, ,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
(2023·湖北武汉·校考模拟预测)
22.如图为圆O的直径,为圆O的弦,C为O上一点,,,垂足为D.
(1)连接,判断与的位置关系,并证明;
(2)若,,求圆O的半径;
(2023·上海闵行·统考二模)
23.如图,在扇形中,点C、D在上,,点F、E分别在半径、上,,连接、.
(1)求证:;
(2)设点Р为的中点,连接、、,线段交于点M、交于点N.如果,求证:四边形是矩形.
(2023·贵州黔南·统考一模)
24.如图,、是圆上的两点,,是的中点.
(1)求证:平分;
(2)延长至,使得,连接,若圆的半径,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】如图,连接OB,OD,AC,先求解,再求解,从而可得,再利用周角的含义可得,从而可得答案.
【详解】解:如图,连接OB,OD,AC,
∵,
∴,
∵,
∴,
∵,,
∴,,
∴,
∴,
∴.
∴的度数20°.
故选:C.
【点睛】本题考查的是圆心角与弧的度数的关系,等腰三角形的性质,三角形的内角和定理的应用,掌握“圆心角与弧的度数的关系”是解本题的关键.
2.C
【分析】连接OA,AC,OC,OC交AB于E,先根据垂径定理求出AE=3,然后证明三角形OAC是等边三角形,从而可以得到∠OAE=30°,再利用三线合一定理求解即可.
【详解】解:如图所示,连接OA,AC,OC,OC交AB于E,
∵C是弧AB的中点,AB=6,
∴OC⊥AB,AE=BE=3,
∵∠ADC=30°,
∴∠AOC=2∠ADC=60°,
又∵OA=OC,
∴△OAC是等边三角形,
∵OC⊥AB,
∴,,
∴
∴
∴圆心O到弦AB的距离为,
故选C.
【点睛】本题主要考查了圆周角与圆心角的关系,等边三角形的性质与判定,勾股定理,垂径定理,解题的关键在于能够熟练掌握相关知识进行求解.
3.B
【分析】根据垂径定理得出弧AD=弧BD,弧AC=弧BC,根据以上结论判断即可.
【详解】A、根据垂径定理不能推出AD=AB,故本选项错误;
B、∵直径CD⊥弦AB,∴弧BC=弧AC,∵弧AC对的圆周角是∠ADC,弧BC对的圆心角是∠BOC,∴∠BOC=2∠ADC,故本选项正确;
C、根据已知推出∠BOC=2∠ADC,不能推出3∠ADC=90°,故本选项错误;
D、根据已知不能推出∠DAB=∠BOC,不能推出∠D=∠B,故本选项错误.
故选B.
【点睛】本题考查了垂径定理的应用,主要考查学生的推理能力和辨析能力.
4.A
【分析】连接,依题意得,,的周长为,四边形的周长为,故,根据的三边关系即可得解.
【详解】连接,
∵点是的八等分点,即
∴,
∴
又∵的周长为,
四边形的周长为,
∴
在中有
∴
故选A.
【点睛】本题考查等弧所对的弦相等,三角形的三边关系等知识,利用作差比较法比较周长大小是解题的关键.
5.C
【详解】∵,∠AOB=60°,
∴∠BDC=∠AOB=30°.
故选C.
6.D
【分析】由题意知,又长度一定,则点P的运动轨迹是以中点O为圆心,长为半径的圆弧,所以当B、P、O三点共线时,BP最短;在中,利用勾股定理可求BO的长,并得到点P是BO的中点,由线段长度即可得到是等边三角形,利用特殊三边关系即可求解.
【详解】解:
取中点O,并以O为圆心,长为半径画圆
由题意知:当B、P、O三点共线时,BP最短
点P是BO的中点
在中,
是等边三角形
在中,
.
【点睛】本题主要考查动点的线段最值问题、点与圆的位置关系和隐形圆问题,属于动态几何综合题型,中档难度.解题的关键是找到动点P的运动轨迹,即隐形圆.
7.B
【分析】作A关于MN的对称点Q,连接MQ,然后根据圆周角定理、圆的对称性质和勾股定理解答即可.
【详解】作A关于MN的对称点Q,连接MQ,BQ,BQ交MN于P,此时AP+PB=QP+PB=QB,
根据两点之间线段最短,PA+PB的最小值为QB的长度,
连接AO,OB,OQ,
∵B为中点,
∴∠BON=∠AMN=30°,
∴∠QON=2∠QMN=2×30°=60°,
∴∠BOQ=30°+60°=90°.
∵直径MN=2,
∴OB=1,
∴BQ==.
则PA+PB的最小值为.
故选B.
【点睛】本题考查了垂径定理、勾股定理、圆周角定理.解答本题的关键是找到点A的对称点,把题目的问题转化为两点之间线段最短解答.
8.B
【分析】根据圆心角,弧,弦的关系对各选项进行逐一判断即可.
【详解】解:A、∵∠ACB与∠ACD的大小关系不确定,
∴AB与AD不一定相等,故此选项不符合题意;
B、∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴BC=CD,,故此选项符合题意;
C、∵∠ACB与∠ACD的大小关系不确定,
∴与不一定相等,不符合题意;
D、∠BCA与∠DCA的大小关系不确定,不符合题意.
故答案为:B.
【点睛】本题考查的是圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
9.A
【详解】试题解析:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴,
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△ODE,
∴OE=AF=AC=3(cm),
在Rt△DOE中,DE==4(cm),
在Rt△ADE中,AD=(cm).
故选A.
10.D
【分析】先根据垂径定理的推论得到,,再利用勾股定理求出,进而得到,再证明,则.
【详解】解:如图所示,连接,
∵点B是的中点,是的直径,
∴,,
∴,
∵,
∴,
∵,
∴,
在中,由勾股定理得,
∴,
∵点C是的中点,
∴,
∴,
∴,
∴,
故选D.
【点睛】本题主要考查了垂径定理的推论,勾股定理,弧与弦之间的关系,正确作出辅助线构造直角三角形是解题的关键.
11.
【分析】根据弧度的定义,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作,当时,三角形为等边三角形,所以圆心角所对的弧长比半径大,即可判断大小.
【详解】解:根据弧度的定义,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作,
当时,易知三角形为等边三角形,弦长等于半径,
圆心角所对的弧长比半径大,
,
故答案是:.
【点睛】本题考查了弧度的定义,解题的关键是:理解弧度的定义,从而利用定义来判断.
12.
【分析】圆上弧长对应的圆周角等于圆心角的一半,再利用等腰三角形三线合一的性质,即可得出答案.
【详解】解:根据圆上弦长对应的圆周角等于圆心角的一半,
,
,
,
为等腰三角形,
又点是的中点,根据等腰三角形三线合一,
为的角平分线,
,
故答案是:.
【点睛】本题考查了弦长所对应的圆周角等于圆心角的一半和等腰三角形三线合一的性质,解题的关键是:根据性质求出,再利用角平分线或三角形全等都能求出解.
13.60°
【分析】根据圆周角与圆心角的关系即可求解.
【详解】解:连接.
∵,
∴,
∴,
∵,,
∴,
故答案为60°.
【点睛】此题主要考查圆周角定理的应用,解题的关键是熟知圆周角定理的性质.
14.50°
【分析】直接利用圆周角定理进行求解即可.
【详解】解:∵弧AB所对的圆心角是100°,
∴弧AB所对的圆周角为50°,
故答案为50°.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
15.60°或120°.
【分析】连接OA、OB,过O作AB的垂线,通过解直角三角形,易求得圆心角∠AOB的度数,然后根据C在优弧AB和劣弧AB上两种情况分类求解.
【详解】解:如图:过O作OD⊥AB于D,连接OA、OB.
Rt△OAD中,OA=2,AD=,
∴∠AOD=60°,∠AOB=120°,
∴∠AEB=∠AOB=60°.
∵四边形AEBF内接于⊙O,
∴∠AFB=180°-∠AEB=120°.
①当点C在优弧AB上时,∠ACB=∠AEB=60°;
②当点C在劣弧AB上时,∠ACB=∠AFB=120°;
故∠ACB的度数为60°或120°.
故答案为:60°或120°.
16.
【分析】过O作OF⊥CD于F,OQ⊥AB于Q,连接OD,由AB=CD,推出OQ=OF根据正方形的判定推出正方形OQEF,求出OF的长,在△OFD中根据勾股定理即可求出OD.
【详解】解:过O作OF⊥CD于F,OQ⊥AB于Q,连接OD,
∵AB=CD,
∴OQ=OF,
∵OF过圆心O,OF⊥CD,
∴CF=DF=2,
∴EF=2-1=1,
∵OF⊥CD,OQ⊥AB,AB⊥CD,
∴∠OQE=∠AEF=∠OFE=90°,
∵OQ=OF,
∴四边形OQEF是正方形,
∴OF=EF=1,
在△OFD中由勾股定理得:OD=
故答案为:.
【点睛】本题主要考查对垂径定理,圆心角、弧、弦之间的关系,勾股定理,正方形的性质和判定等知识点的理解和掌握,能根据性质求出OF和DF的长是解此题的关键.
17.
【分析】连接,,依据是等腰直角三角形,即可得到,进而得出的直径为.
【详解】如图,连接
,
,
是等腰直角三角形,
又,
∴,
∴的直径为,
故答案为: .
【点睛】本题主要考查了圆周角定理和勾股定理,熟知同圆或等圆中,同弧或等弧所对的圆周角的度数是圆心角度数的一半是解题的关键.
18.
【分析】连接OC,OD,过点O作OE⊥CD,垂足为点E,点C、D三等分半圆弧,可知是等边三角形,从而可以证得CD∥AB,所以和的面积相等,利用30°所对的直角三角形的性质和勾股定理,即可求得面积.
【详解】解:连接OC,OD,过点O作OE⊥CD,垂足为点E,如图,
∵点C、D三等分半圆弧,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴是等边三角形,
∴∠CDO=60°,
∴∠CDO=∠BOD,
∴CD∥AB,
∴,
∵OE⊥CD,
∴∠COE=∠COD=30°,
∴,
在中,,
∴.
故答案为:.
【点睛】本题主要考查了弧与圆心角的关系、等边三角形的判定与性质、平行线的判定、30°所对的直角三角形的性质和勾股定理.
19.见解析
【分析】根据命题的题设:垂直于弦的直径,结论:CD平分AB,CD平分 写出已知,求证,再利用等腰三角形的性质,圆心角与弧之间的关系证明即可.
【详解】已知:如图,是的直径,是的弦,,垂足为.
求证:,,.
证明:如图,连接、.
因为 ,,
所以,.
所以,.
所以.
【点睛】本题考查的是命题的证明,圆心角与弧,弦之间的关系,等腰三角形的性质,熟练的运用在同圆与等圆中,相等的圆心角所对的弧相等是解本题的关键.
20.(1)见解析;(2)见解析.
【分析】(1)由AB=CD知,即,据此可得答案;
(2)由知AD=BC,结合∠ADE=∠CBE,∠DAE=∠BCE可证△ADE≌△CBE,从而得出答案.
【详解】证明(1)∵AB=CD,
∴,即,
∴;
(2)∵,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
【点睛】本题主要考查圆心角、弧、弦的关系,圆心角、弧、弦三者的关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
21.(1)见解析;(2)见解析
【分析】(1)连接BD,根据圆周角定理可得∠ADB=∠CBD,根据平行线的判定可得结论;
(2)证明△DEF≌△BCF,得到DE=BC,证明四边形BCDE为平行四边形,再根据得到BC=CD,从而证明菱形.
【详解】解:(1)连接BD,
∵,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)连接CD,
∵AD∥BC,
∴∠EDF=∠CBF,
∵,
∴BC=CD,
∴BF=DF,又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),
∴DE=BC,
∴四边形BCDE是平行四边形,又BC=CD,
∴四边形BCDE是菱形.
【点睛】本题考查了垂径定理,圆周角定理,弧、弦、圆心角的关系,全等三角形的判定和性质,菱形的判定,解题的关键是合理运用垂径定理得到BF=DF.
22.(1),证明见详解
(2)5
【分析】(1),理由如下:延长交于点,连接,再根据圆的基本性质及等腰三角形的性质即可;
(2)由(1)中结论,,,先证明,再根据勾股定理即可.
【详解】(1)解:,理由如下:
延长交于点,连接,
,
,
;
(2)解:由(1)中结论,,
,
,
设的半径为,则,
在中,,即,
解得:,即的半径为5.
【点睛】本题考查圆的基本性质、全等三角形的判定与性质、勾股定理等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
23.(1)见详解
(2)见详解
【分析】(1)由题意易得,则有,然后可证,进而问题可求证;
(2)由(1)可知:,,然后可得扇形关于对称,则有,进而问题可求证.
【详解】(1)证明:∵,是公共弧,
∴,
∴,
∵,,
∴,
∴;
(2)解:如图所示:
由(1)可知:,,
∵点Р为的中点,
∴,
∴扇形关于对称,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是矩形.
【点睛】本题主要考查垂径定理、圆的基本性质及矩形的判定,熟练掌握垂径定理、圆的基本性质及矩形的判定是解题的关键.
24.(1)见解析
(2)
【分析】(1)求出等边三角形和等边,推出,即可得出答案;
(2)求出,再求出,,即可求出答案.
【详解】(1)证明:连接、,
∵,是弧的中点,
∴,
∵,
∴是等边三角形,
∴,同理,
∴,
∴四边形是菱形,
∴平分;
(2)解:∵是等边三角形,
∴,,
又∵,
∴,
∴,
∴,
∴是直角三角形,
∵,,
∴.
【点睛】本题主要考查了圆心角、弧、弦之间的关系、勾股定理、菱形的判定与性质、等边三角形的性质和判定等知识,熟练掌握相关知识是解题关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
