专题2.23切线的性质与判定 基础练(含解析)2023-2024学年九年级数学上册苏科版专项讲练
文档属性
| 名称 | 专题2.23切线的性质与判定 基础练(含解析)2023-2024学年九年级数学上册苏科版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
专题2.23 切线的性质与判定(基础练)
一、单选题
1.在中,,,,以C为圆心作与AB相切,则的半径长为( )
A.8 B.4 C.9.6 D.4.8
2.下列直线是圆的切线的是( )
A.经过半径外端的直线 B.垂直于半径的直线
C.与圆有公共点的直线 D.圆心到直线的距离等于这个圆的半径长的直线
3.如图,内接于,过A点作直线,当( )时,直线与相切.
A. B. C. D.
4.用直角钢尺检查下列工件是否恰好是半圆环形,则根据图示情况,肯定是半圆环形的工件是( )
A. B. C. D.
5.如图,点A在上,下列条件不能说明是切线的是( )
A. B. C. D.
6.如图,是的直径,C、D是上的点,,过点C作的切线交的延长线于点E,则等于( )
A. B. C. D.
7.如图,在中,为弦,于点,,过点作的切线,交的延长线于点,则( )
A. B. C. D.
8.如图,是的直径,,垂足为,直线与相切于点,交于点,直线交的延长线于点,连接,若,则的度数是( )
A. B. C. D.
9.如图,已知PA与⊙O相切于点A,连接OA,AB是⊙O的弦,且AB⊥OP,垂足为点C.若AP=3,OP=3,则OC的长为( )
A. B. C.2 D.
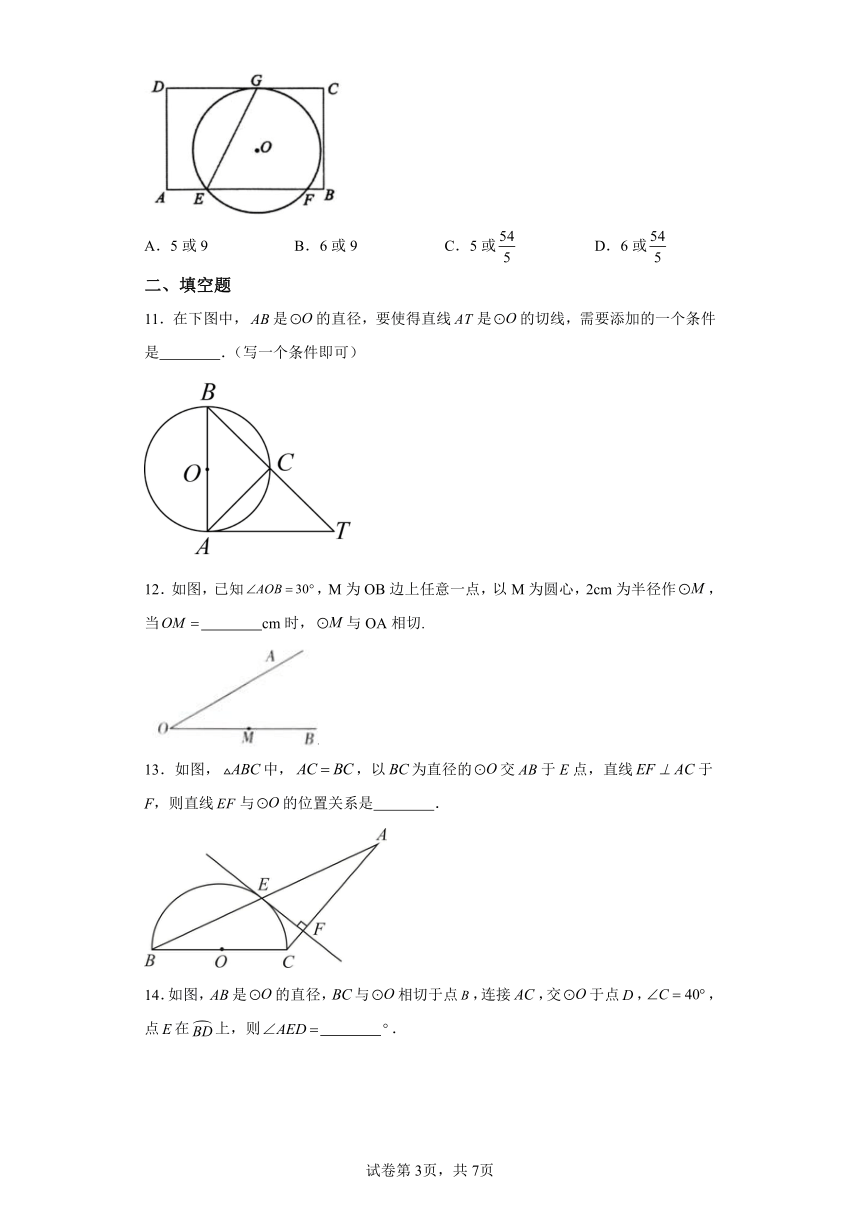
10.如图,在矩形ABCD中,,E是边AB上一点,且.已知经过点E,与边CD所在直线相切于点G(为锐角),与边AB所在直线交于另一点F,且,当边AD或BC所在的直线与相切时,AB的长是( )
A.5或9 B.6或9 C.5或 D.6或
二、填空题
11.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
12.如图,已知,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切.
13.如图,中,,以为直径的交于E点,直线于F,则直线与的位置关系是 .
14.如图,是的直径,与相切于点,连接,交于点,,点在上,则 .
15.如图,圆内接四边形的边过圆心O,过点C的切线与边所在直线垂直于点M,若,则等于 .
16.如图,在中,,与它的边,相切,射线交边于点.当,时,的长等于
17.如图,切于A点,连接交于点C,点D是优弧上一点,若为α,则 (用含α的代数式表示).
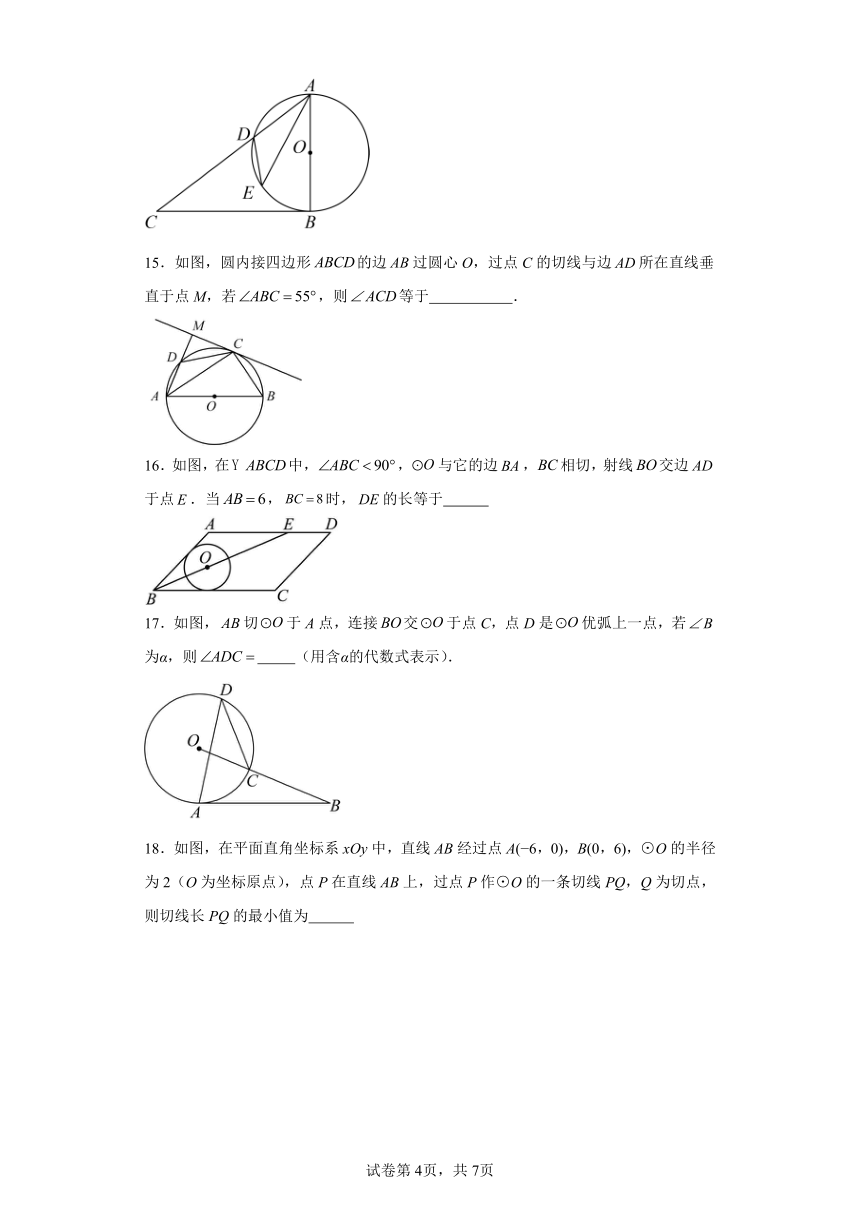
18.如图,在平面直角坐标系xOy中,直线AB经过点A( 6,0),B(0,6),⊙O的半径为2(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
三、解答题
19.如图,已知内接于,是的直径,的平分线交于点,交于点,连接,作,交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径.
20.如图,在中,为的直径,为弦、,.
(1)求的度数;
(2)在图(1)中,P为直径的延长线上一点,且,求证:为的切线.
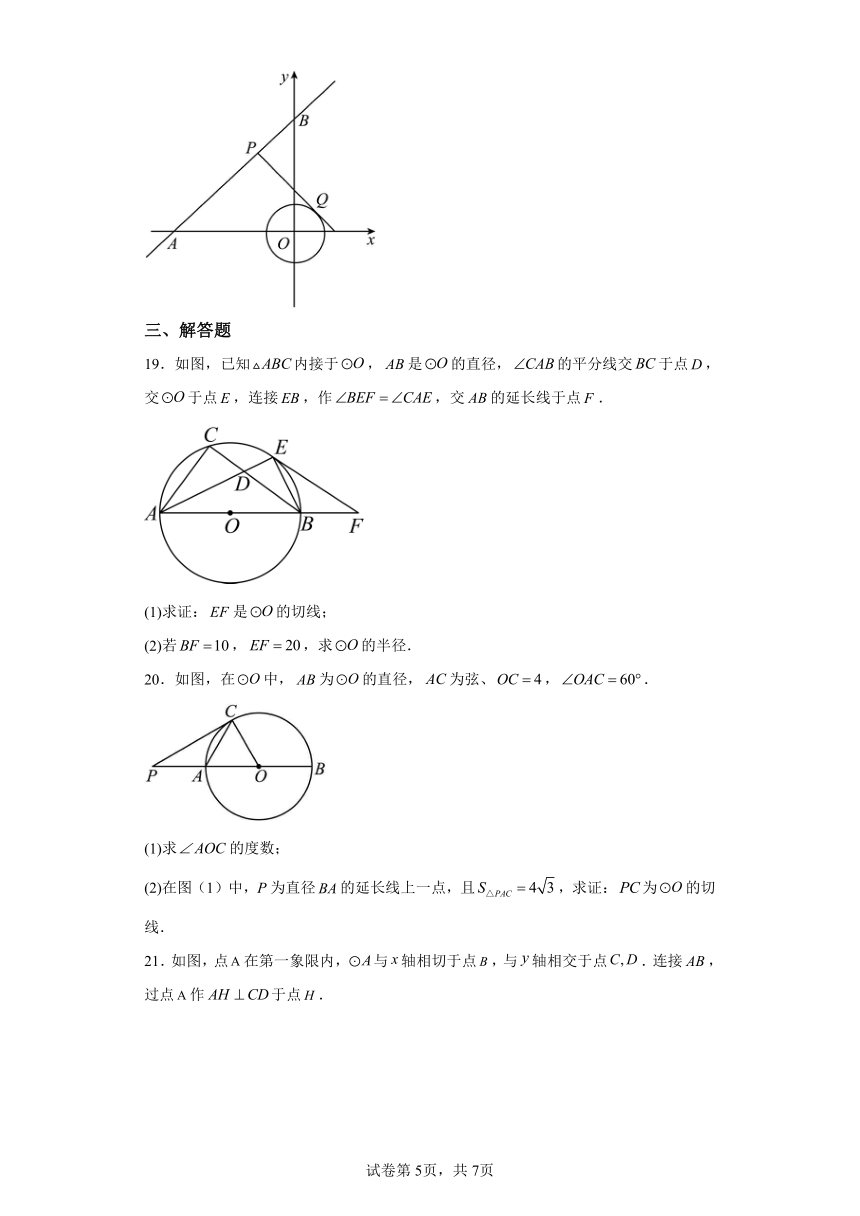
21.如图,点在第一象限内,与轴相切于点,与轴相交于点.连接,过点作于点.
(1)求证:四边形为矩形.
(2)已知的半径为4,,求弦的长.
22.已知:如图,在中,,D是的中点.以为直径作,交边于点P,连接,交于点E.
(1)求证:是的切线;
(2)若是的切线,,求的长.
23.如图1,已知为的直径,点E在上,给出下列信息:①是的切线;②;③平分
(1)请在上述3条信息中选择其中两条作为条件,剩余的一条信息作为结论,组成一个正确的命题,你选择的条件是 、 ,结论是 (只要填写序号),并说明理由;
(2)如图2,在(1)的条件下,交于D,若,求的值.
24.如图1,是的直径,点C是上一点(不与点A,B重合),连接.
(1)请在图1中用无刻度的直尺和圆规作出的中点.(点C,D在线段AB异侧);(保留作图痕迹,不写作法)
(2)如图2,在(1)的条件下,过点D作的切线,分别交的延长线于点E,F.
①求证:;
②过C作于M,交于点N,若,,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】过点C作CD⊥AB于点D,先利用勾股定理求得BC的长,再利用三角形的面积公式求得CD的长即可.
【详解】解:如图,过点C作CD⊥AB于点D,
∵,,,
∴,
∵S△ABC,
∴,
则以C为圆心CD为半径作与AB相切.
故选D.
【点睛】本题主要考查切线的判定,勾股定理,三角形的面积公式,解此题的关键在于熟练掌握其知识点.
2.D
【分析】根据圆的切线的判定定理进行判断即可.
【详解】解:A. 经过半径外端的直线,但直线不一定垂直半径,故不能判断该直线是圆的切线;
B. 垂直于半径的直线,但直线不是经过半径外端,故不能判断该直线是圆的切线;
C. 与圆有公共点的直线,直线与圆相交也有公共点,故不能判断该直线是圆的切线;
D. 圆心到直线的距离等于这个圆的半径长的直线,能判断该直线是圆的切线.
故选D.
【点睛】本题主要考查圆的切线的判定定理,圆的切线必须与半径垂直,且过半径的外端.
3.C
【分析】首先过点O作直径AF,连接BF,根据同弧所对的圆周角相等可得∠C=∠AFB,进而可得到∠BAE=∠F,再根据直径所对的圆周角是90°,可证出∠AFB+∠BAF=90°,再利用等量代换可得∠BAE+∠BAF=90°,进而得到直线DE与⊙O相切.
【详解】解:当时,直线与相切.
理由如下:
作AF交圆O于F点,连接BF.
∵∠F,∠C是同弧AB所对的角,
∴∠C=∠F,
∵∠BAE=∠C,
∴∠BAE=∠F,
∵AF为直径,
∴∠ABF=90°,
∴在三角形ABF中,∠F+∠BAF=90°,
∵∠F=∠BAE,
∴∠BAE+∠BAF=90°,
∴FA⊥DE,
∴直线DE与⊙O相切.
故选:C
.
【点睛】此题主要考查了切线的判定,关键是正确作出辅助线,证明∠BAE+∠BAF=90°.
4.B
【分析】根据切线性质和的圆周角所对的弦是直径可得答案.
【详解】解:A、不能保证弦的另一端与圆相切,即不能保证弦为直径,故不能肯定是半圆环形的工件,不符合题意;
B、图中角是圆周角,故能肯定是半圆环形的工件,符合题意;
C、图中角不是圆周角,故不能肯定是半圆环形的工件,不符合题意;
D、图中角不是圆周角,故不能肯定是半圆环形的工件,不符合题意;
【点睛】本题考查圆周角定理、切线性质,熟知的圆周角所对的弦是直径是解答的关键.
5.D
【分析】根据切线的判定定理即可依次判断.
【详解】A. 由可得AO⊥AP,可判定是切线;,
B. 可判定是切线;
C. 由,可得∠PAO=90°,可判定是切线;
D. 不能判定是切线;
故选D.
【点睛】此题主要考查切线的判定,解题的关键是熟知圆的切线判定定理.
6.A
【分析】如图,连接,由是的切线,可得,,由,可得.
【详解】解:如图,连接,
∵是的切线,
∴,
∴,
∵,
∴,
故选:A.
【点睛】本题考查了切线的性质,圆周角定理,三角形内角和定理.解题的关键在于对知识的熟练掌握.
7.B
【分析】连接,根据等腰三角形的性质得到,由切线的性质得到,于是得到结论.
【详解】解:于,,
,
是的切线,
,
,
故选:B.
【点睛】本题考查了切线的性质,等腰三角形的性质,正确的作出辅助线构造直角三角形是解题的关键.
8.A
【分析】根据垂直的定义及平行线的判定可知,再利用等腰三角形的性质及平行线的性质即可解答.
【详解】解:连接,
∵与相切于,
∴半径,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
故选:.
【点睛】本题考查了垂直的定义,平行线的性质,切线的性质,等腰三角形的性质,掌握平行线的性质及切线的性质是解题的关键.
9.A
【分析】由勾股定理可知OA=3,从而可知∠AOC=45°,所以△OAC是等腰直角三角形,利用勾股定理即可求出OC的长度.
【详解】解:∵AP是⊙O的切线,
∴∠OAP=90°,
∵AP=3,OP=3,
∴由勾股定理可知:OA==3,
∴∠AOC=45°,
∵AB⊥OP,
∴∠OCA=90°,
∴△AOC是等腰直角三角形,OC=AC
∵AO=
∴OC=OA=,
故选:A.
【点睛】此题主要考查切线的性质定理及应用,解题的关键是熟知垂径定理与切线的性质.
10.D
【分析】边BC所在的直线与⊙O相切时,过点G作GN⊥AB,垂足为N,可得EN=NF,由,依据勾股定理求出半径r,根据计算即可;当边AD所在的直线与⊙O相切时,同理可求.
【详解】解:边BC所在的直线与⊙O相切时,
如图,
切点为K,连接OK,过点G作GN⊥AB,垂足为N,
∴EN=NF,
又∵,
∴
设⊙O的半径为r,由OE2=EN2+ON2,
得:r2=16+(8 r)2,
∴r=5,
∴OK=NB=5,
∴EB=9,
又,即,
∴AB=;
当边AD所在的直线与⊙O相切时,切点为H,连接OH,过点G作GN⊥AB,垂足为N,
同理,可得OH=AN=5,
∴AE=1,
又,
∴AB=6,
故选:C.
【点睛】本题考查了切线的性质、勾股定理和垂径定理的综合应用,解答本题的关键在于做好辅助线,利用勾股定理求出对应圆的半径.
11.∠ABT=∠ATB=45°(答案不唯一)
【分析】根据切线的判定条件,只需要得到∠BAT=90°即可求解,因此只需要添加条件:∠ABT=∠ATB=45°即可.
【详解】解:添加条件:∠ABT=∠ATB=45°,
∵∠ABT=∠ATB=45°,
∴∠BAT=90°,
又∵AB是圆O的直径,
∴AT是圆O的切线,
故答案为:∠ABT=∠ATB=45°(答案不唯一).
【点睛】本题主要考查了圆切线的判定,三角形内角和定理,熟知圆切线的判定条件是解题的关键.
12.4
【分析】过M作MN⊥OA于点N,此时以MN为半径的圆与OA相切,根据30°角所对直角边为斜边的一半可得OM的长.
【详解】解:如图,过M作MN⊥OA于点N,
∵MN=2cm,,
∴OM=4cm,
则当OM=4cm时,与OA相切.
故答案为4.
【点睛】本题主要考查切线判定,直角三角形中30°角所对直角边为斜边的一半,解此题的关键在于熟练掌握其知识点.
13.相切
【分析】连接,,由为圆的直径,根据直径所对的圆周角为直角可得为直角,利用垂直的定义可得垂直于,又,根据三线合一得到为的中点,又为直径的中点,可得为三角形的中位线,根据三角形的中位线平行与第三边可得与平行,同时由与垂直,得到为直角,根据两直线平行内错角相等可得为直角,可得为圆的切线,得证.
【详解】证明:连接,,
为圆的直径,
,
,又,
为的中点,又为直径的中点,
为的中位线,
,
,
又,,
,
则为圆的切线.
故答案为:相切.
【点睛】此题考查了切线的判定,涉及的知识有:等腰三角形的性质,圆周角定理,平行线的性质,以及切线的判定定理,切线的判定定理是经过直径的外端点,且与直径垂直的直线为圆的切线,熟练掌握此定理是证明的关键.
14.
【分析】如图所示,连接,由切线的性质得到,进而求出,由是的直径,得到,则,再由同弧所对的圆周角相等即可得到.
【详解】解:如图所示,连接,
∵与相切于点,
∴,
∵,
∴,
∵是的直径,
∴,
∴,
∴,
故答案为:.
【点睛】本题主要考查了切线的性质,圆周角定理,直角三角形的性质等等,正确作出辅助线是解题的关键.
15.##20度
【分析】由圆内接四边形的性质求出,由圆周角定理求出,得出,由过点C的切线与边所在直线垂直于点M,可得,,继而根据三角形的外角性质得出,即可求出的度数.
【详解】解:连接,
∵圆内接四边形的边过圆心O,
∴,
∴,,
∵过点C的切线与边所在直线垂直于点M,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
故答案为:.
【点睛】本题考查了圆内接四边形的性质、圆周角定理、三角形的外角性质等知识;熟练掌握圆内接四边形的性质和圆周角定理是解决问题的关键.
16.2
【分析】根据切线的性质和角平分线的性质可得,根据平行四边形的性质可得,即可推得,根据等角对等边可得,即可求得.
【详解】∵与它的边,相切,
∴点到,的距离相等,
∴是的角平分线,
∴,
∵四边形是平行四边形,
∴,
∴,
∴,
∴,
故,
故答案为:2.
【点睛】本题考查了切线的性质,角平分线的性质,平行四边形的性质,等角对等边,熟练掌握以上性质是解题的关键.
17.
【分析】连接,根据切线的性质,得到,进而得到,再利用圆周角定理即可得解.
【详解】解:连接,
∵切于A点,
∴,
∵为α,
∴,
∴.
故答案为:.
【点睛】本题考查切线的性质,圆周角定理.熟练掌握圆的切线垂直于过切点的半径,同弧所对的圆周角等于圆心角的一半,是解题的关键.
18.
【分析】连接OP.根据勾股定理知PQ2=OP2-OQ2,当OP⊥AB时,线段OP最短,即线段PQ最短.
【详解】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(-6,0)、B(0,6),
∴OA=OB=6,
∴AB=6,
∴OP=AB=3,
∵OQ=2,
∴PQ=,
故答案为:.
【点睛】本题考查了切线的判定与性质、坐标与图形性质以及矩形的性质等知识点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角来解决有关问题.
19.(1)见解析
(2)15
【分析】(1)连接,根据平分,,,证明即可;
(2)设的半径为,则有,在中,,根据勾股定理建立方程,解方程即可求解.
【详解】(1)解:连接,
是的直径,
,即,
平分,
,
,
,
,
,
,
,
是的半径,
是的切线.
(2)设的半径为,
则有,
∵是的切线.
∴,
在中,,
,
解得,
的半径为.
【点睛】本题考查了切线的性质与判定,勾股定理,熟练掌握切线的性质与判定是解题的关键.
20.(1)
(2)见解析
【分析】(1)根据圆的基本性质以及等边三角形的判定与性质求解即可;
(2)作于点,通过面积计算确定,从而求得,进而证得,最终结合点为半径的外端点,证得结论.
【详解】(1)解:在中,,则为等腰三角形,
∵,
∴为等边三角形,
∴;
(2)证:如图所示,作于点,
由(1)知为等边三角形,
∵,
∴,,
∵,,
∴,即:,
∴,
∵,,
∴,
∵,
∴,
∴,
∵点为半径的外端点,
∴为的切线.
【点睛】本题考查圆的基本性质,等边三角形的判定与性质,切线的判定等,掌握圆的基本性质以及切线的判定方法是解题关键.
21.(1)见解析
(2)
【分析】(1)根据切线的性质及有三个角是直角的四边形是矩形判定即可.
(2)根据矩形的性质、垂径定理及圆的性质计算即可.
【详解】(1)证明:∵与轴相切于点,
∴轴.
∵,
∴,
∴四边形是矩形.
(2)如图,连接.
四边形是矩形,
.
在中,,
.
点为圆心,,
.
【点睛】本题考查了矩形的判定,垂径定理,圆的性质,熟练掌握矩形的判定和垂径定理是解题的关键.
22.(1)证明见解析
(2)
【分析】(1)要证明是圆O的切线,只要证明即可;
(2)连接,根据等腰三角形的性质求得的长,再求的长,根据切线的性质求得,最后利用勾股定理求出的长.
【详解】(1)证明:∵,D是的中点,
∴.
又∵是直径,
∴是的切线.
(2)
解:连接.
∵点D是边的中点,,
∴,
∴.
∴,
∵是的切线,O为圆心,
∴.
在中,由勾股定理,得,
∴.
【点睛】本题是圆的综合问题,考查了圆的切线的判定与性质,勾股定理,等腰三角形的性质,掌握这些性质是解决本题的关键.
23.(1)选择的条件是①②,结论是③,理由见解析;选择的条件是①③,结论是②,理由见解析;选择的条件是②③,结论是①,理由见解析
(2)
【分析】(1)选择的条件是①②,结论是③,理由:连接,可得到,再由是的切线可得,从而得到,即可;选择的条件是①③,结论是②,理由:连接,可得到,再由平分可证得,再由是的切线,即可;选择的条件是②③,结论是①,理由:连接,可得到,再由平分可证得,从而得到,即可;
(2)连接,根据圆内接四边形的性质可得,再证得,可得到,从而求出,即可求解.
【详解】(1)解:选择的条件是①②,结论是③,理由如下:
连接,
,
.
是的切线,
.
,
.
,
,
平分.
选择的条件是①③,结论是②,理由如下:
连接,
,
.
平分,
,
,
.
是的切线,
.
;
选择的条件是②③,结论是①,理由如下:
连接,
,
.
平分,
,
,
.
,
.
是半径,
是的切线;
(2)解:如图,连接,
∵四边形是圆内接四边形,
∴,
∵,
∴,
,为的直径,
∴,
平分,
,
∴,
∴,
∵,
∴,
∴,
∵,
∴,解得:或(舍去),
∴,
∴.
【点睛】本题主要考查了切线的性质和判定,圆内接四边形的性质,相似三角形的判定和性质等知识,熟练掌握切线的性质和判定,圆内接四边形的性质,相似三角形的判定和性质是解题的关键.
24.(1)见解析
(2)①见解析;②
【分析】(1)根据角平分线的画法求解即可;
(2)①连接,由圆周角定理证出,由切线的性质得出,则可得出结论;
②过点作于,交于,证出四边形是矩形,得出,求出的长,则由可得出答案.
【详解】(1)解:如图1,
;
(2)①证明:连接,
平分,
,
,
,
又是的切线,
,
,
∴;
②过点作于,交于,
,,
,
又,
四边形是矩形,
,
是的直径,,,
,
,
,
,
.
【点睛】此题是圆的综合题,考查了切线的性质、圆周角定理、勾股定理、三角形的面积等知识,熟记掌握切线的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在中,,,,以C为圆心作与AB相切,则的半径长为( )
A.8 B.4 C.9.6 D.4.8
2.下列直线是圆的切线的是( )
A.经过半径外端的直线 B.垂直于半径的直线
C.与圆有公共点的直线 D.圆心到直线的距离等于这个圆的半径长的直线
3.如图,内接于,过A点作直线,当( )时,直线与相切.
A. B. C. D.
4.用直角钢尺检查下列工件是否恰好是半圆环形,则根据图示情况,肯定是半圆环形的工件是( )
A. B. C. D.
5.如图,点A在上,下列条件不能说明是切线的是( )
A. B. C. D.
6.如图,是的直径,C、D是上的点,,过点C作的切线交的延长线于点E,则等于( )
A. B. C. D.
7.如图,在中,为弦,于点,,过点作的切线,交的延长线于点,则( )
A. B. C. D.
8.如图,是的直径,,垂足为,直线与相切于点,交于点,直线交的延长线于点,连接,若,则的度数是( )
A. B. C. D.
9.如图,已知PA与⊙O相切于点A,连接OA,AB是⊙O的弦,且AB⊥OP,垂足为点C.若AP=3,OP=3,则OC的长为( )
A. B. C.2 D.
10.如图,在矩形ABCD中,,E是边AB上一点,且.已知经过点E,与边CD所在直线相切于点G(为锐角),与边AB所在直线交于另一点F,且,当边AD或BC所在的直线与相切时,AB的长是( )
A.5或9 B.6或9 C.5或 D.6或
二、填空题
11.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
12.如图,已知,M为OB边上任意一点,以M为圆心,2cm为半径作,当 cm时,与OA相切.
13.如图,中,,以为直径的交于E点,直线于F,则直线与的位置关系是 .
14.如图,是的直径,与相切于点,连接,交于点,,点在上,则 .
15.如图,圆内接四边形的边过圆心O,过点C的切线与边所在直线垂直于点M,若,则等于 .
16.如图,在中,,与它的边,相切,射线交边于点.当,时,的长等于
17.如图,切于A点,连接交于点C,点D是优弧上一点,若为α,则 (用含α的代数式表示).
18.如图,在平面直角坐标系xOy中,直线AB经过点A( 6,0),B(0,6),⊙O的半径为2(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
三、解答题
19.如图,已知内接于,是的直径,的平分线交于点,交于点,连接,作,交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径.
20.如图,在中,为的直径,为弦、,.
(1)求的度数;
(2)在图(1)中,P为直径的延长线上一点,且,求证:为的切线.
21.如图,点在第一象限内,与轴相切于点,与轴相交于点.连接,过点作于点.
(1)求证:四边形为矩形.
(2)已知的半径为4,,求弦的长.
22.已知:如图,在中,,D是的中点.以为直径作,交边于点P,连接,交于点E.
(1)求证:是的切线;
(2)若是的切线,,求的长.
23.如图1,已知为的直径,点E在上,给出下列信息:①是的切线;②;③平分
(1)请在上述3条信息中选择其中两条作为条件,剩余的一条信息作为结论,组成一个正确的命题,你选择的条件是 、 ,结论是 (只要填写序号),并说明理由;
(2)如图2,在(1)的条件下,交于D,若,求的值.
24.如图1,是的直径,点C是上一点(不与点A,B重合),连接.
(1)请在图1中用无刻度的直尺和圆规作出的中点.(点C,D在线段AB异侧);(保留作图痕迹,不写作法)
(2)如图2,在(1)的条件下,过点D作的切线,分别交的延长线于点E,F.
①求证:;
②过C作于M,交于点N,若,,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】过点C作CD⊥AB于点D,先利用勾股定理求得BC的长,再利用三角形的面积公式求得CD的长即可.
【详解】解:如图,过点C作CD⊥AB于点D,
∵,,,
∴,
∵S△ABC,
∴,
则以C为圆心CD为半径作与AB相切.
故选D.
【点睛】本题主要考查切线的判定,勾股定理,三角形的面积公式,解此题的关键在于熟练掌握其知识点.
2.D
【分析】根据圆的切线的判定定理进行判断即可.
【详解】解:A. 经过半径外端的直线,但直线不一定垂直半径,故不能判断该直线是圆的切线;
B. 垂直于半径的直线,但直线不是经过半径外端,故不能判断该直线是圆的切线;
C. 与圆有公共点的直线,直线与圆相交也有公共点,故不能判断该直线是圆的切线;
D. 圆心到直线的距离等于这个圆的半径长的直线,能判断该直线是圆的切线.
故选D.
【点睛】本题主要考查圆的切线的判定定理,圆的切线必须与半径垂直,且过半径的外端.
3.C
【分析】首先过点O作直径AF,连接BF,根据同弧所对的圆周角相等可得∠C=∠AFB,进而可得到∠BAE=∠F,再根据直径所对的圆周角是90°,可证出∠AFB+∠BAF=90°,再利用等量代换可得∠BAE+∠BAF=90°,进而得到直线DE与⊙O相切.
【详解】解:当时,直线与相切.
理由如下:
作AF交圆O于F点,连接BF.
∵∠F,∠C是同弧AB所对的角,
∴∠C=∠F,
∵∠BAE=∠C,
∴∠BAE=∠F,
∵AF为直径,
∴∠ABF=90°,
∴在三角形ABF中,∠F+∠BAF=90°,
∵∠F=∠BAE,
∴∠BAE+∠BAF=90°,
∴FA⊥DE,
∴直线DE与⊙O相切.
故选:C
.
【点睛】此题主要考查了切线的判定,关键是正确作出辅助线,证明∠BAE+∠BAF=90°.
4.B
【分析】根据切线性质和的圆周角所对的弦是直径可得答案.
【详解】解:A、不能保证弦的另一端与圆相切,即不能保证弦为直径,故不能肯定是半圆环形的工件,不符合题意;
B、图中角是圆周角,故能肯定是半圆环形的工件,符合题意;
C、图中角不是圆周角,故不能肯定是半圆环形的工件,不符合题意;
D、图中角不是圆周角,故不能肯定是半圆环形的工件,不符合题意;
【点睛】本题考查圆周角定理、切线性质,熟知的圆周角所对的弦是直径是解答的关键.
5.D
【分析】根据切线的判定定理即可依次判断.
【详解】A. 由可得AO⊥AP,可判定是切线;,
B. 可判定是切线;
C. 由,可得∠PAO=90°,可判定是切线;
D. 不能判定是切线;
故选D.
【点睛】此题主要考查切线的判定,解题的关键是熟知圆的切线判定定理.
6.A
【分析】如图,连接,由是的切线,可得,,由,可得.
【详解】解:如图,连接,
∵是的切线,
∴,
∴,
∵,
∴,
故选:A.
【点睛】本题考查了切线的性质,圆周角定理,三角形内角和定理.解题的关键在于对知识的熟练掌握.
7.B
【分析】连接,根据等腰三角形的性质得到,由切线的性质得到,于是得到结论.
【详解】解:于,,
,
是的切线,
,
,
故选:B.
【点睛】本题考查了切线的性质,等腰三角形的性质,正确的作出辅助线构造直角三角形是解题的关键.
8.A
【分析】根据垂直的定义及平行线的判定可知,再利用等腰三角形的性质及平行线的性质即可解答.
【详解】解:连接,
∵与相切于,
∴半径,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
故选:.
【点睛】本题考查了垂直的定义,平行线的性质,切线的性质,等腰三角形的性质,掌握平行线的性质及切线的性质是解题的关键.
9.A
【分析】由勾股定理可知OA=3,从而可知∠AOC=45°,所以△OAC是等腰直角三角形,利用勾股定理即可求出OC的长度.
【详解】解:∵AP是⊙O的切线,
∴∠OAP=90°,
∵AP=3,OP=3,
∴由勾股定理可知:OA==3,
∴∠AOC=45°,
∵AB⊥OP,
∴∠OCA=90°,
∴△AOC是等腰直角三角形,OC=AC
∵AO=
∴OC=OA=,
故选:A.
【点睛】此题主要考查切线的性质定理及应用,解题的关键是熟知垂径定理与切线的性质.
10.D
【分析】边BC所在的直线与⊙O相切时,过点G作GN⊥AB,垂足为N,可得EN=NF,由,依据勾股定理求出半径r,根据计算即可;当边AD所在的直线与⊙O相切时,同理可求.
【详解】解:边BC所在的直线与⊙O相切时,
如图,
切点为K,连接OK,过点G作GN⊥AB,垂足为N,
∴EN=NF,
又∵,
∴
设⊙O的半径为r,由OE2=EN2+ON2,
得:r2=16+(8 r)2,
∴r=5,
∴OK=NB=5,
∴EB=9,
又,即,
∴AB=;
当边AD所在的直线与⊙O相切时,切点为H,连接OH,过点G作GN⊥AB,垂足为N,
同理,可得OH=AN=5,
∴AE=1,
又,
∴AB=6,
故选:C.
【点睛】本题考查了切线的性质、勾股定理和垂径定理的综合应用,解答本题的关键在于做好辅助线,利用勾股定理求出对应圆的半径.
11.∠ABT=∠ATB=45°(答案不唯一)
【分析】根据切线的判定条件,只需要得到∠BAT=90°即可求解,因此只需要添加条件:∠ABT=∠ATB=45°即可.
【详解】解:添加条件:∠ABT=∠ATB=45°,
∵∠ABT=∠ATB=45°,
∴∠BAT=90°,
又∵AB是圆O的直径,
∴AT是圆O的切线,
故答案为:∠ABT=∠ATB=45°(答案不唯一).
【点睛】本题主要考查了圆切线的判定,三角形内角和定理,熟知圆切线的判定条件是解题的关键.
12.4
【分析】过M作MN⊥OA于点N,此时以MN为半径的圆与OA相切,根据30°角所对直角边为斜边的一半可得OM的长.
【详解】解:如图,过M作MN⊥OA于点N,
∵MN=2cm,,
∴OM=4cm,
则当OM=4cm时,与OA相切.
故答案为4.
【点睛】本题主要考查切线判定,直角三角形中30°角所对直角边为斜边的一半,解此题的关键在于熟练掌握其知识点.
13.相切
【分析】连接,,由为圆的直径,根据直径所对的圆周角为直角可得为直角,利用垂直的定义可得垂直于,又,根据三线合一得到为的中点,又为直径的中点,可得为三角形的中位线,根据三角形的中位线平行与第三边可得与平行,同时由与垂直,得到为直角,根据两直线平行内错角相等可得为直角,可得为圆的切线,得证.
【详解】证明:连接,,
为圆的直径,
,
,又,
为的中点,又为直径的中点,
为的中位线,
,
,
又,,
,
则为圆的切线.
故答案为:相切.
【点睛】此题考查了切线的判定,涉及的知识有:等腰三角形的性质,圆周角定理,平行线的性质,以及切线的判定定理,切线的判定定理是经过直径的外端点,且与直径垂直的直线为圆的切线,熟练掌握此定理是证明的关键.
14.
【分析】如图所示,连接,由切线的性质得到,进而求出,由是的直径,得到,则,再由同弧所对的圆周角相等即可得到.
【详解】解:如图所示,连接,
∵与相切于点,
∴,
∵,
∴,
∵是的直径,
∴,
∴,
∴,
故答案为:.
【点睛】本题主要考查了切线的性质,圆周角定理,直角三角形的性质等等,正确作出辅助线是解题的关键.
15.##20度
【分析】由圆内接四边形的性质求出,由圆周角定理求出,得出,由过点C的切线与边所在直线垂直于点M,可得,,继而根据三角形的外角性质得出,即可求出的度数.
【详解】解:连接,
∵圆内接四边形的边过圆心O,
∴,
∴,,
∵过点C的切线与边所在直线垂直于点M,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
故答案为:.
【点睛】本题考查了圆内接四边形的性质、圆周角定理、三角形的外角性质等知识;熟练掌握圆内接四边形的性质和圆周角定理是解决问题的关键.
16.2
【分析】根据切线的性质和角平分线的性质可得,根据平行四边形的性质可得,即可推得,根据等角对等边可得,即可求得.
【详解】∵与它的边,相切,
∴点到,的距离相等,
∴是的角平分线,
∴,
∵四边形是平行四边形,
∴,
∴,
∴,
∴,
故,
故答案为:2.
【点睛】本题考查了切线的性质,角平分线的性质,平行四边形的性质,等角对等边,熟练掌握以上性质是解题的关键.
17.
【分析】连接,根据切线的性质,得到,进而得到,再利用圆周角定理即可得解.
【详解】解:连接,
∵切于A点,
∴,
∵为α,
∴,
∴.
故答案为:.
【点睛】本题考查切线的性质,圆周角定理.熟练掌握圆的切线垂直于过切点的半径,同弧所对的圆周角等于圆心角的一半,是解题的关键.
18.
【分析】连接OP.根据勾股定理知PQ2=OP2-OQ2,当OP⊥AB时,线段OP最短,即线段PQ最短.
【详解】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(-6,0)、B(0,6),
∴OA=OB=6,
∴AB=6,
∴OP=AB=3,
∵OQ=2,
∴PQ=,
故答案为:.
【点睛】本题考查了切线的判定与性质、坐标与图形性质以及矩形的性质等知识点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角来解决有关问题.
19.(1)见解析
(2)15
【分析】(1)连接,根据平分,,,证明即可;
(2)设的半径为,则有,在中,,根据勾股定理建立方程,解方程即可求解.
【详解】(1)解:连接,
是的直径,
,即,
平分,
,
,
,
,
,
,
,
是的半径,
是的切线.
(2)设的半径为,
则有,
∵是的切线.
∴,
在中,,
,
解得,
的半径为.
【点睛】本题考查了切线的性质与判定,勾股定理,熟练掌握切线的性质与判定是解题的关键.
20.(1)
(2)见解析
【分析】(1)根据圆的基本性质以及等边三角形的判定与性质求解即可;
(2)作于点,通过面积计算确定,从而求得,进而证得,最终结合点为半径的外端点,证得结论.
【详解】(1)解:在中,,则为等腰三角形,
∵,
∴为等边三角形,
∴;
(2)证:如图所示,作于点,
由(1)知为等边三角形,
∵,
∴,,
∵,,
∴,即:,
∴,
∵,,
∴,
∵,
∴,
∴,
∵点为半径的外端点,
∴为的切线.
【点睛】本题考查圆的基本性质,等边三角形的判定与性质,切线的判定等,掌握圆的基本性质以及切线的判定方法是解题关键.
21.(1)见解析
(2)
【分析】(1)根据切线的性质及有三个角是直角的四边形是矩形判定即可.
(2)根据矩形的性质、垂径定理及圆的性质计算即可.
【详解】(1)证明:∵与轴相切于点,
∴轴.
∵,
∴,
∴四边形是矩形.
(2)如图,连接.
四边形是矩形,
.
在中,,
.
点为圆心,,
.
【点睛】本题考查了矩形的判定,垂径定理,圆的性质,熟练掌握矩形的判定和垂径定理是解题的关键.
22.(1)证明见解析
(2)
【分析】(1)要证明是圆O的切线,只要证明即可;
(2)连接,根据等腰三角形的性质求得的长,再求的长,根据切线的性质求得,最后利用勾股定理求出的长.
【详解】(1)证明:∵,D是的中点,
∴.
又∵是直径,
∴是的切线.
(2)
解:连接.
∵点D是边的中点,,
∴,
∴.
∴,
∵是的切线,O为圆心,
∴.
在中,由勾股定理,得,
∴.
【点睛】本题是圆的综合问题,考查了圆的切线的判定与性质,勾股定理,等腰三角形的性质,掌握这些性质是解决本题的关键.
23.(1)选择的条件是①②,结论是③,理由见解析;选择的条件是①③,结论是②,理由见解析;选择的条件是②③,结论是①,理由见解析
(2)
【分析】(1)选择的条件是①②,结论是③,理由:连接,可得到,再由是的切线可得,从而得到,即可;选择的条件是①③,结论是②,理由:连接,可得到,再由平分可证得,再由是的切线,即可;选择的条件是②③,结论是①,理由:连接,可得到,再由平分可证得,从而得到,即可;
(2)连接,根据圆内接四边形的性质可得,再证得,可得到,从而求出,即可求解.
【详解】(1)解:选择的条件是①②,结论是③,理由如下:
连接,
,
.
是的切线,
.
,
.
,
,
平分.
选择的条件是①③,结论是②,理由如下:
连接,
,
.
平分,
,
,
.
是的切线,
.
;
选择的条件是②③,结论是①,理由如下:
连接,
,
.
平分,
,
,
.
,
.
是半径,
是的切线;
(2)解:如图,连接,
∵四边形是圆内接四边形,
∴,
∵,
∴,
,为的直径,
∴,
平分,
,
∴,
∴,
∵,
∴,
∴,
∵,
∴,解得:或(舍去),
∴,
∴.
【点睛】本题主要考查了切线的性质和判定,圆内接四边形的性质,相似三角形的判定和性质等知识,熟练掌握切线的性质和判定,圆内接四边形的性质,相似三角形的判定和性质是解题的关键.
24.(1)见解析
(2)①见解析;②
【分析】(1)根据角平分线的画法求解即可;
(2)①连接,由圆周角定理证出,由切线的性质得出,则可得出结论;
②过点作于,交于,证出四边形是矩形,得出,求出的长,则由可得出答案.
【详解】(1)解:如图1,
;
(2)①证明:连接,
平分,
,
,
,
又是的切线,
,
,
∴;
②过点作于,交于,
,,
,
又,
四边形是矩形,
,
是的直径,,,
,
,
,
,
.
【点睛】此题是圆的综合题,考查了切线的性质、圆周角定理、勾股定理、三角形的面积等知识,熟记掌握切线的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
