专题2.27切线长定理 知识梳理与考点分类讲解(含解析)2023-2024学年九年级数学上册苏科版专项讲练
文档属性
| 名称 | 专题2.27切线长定理 知识梳理与考点分类讲解(含解析)2023-2024学年九年级数学上册苏科版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-15 00:00:00 | ||
图片预览


文档简介
专题2.27 切线长定理(知识梳理与考点分类讲解)
【要点一】切线长定理
1.切线长:
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
要点注意:
切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段.
2.切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
要点注意:
切线长定理包含两个结论:线段相等和角相等.
3.圆外切四边形的性质:
圆外切四边形的两组对边之和相等.
【要点二】三角形的内切圆
1.三角形的内切圆:
与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形的内心:
三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
要点注意:
(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;
(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S为三角形的面积,P为三角形的周长,r为内切圆的半径).
(3) 三角形的外心与内心的区别:
名称 确定方法 图形 性质
外心(三角形外接圆的圆心) 三角形三边中垂线的交点 (1)OA=OB=OC;(2)外心不一定在三角形内部
内心(三角形内切圆的圆心) 三角形三条角平分线的交点 (1)到三角形三边距离相等;(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB; (3)内心在三角形内部.
【考点一】切线长定理 求解
【例1】
1.已知PA,PB分别切⊙O于A,B,E为劣弧AB上一点,过E点的切线交PA于C,交PB于D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
【举一反三】
【变式】
2.如图,PA,PB与⊙O相切,切点为A,B,CD与⊙O相切于点E,分别交PA,PB于点D,C.若PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根.
(1)求m的值;
(2)求△PCD的周长.
【考点二】切线长定理 证明
【例2】
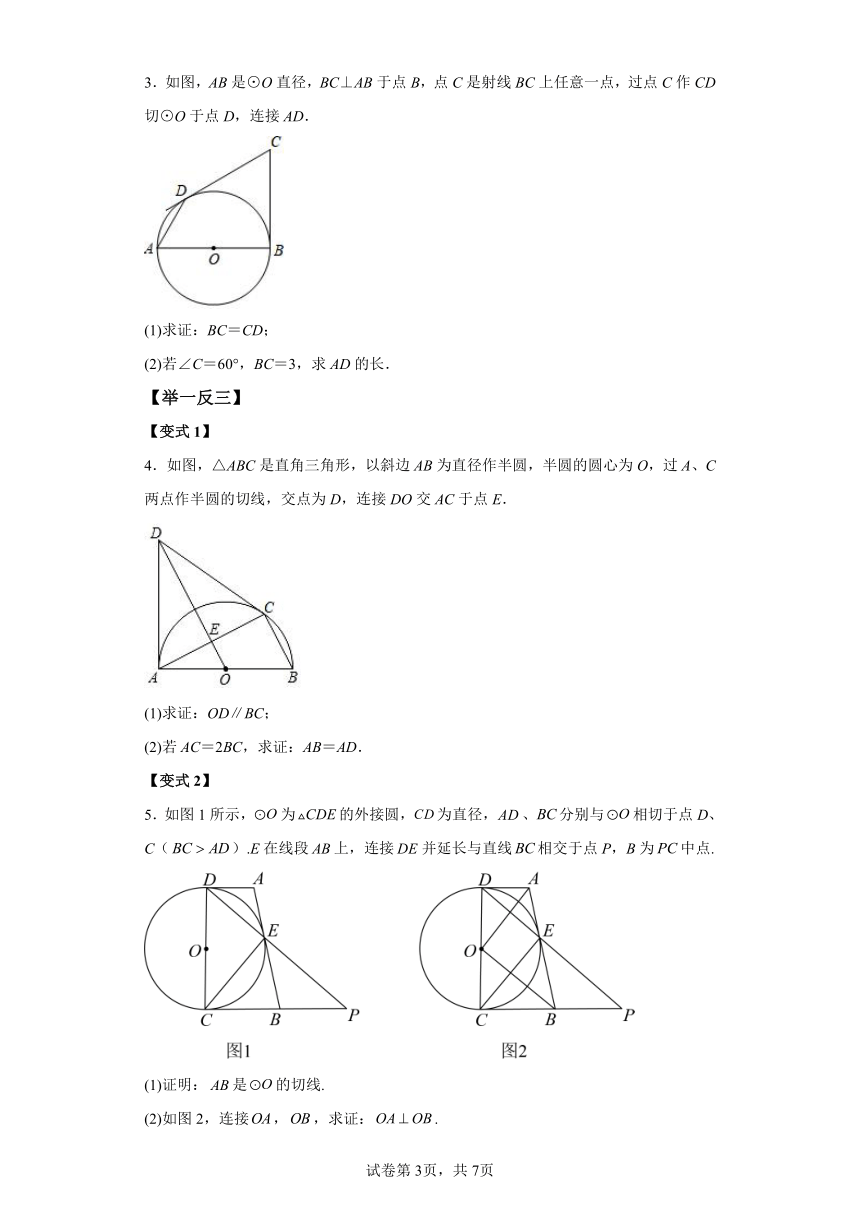
3.如图,AB是⊙O直径,BC⊥AB于点B,点C是射线BC上任意一点,过点C作CD切⊙O于点D,连接AD.
(1)求证:BC=CD;
(2)若∠C=60°,BC=3,求AD的长.
【举一反三】
【变式1】
4.如图,△ABC是直角三角形,以斜边AB为直径作半圆,半圆的圆心为O,过A、C两点作半圆的切线,交点为D,连接DO交AC于点E.
(1)求证:OD∥BC;
(2)若AC=2BC,求证:AB=AD.
【变式2】
5.如图1所示,为的外接圆,为直径,、分别与相切于点D、C().E在线段上,连接并延长与直线相交于点P,B为中点.
(1)证明:是的切线.
(2)如图2,连接,,求证:.
【考点三】切线长定理 三角形的周长、面积与内切半径关系
【例3】
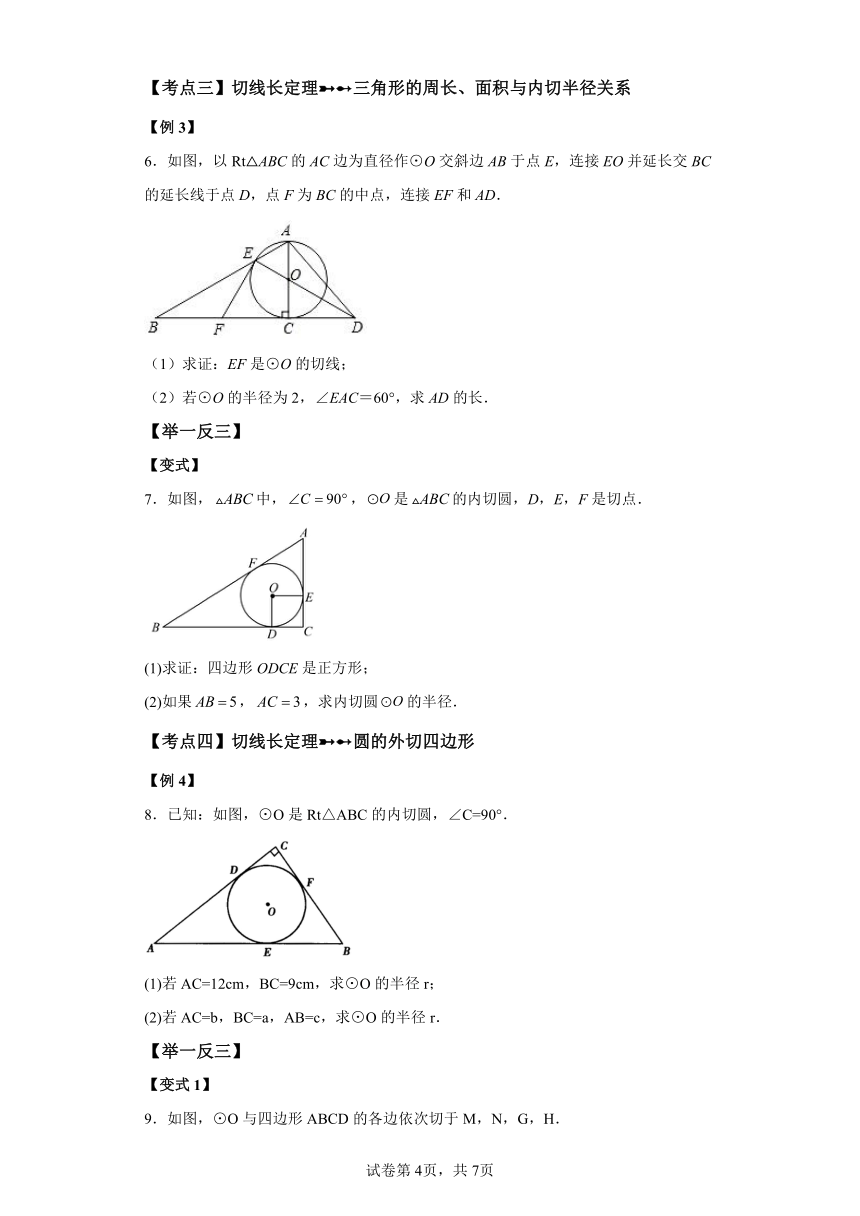
6.如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
【举一反三】
【变式】
7.如图,中,,是的内切圆,D,E,F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果,,求内切圆的半径.
【考点四】切线长定理 圆的外切四边形
【例4】
8.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.
(1)若AC=12cm,BC=9cm,求⊙O的半径r;
(2)若AC=b,BC=a,AB=c,求⊙O的半径r.
【举一反三】
【变式1】
9.如图,⊙O与四边形ABCD的各边依次切于M,N,G,H.
(1)猜想AB+CD与AD+BC有何数量关系,并证明你的猜想;
(2)若四边形ABCD增加条件AD∥BC而成为梯形,梯形的中位线长为m,其他条件不变,试用m表示梯形的周长.
【变式2】
10.如图所示,已知的外切等腰梯形,,梯形中位线为,求证:.
【考点五】切线长定理 三角形的内切圆与外接圆综合
【例5】
11.如图,O是△ABC的外心,I是△ABC的内心,连接AI并延长交BC和⊙O于D,E.
(1)求证:EB=EI;
(2)若AB=8,AC=6,BE=4,求AI的长.
【举一反三】
【变式1】
12.如图,I是的内心,的延长线交的外接圆于点D.
(1)求证:;
(2)求证:;
(3)连接、,求证:点D是的外心.
【变式2】
13.如图,⊙是的内切圆,D,E,F为切点,且,求,,的长.
【考点六】圆的综合题
【例6】
14.如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AE的长.
【举一反三】
【变式1】
15.如图,AC是⊙O的弦,过点O作OP⊥OC交AC于点P,在OP的延长线上取点B,使得BA=BP.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为4,PC=,求线段AB的长.
【变式2】
16.如图1,已知为⊙O的直径,C为⊙O上一点, 平分 ,于点D,并与⊙O交于点E.
(1)求证: 是⊙O的切线;
(2)若 , ,求⊙O的半径;
(3)如图2,F为中点,连接 ,在(2)的条件下,求 的长.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.(1)△PCD的周长为12;(2)∠DOC=65°.
【分析】(1) )连接OE,由切线长定理可得PA=PB=6,AC=CE,BD=DE.再由△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PC+PD+AC+BD=PA+PB即可求得△PCD的周长;(2)根据已知条件易求∠AOB=130°;再证明Rt△AOC≌Rt△EOC,由全等三角形的性质可得∠AOC=∠COE.同理可求得∠DOE=∠BOD,由此可得∠DOC=∠AOB=65°.
【详解】(1)连接OE,
∵PA,PB与⊙O相切,∴PA=PB=6.
同理可得:AC=CE,BD=DE.
∴△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PC+PD+AC+BD=PA+PB=12.
(2)∵PA,PB与⊙O相切,
∴∠OAP=∠OBP=90°.又∵∠P=50°,
∴∠AOB=360°-90°-90°-50°=130°.
在Rt△AOC和Rt△EOC中,
∴Rt△AOC≌Rt△EOC(HL).
∴∠AOC=∠COE.
同理:∠DOE=∠BOD,
∴∠DOC=∠AOB=65°.
【点睛】本题考查了切线的性质定理及切线长定理,熟练运用切线的性质定理及切线长定理是解决问题的关键.
2.(1);(2)2
【分析】(1)根据切线长定理可得,则一元二次方程的判别式为0,进而即可求得的值;
(2)根据(1)的结论求得的长,CD与⊙O相切于点E,则,根据△PCD的周长即可求解.
【详解】解: PA,PB与⊙O相切,
PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根
解得
(2)
PA,PB与⊙O相切, CD与⊙O相切于点E,
△PCD的周长
【点睛】本题考查了切线长定理,一元二次方程根的判别式,解一元二次方程,掌握切线长定理是解题的关键.
3.(1)见解析
(2)
【分析】(1)根据切线长定理证明即可;
(2)根据已知条件可得是等边三角形,根据直径所对的圆周角是直角,含30度角的直角三角形的性质,勾股定理求解即可.
【详解】(1)证明:∵ AB是⊙O直径,BC⊥AB于点B,
是的切线,
CD是的切线,
(2)连接,,
是的切线,, BC=3,
是等边三角形,
,
是直径
【点睛】本题考查了切线长定理,切线的性质,直径所对的圆周角是直角,含30度角的直角三角形的性质,等边三角形的性质与判定,勾股定理,掌握圆的切线的性质是解题的关键.
4.(1)见解析
(2)见解析
【分析】对于(1),连接OC,根据切线的性质得到AD=CD,且OA⊥AD,OC⊥CD,根据全等三角形的性质得到∠ADO=∠CDO,求得DO⊥AC,根据平行线的判定定理即可得到结论;
对于(2),先根据平行线的性质得∠B=∠EOA,进而说明AE=EC,求得∠EOA=∠EAD,再推出BC=AE,根据全等三角形的性质即可得到结论.
【详解】(1)证明:连接OC,如图所示,
∵DA、DC是半圆O的切线,
∴AD=CD,且OA⊥AD,OC⊥CD,
又OA=OC,OD=OD,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
即DO是∠ADC的平分线,
∴DO⊥AC,
又BC⊥AC,
∴OE∥BC;
(2)证明:由(1)知:OE∥BC,DO垂直平分AC,
∴∠B=∠EOA,AE=EC,
又DA⊥AO,
∴∠EOA=∠EAD,
∴∠EAD=∠B.
∵AC=2BC,
∴BC=AE,
∴△ABC≌△DAE(ASA),
∴AB=AD.
【点睛】本题主要考查了圆的切线的性质,平行线的性质和判定,全等三角形的性质和判定等,构造全等三角形是解题的关键.
5.(1)见解析
(2)见解析
【分析】(1)连接,根据直角三角形斜边上的中线的性质以及等边对等角得出,进而根据为切线,, ,得出,即可得证;
(2)根据、、分别与相切于点D、E、C,根据切线长定理得出,,则,,,,即可得出,进而即可得证.
【详解】(1)证明:连接,
∵为直径,
∴.
在中,B为中点,
∴,
∴,
∵,
∴,
又∵为切线,
∴,
∴
∴.
即,
∴是的切线.
(2)证明:∵、、分别与相切于点D、E、C,
∴,,,,
∴,
∴,
∴,
∴,
∴;
【点睛】本题考查了切线的性质与切线长定理,掌握切线的判定方法以及切线长定理是解题的关键.
6.(1)见解析;(2)AD=.
【分析】(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠OEC=∠OCE,再通过Rt△ABC可知∠OEC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)在Rt△OCD中和Rt△ACD中,分别利用勾股定理分别求出CD,AD的长即可 .
【详解】
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°,
∵点F为BC的中点,
∴EF=BF=CF,
∴∠FEC=∠FCE,
∵OE=OC,
∴∠OEC=∠OCE,
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°,
∴EF是⊙O的切线.
(2)解:∵OA=OE,∠EAC=60°,
∴△AOE是等边三角形.
∴∠AOE=60°,
∴∠COD=∠AOE=60°,
∵⊙O的半径为2,
∴OA=OC=2
在Rt△OCD中,∵∠OCD=90°,∠COD=60°,
∴∠ODC=30°,
∴OD=2OC=4,
∴CD=.
在Rt△ACD中,∵∠ACD=90°,AC=4,CD=.
∴AD==.
【点睛】本题主要考查直角三角形、全等三角形的判定与性质以及与圆有关的位置关系 .
7.(1)见解析
(2)1
【分析】(1)根据切线判定定理可得,先证四边形ODCE是矩形,再根据正方形的判定即可求证;
(2)设的半径为r,根据正方形的性质可得,从而得到,,再由切线长定理可得,,然后根据,即可求解.
【详解】(1)证明:∵BC,AC分别切于点D,E,
∴,,
又∵,
∴四边形ODCE是矩形,
又∵,
∴矩形ODCE是正方形.
(2)解:设的半径为r,
∵四边形ODCE是正方形,
∴,
在中,,
∴,,
∵与各边相切于点D,E,F,
∴,,
又∵,
∴,解得
∴内切圆的半径是1.
【点睛】本题主要考查了切线长定理,矩形的判定,正方形的判定和性质,勾股定理,熟练掌握切线长定理,正方形的判定和性质,勾股定理是解题的关键.
8.(1)r=3cm. (2) r=(a+b-c).
【分析】首先设AC、AB、BC与⊙O的切点分别为D、E、F;易证得四边形OFCD是正方形;那么根据切线长定理可得: CD=CF=(AC+BC-AB),由此可求出r的长.
【详解】(1)如图,连接OD,OF;
在Rt△ABC中,∠C=90°,AC=12cm,BC=9cm;
根据勾股定理AB==15cm;
四边形OFCD中,OD=OF,∠ODC=∠OFC=∠C=90°;
则四边形OFCD是正方形;由切线长定理,得:AD=AE,CD=CF,BE=BF;
则CD=CF=(AC+BC-AB);
即:r=(12+9-15)=3cm.
(2)当AC=b,BC=a,AB=c,由以上可得: CD=CF=(AC+BC-AB);
即:r=(a+b-c).则⊙O的半径r为:(a+b-c).
【点睛】此题主要考查直角三角形内切圆的性质及半径的求法.利用切线长定理得出四边形OFCD是正方形是解题关键.
9.(1)AB+CD=AD+BC,证明详见解析;(2)4m.
【分析】(1)由切线长定理,得:AM=AH,BN=BM,CN=CG,DG=DH,所以AB+CD=AD+BC,
(2)AD∥BC,在梯形ABCD中,由梯形的中位线定理得,AD+BC=2m,梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m
【详解】(1)AB+CD=AD+BC
证明:由切线长定理,得:AM=AH,BN=BM,CN=CG,DG=DH,
所以AB+CD=AM+BM+CG+DG=AH+BN+CN+DH=AD+BC,
即AB+CD=AD+BC
(2)AD∥BC,在梯形ABCD中,由梯形的中位线定理得,
AD+BC=2m,
梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m
【点睛】考查了圆外切四边形的性质:圆外切四边形的两组对边和相等;也考查了梯形的中位线定理,梯形的中位线平行于两底,并且等于两底和的一半 .
10.见解析.
【分析】由切线长定理可得AD+BC=AB+CD=2AB,根据梯形中位线定理可得AD+BC=2EF,进而可得EF=AB.
【详解】∵等腰梯形ABCD是的外切等腰梯形,
∴AD+BC=AB+CD=2AB,
∵梯形中位线为EF,
∴AD+BC=2EF,
∴EF=AB.
【点睛】本题考查切线长定理及梯形的中位线,从圆外一点引圆的两条切线,它们的长相等,这一点和圆心的连线平分两条切线的夹角;熟知圆外切四边形对边和相等是解题关键.
11.(1)见解析
(2)AI=4
【分析】(1)欲证明EB=EI,只要证明∠EBI=∠EIB;
(2)连接EC,过点E作EM⊥AB,EN⊥AC交AC的延长线于N,证明△AEM≌△AEN和△BME≌△CNE,再利用勾股定理计算即可解决问题.
【详解】(1)证明:∵I是△ABC的内心,
∴AE平分∠CAB,BI平分∠ABC,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠BIE=∠BAE+∠ABI,∠IBE=∠IBD+∠EBD,
∵∠CBE=∠CAE,
∴∠BIE=∠EBI,
∴EB=EI;
(2)解:连接EC,过点E作EM⊥AB,EN⊥AC交AC的延长线于N,则EM=EN,
∵∠BAE=∠CAE,
∴=,
∴BE=EC=4.
∵AE=AE,EM=EN,
∴△AEM≌△AEN,
∴AM=AN.
∵BE=EC,EM=EN,
△BME≌△CNE(HL),
∴BM=CN.
设BM为x,则8-x=6+x,解得x=1,即BM=1,
∴AM=7.
又∵BE=4,由勾股定理得,EM==.
∴AE==8,
∵EI=BE=4,
∴AI=AE EI=4.
【点睛】本题考查的是三角形的内切圆与内心,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
12.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据三角形内心的定义得,再由圆周角与弧之间的关系即可得证;
(2)连接,证出即可得证;
(3)连接,,,证出即可得证.
【详解】(1)证明:点I是的内心,
平分,
,
,
,
.
(2)证明:如图,连接,
点I是的内心,
平分,平分,
,
又,
,
,,
,
.
(3)证明:如图,连接,,,
,
.
,
∴点D是的外心.
【点睛】本题考查了三角形内心和外心的定义,圆的基本性质中圆周角与弧之间的关系等,理解定义,掌握圆的基本性质,根据题意作出辅助线是解题的关键.
13.
【分析】设,根据切线长定理列出方程即可.
【详解】解:设,
根据切线长定理得:,
解得:,
∴.
【点睛】本题考查了切线长定理,三元一次方程组的应用,根据切线长定理列出方程组是解本题的关键.
14.(1)见解析
(2)见解析
(3)AE=2
【分析】(1)连接OC.证∠D=∠COB.由OD⊥AB,得∠COB+∠COD=90°.可证∠D+∠COD=90°.即∠DCO=90°;
(2)由∠DCE+∠ACO=90°,∠AEO+∠A=90°和∠A=∠ACO,∠DEC=∠AEO,可得∠DEC=∠DCE ,即DE=DC.
(3)先求得OC=4,AB=2OC=8, OE=OD-DE=2,再证△AOE∽△ACB,得.
【详解】(1)证明:连接OC,如图,
∵OA=OC,
∴∠ACO=∠A,
∴∠COB=∠A+∠ACO=2∠A,
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,
∴∠COB+∠COD=90°,
∴∠D+∠COD=90°,即∠DCO=90°,
∴OC⊥DC,
又点C在⊙O上,
∴CD是⊙O的切线;
(2)证明:∵∠DCO=90°,
∴∠DCE+∠ACO=90°,
又∵OD⊥AB,
∴∠AEO+∠A=90°,
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC;
(3)解:∵∠DCO=90°,OD=5,DC=3,
∴OC===4,
∴OA=OC=4,
又DE=DC=3,
∴OE=OD﹣DE=2,
在Rt△AEO中,由勾股定理得:,
∴AE=2.
【点睛】此题考查了切线判定,等腰三角形判定,相似三角形判定,勾股定理,解题的关键是根据所求分析出必要条件,根据相关判定和性质求出有关的角和边的长度.
15.(1)见解析;(2).
【分析】(1)先根据等腰三角形的性质可得∠BPA=∠BAP、∠OAC=∠OCA.再运用等量代换说明∠OAB=90°,即可证明结论;
(2)先由勾股定理可得OP=2, 设AB=x,则OB=x+2.在Rt△AOB中运用勾股定理列方程解答即可.
【详解】解:(1)证明:∵BA=BP,
∴∠BPA=∠BAP.
∵OA=OC,
∴∠OAC=∠OCA.
∵OP⊥OC,
∴∠COP=90°.
∴∠OPC+∠OCP=90°.
∵∠APB=∠OPC,
∴∠BAP+∠OAC=90°.即∠OAB=90°,
∴OA⊥AB.
∵OA为半径,
∴AB为⊙O的切线;
(2)在Rt△OPC中,OC=4,PC=,
∴OP=2.
设AB=x,则OB=x+2.
在Rt△AOB中,,
∴x=3,即AB=3.
【点睛】本题主要考查了圆的性质、圆的切线证明、勾股定理等知识点,灵活运用相关性质、定理成为解答本题的关键.
16.(1)见解析
(2)13
(3)
【分析】(1)连接,利用角平分线的性质,同圆的半径相等,等腰三角形的性质,平行线的判定与性质和圆的切线的判定定理解得即可.
(2)连接 ,过点 作 与点 ,利用切割线定理,垂径定理和矩形的判定与性质解答即可;
(3)连接 , , ,过 作 与点H,利用(2)的结论,等腰直角三角形的判定与性质,圆周角定理,勾股定理解答即可.
【详解】(1)证明:连接,如图
平方
与点D
为的⊙O半径
是⊙O切线
(2)解:连接 ,过点O作于点F,如图,
则
由(1)知,是⊙O的切线
,
由(1)知,
四边形是矩形
(3)解:连接,,,过 作 与点H,如图,
由(2)知:⊙O的半径为13,
为的⊙O直径
为 中点
为等腰直角三角形
【点睛】本题考查角平分线性质,圆周角定理,勾股定理,切割线定理,圆的切线定理以及平行线的判定,熟练掌握这些定理和性质并且画对辅助线是解题的关键.
答案第1页,共2页
答案第1页,共2页
【要点一】切线长定理
1.切线长:
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
要点注意:
切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段.
2.切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
要点注意:
切线长定理包含两个结论:线段相等和角相等.
3.圆外切四边形的性质:
圆外切四边形的两组对边之和相等.
【要点二】三角形的内切圆
1.三角形的内切圆:
与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形的内心:
三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
要点注意:
(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;
(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S为三角形的面积,P为三角形的周长,r为内切圆的半径).
(3) 三角形的外心与内心的区别:
名称 确定方法 图形 性质
外心(三角形外接圆的圆心) 三角形三边中垂线的交点 (1)OA=OB=OC;(2)外心不一定在三角形内部
内心(三角形内切圆的圆心) 三角形三条角平分线的交点 (1)到三角形三边距离相等;(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB; (3)内心在三角形内部.
【考点一】切线长定理 求解
【例1】
1.已知PA,PB分别切⊙O于A,B,E为劣弧AB上一点,过E点的切线交PA于C,交PB于D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
【举一反三】
【变式】
2.如图,PA,PB与⊙O相切,切点为A,B,CD与⊙O相切于点E,分别交PA,PB于点D,C.若PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根.
(1)求m的值;
(2)求△PCD的周长.
【考点二】切线长定理 证明
【例2】
3.如图,AB是⊙O直径,BC⊥AB于点B,点C是射线BC上任意一点,过点C作CD切⊙O于点D,连接AD.
(1)求证:BC=CD;
(2)若∠C=60°,BC=3,求AD的长.
【举一反三】
【变式1】
4.如图,△ABC是直角三角形,以斜边AB为直径作半圆,半圆的圆心为O,过A、C两点作半圆的切线,交点为D,连接DO交AC于点E.
(1)求证:OD∥BC;
(2)若AC=2BC,求证:AB=AD.
【变式2】
5.如图1所示,为的外接圆,为直径,、分别与相切于点D、C().E在线段上,连接并延长与直线相交于点P,B为中点.
(1)证明:是的切线.
(2)如图2,连接,,求证:.
【考点三】切线长定理 三角形的周长、面积与内切半径关系
【例3】
6.如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
【举一反三】
【变式】
7.如图,中,,是的内切圆,D,E,F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果,,求内切圆的半径.
【考点四】切线长定理 圆的外切四边形
【例4】
8.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.
(1)若AC=12cm,BC=9cm,求⊙O的半径r;
(2)若AC=b,BC=a,AB=c,求⊙O的半径r.
【举一反三】
【变式1】
9.如图,⊙O与四边形ABCD的各边依次切于M,N,G,H.
(1)猜想AB+CD与AD+BC有何数量关系,并证明你的猜想;
(2)若四边形ABCD增加条件AD∥BC而成为梯形,梯形的中位线长为m,其他条件不变,试用m表示梯形的周长.
【变式2】
10.如图所示,已知的外切等腰梯形,,梯形中位线为,求证:.
【考点五】切线长定理 三角形的内切圆与外接圆综合
【例5】
11.如图,O是△ABC的外心,I是△ABC的内心,连接AI并延长交BC和⊙O于D,E.
(1)求证:EB=EI;
(2)若AB=8,AC=6,BE=4,求AI的长.
【举一反三】
【变式1】
12.如图,I是的内心,的延长线交的外接圆于点D.
(1)求证:;
(2)求证:;
(3)连接、,求证:点D是的外心.
【变式2】
13.如图,⊙是的内切圆,D,E,F为切点,且,求,,的长.
【考点六】圆的综合题
【例6】
14.如图,AB是⊙O的直径,点C是⊙O上的一点,OD⊥AB交AC于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AE的长.
【举一反三】
【变式1】
15.如图,AC是⊙O的弦,过点O作OP⊥OC交AC于点P,在OP的延长线上取点B,使得BA=BP.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为4,PC=,求线段AB的长.
【变式2】
16.如图1,已知为⊙O的直径,C为⊙O上一点, 平分 ,于点D,并与⊙O交于点E.
(1)求证: 是⊙O的切线;
(2)若 , ,求⊙O的半径;
(3)如图2,F为中点,连接 ,在(2)的条件下,求 的长.
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.(1)△PCD的周长为12;(2)∠DOC=65°.
【分析】(1) )连接OE,由切线长定理可得PA=PB=6,AC=CE,BD=DE.再由△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PC+PD+AC+BD=PA+PB即可求得△PCD的周长;(2)根据已知条件易求∠AOB=130°;再证明Rt△AOC≌Rt△EOC,由全等三角形的性质可得∠AOC=∠COE.同理可求得∠DOE=∠BOD,由此可得∠DOC=∠AOB=65°.
【详解】(1)连接OE,
∵PA,PB与⊙O相切,∴PA=PB=6.
同理可得:AC=CE,BD=DE.
∴△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PC+PD+AC+BD=PA+PB=12.
(2)∵PA,PB与⊙O相切,
∴∠OAP=∠OBP=90°.又∵∠P=50°,
∴∠AOB=360°-90°-90°-50°=130°.
在Rt△AOC和Rt△EOC中,
∴Rt△AOC≌Rt△EOC(HL).
∴∠AOC=∠COE.
同理:∠DOE=∠BOD,
∴∠DOC=∠AOB=65°.
【点睛】本题考查了切线的性质定理及切线长定理,熟练运用切线的性质定理及切线长定理是解决问题的关键.
2.(1);(2)2
【分析】(1)根据切线长定理可得,则一元二次方程的判别式为0,进而即可求得的值;
(2)根据(1)的结论求得的长,CD与⊙O相切于点E,则,根据△PCD的周长即可求解.
【详解】解: PA,PB与⊙O相切,
PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根
解得
(2)
PA,PB与⊙O相切, CD与⊙O相切于点E,
△PCD的周长
【点睛】本题考查了切线长定理,一元二次方程根的判别式,解一元二次方程,掌握切线长定理是解题的关键.
3.(1)见解析
(2)
【分析】(1)根据切线长定理证明即可;
(2)根据已知条件可得是等边三角形,根据直径所对的圆周角是直角,含30度角的直角三角形的性质,勾股定理求解即可.
【详解】(1)证明:∵ AB是⊙O直径,BC⊥AB于点B,
是的切线,
CD是的切线,
(2)连接,,
是的切线,, BC=3,
是等边三角形,
,
是直径
【点睛】本题考查了切线长定理,切线的性质,直径所对的圆周角是直角,含30度角的直角三角形的性质,等边三角形的性质与判定,勾股定理,掌握圆的切线的性质是解题的关键.
4.(1)见解析
(2)见解析
【分析】对于(1),连接OC,根据切线的性质得到AD=CD,且OA⊥AD,OC⊥CD,根据全等三角形的性质得到∠ADO=∠CDO,求得DO⊥AC,根据平行线的判定定理即可得到结论;
对于(2),先根据平行线的性质得∠B=∠EOA,进而说明AE=EC,求得∠EOA=∠EAD,再推出BC=AE,根据全等三角形的性质即可得到结论.
【详解】(1)证明:连接OC,如图所示,
∵DA、DC是半圆O的切线,
∴AD=CD,且OA⊥AD,OC⊥CD,
又OA=OC,OD=OD,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
即DO是∠ADC的平分线,
∴DO⊥AC,
又BC⊥AC,
∴OE∥BC;
(2)证明:由(1)知:OE∥BC,DO垂直平分AC,
∴∠B=∠EOA,AE=EC,
又DA⊥AO,
∴∠EOA=∠EAD,
∴∠EAD=∠B.
∵AC=2BC,
∴BC=AE,
∴△ABC≌△DAE(ASA),
∴AB=AD.
【点睛】本题主要考查了圆的切线的性质,平行线的性质和判定,全等三角形的性质和判定等,构造全等三角形是解题的关键.
5.(1)见解析
(2)见解析
【分析】(1)连接,根据直角三角形斜边上的中线的性质以及等边对等角得出,进而根据为切线,, ,得出,即可得证;
(2)根据、、分别与相切于点D、E、C,根据切线长定理得出,,则,,,,即可得出,进而即可得证.
【详解】(1)证明:连接,
∵为直径,
∴.
在中,B为中点,
∴,
∴,
∵,
∴,
又∵为切线,
∴,
∴
∴.
即,
∴是的切线.
(2)证明:∵、、分别与相切于点D、E、C,
∴,,,,
∴,
∴,
∴,
∴,
∴;
【点睛】本题考查了切线的性质与切线长定理,掌握切线的判定方法以及切线长定理是解题的关键.
6.(1)见解析;(2)AD=.
【分析】(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠OEC=∠OCE,再通过Rt△ABC可知∠OEC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)在Rt△OCD中和Rt△ACD中,分别利用勾股定理分别求出CD,AD的长即可 .
【详解】
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°,
∵点F为BC的中点,
∴EF=BF=CF,
∴∠FEC=∠FCE,
∵OE=OC,
∴∠OEC=∠OCE,
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°,
∴EF是⊙O的切线.
(2)解:∵OA=OE,∠EAC=60°,
∴△AOE是等边三角形.
∴∠AOE=60°,
∴∠COD=∠AOE=60°,
∵⊙O的半径为2,
∴OA=OC=2
在Rt△OCD中,∵∠OCD=90°,∠COD=60°,
∴∠ODC=30°,
∴OD=2OC=4,
∴CD=.
在Rt△ACD中,∵∠ACD=90°,AC=4,CD=.
∴AD==.
【点睛】本题主要考查直角三角形、全等三角形的判定与性质以及与圆有关的位置关系 .
7.(1)见解析
(2)1
【分析】(1)根据切线判定定理可得,先证四边形ODCE是矩形,再根据正方形的判定即可求证;
(2)设的半径为r,根据正方形的性质可得,从而得到,,再由切线长定理可得,,然后根据,即可求解.
【详解】(1)证明:∵BC,AC分别切于点D,E,
∴,,
又∵,
∴四边形ODCE是矩形,
又∵,
∴矩形ODCE是正方形.
(2)解:设的半径为r,
∵四边形ODCE是正方形,
∴,
在中,,
∴,,
∵与各边相切于点D,E,F,
∴,,
又∵,
∴,解得
∴内切圆的半径是1.
【点睛】本题主要考查了切线长定理,矩形的判定,正方形的判定和性质,勾股定理,熟练掌握切线长定理,正方形的判定和性质,勾股定理是解题的关键.
8.(1)r=3cm. (2) r=(a+b-c).
【分析】首先设AC、AB、BC与⊙O的切点分别为D、E、F;易证得四边形OFCD是正方形;那么根据切线长定理可得: CD=CF=(AC+BC-AB),由此可求出r的长.
【详解】(1)如图,连接OD,OF;
在Rt△ABC中,∠C=90°,AC=12cm,BC=9cm;
根据勾股定理AB==15cm;
四边形OFCD中,OD=OF,∠ODC=∠OFC=∠C=90°;
则四边形OFCD是正方形;由切线长定理,得:AD=AE,CD=CF,BE=BF;
则CD=CF=(AC+BC-AB);
即:r=(12+9-15)=3cm.
(2)当AC=b,BC=a,AB=c,由以上可得: CD=CF=(AC+BC-AB);
即:r=(a+b-c).则⊙O的半径r为:(a+b-c).
【点睛】此题主要考查直角三角形内切圆的性质及半径的求法.利用切线长定理得出四边形OFCD是正方形是解题关键.
9.(1)AB+CD=AD+BC,证明详见解析;(2)4m.
【分析】(1)由切线长定理,得:AM=AH,BN=BM,CN=CG,DG=DH,所以AB+CD=AD+BC,
(2)AD∥BC,在梯形ABCD中,由梯形的中位线定理得,AD+BC=2m,梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m
【详解】(1)AB+CD=AD+BC
证明:由切线长定理,得:AM=AH,BN=BM,CN=CG,DG=DH,
所以AB+CD=AM+BM+CG+DG=AH+BN+CN+DH=AD+BC,
即AB+CD=AD+BC
(2)AD∥BC,在梯形ABCD中,由梯形的中位线定理得,
AD+BC=2m,
梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m
【点睛】考查了圆外切四边形的性质:圆外切四边形的两组对边和相等;也考查了梯形的中位线定理,梯形的中位线平行于两底,并且等于两底和的一半 .
10.见解析.
【分析】由切线长定理可得AD+BC=AB+CD=2AB,根据梯形中位线定理可得AD+BC=2EF,进而可得EF=AB.
【详解】∵等腰梯形ABCD是的外切等腰梯形,
∴AD+BC=AB+CD=2AB,
∵梯形中位线为EF,
∴AD+BC=2EF,
∴EF=AB.
【点睛】本题考查切线长定理及梯形的中位线,从圆外一点引圆的两条切线,它们的长相等,这一点和圆心的连线平分两条切线的夹角;熟知圆外切四边形对边和相等是解题关键.
11.(1)见解析
(2)AI=4
【分析】(1)欲证明EB=EI,只要证明∠EBI=∠EIB;
(2)连接EC,过点E作EM⊥AB,EN⊥AC交AC的延长线于N,证明△AEM≌△AEN和△BME≌△CNE,再利用勾股定理计算即可解决问题.
【详解】(1)证明:∵I是△ABC的内心,
∴AE平分∠CAB,BI平分∠ABC,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠BIE=∠BAE+∠ABI,∠IBE=∠IBD+∠EBD,
∵∠CBE=∠CAE,
∴∠BIE=∠EBI,
∴EB=EI;
(2)解:连接EC,过点E作EM⊥AB,EN⊥AC交AC的延长线于N,则EM=EN,
∵∠BAE=∠CAE,
∴=,
∴BE=EC=4.
∵AE=AE,EM=EN,
∴△AEM≌△AEN,
∴AM=AN.
∵BE=EC,EM=EN,
△BME≌△CNE(HL),
∴BM=CN.
设BM为x,则8-x=6+x,解得x=1,即BM=1,
∴AM=7.
又∵BE=4,由勾股定理得,EM==.
∴AE==8,
∵EI=BE=4,
∴AI=AE EI=4.
【点睛】本题考查的是三角形的内切圆与内心,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
12.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据三角形内心的定义得,再由圆周角与弧之间的关系即可得证;
(2)连接,证出即可得证;
(3)连接,,,证出即可得证.
【详解】(1)证明:点I是的内心,
平分,
,
,
,
.
(2)证明:如图,连接,
点I是的内心,
平分,平分,
,
又,
,
,,
,
.
(3)证明:如图,连接,,,
,
.
,
∴点D是的外心.
【点睛】本题考查了三角形内心和外心的定义,圆的基本性质中圆周角与弧之间的关系等,理解定义,掌握圆的基本性质,根据题意作出辅助线是解题的关键.
13.
【分析】设,根据切线长定理列出方程即可.
【详解】解:设,
根据切线长定理得:,
解得:,
∴.
【点睛】本题考查了切线长定理,三元一次方程组的应用,根据切线长定理列出方程组是解本题的关键.
14.(1)见解析
(2)见解析
(3)AE=2
【分析】(1)连接OC.证∠D=∠COB.由OD⊥AB,得∠COB+∠COD=90°.可证∠D+∠COD=90°.即∠DCO=90°;
(2)由∠DCE+∠ACO=90°,∠AEO+∠A=90°和∠A=∠ACO,∠DEC=∠AEO,可得∠DEC=∠DCE ,即DE=DC.
(3)先求得OC=4,AB=2OC=8, OE=OD-DE=2,再证△AOE∽△ACB,得.
【详解】(1)证明:连接OC,如图,
∵OA=OC,
∴∠ACO=∠A,
∴∠COB=∠A+∠ACO=2∠A,
又∵∠D=2∠A,
∴∠D=∠COB.
又∵OD⊥AB,
∴∠COB+∠COD=90°,
∴∠D+∠COD=90°,即∠DCO=90°,
∴OC⊥DC,
又点C在⊙O上,
∴CD是⊙O的切线;
(2)证明:∵∠DCO=90°,
∴∠DCE+∠ACO=90°,
又∵OD⊥AB,
∴∠AEO+∠A=90°,
又∵∠A=∠ACO,∠DEC=∠AEO,
∴∠DEC=∠DCE,
∴DE=DC;
(3)解:∵∠DCO=90°,OD=5,DC=3,
∴OC===4,
∴OA=OC=4,
又DE=DC=3,
∴OE=OD﹣DE=2,
在Rt△AEO中,由勾股定理得:,
∴AE=2.
【点睛】此题考查了切线判定,等腰三角形判定,相似三角形判定,勾股定理,解题的关键是根据所求分析出必要条件,根据相关判定和性质求出有关的角和边的长度.
15.(1)见解析;(2).
【分析】(1)先根据等腰三角形的性质可得∠BPA=∠BAP、∠OAC=∠OCA.再运用等量代换说明∠OAB=90°,即可证明结论;
(2)先由勾股定理可得OP=2, 设AB=x,则OB=x+2.在Rt△AOB中运用勾股定理列方程解答即可.
【详解】解:(1)证明:∵BA=BP,
∴∠BPA=∠BAP.
∵OA=OC,
∴∠OAC=∠OCA.
∵OP⊥OC,
∴∠COP=90°.
∴∠OPC+∠OCP=90°.
∵∠APB=∠OPC,
∴∠BAP+∠OAC=90°.即∠OAB=90°,
∴OA⊥AB.
∵OA为半径,
∴AB为⊙O的切线;
(2)在Rt△OPC中,OC=4,PC=,
∴OP=2.
设AB=x,则OB=x+2.
在Rt△AOB中,,
∴x=3,即AB=3.
【点睛】本题主要考查了圆的性质、圆的切线证明、勾股定理等知识点,灵活运用相关性质、定理成为解答本题的关键.
16.(1)见解析
(2)13
(3)
【分析】(1)连接,利用角平分线的性质,同圆的半径相等,等腰三角形的性质,平行线的判定与性质和圆的切线的判定定理解得即可.
(2)连接 ,过点 作 与点 ,利用切割线定理,垂径定理和矩形的判定与性质解答即可;
(3)连接 , , ,过 作 与点H,利用(2)的结论,等腰直角三角形的判定与性质,圆周角定理,勾股定理解答即可.
【详解】(1)证明:连接,如图
平方
与点D
为的⊙O半径
是⊙O切线
(2)解:连接 ,过点O作于点F,如图,
则
由(1)知,是⊙O的切线
,
由(1)知,
四边形是矩形
(3)解:连接,,,过 作 与点H,如图,
由(2)知:⊙O的半径为13,
为的⊙O直径
为 中点
为等腰直角三角形
【点睛】本题考查角平分线性质,圆周角定理,勾股定理,切割线定理,圆的切线定理以及平行线的判定,熟练掌握这些定理和性质并且画对辅助线是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
