2008年九年级(下)第一次联考数学试卷(安徽省安庆市怀宁县)
文档属性
| 名称 | 2008年九年级(下)第一次联考数学试卷(安徽省安庆市怀宁县) |

|
|
| 格式 | rar | ||
| 文件大小 | 81.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-23 00:00:00 | ||
图片预览


文档简介
怀宁县2008年九年级(下)第一次联考
数 学 试 卷
考生注意:1.数学试卷共8页,共24题.请您仔细核对每页试卷下方页码和题数,核实无误后再答题.
2.请您仔细思考、认真答题,不要过于紧张,祝考试顺利!
题号 一 二 三 总分
(1~10) (11~16) 17 18 19 20 21 22 23 24
得分
一、选择题:(本大题共10小题,每小题4分,共40分.)在每小题给出的四个选项中,只有一项是符合题意的,请把你认为正确的选项前字母填写在该题后面的括号中.
1.下列计算正确的是 ( )
(A)2a2·a3=2a6 (B)(3a2)3=9a6 (C)a6÷a2=a3 (D)(a-2)3=a-6
2.抛物线y=-(a-8)2+2的顶点坐标是 ( )
(A)(2,8) (B)(8,2) (C)(—8,2) (D)(—8,—2)
3.已知圆锥的底面半径为9㎝,母线长为30㎝,则圆锥的侧面积为 ( )
(A)270πcm2 (B)360πcm2 (C)450πcm2 (D)540πcm2
4.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有 ( )
(A)1对 (B)2对
(C)3对 (D)4对
5.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张,妮妮2张,每张卡片大小、质地均匀相同,将画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到京京的概率是 ( )
(A) (B) (C) (D)
6.如果一个定值电阻R两端所加电压为5伏时,通过它的电流为1安培,那么通过这一电阻的电流I随它的两端电压U变化的图像是 ( )
(A) (B) (C) (D)
7.如图是5×5的正方形网络,以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出 ( )
(A)2个 (B)4个
(C)6个 (D)8个
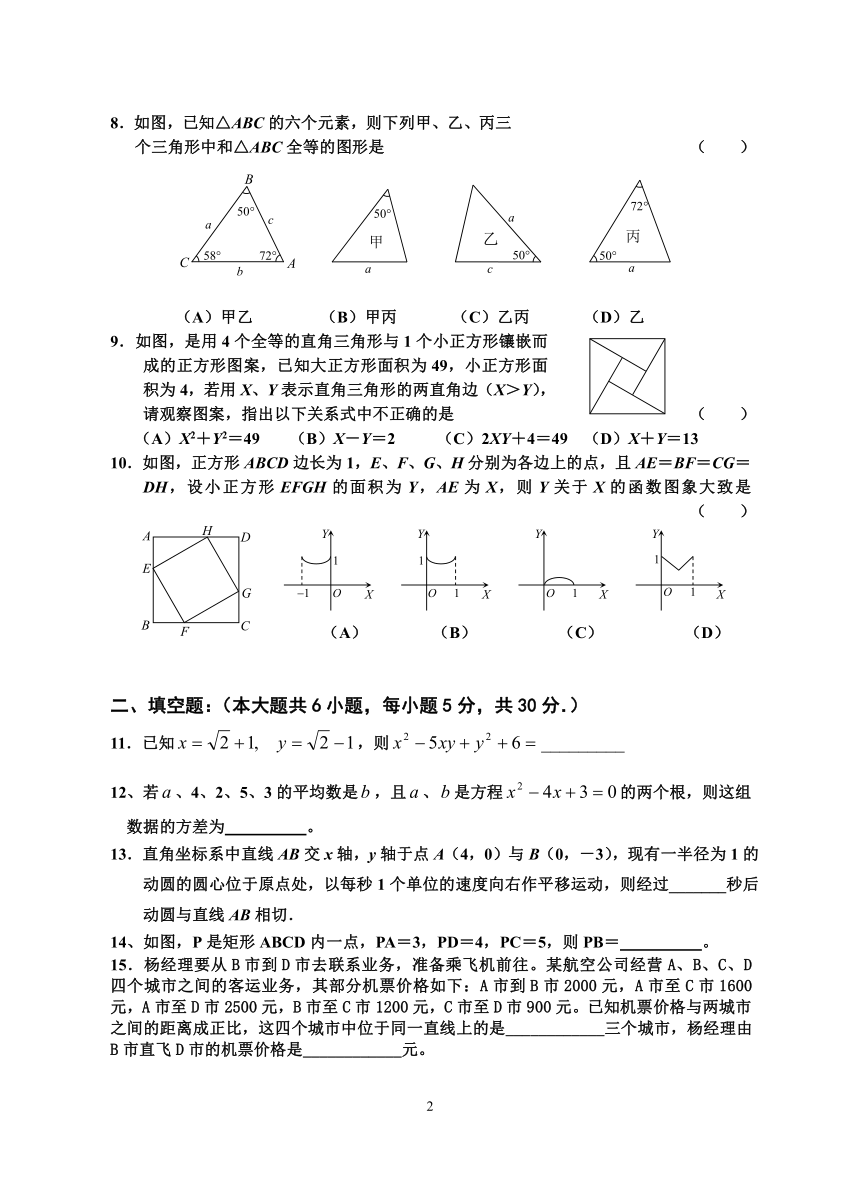
8.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是 ( )
(A)甲乙 (B)甲丙 (C)乙丙 (D)乙
9.如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用X、Y表示直角三角形的两直角边(X>Y),请观察图案,指出以下关系式中不正确的是 ( )
(A)X2+Y2=49 (B)X-Y=2 (C)2XY+4=49 (D)X+Y=13
10.如图,正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为Y,AE为X,则Y关于X的函数图象大致是 ( )
(A) (B) (C) (D)
二、填空题:(本大题共6小题,每小题5分,共30分.)
11.已知,则
12、若、4、2、5、3的平均数是,且、是方程的两个根,则这组数据的方差为 。
13.直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒1个单位的速度向右作平移运动,则经过_______秒后动圆与直线AB相切.
14、如图,P是矩形ABCD内一点,PA=3,PD=4,PC=5,则PB= 。
15.杨经理要从B市到D市去联系业务,准备乘飞机前往。某航空公司经营A、B、C、D四个城市之间的客运业务,其部分机票价格如下:A市到B市2000元,A市至C市1600元,A市至D市2500元,B市至C市1200元,C市至D市900元。已知机票价格与两城市之间的距离成正比,这四个城市中位于同一直线上的是____________三个城市,杨经理由B市直飞D市的机票价格是____________元。
16.小明设计了一个电子游戏:一电子跳蚤从横坐标为t(t>0)的P1点开始,按点的横坐标依次增加1的规律,在抛物线y=ax2(a>0)上向右跳动,得到点P2、P3,这时△P1P2P3的面积为_________.
三、解答题:(本大题共8小题,共80分.)解答应写明文字说明和运算步骤.
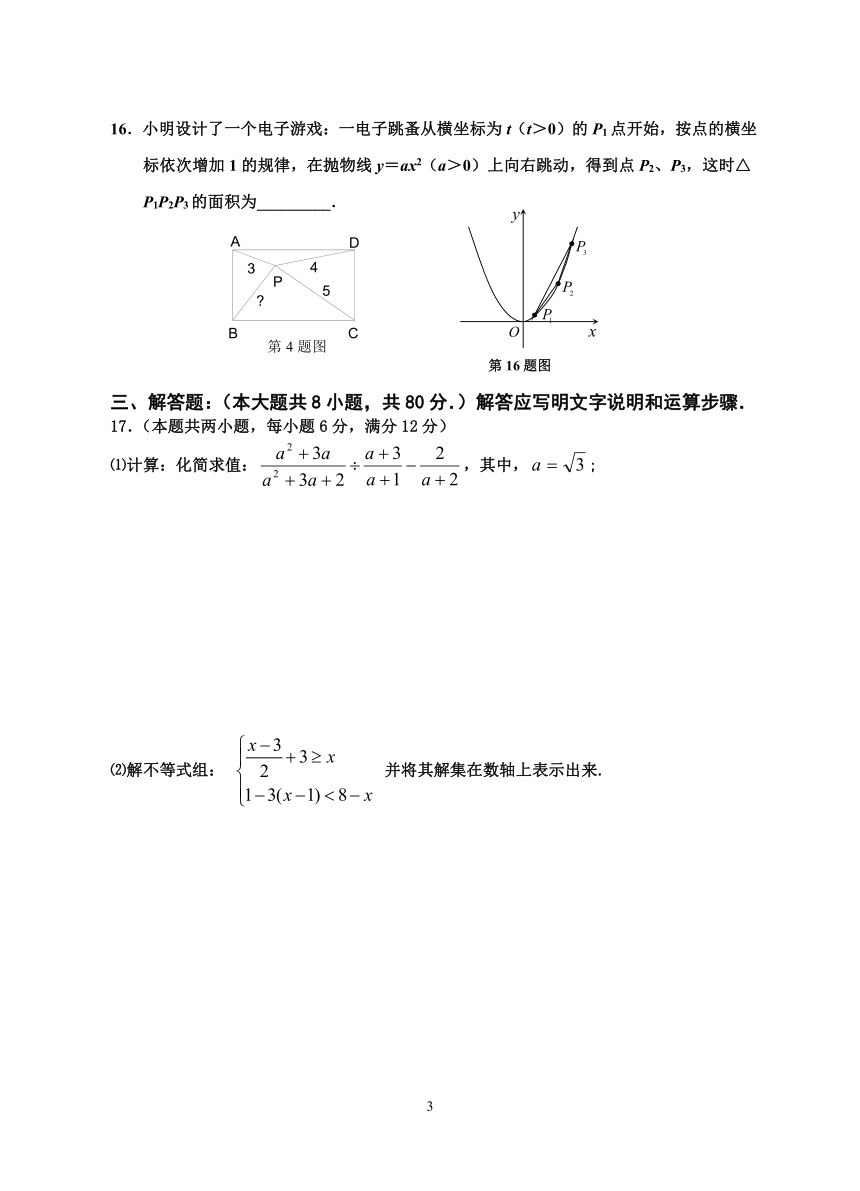
17.(本题共两小题,每小题6分,满分12分)
⑴计算:化简求值:,其中,;
⑵解不等式组: 并将其解集在数轴上表示出来.
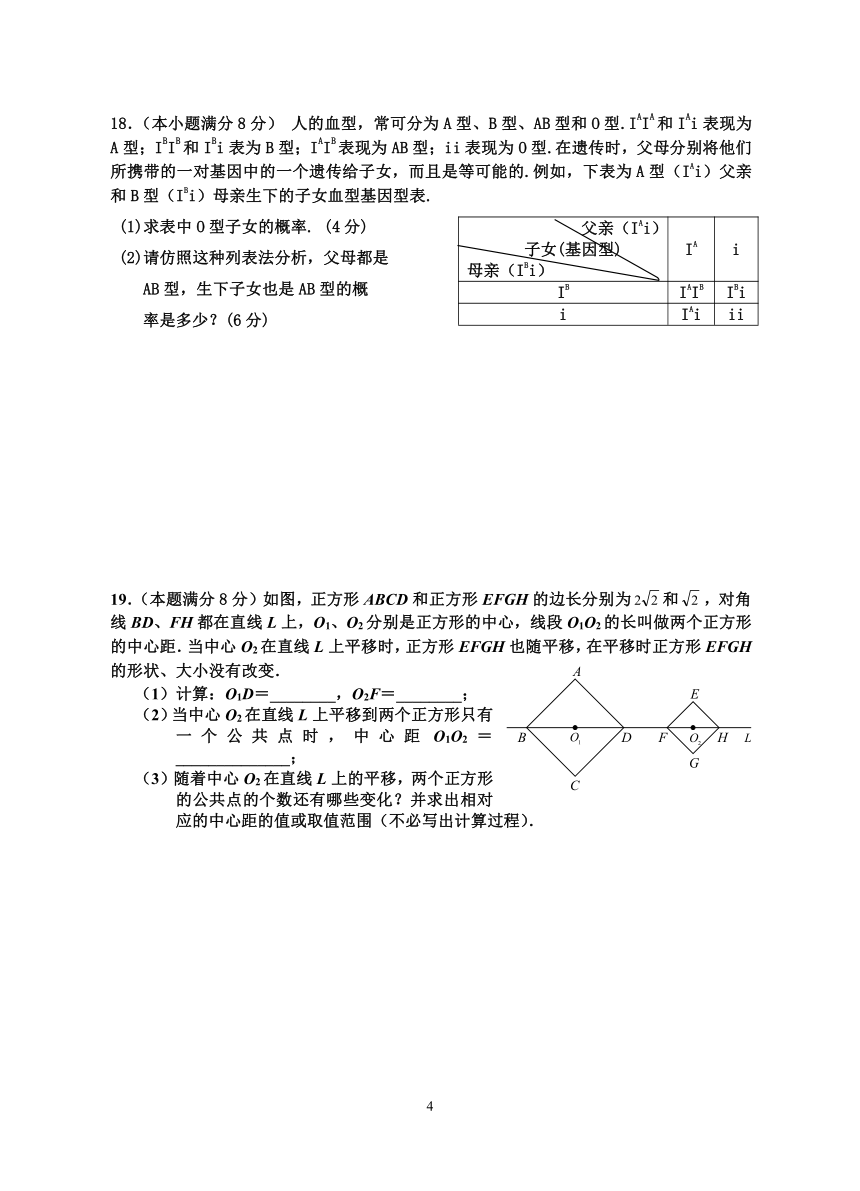
18.(本小题满分8分) 人的血型,常可分为A型、B型、AB型和O型.IAIA和IAi表现为A型;IBIB和IBi表为B型;IAIB表现为AB型;ii表现为O型.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如,下表为A型(IAi)父亲和B型(IBi)母亲生下的子女血型基因型表.
父亲(IAi)子女(基因型)母亲(IBi) IA i
IB IAIB IBi
i IAi ii
(1)求表中O型子女的概率. (4分)
(2)请仿照这种列表法分析,父母都是
AB型,生下子女也是AB型的概
率是多少?(6分)
19.(本题满分8分)如图,正方形ABCD和正方形EFGH的边长分别为和,对角线BD、FH都在直线L上,O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距.当中心O2在直线L上平移时,正方形EFGH也随平移,在平移时正方形EFGH的形状、大小没有改变.
(1)计算:O1D=________,O2F=________;
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2=______________;
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程).
20.(本小题满分8分)本商店积压了100件某种商品,为使这批货物尽快出售,该商店采取了如下销售方案,先将价格提高到原来的2.5倍,再作三次降价处理;第一次降价30%标出了“亏本价”,第二次降价30%,标出“破产价”,第三次又降价30%,标出“跳楼价”,三次降价处理销售情况如右表.
问:(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪一种方案更盈利,请通过计算加以说明.
21.(本小题满分10分)阅读并解答下面问题:
(1)如图所示,直线l的两侧有A、B两点,在l上求作一点P,使AP+BP的值最小(要求尺规作图,保留作图痕迹,不写画法和证明)
(2)如图A、B两个化工厂位于一段直线形河堤的同侧,A工厂至河堤的距离AC为1km,B工厂到河堤的距离BD为2km,经测量河堤上C、D两地间的距离为6km.现准备在河堤边修建一个污水处理厂,为使A、B两厂到污水处理厂的排污管道最短,污水处理厂应建在距C地多远的地方?
(3)通过以上解答,充分展开联想,运用数形结合思想,请你尝试解决下面问题:若,当为何值时,的值最小,并求出这个最小值。
22.(本小题满分10分)据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度V(km/h)与时间t(h)的函数图象如图所示,过线段OA上一点T(t,0)作横轴的垂线L,梯形OABC在直线L左侧部分的面积即为t(h)内沙尘暴所经过的路程S(km).
(1)当t=4时,求S的值;
(2)将S随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
23.(本小题满分12分)
如图,点A在Y轴上,点B在X轴上,且OA=OB=1,经过原点O的直线L交线段AB于点C,过C作OC的垂线,与直线X=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(1)当△AOC和△BCP全等时,求出t的值.
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论.
(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围;②求出当△PBC为等腰三角形时点P的坐标.
24、(本小题满分12分)如图,⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在弧CB上取一点D,分别作直线CD,ED交直线AB于F,M,连结OC,MC.
求∠AOC和∠MDF的度数;
求证:△MDF∽△MOC.
怀宁县2008年九年级(下)第一次联考数学试卷参考答案
一、选择题:(本大题共10小题,每小题4分,共40分.)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A C C D B C D B
二、填空题(本大题共6小题,每小题5分,共30分.)
11.7 12. 2 13. 14. 15. A、C、D 1500; 16.a
三、解答题
17.(1) 解:原式=…………………………1分
=………………………2分
=…………………………………………3分
=……………………………………………………4分
当时,原式=…………………………5分
=。………………………………………………………6分
⑵解:解不等式得x≥3;……………………………………2 分
解不等式 1-3 (x-1) < 8-x,得x>-2.……………………………………… 4 分
所以,原不等式组的解集是-2 < x≤3.…………………………………… 5 分
在数轴上表示为
18. (1)P(O型子女)
父亲(IAIB)子女(基因型)母亲( IAIB ) IA IB
IA IAIA IAIB
IB IAIB IBIB
(2)
19.(1)O1D=2 O2F=1 (2分) (2)O1O2=3 (4分)
(3)两个公共点 1<O1O2<3 (5分)
无数个公共点 O1O2=1 (6分)
1个公共点 O1O2=3 (7分)
无公共点 O1O2>3或0≤O1O2<1 (8分)
20.设原价为1
(1)亏本价=1×2.5(1-30%)=1.75 (1分)
破产价=1.75(1-30%)=1.225 (2分)
跳楼价=1.225(1-30%)=0.8575
跳楼价占原价的百分比为85.75% (4分)
(2)原价销售额:100×1=100 (5分)
实际销售额:10×1.75+40×1.225+50×0.8575=109.375 (7分)
∴按新销售方案销售更盈利. (8分)
21.(10分)解:(1)
………………………………2分
(2)由(1)知:A 与A关于CD对称,点P为污水处理厂的位置,
由题知:AC=1,BD=2,CD=6,设PC=x,
由△A CP∽△BDP得,…………………………………………………4分
∴,解得x=2,
∴污水处理厂应建在距C地2km的河堤边。……………………………………6分
(3)设AC=1,BD=2,CD=9,PC=x,
则PA = , PB=,……………………………………………7分
由(2)知,当A ,P,B共线时,PA + PB=y最小,……………………………8分
这时,,解得x=3,
当x=3时,y=+值最小,………………………………9分
最小值为。…………………………………………………………………10分
22.(1)UOA=3t S= (3分)
(2)S1=(0≤t≤10) S2=30t-150 (10<t≤20)
S3=-t2+70t-550(20<t≤35) (7分)
(3)S1=≤t≤10)最大值为150≤650 S2=30t-150=650 ∴t=>20不可能
S3=- ∴t1=30,t2=40,∵20<t≤35 ∴t=30 (10分)
23.(1)t= (3分) (2)OC=CP (4分)
过点C作X轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可(7分)
(3)①(0≤t≤1) (10分)
②当t=0或1时,△PBC为等腰三角形,即P(1.1), P(1,1-) (12分 )
24.(1).解:如图,连结OE,在Rt△OCG中,
∴∠OCG=30°.
∴∠AOC=60°.
∵AB为⊙O的直径, CE⊥AB,
∴∠EOC=2∠AOC=120°.
∴∠CDE=60°.
∴∠MDF=120°.
(2)证明:易证△CMG≌△EMG(SSS), ∴∠CMG=∠EMG.而∠DMF=∠EMG.
∴∠CMG=∠DMG.
又∵∠COM=∠FDM=120°,
∴△COM∽△FDM.
t(h)
V(km/h)
降价次数 一 二 三
销售件数 10 40 一抢而光
B
C
D
F
E
U(V)
I(A)
U(V)
I(A)
G O M
A
B
C
D
F
E
C D
G O M
A
第16题图
B
A
B.
A.
U(V)
I(A)
U(V)
I(A)
PAGE
6
数 学 试 卷
考生注意:1.数学试卷共8页,共24题.请您仔细核对每页试卷下方页码和题数,核实无误后再答题.
2.请您仔细思考、认真答题,不要过于紧张,祝考试顺利!
题号 一 二 三 总分
(1~10) (11~16) 17 18 19 20 21 22 23 24
得分
一、选择题:(本大题共10小题,每小题4分,共40分.)在每小题给出的四个选项中,只有一项是符合题意的,请把你认为正确的选项前字母填写在该题后面的括号中.
1.下列计算正确的是 ( )
(A)2a2·a3=2a6 (B)(3a2)3=9a6 (C)a6÷a2=a3 (D)(a-2)3=a-6
2.抛物线y=-(a-8)2+2的顶点坐标是 ( )
(A)(2,8) (B)(8,2) (C)(—8,2) (D)(—8,—2)
3.已知圆锥的底面半径为9㎝,母线长为30㎝,则圆锥的侧面积为 ( )
(A)270πcm2 (B)360πcm2 (C)450πcm2 (D)540πcm2
4.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有 ( )
(A)1对 (B)2对
(C)3对 (D)4对
5.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张,妮妮2张,每张卡片大小、质地均匀相同,将画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到京京的概率是 ( )
(A) (B) (C) (D)
6.如果一个定值电阻R两端所加电压为5伏时,通过它的电流为1安培,那么通过这一电阻的电流I随它的两端电压U变化的图像是 ( )
(A) (B) (C) (D)
7.如图是5×5的正方形网络,以点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出 ( )
(A)2个 (B)4个
(C)6个 (D)8个
8.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是 ( )
(A)甲乙 (B)甲丙 (C)乙丙 (D)乙
9.如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用X、Y表示直角三角形的两直角边(X>Y),请观察图案,指出以下关系式中不正确的是 ( )
(A)X2+Y2=49 (B)X-Y=2 (C)2XY+4=49 (D)X+Y=13
10.如图,正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为Y,AE为X,则Y关于X的函数图象大致是 ( )
(A) (B) (C) (D)
二、填空题:(本大题共6小题,每小题5分,共30分.)
11.已知,则
12、若、4、2、5、3的平均数是,且、是方程的两个根,则这组数据的方差为 。
13.直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒1个单位的速度向右作平移运动,则经过_______秒后动圆与直线AB相切.
14、如图,P是矩形ABCD内一点,PA=3,PD=4,PC=5,则PB= 。
15.杨经理要从B市到D市去联系业务,准备乘飞机前往。某航空公司经营A、B、C、D四个城市之间的客运业务,其部分机票价格如下:A市到B市2000元,A市至C市1600元,A市至D市2500元,B市至C市1200元,C市至D市900元。已知机票价格与两城市之间的距离成正比,这四个城市中位于同一直线上的是____________三个城市,杨经理由B市直飞D市的机票价格是____________元。
16.小明设计了一个电子游戏:一电子跳蚤从横坐标为t(t>0)的P1点开始,按点的横坐标依次增加1的规律,在抛物线y=ax2(a>0)上向右跳动,得到点P2、P3,这时△P1P2P3的面积为_________.
三、解答题:(本大题共8小题,共80分.)解答应写明文字说明和运算步骤.
17.(本题共两小题,每小题6分,满分12分)
⑴计算:化简求值:,其中,;
⑵解不等式组: 并将其解集在数轴上表示出来.
18.(本小题满分8分) 人的血型,常可分为A型、B型、AB型和O型.IAIA和IAi表现为A型;IBIB和IBi表为B型;IAIB表现为AB型;ii表现为O型.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如,下表为A型(IAi)父亲和B型(IBi)母亲生下的子女血型基因型表.
父亲(IAi)子女(基因型)母亲(IBi) IA i
IB IAIB IBi
i IAi ii
(1)求表中O型子女的概率. (4分)
(2)请仿照这种列表法分析,父母都是
AB型,生下子女也是AB型的概
率是多少?(6分)
19.(本题满分8分)如图,正方形ABCD和正方形EFGH的边长分别为和,对角线BD、FH都在直线L上,O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距.当中心O2在直线L上平移时,正方形EFGH也随平移,在平移时正方形EFGH的形状、大小没有改变.
(1)计算:O1D=________,O2F=________;
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2=______________;
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程).
20.(本小题满分8分)本商店积压了100件某种商品,为使这批货物尽快出售,该商店采取了如下销售方案,先将价格提高到原来的2.5倍,再作三次降价处理;第一次降价30%标出了“亏本价”,第二次降价30%,标出“破产价”,第三次又降价30%,标出“跳楼价”,三次降价处理销售情况如右表.
问:(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪一种方案更盈利,请通过计算加以说明.
21.(本小题满分10分)阅读并解答下面问题:
(1)如图所示,直线l的两侧有A、B两点,在l上求作一点P,使AP+BP的值最小(要求尺规作图,保留作图痕迹,不写画法和证明)
(2)如图A、B两个化工厂位于一段直线形河堤的同侧,A工厂至河堤的距离AC为1km,B工厂到河堤的距离BD为2km,经测量河堤上C、D两地间的距离为6km.现准备在河堤边修建一个污水处理厂,为使A、B两厂到污水处理厂的排污管道最短,污水处理厂应建在距C地多远的地方?
(3)通过以上解答,充分展开联想,运用数形结合思想,请你尝试解决下面问题:若,当为何值时,的值最小,并求出这个最小值。
22.(本小题满分10分)据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度V(km/h)与时间t(h)的函数图象如图所示,过线段OA上一点T(t,0)作横轴的垂线L,梯形OABC在直线L左侧部分的面积即为t(h)内沙尘暴所经过的路程S(km).
(1)当t=4时,求S的值;
(2)将S随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
23.(本小题满分12分)
如图,点A在Y轴上,点B在X轴上,且OA=OB=1,经过原点O的直线L交线段AB于点C,过C作OC的垂线,与直线X=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(1)当△AOC和△BCP全等时,求出t的值.
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论.
(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围;②求出当△PBC为等腰三角形时点P的坐标.
24、(本小题满分12分)如图,⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在弧CB上取一点D,分别作直线CD,ED交直线AB于F,M,连结OC,MC.
求∠AOC和∠MDF的度数;
求证:△MDF∽△MOC.
怀宁县2008年九年级(下)第一次联考数学试卷参考答案
一、选择题:(本大题共10小题,每小题4分,共40分.)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A C C D B C D B
二、填空题(本大题共6小题,每小题5分,共30分.)
11.7 12. 2 13. 14. 15. A、C、D 1500; 16.a
三、解答题
17.(1) 解:原式=…………………………1分
=………………………2分
=…………………………………………3分
=……………………………………………………4分
当时,原式=…………………………5分
=。………………………………………………………6分
⑵解:解不等式得x≥3;……………………………………2 分
解不等式 1-3 (x-1) < 8-x,得x>-2.……………………………………… 4 分
所以,原不等式组的解集是-2 < x≤3.…………………………………… 5 分
在数轴上表示为
18. (1)P(O型子女)
父亲(IAIB)子女(基因型)母亲( IAIB ) IA IB
IA IAIA IAIB
IB IAIB IBIB
(2)
19.(1)O1D=2 O2F=1 (2分) (2)O1O2=3 (4分)
(3)两个公共点 1<O1O2<3 (5分)
无数个公共点 O1O2=1 (6分)
1个公共点 O1O2=3 (7分)
无公共点 O1O2>3或0≤O1O2<1 (8分)
20.设原价为1
(1)亏本价=1×2.5(1-30%)=1.75 (1分)
破产价=1.75(1-30%)=1.225 (2分)
跳楼价=1.225(1-30%)=0.8575
跳楼价占原价的百分比为85.75% (4分)
(2)原价销售额:100×1=100 (5分)
实际销售额:10×1.75+40×1.225+50×0.8575=109.375 (7分)
∴按新销售方案销售更盈利. (8分)
21.(10分)解:(1)
………………………………2分
(2)由(1)知:A 与A关于CD对称,点P为污水处理厂的位置,
由题知:AC=1,BD=2,CD=6,设PC=x,
由△A CP∽△BDP得,…………………………………………………4分
∴,解得x=2,
∴污水处理厂应建在距C地2km的河堤边。……………………………………6分
(3)设AC=1,BD=2,CD=9,PC=x,
则PA = , PB=,……………………………………………7分
由(2)知,当A ,P,B共线时,PA + PB=y最小,……………………………8分
这时,,解得x=3,
当x=3时,y=+值最小,………………………………9分
最小值为。…………………………………………………………………10分
22.(1)UOA=3t S= (3分)
(2)S1=(0≤t≤10) S2=30t-150 (10<t≤20)
S3=-t2+70t-550(20<t≤35) (7分)
(3)S1=≤t≤10)最大值为150≤650 S2=30t-150=650 ∴t=>20不可能
S3=- ∴t1=30,t2=40,∵20<t≤35 ∴t=30 (10分)
23.(1)t= (3分) (2)OC=CP (4分)
过点C作X轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可(7分)
(3)①(0≤t≤1) (10分)
②当t=0或1时,△PBC为等腰三角形,即P(1.1), P(1,1-) (12分 )
24.(1).解:如图,连结OE,在Rt△OCG中,
∴∠OCG=30°.
∴∠AOC=60°.
∵AB为⊙O的直径, CE⊥AB,
∴∠EOC=2∠AOC=120°.
∴∠CDE=60°.
∴∠MDF=120°.
(2)证明:易证△CMG≌△EMG(SSS), ∴∠CMG=∠EMG.而∠DMF=∠EMG.
∴∠CMG=∠DMG.
又∵∠COM=∠FDM=120°,
∴△COM∽△FDM.
t(h)
V(km/h)
降价次数 一 二 三
销售件数 10 40 一抢而光
B
C
D
F
E
U(V)
I(A)
U(V)
I(A)
G O M
A
B
C
D
F
E
C D
G O M
A
第16题图
B
A
B.
A.
U(V)
I(A)
U(V)
I(A)
PAGE
6
