人教版五年级上册数学6.3梯形的面积课件(共19张PPT)
文档属性
| 名称 | 人教版五年级上册数学6.3梯形的面积课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 04:53:47 | ||
图片预览



文档简介
(共19张PPT)
6 多边形的面积
第3讲 梯形的面积
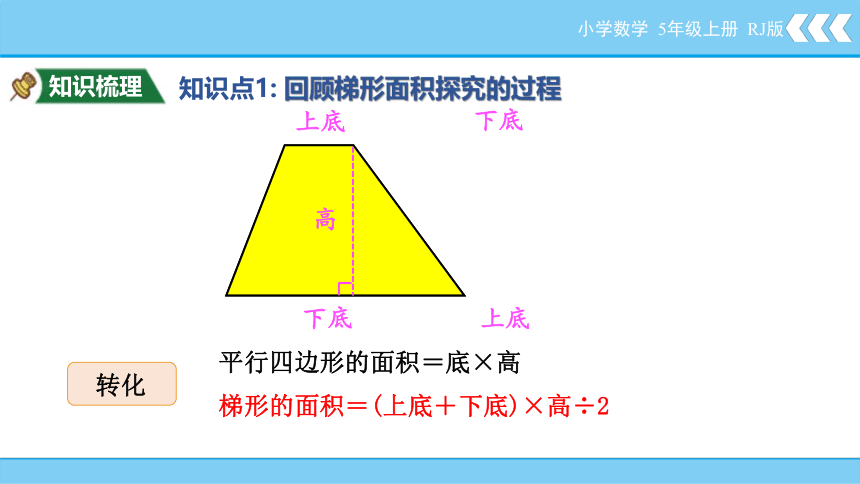
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
转化
平行四边形的面积=底×高
梯形的面积=(上底+下底)×高÷2
上底
下底
高
上底
下底
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是:
b
a
h
S=(a+b)h÷2
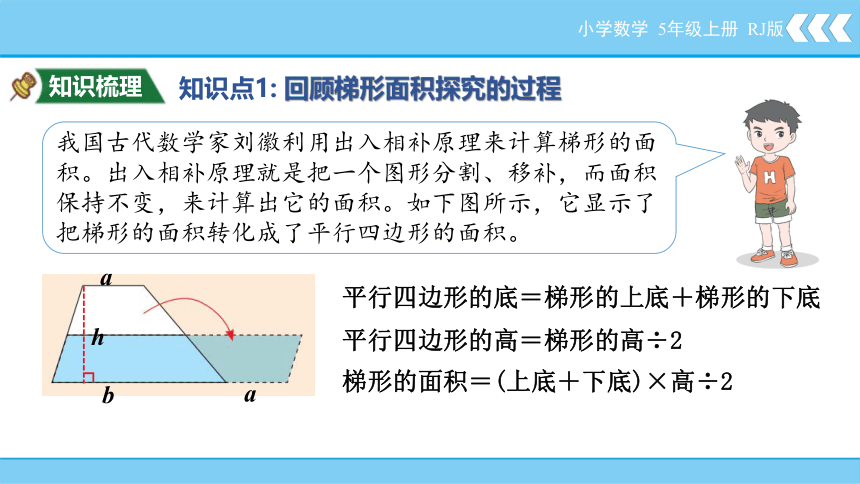
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
我国古代数学家刘徽利用出入相补原理来计算梯形的面积。出入相补原理就是把一个图形分割、移补,而面积保持不变,来计算出它的面积。如下图所示,它显示了把梯形的面积转化成了平行四边形的面积。
h
a
a
b
平行四边形的底=梯形的上底+梯形的下底
平行四边形的高=梯形的高÷2
梯形的面积=(上底+下底)×高÷2
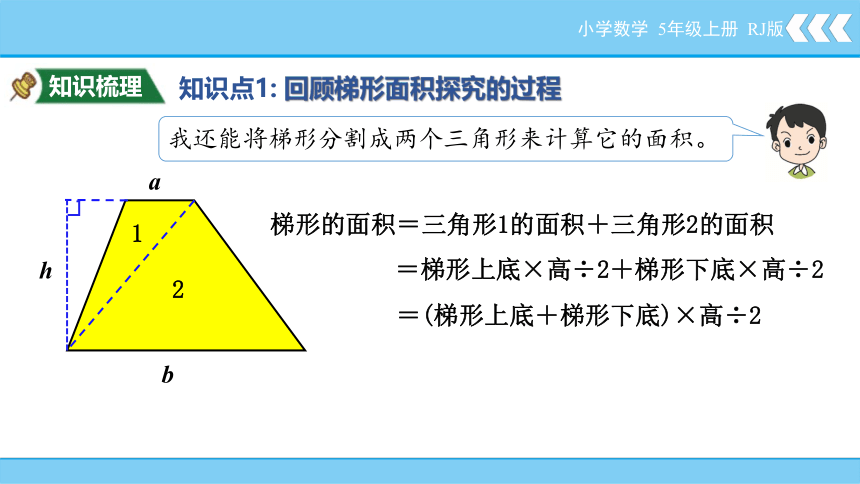
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
1
2
我还能将梯形分割成两个三角形来计算它的面积。
梯形的面积=三角形1的面积+三角形2的面积
=梯形上底×高÷2+梯形下底×高÷2
=(梯形上底+梯形下底)×高÷2
a
b
h
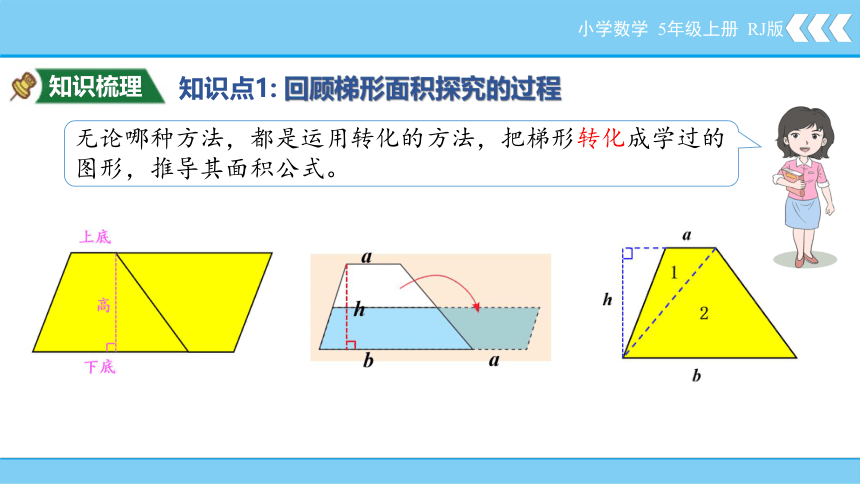
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
无论哪种方法,都是运用转化的方法,把梯形转化成学过的图形,推导其面积公式。
知识梳理
知识点2: 运用公式解决实际问题
小学数学 5年级上册 RJ版
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m )
答:它的面积是10530 m 。
知识梳理
知识点2: 运用公式解决实际问题
小学数学 5年级上册 RJ版
(顶层根数+底层根数)×层数÷2
10个
5层
=10×5÷2
=25(个)
(顶层根数+底层根数)×层数÷2
易错点睛
小学数学 5年级上册 RJ版
1.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
易错点睛
小学数学 5年级上册 RJ版
1.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
16-9=7(cm)
7
S=(a+b)h÷2
=(7+16)×12÷2
=138(cm2)
上底=8.6-1.6-2.8=4.2(cm)
S=(a+b)h÷2
=(4.2+8.6)×5.2÷2
=33.28(cm2)
4.2
易错点睛
小学数学 5年级上册 RJ版
★易错提示:利用隐含信息找到上底、下底和高。
3.5
上底=6-2.5=3.5(cm)
S=(a+b)h÷2
=(3.5+6)×3.5÷2
=16.625(cm2)
S=(a+b)h÷2
=(4+4+6)×4÷2
=28(cm2)
4
1.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
易错点睛
小学数学 5年级上册 RJ版
★易错提示:合理地运用梯形的面积公式解决问题。
2.一块“众志成城,抗击疫情”宣传牌的形状是梯形,上底是1.4 m,比下底短0.2 m,高是3.2 m。如果要在这块宣传牌的两面涂上油漆,每平方米用油漆0.8 kg,一共需要多少千克油漆?
下底=1.4+0.2=1.6(m)
S=(a+b)h÷2
=(1.4+1.6)×3.2÷2
=4.8(m2)
宣传牌两面的面积也就是两个梯形的面积之和。
答:一共需要7.68 kg油漆。
4.8+4.8=9.6(m )
9.6×0.8=7.68(kg)
1.计算下面图形的面积。
分层练习
(基础练习)
小学数学 5年级上册 RJ版
S =(a+b)h÷2
=(6+18)×8÷2
=96(cm2)
S=(a+b)h÷2
=(5.2+6.6)×5.8÷2
=34.22(dm2)
只要知道了梯形的上底、下底和高,可以直接运用梯形的面积计算公式计算。S=(a+b)h÷2。
分层练习
2.如图,汽车的前挡风玻璃近似是一个梯形。这块玻璃的面积是多少 平方厘米?(单位:cm)
小学数学 5年级上册 RJ版
(基础练习)
S=(a+b)h÷2
=(100+132)×55÷2
=6380(cm2)
答:这块玻璃的面积是6380 cm2。
合理地运用公式能帮我们解决生活中的很多实际问题。
分层练习
(提升练习)
1.如图,一块梯形菜地一面靠墙,围菜地的篱笆总长28 m,其中有一条篱笆边长为10 m。求这块菜地的面积。
小学数学 5年级上册 RJ版
S=(a+b)h÷2
=18×10÷2
=90(m )
?
篱笆总长=上底+下底+高
上底+下底=28-10=18(m)
答:这块菜地的面积是90 m 。
分层练习
(提升练习)
2.
一个梯形,上底是5 cm,下底是8 cm。如果把它的上底增加4 cm,面积就增加12 cm2。原梯形的面积是多少平方厘米?
h=2S÷a
=2×12÷4
=6(cm)
答:原梯形的面积是39 cm 。
小学数学 5年级上册 RJ版
4 cm
5 cm
8 cm
?cm
S=(a+b)h÷2
=(5+8)×6÷2
=39(cm )
1.如图,梯形ABCD和梯形EFGH是两个完全相同的梯形,把它们的一部分重叠在一起。求阴影部分的面积。(单位:cm)
分层练习
(拓展练习)
解题关键是把不规则的图形③的面积转化为规则的图形①的面积。
小学数学 5年级上册 RJ版
①
②
③
图形①的面积+图形②的面积=梯形EFGH的面积
图形③的面积+图形②的面积=梯形ABCD的面积
图形③的面积=图形①的面积
上底:12-3=9(cm)
S=(a+b)h÷2
=(9+12)×6÷2
=63(cm2)
答:阴影部分的面积是63 cm2。
=图形③的面积
2.如图1、图2所示,梯形上底AB长4 cm,下底CD长9 cm,高为4 cm,P为CD边上任意一点,求阴影部分的面积。你认为小明的想法怎么样?写出你这样判断的理由。
分层练习
(拓展练习)
小学数学 5年级上册 RJ版
=18(cm )
S阴=SABCD―S△ABP
=(4+9)×4÷2―4×4÷2
方法一:
2.如图1、图2所示,梯形上底AB长4 cm,下底CD长9 cm,高为4 cm,P为CD边上任意一点,求阴影部分的面积。你认为小明的想法怎么样?写出你这样判断的理由。
分层练习
(拓展练习)
小学数学 5年级上册 RJ版
解决这类问题的关键是利用已知图形的面积或面积公式求阴影部分的面积。
=(DP+PC)×4÷2
S阴=S△ADP +S△BPC
=DP×4÷2+PC×4÷2
方法二:
=9×4÷2
=18(cm )
答:阴影部分的面积是18 cm 。
6 多边形的面积
第3讲 梯形的面积
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
转化
平行四边形的面积=底×高
梯形的面积=(上底+下底)×高÷2
上底
下底
高
上底
下底
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是:
b
a
h
S=(a+b)h÷2
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
我国古代数学家刘徽利用出入相补原理来计算梯形的面积。出入相补原理就是把一个图形分割、移补,而面积保持不变,来计算出它的面积。如下图所示,它显示了把梯形的面积转化成了平行四边形的面积。
h
a
a
b
平行四边形的底=梯形的上底+梯形的下底
平行四边形的高=梯形的高÷2
梯形的面积=(上底+下底)×高÷2
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
1
2
我还能将梯形分割成两个三角形来计算它的面积。
梯形的面积=三角形1的面积+三角形2的面积
=梯形上底×高÷2+梯形下底×高÷2
=(梯形上底+梯形下底)×高÷2
a
b
h
知识梳理
知识点1: 回顾梯形面积探究的过程
小学数学 5年级上册 RJ版
无论哪种方法,都是运用转化的方法,把梯形转化成学过的图形,推导其面积公式。
知识梳理
知识点2: 运用公式解决实际问题
小学数学 5年级上册 RJ版
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m )
答:它的面积是10530 m 。
知识梳理
知识点2: 运用公式解决实际问题
小学数学 5年级上册 RJ版
(顶层根数+底层根数)×层数÷2
10个
5层
=10×5÷2
=25(个)
(顶层根数+底层根数)×层数÷2
易错点睛
小学数学 5年级上册 RJ版
1.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
易错点睛
小学数学 5年级上册 RJ版
1.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
16-9=7(cm)
7
S=(a+b)h÷2
=(7+16)×12÷2
=138(cm2)
上底=8.6-1.6-2.8=4.2(cm)
S=(a+b)h÷2
=(4.2+8.6)×5.2÷2
=33.28(cm2)
4.2
易错点睛
小学数学 5年级上册 RJ版
★易错提示:利用隐含信息找到上底、下底和高。
3.5
上底=6-2.5=3.5(cm)
S=(a+b)h÷2
=(3.5+6)×3.5÷2
=16.625(cm2)
S=(a+b)h÷2
=(4+4+6)×4÷2
=28(cm2)
4
1.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
易错点睛
小学数学 5年级上册 RJ版
★易错提示:合理地运用梯形的面积公式解决问题。
2.一块“众志成城,抗击疫情”宣传牌的形状是梯形,上底是1.4 m,比下底短0.2 m,高是3.2 m。如果要在这块宣传牌的两面涂上油漆,每平方米用油漆0.8 kg,一共需要多少千克油漆?
下底=1.4+0.2=1.6(m)
S=(a+b)h÷2
=(1.4+1.6)×3.2÷2
=4.8(m2)
宣传牌两面的面积也就是两个梯形的面积之和。
答:一共需要7.68 kg油漆。
4.8+4.8=9.6(m )
9.6×0.8=7.68(kg)
1.计算下面图形的面积。
分层练习
(基础练习)
小学数学 5年级上册 RJ版
S =(a+b)h÷2
=(6+18)×8÷2
=96(cm2)
S=(a+b)h÷2
=(5.2+6.6)×5.8÷2
=34.22(dm2)
只要知道了梯形的上底、下底和高,可以直接运用梯形的面积计算公式计算。S=(a+b)h÷2。
分层练习
2.如图,汽车的前挡风玻璃近似是一个梯形。这块玻璃的面积是多少 平方厘米?(单位:cm)
小学数学 5年级上册 RJ版
(基础练习)
S=(a+b)h÷2
=(100+132)×55÷2
=6380(cm2)
答:这块玻璃的面积是6380 cm2。
合理地运用公式能帮我们解决生活中的很多实际问题。
分层练习
(提升练习)
1.如图,一块梯形菜地一面靠墙,围菜地的篱笆总长28 m,其中有一条篱笆边长为10 m。求这块菜地的面积。
小学数学 5年级上册 RJ版
S=(a+b)h÷2
=18×10÷2
=90(m )
?
篱笆总长=上底+下底+高
上底+下底=28-10=18(m)
答:这块菜地的面积是90 m 。
分层练习
(提升练习)
2.
一个梯形,上底是5 cm,下底是8 cm。如果把它的上底增加4 cm,面积就增加12 cm2。原梯形的面积是多少平方厘米?
h=2S÷a
=2×12÷4
=6(cm)
答:原梯形的面积是39 cm 。
小学数学 5年级上册 RJ版
4 cm
5 cm
8 cm
?cm
S=(a+b)h÷2
=(5+8)×6÷2
=39(cm )
1.如图,梯形ABCD和梯形EFGH是两个完全相同的梯形,把它们的一部分重叠在一起。求阴影部分的面积。(单位:cm)
分层练习
(拓展练习)
解题关键是把不规则的图形③的面积转化为规则的图形①的面积。
小学数学 5年级上册 RJ版
①
②
③
图形①的面积+图形②的面积=梯形EFGH的面积
图形③的面积+图形②的面积=梯形ABCD的面积
图形③的面积=图形①的面积
上底:12-3=9(cm)
S=(a+b)h÷2
=(9+12)×6÷2
=63(cm2)
答:阴影部分的面积是63 cm2。
=图形③的面积
2.如图1、图2所示,梯形上底AB长4 cm,下底CD长9 cm,高为4 cm,P为CD边上任意一点,求阴影部分的面积。你认为小明的想法怎么样?写出你这样判断的理由。
分层练习
(拓展练习)
小学数学 5年级上册 RJ版
=18(cm )
S阴=SABCD―S△ABP
=(4+9)×4÷2―4×4÷2
方法一:
2.如图1、图2所示,梯形上底AB长4 cm,下底CD长9 cm,高为4 cm,P为CD边上任意一点,求阴影部分的面积。你认为小明的想法怎么样?写出你这样判断的理由。
分层练习
(拓展练习)
小学数学 5年级上册 RJ版
解决这类问题的关键是利用已知图形的面积或面积公式求阴影部分的面积。
=(DP+PC)×4÷2
S阴=S△ADP +S△BPC
=DP×4÷2+PC×4÷2
方法二:
=9×4÷2
=18(cm )
答:阴影部分的面积是18 cm 。
