1.5.1全称量词与存在量词 课件(共19张PPT)
文档属性
| 名称 | 1.5.1全称量词与存在量词 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 10:58:57 | ||
图片预览






文档简介
(共19张PPT)
第一章 集合与常用逻辑用语
1.5.1 全称量词与存在量词
素 养 目 标 学 科 素 养
1、通过已知的数学实例,理解全称量词与存在量词的意义,提升数学抽象素养.(重点) 2、掌握判断全称量词命题与存在量词命题真假的方法.(难点) 3、理解全称量词命题和存在量词命题与恒成立问题和存在性问题的关系(难点) 1.逻辑推理
2.数学抽象
教学目标
问题导入
阅读教材P26-27,回答问题
问题1 常见的全称量词、存在量词有哪些?
问题2 如何判断全称量词命题的真假?存在量词命题呢?
问题3 全称量词命题中一定会含有全称量词吗?存在量词命题呢?
全称量词
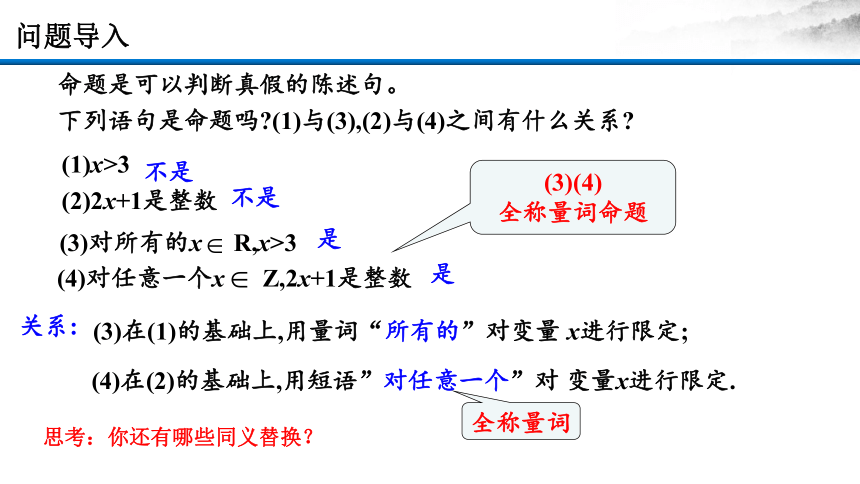
命题是可以判断真假的陈述句。
(1)x>3
(2)2x+1是整数
(3)对所有的x R,x>3
(4)对任意一个x Z,2x+1是整数
是
是
不是
不是
(3)在(1)的基础上,用量词“所有的”对变量 x进行限定;
关系:
(3)(4)
全称量词命题
(4)在(2)的基础上,用短语”对任意一个”对 变量x进行限定.
下列语句是命题吗 (1)与(3),(2)与(4)之间有什么关系
问题导入
思考:你还有哪些同义替换?
概念辨析
一.全称量词与全称量词命题
1.全称量词:短语“所有的”“任意一个”在逻辑中通常叫做 ____________,并用符号“______”表示.
2.全称量词命题:含有____________的命题,叫做全称量词命题.
3.全称量词命题的表述形式:全称量词命题
“对M中任意一个x,p(x)成立”,可用符号简记为__________________.
全称量词
全称量词
x∈M,p(x)
常见的全称量词还有“一切”“每一个”、“任给” 等
概念辨析
例1.判断下列全称量词命题的真假:
(1)所有的素数都是奇数;
(2);
(3)对任意一个无理数,也是无理数.
解:(1)2是素数,但2不是奇数.所以,全称量词命题“所有的素数都是奇数”是假命题.
(2),总有,因而.所以,全称量词命题“”是真命题.
(3)是无理数,但是有理数.所以,全称量词命题“对任意一个无理数,也是无理数”是假命题.
提示:如果一个大于1 的整数,除1和自身外无其他正因数,则称这个正整数为素数.
要判定全称量词命题“ ”是真命题,需要对集合M中每个元素x,证明 成立;如果在集合M集中找到一个元素x0,使 不成立,那么这个全称量词命题就是假命题.这个方法就是“举反例”.
概念辨析
概念辨析
变式练习1
判断1、2是否是全称量词命题,并尝试判断命题的真假
1、线段垂直平分线上的点到这条线段两个端点的距离相等
2、若x>1,则2x+1>5
3、“含有全称量词的命题”是“全称量词命题”的________条件
真
假
充分不必要
1和2都隐藏了全称量词,但它们是全称量词命题。
关系:
存在量词
下列语句是命题吗 (1)与(3),(2)与(4)之间有什么关系
(1)2x+1=3
(2)x能被2和3整除;
(3)存在一个x∈R,使2x+1=3;
(4)至少有一个x∈Z,x能被2和3整除.
(3)在(1)的基础上,用短语“存在一个”对变量x的取值进行限定,使(3)变成了可以判断真假的语句;
不是
不是
是
是
(4)在(2)的基础上,用“至少有一个”对变量x的取值进行限定,从而使 (4)变成了可以判断真假的语句.
(3)(4)
存在量词命题
概念辨析
概念辨析
二.存在量词与存在量词命题
1.存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做____________,并用符号“_____”表示.
2.存在量词命题:含有存在量词的命题,叫做________________.
3.存在量词命题的表述形式:存在量词命题
“存在M中的元素x,使p(x)成立”,可用符号简记为__________________.
存在量词
存在量词命题
x0∈M,p(x0)
常见的存在量词还有“有些
”“有一个”、“对有些” 等
概念辨析
问题4: 全称量词命题和存在量词命题中是否一定含有全称量词和特称量词?
全称量词命题不一定含有全称量词,比如全称量词命题“正方形是特殊的菱形”,其中没有全称量词。
问题5:短语“至多有一个”是存在量词吗
不是.因为“至多有一个”包含了不存在的情形.
举一些例子?
概念辨析
例2.判断下列存在量词命题的真假:
(1)有一个实数,使;
(2)平面内存在两条相交直线垂直于同一条直线;
(3)有些平行四边形是菱形.
解:(1)由于,因此一元二次方程无实根.所以,存在量词命题“有一个实数,使”是假命题.
(2)由于平面内垂直于同一条直线的两条直线互相平行,因此平面内不可能存在两条相交直线垂直于同一条直线.所以,存在量词命题“平面内存在两条相交直线垂直于同一条直线”是假命题.
(3)由于正方形既是平行四边形又是菱形,所以存在量词命题“有些平行四边形是菱形”是真命题.
要判定存在量词命题“ ”是真命题,需要在集合M中找到一个元素x,使得 成立;如果在集合M中使 成立的元素x不存在,那么这个存在量词命题就是假命题.
概念辨析
随堂练习
1、判断下列命题是全称量词命题还是存在量词命题.
(1)有些实数是无理数;
(2)每一个正方形都是平行四边形
(3)四边形的内角和是360°
(4) x∈R,x2+4x+4≤0;
(5) x∈R,x2+2<0;
(6)方程2x+1=0有整数解.
随堂练习
解:(1)“所有”是全称量词; x∈R,|x|+1>0.
(2)对所有实数a,b,方程ax+b=0恰有一个解;
解:(2)“所有”是全称量词; a,b∈R,方程ax+b=0恰有一个解.
2、指出下列命题中的全称量词或存在量词,并用量词符号“ ”或“ ”表示下列命题.
(1)所有实数x都能使|x|+1>0成立;
(3)存在整数x,y,使得3x-2y=10成立;
解:(3)“存在”是存在量词; x,y∈Z,3x-2y=10.
(4)存在实数m,使得m与m的倒数之和等于1.
随堂练习
随堂练习
(1)已知命题p: x∈{x|1≤x≤4}, x≥a, 若p为真命题,求实数a的取值范围
3、完成下列习题
(2)A={x|1≤x≤4}, x∈A,x-a≤0,求实数a的取值范围
让任意变成存在呢?
4.已知命题p: x∈{-1≤x≤3},x2-a-2≥0,若p为真命题,则实数a的取值范围为 .
{a|a≤-2}
解析:不等式x2-a-2≥0可化为a≤x2-2,
当x∈{-1≤x≤3}时,x2-2的最小值是-2,所以a≤-2.
随堂练习
课堂小结
1.理解全称量词与存在量词的意义
2.掌握判断全称量词命题与存在量词命题真假的方法
3、理解全称量词命题和存在量词命题与恒成立问题和存在性问题的关系
第一章 集合与常用逻辑用语
1.5.1 全称量词与存在量词
素 养 目 标 学 科 素 养
1、通过已知的数学实例,理解全称量词与存在量词的意义,提升数学抽象素养.(重点) 2、掌握判断全称量词命题与存在量词命题真假的方法.(难点) 3、理解全称量词命题和存在量词命题与恒成立问题和存在性问题的关系(难点) 1.逻辑推理
2.数学抽象
教学目标
问题导入
阅读教材P26-27,回答问题
问题1 常见的全称量词、存在量词有哪些?
问题2 如何判断全称量词命题的真假?存在量词命题呢?
问题3 全称量词命题中一定会含有全称量词吗?存在量词命题呢?
全称量词
命题是可以判断真假的陈述句。
(1)x>3
(2)2x+1是整数
(3)对所有的x R,x>3
(4)对任意一个x Z,2x+1是整数
是
是
不是
不是
(3)在(1)的基础上,用量词“所有的”对变量 x进行限定;
关系:
(3)(4)
全称量词命题
(4)在(2)的基础上,用短语”对任意一个”对 变量x进行限定.
下列语句是命题吗 (1)与(3),(2)与(4)之间有什么关系
问题导入
思考:你还有哪些同义替换?
概念辨析
一.全称量词与全称量词命题
1.全称量词:短语“所有的”“任意一个”在逻辑中通常叫做 ____________,并用符号“______”表示.
2.全称量词命题:含有____________的命题,叫做全称量词命题.
3.全称量词命题的表述形式:全称量词命题
“对M中任意一个x,p(x)成立”,可用符号简记为__________________.
全称量词
全称量词
x∈M,p(x)
常见的全称量词还有“一切”“每一个”、“任给” 等
概念辨析
例1.判断下列全称量词命题的真假:
(1)所有的素数都是奇数;
(2);
(3)对任意一个无理数,也是无理数.
解:(1)2是素数,但2不是奇数.所以,全称量词命题“所有的素数都是奇数”是假命题.
(2),总有,因而.所以,全称量词命题“”是真命题.
(3)是无理数,但是有理数.所以,全称量词命题“对任意一个无理数,也是无理数”是假命题.
提示:如果一个大于1 的整数,除1和自身外无其他正因数,则称这个正整数为素数.
要判定全称量词命题“ ”是真命题,需要对集合M中每个元素x,证明 成立;如果在集合M集中找到一个元素x0,使 不成立,那么这个全称量词命题就是假命题.这个方法就是“举反例”.
概念辨析
概念辨析
变式练习1
判断1、2是否是全称量词命题,并尝试判断命题的真假
1、线段垂直平分线上的点到这条线段两个端点的距离相等
2、若x>1,则2x+1>5
3、“含有全称量词的命题”是“全称量词命题”的________条件
真
假
充分不必要
1和2都隐藏了全称量词,但它们是全称量词命题。
关系:
存在量词
下列语句是命题吗 (1)与(3),(2)与(4)之间有什么关系
(1)2x+1=3
(2)x能被2和3整除;
(3)存在一个x∈R,使2x+1=3;
(4)至少有一个x∈Z,x能被2和3整除.
(3)在(1)的基础上,用短语“存在一个”对变量x的取值进行限定,使(3)变成了可以判断真假的语句;
不是
不是
是
是
(4)在(2)的基础上,用“至少有一个”对变量x的取值进行限定,从而使 (4)变成了可以判断真假的语句.
(3)(4)
存在量词命题
概念辨析
概念辨析
二.存在量词与存在量词命题
1.存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做____________,并用符号“_____”表示.
2.存在量词命题:含有存在量词的命题,叫做________________.
3.存在量词命题的表述形式:存在量词命题
“存在M中的元素x,使p(x)成立”,可用符号简记为__________________.
存在量词
存在量词命题
x0∈M,p(x0)
常见的存在量词还有“有些
”“有一个”、“对有些” 等
概念辨析
问题4: 全称量词命题和存在量词命题中是否一定含有全称量词和特称量词?
全称量词命题不一定含有全称量词,比如全称量词命题“正方形是特殊的菱形”,其中没有全称量词。
问题5:短语“至多有一个”是存在量词吗
不是.因为“至多有一个”包含了不存在的情形.
举一些例子?
概念辨析
例2.判断下列存在量词命题的真假:
(1)有一个实数,使;
(2)平面内存在两条相交直线垂直于同一条直线;
(3)有些平行四边形是菱形.
解:(1)由于,因此一元二次方程无实根.所以,存在量词命题“有一个实数,使”是假命题.
(2)由于平面内垂直于同一条直线的两条直线互相平行,因此平面内不可能存在两条相交直线垂直于同一条直线.所以,存在量词命题“平面内存在两条相交直线垂直于同一条直线”是假命题.
(3)由于正方形既是平行四边形又是菱形,所以存在量词命题“有些平行四边形是菱形”是真命题.
要判定存在量词命题“ ”是真命题,需要在集合M中找到一个元素x,使得 成立;如果在集合M中使 成立的元素x不存在,那么这个存在量词命题就是假命题.
概念辨析
随堂练习
1、判断下列命题是全称量词命题还是存在量词命题.
(1)有些实数是无理数;
(2)每一个正方形都是平行四边形
(3)四边形的内角和是360°
(4) x∈R,x2+4x+4≤0;
(5) x∈R,x2+2<0;
(6)方程2x+1=0有整数解.
随堂练习
解:(1)“所有”是全称量词; x∈R,|x|+1>0.
(2)对所有实数a,b,方程ax+b=0恰有一个解;
解:(2)“所有”是全称量词; a,b∈R,方程ax+b=0恰有一个解.
2、指出下列命题中的全称量词或存在量词,并用量词符号“ ”或“ ”表示下列命题.
(1)所有实数x都能使|x|+1>0成立;
(3)存在整数x,y,使得3x-2y=10成立;
解:(3)“存在”是存在量词; x,y∈Z,3x-2y=10.
(4)存在实数m,使得m与m的倒数之和等于1.
随堂练习
随堂练习
(1)已知命题p: x∈{x|1≤x≤4}, x≥a, 若p为真命题,求实数a的取值范围
3、完成下列习题
(2)A={x|1≤x≤4}, x∈A,x-a≤0,求实数a的取值范围
让任意变成存在呢?
4.已知命题p: x∈{-1≤x≤3},x2-a-2≥0,若p为真命题,则实数a的取值范围为 .
{a|a≤-2}
解析:不等式x2-a-2≥0可化为a≤x2-2,
当x∈{-1≤x≤3}时,x2-2的最小值是-2,所以a≤-2.
随堂练习
课堂小结
1.理解全称量词与存在量词的意义
2.掌握判断全称量词命题与存在量词命题真假的方法
3、理解全称量词命题和存在量词命题与恒成立问题和存在性问题的关系
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
