初中数学人教版九下 27.2.3相似三角形应用举例第1课时 教案
文档属性
| 名称 | 初中数学人教版九下 27.2.3相似三角形应用举例第1课时 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 428.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 19:16:44 | ||
图片预览


文档简介
27.2.3相似三角形应用举例
(第1课时)
一、教学内容分析
对于一些大型建筑物的长度或高度(如测金字塔的高度),利用全等知识解决有些不切实际,但是学生有过运用全等三角形知识解决不能直接测量物体长度或高度问题的活动经验,本节课是在已有学习经验基础上,将实际问题转化为数学问题,建立相似三角形模型,利用相似三角形的对应边成比例解决问题,构建恰当的相似三角形,应为本节课的着力点
二、教学目标
1.能够运用相似三角形的知识,解决求不能直接测量的物体的长度和高度等一些实际问题.
2.通过把实际问题转化成有关相似三角形的教学模型,进一步了解数学建模思想,培养分析问题、解决问题的能力.
三、教学重难点
【重点】运用相似三角形有关知识,解决求不能直接测量的物体的长度和高度等一些实际问题.
【难点】构造恰当的相似模型.
四、教学方法
启发式教学与探究式教学相结合来展开分解难点、突出重点.始终体现以学生自主学习及合作交流为主的新课程理念,从学生的经验、生活实际出发,创设情景,引导学生去发现、分析、解决问题.
五、教学过程
(一)创设情境 导入新课
1.著名的科学家阿基米德曾说过,“给我一个支点我可以撬起整个地球”,这句豪言壮语体现的是杠杆原理,同学们知道这个杠杆图里面还藏着今天我们学习的什么数学知识吗?
2.今天我们就一起来学习如何利用生活中的相似图形解决问题.
设计意图:故事讲解,图片的展示,给学生听觉、视觉的冲击,激发学生主动学习的热情;杠杆原理图隐藏着相似三角形的模型,紧扣课题,导入新课.
(二)感受生活 展示模型
1.在阳光下,同一时刻的物高与影长成比例,某一时刻一竹杆高度为2米,影长1.5米,某同学影长1.2米,身高 米.
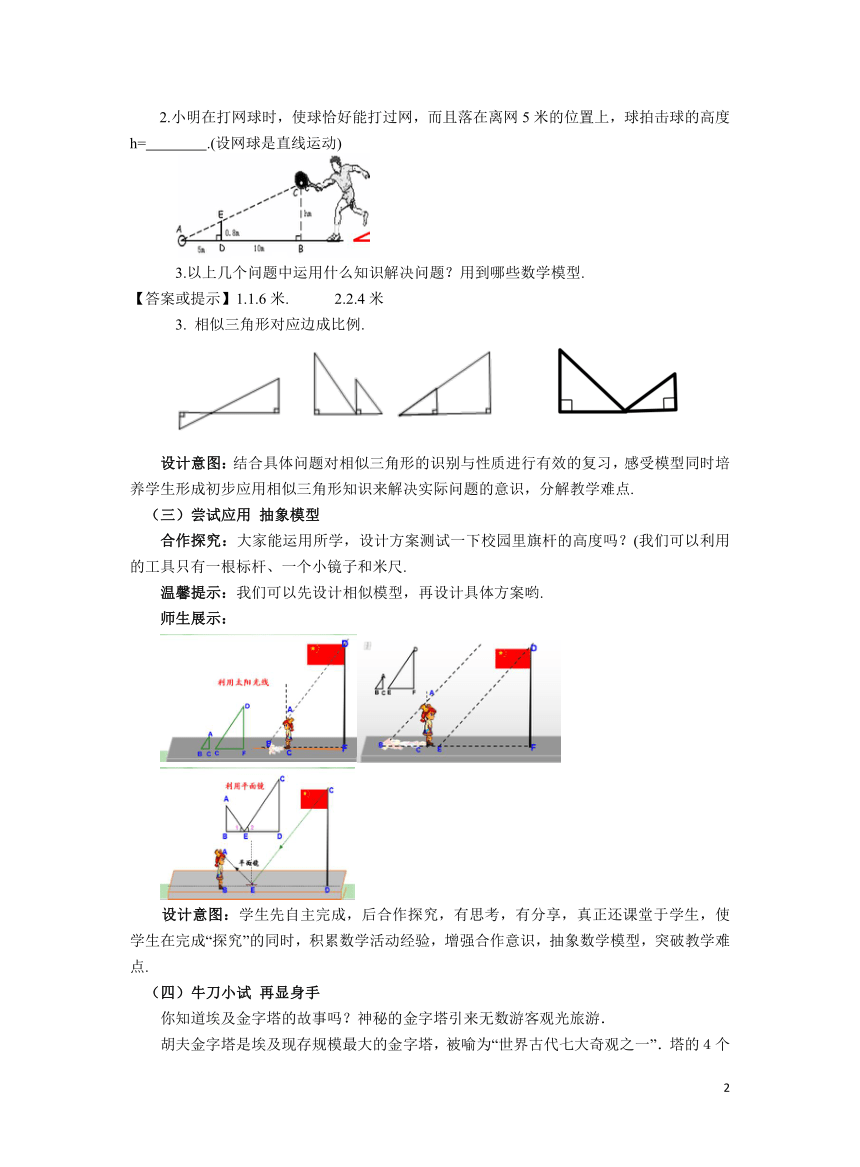
2.小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,球拍击球的高度h= .(设网球是直线运动)
3.以上几个问题中运用什么知识解决问题?用到哪些数学模型.
【答案或提示】1.1.6米. 2.2.4米
3. 相似三角形对应边成比例.
设计意图:结合具体问题对相似三角形的识别与性质进行有效的复习,感受模型同时培养学生形成初步应用相似三角形知识来解决实际问题的意识,分解教学难点.
(三)尝试应用 抽象模型
合作探究:大家能运用所学,设计方案测试一下校园里旗杆的高度吗?(我们可以利用的工具只有一根标杆、一个小镜子和米尺.
温馨提示:我们可以先设计相似模型,再设计具体方案哟.
师生展示:
设计意图:学生先自主完成,后合作探究,有思考,有分享,真正还课堂于学生,使学生在完成“探究”的同时,积累数学活动经验,增强合作意识,抽象数学模型,突破教学难点.
(四)牛刀小试 再显身手
你知道埃及金字塔的故事吗?神秘的金字塔引来无数游客观光旅游.
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”.塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米.据考证,为建成大金字塔,共动用了10万人花了20年时间.该金字塔的原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀,所以高度有所降低.
在古希腊,有一位伟大的科学家叫泰勒斯.一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗?
例4:据传说,古希腊数学家、天文学家泰勒斯曾用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图1,木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
【答案或提示】
解:太阳光是平行线,因此∠BAO=∠EDF
又∠AOB=∠DFE=90°,
∴△ABO∽△DEF
∴
∴
因此金字塔的高度位134m.
设计意图:介绍例题背景,唤醒学生对数学的热爱,通过对例题的分析,让学生体会在实际测量物体的长度或高度时,关键是要构造一个与实物所在三角形相似的三角形,测量出相关线段的长,再运用相似三角形的性质列出比例式解决问题,突破教学重点.
例5:如图2,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.已测得QS=45 m,ST=90 m,QR=60 m,请根据这些数据,计算河宽PQ.
追问:(1)直线QR与ST有什么位置关系,为什么?
(2)图中是否有相似三角形?哪两个三角形相似?
(3)怎样求PQ?
挑战:同学们还能否设计出其它测量河宽的方案?
【答案或提示】
解:∵∠PQR=∠PST=90°,∠P=∠P,
∴△PQR∽△PST
∴
∴
PQ×90=(PQ+45)×60
解得 PQ=90(m)
因此,河宽大约90m.
设计意图:通过例题的分析与讲解,进一步使学生知道在实际测量物体的高度与宽度时,构建相似三角形模型是核心,获取其中某些线段的值是关键,从而突破重点.
(五)课堂练习
1.教材41页1.2题.
2. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( B )
A.4cm B.4.5cm C.5cm D.6cm
3. 如图,数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高为1.2m,地面上的影长为2.6m,请你帮算一下,树高是( 4.45 )m.
设计意图:丰富学生对生活中相似三角形应用的认识,巩固新知.
(六)课堂小结
分享一下这节课你学了哪些知识,探索新知过程中运用了什么数学思想?
设计意图:对所学知识进行梳理,并对知识进一步内化,系统化.
(七)作业布置
A组:教材43页9.10题,57页7题.
B组:1. 如图,广场上有一盏路灯挂在高9.6m的电线杆顶上,记电线杆的底部为O.把路灯看成一个点光源,一名身高1.6m的女孩站在点P处, OP=2m,若女孩以2m为半径绕着电线杆走一个圆圈,则女孩的影子扫过的图形的面积为( C )
A. B. C. D.
【解析】根据题意画出图形,利用三角形相似列方程求出影子的长,再计算人影扫过的面积.
如下图所示:
设AP=x,由题意可知:△COA∽△BPA,∴,
代入数据CO=9.6,BP=1.6,OP=2,
∴,解得,
∴所以人影扫过的面积是,
2.请你利用相似三角形的有关知识,设计一种方案,求出图中所示零件内径AB的值.
六、板书设计
27.2.3相似三角形应用举例
一、相似中的基本模型
二、解决问题
例4: 例5:
三、数学思想: 建模思想、转化思想
七、课后反思
本节课是相似三角形基础知识的应用、延伸与拓展,教学设计使学生在富有故事性和现实性的数学情景问题中学会运用两个三角形相似解决实际问题.在教学中突出了审题画图意识,明确数量关系解决问题的数学建模过程,培养了学生分析问题、解决问题的能力以及抽象概括能力.
1
(第1课时)
一、教学内容分析
对于一些大型建筑物的长度或高度(如测金字塔的高度),利用全等知识解决有些不切实际,但是学生有过运用全等三角形知识解决不能直接测量物体长度或高度问题的活动经验,本节课是在已有学习经验基础上,将实际问题转化为数学问题,建立相似三角形模型,利用相似三角形的对应边成比例解决问题,构建恰当的相似三角形,应为本节课的着力点
二、教学目标
1.能够运用相似三角形的知识,解决求不能直接测量的物体的长度和高度等一些实际问题.
2.通过把实际问题转化成有关相似三角形的教学模型,进一步了解数学建模思想,培养分析问题、解决问题的能力.
三、教学重难点
【重点】运用相似三角形有关知识,解决求不能直接测量的物体的长度和高度等一些实际问题.
【难点】构造恰当的相似模型.
四、教学方法
启发式教学与探究式教学相结合来展开分解难点、突出重点.始终体现以学生自主学习及合作交流为主的新课程理念,从学生的经验、生活实际出发,创设情景,引导学生去发现、分析、解决问题.
五、教学过程
(一)创设情境 导入新课
1.著名的科学家阿基米德曾说过,“给我一个支点我可以撬起整个地球”,这句豪言壮语体现的是杠杆原理,同学们知道这个杠杆图里面还藏着今天我们学习的什么数学知识吗?
2.今天我们就一起来学习如何利用生活中的相似图形解决问题.
设计意图:故事讲解,图片的展示,给学生听觉、视觉的冲击,激发学生主动学习的热情;杠杆原理图隐藏着相似三角形的模型,紧扣课题,导入新课.
(二)感受生活 展示模型
1.在阳光下,同一时刻的物高与影长成比例,某一时刻一竹杆高度为2米,影长1.5米,某同学影长1.2米,身高 米.
2.小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,球拍击球的高度h= .(设网球是直线运动)
3.以上几个问题中运用什么知识解决问题?用到哪些数学模型.
【答案或提示】1.1.6米. 2.2.4米
3. 相似三角形对应边成比例.
设计意图:结合具体问题对相似三角形的识别与性质进行有效的复习,感受模型同时培养学生形成初步应用相似三角形知识来解决实际问题的意识,分解教学难点.
(三)尝试应用 抽象模型
合作探究:大家能运用所学,设计方案测试一下校园里旗杆的高度吗?(我们可以利用的工具只有一根标杆、一个小镜子和米尺.
温馨提示:我们可以先设计相似模型,再设计具体方案哟.
师生展示:
设计意图:学生先自主完成,后合作探究,有思考,有分享,真正还课堂于学生,使学生在完成“探究”的同时,积累数学活动经验,增强合作意识,抽象数学模型,突破教学难点.
(四)牛刀小试 再显身手
你知道埃及金字塔的故事吗?神秘的金字塔引来无数游客观光旅游.
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”.塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米.据考证,为建成大金字塔,共动用了10万人花了20年时间.该金字塔的原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀,所以高度有所降低.
在古希腊,有一位伟大的科学家叫泰勒斯.一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗?
例4:据传说,古希腊数学家、天文学家泰勒斯曾用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图1,木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
【答案或提示】
解:太阳光是平行线,因此∠BAO=∠EDF
又∠AOB=∠DFE=90°,
∴△ABO∽△DEF
∴
∴
因此金字塔的高度位134m.
设计意图:介绍例题背景,唤醒学生对数学的热爱,通过对例题的分析,让学生体会在实际测量物体的长度或高度时,关键是要构造一个与实物所在三角形相似的三角形,测量出相关线段的长,再运用相似三角形的性质列出比例式解决问题,突破教学重点.
例5:如图2,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.已测得QS=45 m,ST=90 m,QR=60 m,请根据这些数据,计算河宽PQ.
追问:(1)直线QR与ST有什么位置关系,为什么?
(2)图中是否有相似三角形?哪两个三角形相似?
(3)怎样求PQ?
挑战:同学们还能否设计出其它测量河宽的方案?
【答案或提示】
解:∵∠PQR=∠PST=90°,∠P=∠P,
∴△PQR∽△PST
∴
∴
PQ×90=(PQ+45)×60
解得 PQ=90(m)
因此,河宽大约90m.
设计意图:通过例题的分析与讲解,进一步使学生知道在实际测量物体的高度与宽度时,构建相似三角形模型是核心,获取其中某些线段的值是关键,从而突破重点.
(五)课堂练习
1.教材41页1.2题.
2. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( B )
A.4cm B.4.5cm C.5cm D.6cm
3. 如图,数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高为1.2m,地面上的影长为2.6m,请你帮算一下,树高是( 4.45 )m.
设计意图:丰富学生对生活中相似三角形应用的认识,巩固新知.
(六)课堂小结
分享一下这节课你学了哪些知识,探索新知过程中运用了什么数学思想?
设计意图:对所学知识进行梳理,并对知识进一步内化,系统化.
(七)作业布置
A组:教材43页9.10题,57页7题.
B组:1. 如图,广场上有一盏路灯挂在高9.6m的电线杆顶上,记电线杆的底部为O.把路灯看成一个点光源,一名身高1.6m的女孩站在点P处, OP=2m,若女孩以2m为半径绕着电线杆走一个圆圈,则女孩的影子扫过的图形的面积为( C )
A. B. C. D.
【解析】根据题意画出图形,利用三角形相似列方程求出影子的长,再计算人影扫过的面积.
如下图所示:
设AP=x,由题意可知:△COA∽△BPA,∴,
代入数据CO=9.6,BP=1.6,OP=2,
∴,解得,
∴所以人影扫过的面积是,
2.请你利用相似三角形的有关知识,设计一种方案,求出图中所示零件内径AB的值.
六、板书设计
27.2.3相似三角形应用举例
一、相似中的基本模型
二、解决问题
例4: 例5:
三、数学思想: 建模思想、转化思想
七、课后反思
本节课是相似三角形基础知识的应用、延伸与拓展,教学设计使学生在富有故事性和现实性的数学情景问题中学会运用两个三角形相似解决实际问题.在教学中突出了审题画图意识,明确数量关系解决问题的数学建模过程,培养了学生分析问题、解决问题的能力以及抽象概括能力.
1
