初中数学人教版九下27.2.1 相似三角形的判定 第(2)课时 同步检测(含解析)
文档属性
| 名称 | 初中数学人教版九下27.2.1 相似三角形的判定 第(2)课时 同步检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 224.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 19:24:17 | ||
图片预览


文档简介
27.2.1 相似三角形的判定(2)
一、选择题
1.将一个三角形的各边都缩小到原来的后,得到三角形与原三角形( )
A.一定不相似 B.不一定相似 C.无法判断是否相似 D.一定相似
2.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
3.如图,在三角形纸片ABC中,AB=9,AC=6,BC=12,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
4.如图所示,网格中相似的两个三角形是( )
A.①与④ B.②与③ C.①与⑤ D.②与⑤
二、填空题
5.如图,已知,若使△ABC∽△ADE成立_____(只添一种即可).
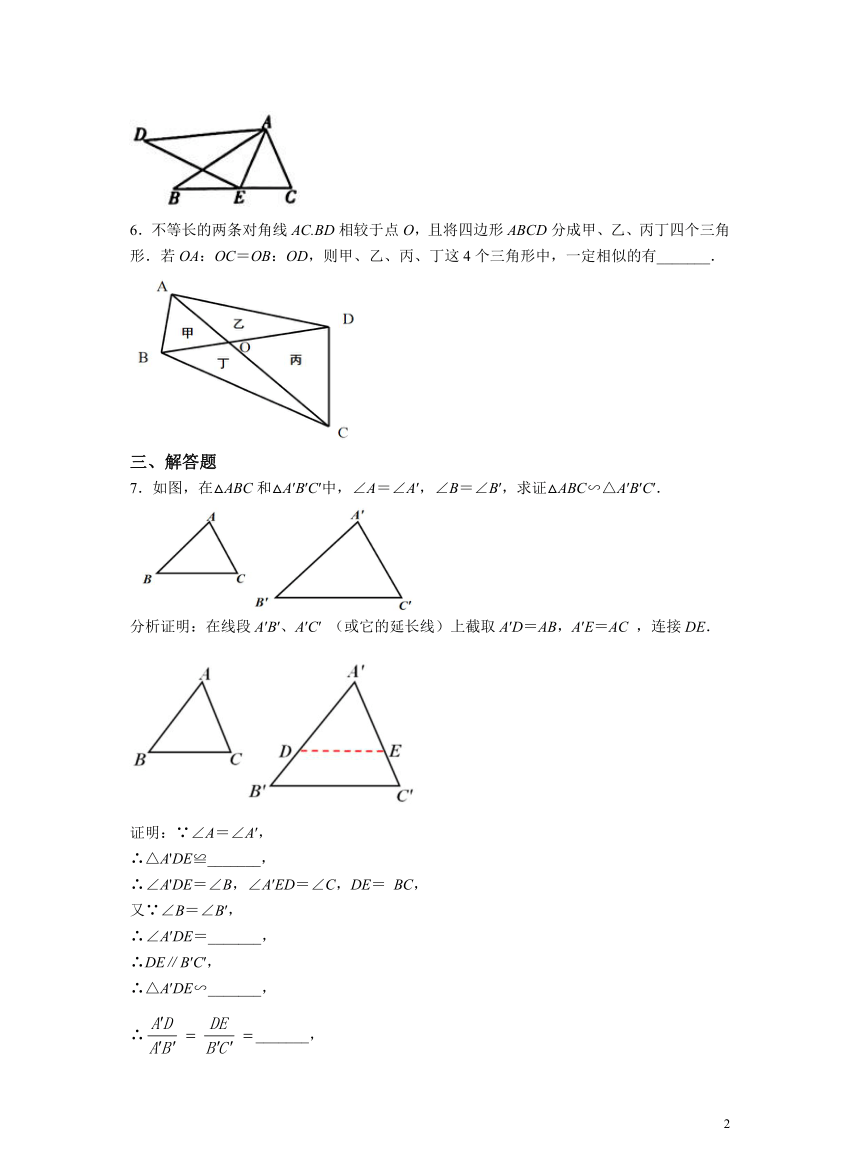
6.不等长的两条对角线AC.BD相较于点O,且将四边形ABCD分成甲、乙、丙丁四个三角形.若OA:OC=OB:OD,则甲、乙、丙、丁这4个三角形中,一定相似的有_______.
三、解答题
7.如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,求证△ABC∽△A′B′C′.
分析证明:在线段A′B′、A′C′ (或它的延长线)上截取A′D=AB,A′E=AC ,连接DE.
证明:∵∠A=∠A′,
∴△A'DE≌_______,
∴∠A'DE=∠B,∠A′ED=∠C,DE= BC,
又∵∠B=∠B′,
∴∠A′DE=_______,
∴DE∥B′C′,
∴△A′DE∽_______,
∴_______,
∵∠A=∠A′,∠B=∠B′, ∠C=∠C′,
∴△ABC∽△A′B′C′.
8.如图,点E在AB上,CE∥BD,BE=3EC,BD=3EA,求证:△BDE∽△EAC.
9.如图所示,判断△ABD和△ABC相似吗?并说明理由.
10.如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °,BC= ;
(2)判断△ABC和△DEF是否相似,并证明你的结论.
1
参考答案
1.D
【解析】根据题意可得原三角形的各边与得到的三角形的各边比均为,再由三边对应成比例的两个三角形相似,即可求解.
【详解】解:∵将一个三角形的各边都缩小到原来的,
∴原三角形的各边与得到的三角形的各边比均为,
∴得到三角形与原三角形一定相似.
故选:D
【点睛】本题主要考查了相似三角形的判定,熟练掌握相似三角形的判定定理是解题的关键.
2.B
【解析】根据已知可求出△ABC三边的长,同理可求出阴影部分的各边长,从而根据相似三角形的三边对应成比例即可得到答案.
【详解】解:∵小正方形的边长均为1,
∴△ABC三边按照从短到长排列分别为:,,;
选项A:三角形三边按照从短到长排列分别为:,,3;
选项B:三角形三边按照从短到长排列分别为:,,;
选项C:三角形三边按照从短到长排列分别为:,,;
选项D:三角形三边按照从短到长排列分别为:,,;
其中选项B:,与△ABC三边对应成比例,
故选:B.
【点睛】本题考查了相似三角形的判定方法,属于基础题,熟练掌握相似三角形的判定方法是解题的关键.
3.B
【解析】根据相似三角形的判定分别进行判断即可得出答案即可.
【详解】解:在三角形纸片ABC中,AB=9,AC=6,BC=12.
A.因为 ,对应边,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.因为,对应边,又∠A=∠A,故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
C.因为,对应边,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D.因为,对应边,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确利用相似三角形两边比值相等切夹角相等的两三角形相似是解题关键.
4.D
【解析】
分别根据网格的特点求得各三角形三边的长,根据三边对应成比例判断两三角形相似即可
【详解】解:根据网格的特点,①号三角形的三边长分别为:;
②号三角形的三边长分别为:
③号三角形的三边长分别为:
④号三角形的三边长分别为:
⑤号三角形的三边长分别为:
,
②与⑤相似,故D选项正确,符合题意;其他选项不正确
故选D
【点睛】本题考查了网格中判断相似三角形,分别求得各三角形的边长是解题的关键.
5.∠DAE=∠BAC(不唯一)
【解析】根据相似三角形的判定定理解答即可.
【详解】解:根据“两边成比例且夹角相等的两个三角形相似”可得:∠DAE=∠BAC.
故答案是∠DAE=∠BAC(不唯一).
【点睛】本题主要考查了相似三角形的判定,掌握“两边成比例且夹角相等的两个三角形相似”和“三边成比例的两个三角形相似”是解答本题的关键.
6.甲和丙
7. △ABC ∠B' △A'B'C'
8.【详解】∵CE//BD,
∴∠CEA=∠B,
∵BE=3EC,BD=3EA,
∴,
∴ △BDE∽△EAC.
9.相似;理由见解析
【解析】
先求出BC=4,即可得到,再由∠ABD=∠CBA,即可证明
△ABD∽△CBA.
【详解】解:△ABD∽△CBA,理由如下:
∵BD=1,CD=3,
∴BC=BD+CD=4,
∴,
又∵∠ABD=∠CBA,
∴△ABD∽△CBA.
【点睛】本题主要考查了相似三角形的判定,熟练掌握相似三角形的判定条件是解题的关键.
10.(1)135, ;(2)△ABC∽△DEF,证明见解析
【解析】
(1)先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△BGC中利用勾股定理即可求出BC的长.
(2)利用格点三角形的知识求出AB,BC及DE,EF的长度,继而可作出判断.
【详解】解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BGC中,BG=2,CG=2,
∴;
故答案为:135,;
(2)解:相似.理由如下:
∵∠GEF=90°,∠GED=45°;
∴∠DEF=135°
∴
∴
又∵∠ABC=∠CED=135°
∴△ABC∽△DEF.
【点睛】此题主要考查学生对勾股定理和相似三角形的判定的理解和掌握,解答此题的关键是认真观察图形,得出两个三角形角和角,边和边的关系.
答案第1页,共2页
答案第4页,共4页
一、选择题
1.将一个三角形的各边都缩小到原来的后,得到三角形与原三角形( )
A.一定不相似 B.不一定相似 C.无法判断是否相似 D.一定相似
2.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
3.如图,在三角形纸片ABC中,AB=9,AC=6,BC=12,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
4.如图所示,网格中相似的两个三角形是( )
A.①与④ B.②与③ C.①与⑤ D.②与⑤
二、填空题
5.如图,已知,若使△ABC∽△ADE成立_____(只添一种即可).
6.不等长的两条对角线AC.BD相较于点O,且将四边形ABCD分成甲、乙、丙丁四个三角形.若OA:OC=OB:OD,则甲、乙、丙、丁这4个三角形中,一定相似的有_______.
三、解答题
7.如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,求证△ABC∽△A′B′C′.
分析证明:在线段A′B′、A′C′ (或它的延长线)上截取A′D=AB,A′E=AC ,连接DE.
证明:∵∠A=∠A′,
∴△A'DE≌_______,
∴∠A'DE=∠B,∠A′ED=∠C,DE= BC,
又∵∠B=∠B′,
∴∠A′DE=_______,
∴DE∥B′C′,
∴△A′DE∽_______,
∴_______,
∵∠A=∠A′,∠B=∠B′, ∠C=∠C′,
∴△ABC∽△A′B′C′.
8.如图,点E在AB上,CE∥BD,BE=3EC,BD=3EA,求证:△BDE∽△EAC.
9.如图所示,判断△ABD和△ABC相似吗?并说明理由.
10.如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °,BC= ;
(2)判断△ABC和△DEF是否相似,并证明你的结论.
1
参考答案
1.D
【解析】根据题意可得原三角形的各边与得到的三角形的各边比均为,再由三边对应成比例的两个三角形相似,即可求解.
【详解】解:∵将一个三角形的各边都缩小到原来的,
∴原三角形的各边与得到的三角形的各边比均为,
∴得到三角形与原三角形一定相似.
故选:D
【点睛】本题主要考查了相似三角形的判定,熟练掌握相似三角形的判定定理是解题的关键.
2.B
【解析】根据已知可求出△ABC三边的长,同理可求出阴影部分的各边长,从而根据相似三角形的三边对应成比例即可得到答案.
【详解】解:∵小正方形的边长均为1,
∴△ABC三边按照从短到长排列分别为:,,;
选项A:三角形三边按照从短到长排列分别为:,,3;
选项B:三角形三边按照从短到长排列分别为:,,;
选项C:三角形三边按照从短到长排列分别为:,,;
选项D:三角形三边按照从短到长排列分别为:,,;
其中选项B:,与△ABC三边对应成比例,
故选:B.
【点睛】本题考查了相似三角形的判定方法,属于基础题,熟练掌握相似三角形的判定方法是解题的关键.
3.B
【解析】根据相似三角形的判定分别进行判断即可得出答案即可.
【详解】解:在三角形纸片ABC中,AB=9,AC=6,BC=12.
A.因为 ,对应边,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.因为,对应边,又∠A=∠A,故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
C.因为,对应边,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D.因为,对应边,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确利用相似三角形两边比值相等切夹角相等的两三角形相似是解题关键.
4.D
【解析】
分别根据网格的特点求得各三角形三边的长,根据三边对应成比例判断两三角形相似即可
【详解】解:根据网格的特点,①号三角形的三边长分别为:;
②号三角形的三边长分别为:
③号三角形的三边长分别为:
④号三角形的三边长分别为:
⑤号三角形的三边长分别为:
,
②与⑤相似,故D选项正确,符合题意;其他选项不正确
故选D
【点睛】本题考查了网格中判断相似三角形,分别求得各三角形的边长是解题的关键.
5.∠DAE=∠BAC(不唯一)
【解析】根据相似三角形的判定定理解答即可.
【详解】解:根据“两边成比例且夹角相等的两个三角形相似”可得:∠DAE=∠BAC.
故答案是∠DAE=∠BAC(不唯一).
【点睛】本题主要考查了相似三角形的判定,掌握“两边成比例且夹角相等的两个三角形相似”和“三边成比例的两个三角形相似”是解答本题的关键.
6.甲和丙
7. △ABC ∠B' △A'B'C'
8.【详解】∵CE//BD,
∴∠CEA=∠B,
∵BE=3EC,BD=3EA,
∴,
∴ △BDE∽△EAC.
9.相似;理由见解析
【解析】
先求出BC=4,即可得到,再由∠ABD=∠CBA,即可证明
△ABD∽△CBA.
【详解】解:△ABD∽△CBA,理由如下:
∵BD=1,CD=3,
∴BC=BD+CD=4,
∴,
又∵∠ABD=∠CBA,
∴△ABD∽△CBA.
【点睛】本题主要考查了相似三角形的判定,熟练掌握相似三角形的判定条件是解题的关键.
10.(1)135, ;(2)△ABC∽△DEF,证明见解析
【解析】
(1)先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△BGC中利用勾股定理即可求出BC的长.
(2)利用格点三角形的知识求出AB,BC及DE,EF的长度,继而可作出判断.
【详解】解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BGC中,BG=2,CG=2,
∴;
故答案为:135,;
(2)解:相似.理由如下:
∵∠GEF=90°,∠GED=45°;
∴∠DEF=135°
∴
∴
又∵∠ABC=∠CED=135°
∴△ABC∽△DEF.
【点睛】此题主要考查学生对勾股定理和相似三角形的判定的理解和掌握,解答此题的关键是认真观察图形,得出两个三角形角和角,边和边的关系.
答案第1页,共2页
答案第4页,共4页
