初中数学人教版九下27.2.1相似三角形的判定(第3课时) 教案
文档属性
| 名称 | 初中数学人教版九下27.2.1相似三角形的判定(第3课时) 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 19:31:15 | ||
图片预览



文档简介
27.2.1相似三角形的判定
(第3课时)
一、教学内容分析
本节课是相似三角形的判定的第三课时,学生已经积累了丰富的数学活动经验,基本掌握探究两三角形相似的一般思路,本节课是对研究几何图形的经验、基本思路、方法的再强化,相似三角形的判定方法证明仍为重点,灵活运用定理解决问题成为难点.
二、教学目标
1. 继续探究两个三角形相似的判定方法,体验用类比、实验操作、分析归纳得出数学结论的过程, 在教学过程中渗透类比、转化等数学思想.
2. 掌握“两角分别相等的两个三角形相似”和判定两直角三角形相似的方法.
3.会运用三角形相似的条件解决简单问题.
三、教学重难点
【重点】掌握“两角分别相等的两个三角形相似”和判定两直角三角形相似的方法.
【难点】运用两个三角形相似的判定方法解决简单问题.
四、教学方法
本节课采用以引导发现法为主,并以讨论法、演示法相结合,意在帮助学生通过直观情景观察和自己动手操作,从自己的实践中获取知识并通过讨论来深化对知识的理解.
五、教学过程
(一)新课导入
1.相似三角形的判定方法有哪些?
2.我们探究相似三角形判定方法的基本思路是什么?
意图:对相似三角形判定方法和基本思路及时进行归纳整理.
效果:复习“旧知”,关联“新知”.
(二)新课讲授
活动一 类比探究 证明定理
1. 类比以上探究三角形相似的方法,猜想两角分别相等的两个三角形相似吗?说说你的方法.
意图:引导学生分别用“寻找生活中的实例”、“画图测量”、“理论证明”等不同角度解决问题.
效果:训练学生多方面、多角度解决问题,培养学生思维的广阔性和灵活性.
2.写出命题“两角分别相等的两个三角形相似“的已知、求证,并完成证明过程.
追问:结合命题的已知,我们需要再找到什么条件证两三角形相似?如何做辅助线?
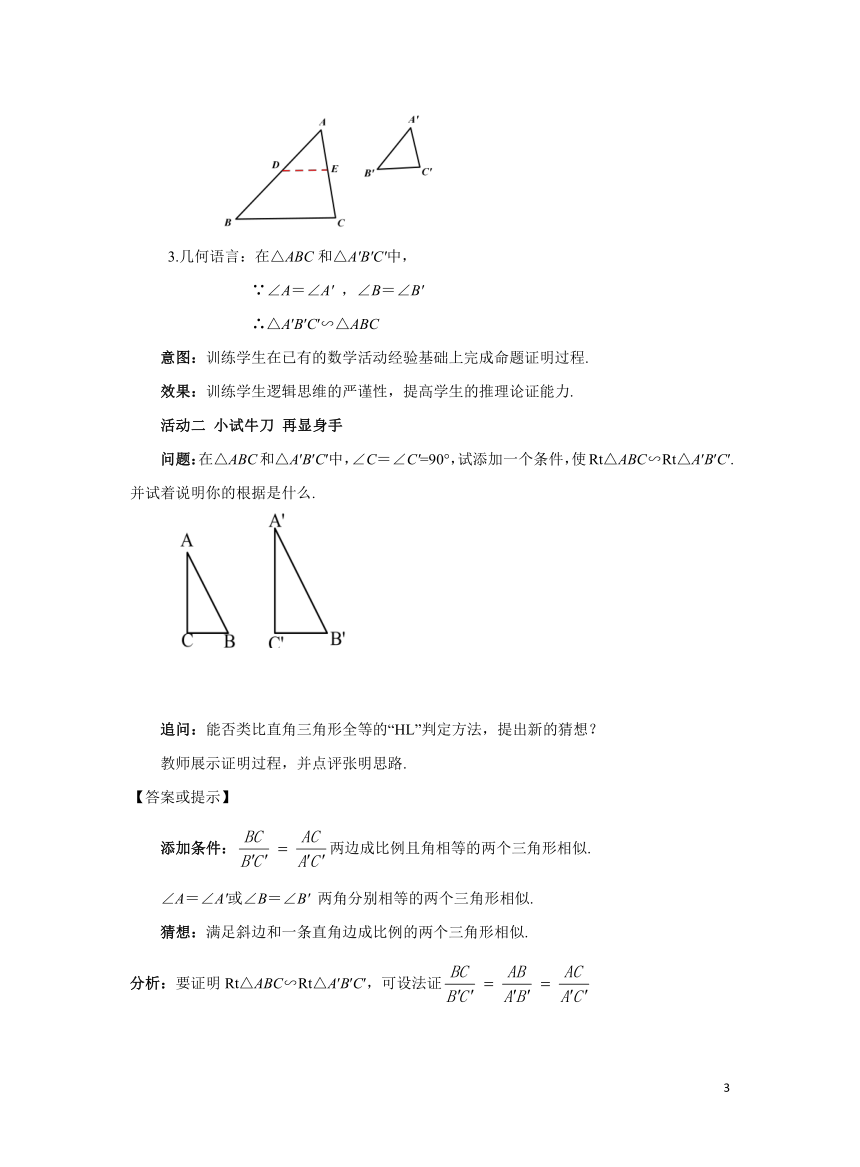
3.写出该定理的几何语言.
【答案或提示】
1.生活实例,两幅三角尺; 画图测量,在边长都是1的方格纸上,任意绘制△ABC和△A'B'C' ,使得∠A=∠A' ,∠B=∠B',计算任意夹一组对应角的两组边是否成比例; 写出已知、求证,进行严谨证明.
2.已知: △ABC和△A'B'C' ,使得∠A=∠A' ,∠B=∠B',
求证:△ABC∽△A′B′C′.
证明:在△ABC的边AB(或延长线)上截取AD= A' B', 过点 D 作 DE∥BC.
∵ DE∥BC
∴△ADE∽△ABC.
∵∠B=∠B′
∴∠ADE=∠B′
又∵ AD=A′B′,∠A=∠A′,
∴△ADE ≌△A′B′C′,
∴△A′B′C′∽△ABC.
3.几何语言:在△ABC和△A'B'C'中,
∵∠A=∠A' ,∠B=∠B'
∴△A′B′C′∽△ABC
意图:训练学生在已有的数学活动经验基础上完成命题证明过程.
效果:训练学生逻辑思维的严谨性,提高学生的推理论证能力.
活动二 小试牛刀 再显身手
问题:在△ABC和△A′B′C′中,∠C=∠C'=90°,试添加一个条件,使Rt△ABC∽Rt△A′B′C′.并试着说明你的根据是什么.
追问:能否类比直角三角形全等的“HL”判定方法,提出新的猜想?
教师展示证明过程,并点评张明思路.
【答案或提示】
添加条件:两边成比例且角相等的两个三角形相似.
∠A=∠A'或∠B=∠B' 两角分别相等的两个三角形相似.
猜想:满足斜边和一条直角边成比例的两个三角形相似.
分析:要证明Rt△ABC∽Rt△A′B′C′,可设法证
设,则只需证通过代数计算的方法,利用勾股定理证明.
证明:设,则AB=kA′B′,AC=kA′C′
由勾股定理,得BC=,
∴
∴ Rt△ABC ∽ Rt△A′B′C′.
意图:利用所学相似三角形判定方法解决直角三角形的相似.
效果:巩固相似三角形判定定理,丰富学生的分析问题、解决问题的活动经验.
活动三 精讲例题 拓展延伸
例2,如图,在Rt△ABC 中,∠C=90°,AB=10,AC=8.E是AC 一点,AE =5,ED⊥AB,垂足为D. 求AD的长.
变式1:已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,
(1).图中有几对相似的三角形?写一写
(2).若AB=10,AC=8,求AD的长.
变式2:如图:在△ABC中,D为边AB上一点,连接CD,能使△ABC∽△ACD的条件是:
①∠ACD=∠B ②∠ACD=∠B ③ ④AC2=AD﹒AB ⑤
若△ABC∽△ACD,AB=10,AC=8,CD=4.8, AD= ,此时∠ACB= °
【答案或提示】例2解:∵ ED⊥AB,
∴∠EDA=90°.
又∵∠C=90°,∠A=∠A,
∴ △AED ∽△ABC.
∴
∴
变式1:(1)3对,△ABC∽△ACD,△ABC∽△CBD, △CBD∽△ACD
(2)利用△ABC∽△ACD相似,AC2=AD﹒AB,AD=6.4
变式2:① ② ③ ④ ,6.4 ,90(利用勾股定理逆定理证得△ACD为直角三角形,再利用相似三角形对应角相等求∠ACB度数.)
意图:巩固新知,融会贯通.
效果:通过变式训练,训练学生的思维发散性和敏捷性,优化思维品质.
(三)课堂练习
1.教材36页1.3题.
2. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( C )
3.如图,⊙O 的弦 AB,CD 相交于点 P,若 PA=3, PB = 8,PC = 4,则 PD = 6 .
意图:利用“两角分别相等的两个三角形相似”解决简单问题.
效果:巩固新知.
(四)课堂小结
这节课我们的收获是什么?试着分别从知识与技能、过程与方法等方面分享一下.
意图:从知识与技能、过程与方法等方面引导学生总结收获.
效果:在获得知识的同时,习得必要的数学学习方法,感悟数学思想方法的重要意义.
(五) 作业布置
A组:教材43页7题,58页8.9题.
B组:1.如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,,则AE的长为 7 .
【解析】结合图形符合一线三等角基本模型,易证△ABD∽△DCE,则,带入求值CE=2,则AE=7
2.如图,BE是△ABC的外接圆O的直径,CD是△ABC的高,求证:
【解析】证明: 连接CE,则∠A=∠E.
又∵BE是△ABC的外接圆O的直径,
∴∠BCE=90°=∠ADC,
∵∠A=∠E,∠BCE=∠ADC,
∴△ACD∽△EBC.
∴
3.如图,已知:∠ACB =∠ADC = 90°,AD = 2,CD =,当AB 的长为多少时,△ACB 与△ADC相似.
【解析】当两个相似三角形不是用相似符号连接时,要根据对应角或对应比不同分情况讨论.
详解:解:∵∠ADC = 90°,AD = 2,CD =,
当△ACB 与△ADC相似时,有两种情况:
(1)当∠CAD =∠BAC时,
有;
(2) 当∠ACD =∠BAC时,
∴当AB为3或时,这两个直角三角形相似.
意图:A组题目注重基础知识的直接运用,B组题目有一定灵活性,适用于学有余力的同学.
效果:布置分层作业,照顾不同学情的学生,进行自我检测.
六、板书设计
27.2.1相似三角形的判定
1.相似三角形判定方法.
2.分别相等的两个三角形相似.
几何语言: 在△ABC和△A'B'C'中,
∵∠A=∠A' ,∠B=∠B'
∴△A′B′C′∽△ABC
例题:
变式1:
变式2:
七、课后反思
《义务教育数学课程标准》指出:有效的数学学习活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学习数学的重要方式. 为了充分体现《义务教育数学课程》的要求,培养学生的动手实践能力,逻辑推理能力,积累丰富的数学活动经验,这节课主要采用动手实践,自主探索与合作交流的学习方法,使学生积极参与教学过程,在教学过程中展开思维,培养学生提出问题、分析问题、解决问题的能力,进一步理解观察、类比、分析、转化等数学思想方法.1
(第3课时)
一、教学内容分析
本节课是相似三角形的判定的第三课时,学生已经积累了丰富的数学活动经验,基本掌握探究两三角形相似的一般思路,本节课是对研究几何图形的经验、基本思路、方法的再强化,相似三角形的判定方法证明仍为重点,灵活运用定理解决问题成为难点.
二、教学目标
1. 继续探究两个三角形相似的判定方法,体验用类比、实验操作、分析归纳得出数学结论的过程, 在教学过程中渗透类比、转化等数学思想.
2. 掌握“两角分别相等的两个三角形相似”和判定两直角三角形相似的方法.
3.会运用三角形相似的条件解决简单问题.
三、教学重难点
【重点】掌握“两角分别相等的两个三角形相似”和判定两直角三角形相似的方法.
【难点】运用两个三角形相似的判定方法解决简单问题.
四、教学方法
本节课采用以引导发现法为主,并以讨论法、演示法相结合,意在帮助学生通过直观情景观察和自己动手操作,从自己的实践中获取知识并通过讨论来深化对知识的理解.
五、教学过程
(一)新课导入
1.相似三角形的判定方法有哪些?
2.我们探究相似三角形判定方法的基本思路是什么?
意图:对相似三角形判定方法和基本思路及时进行归纳整理.
效果:复习“旧知”,关联“新知”.
(二)新课讲授
活动一 类比探究 证明定理
1. 类比以上探究三角形相似的方法,猜想两角分别相等的两个三角形相似吗?说说你的方法.
意图:引导学生分别用“寻找生活中的实例”、“画图测量”、“理论证明”等不同角度解决问题.
效果:训练学生多方面、多角度解决问题,培养学生思维的广阔性和灵活性.
2.写出命题“两角分别相等的两个三角形相似“的已知、求证,并完成证明过程.
追问:结合命题的已知,我们需要再找到什么条件证两三角形相似?如何做辅助线?
3.写出该定理的几何语言.
【答案或提示】
1.生活实例,两幅三角尺; 画图测量,在边长都是1的方格纸上,任意绘制△ABC和△A'B'C' ,使得∠A=∠A' ,∠B=∠B',计算任意夹一组对应角的两组边是否成比例; 写出已知、求证,进行严谨证明.
2.已知: △ABC和△A'B'C' ,使得∠A=∠A' ,∠B=∠B',
求证:△ABC∽△A′B′C′.
证明:在△ABC的边AB(或延长线)上截取AD= A' B', 过点 D 作 DE∥BC.
∵ DE∥BC
∴△ADE∽△ABC.
∵∠B=∠B′
∴∠ADE=∠B′
又∵ AD=A′B′,∠A=∠A′,
∴△ADE ≌△A′B′C′,
∴△A′B′C′∽△ABC.
3.几何语言:在△ABC和△A'B'C'中,
∵∠A=∠A' ,∠B=∠B'
∴△A′B′C′∽△ABC
意图:训练学生在已有的数学活动经验基础上完成命题证明过程.
效果:训练学生逻辑思维的严谨性,提高学生的推理论证能力.
活动二 小试牛刀 再显身手
问题:在△ABC和△A′B′C′中,∠C=∠C'=90°,试添加一个条件,使Rt△ABC∽Rt△A′B′C′.并试着说明你的根据是什么.
追问:能否类比直角三角形全等的“HL”判定方法,提出新的猜想?
教师展示证明过程,并点评张明思路.
【答案或提示】
添加条件:两边成比例且角相等的两个三角形相似.
∠A=∠A'或∠B=∠B' 两角分别相等的两个三角形相似.
猜想:满足斜边和一条直角边成比例的两个三角形相似.
分析:要证明Rt△ABC∽Rt△A′B′C′,可设法证
设,则只需证通过代数计算的方法,利用勾股定理证明.
证明:设,则AB=kA′B′,AC=kA′C′
由勾股定理,得BC=,
∴
∴ Rt△ABC ∽ Rt△A′B′C′.
意图:利用所学相似三角形判定方法解决直角三角形的相似.
效果:巩固相似三角形判定定理,丰富学生的分析问题、解决问题的活动经验.
活动三 精讲例题 拓展延伸
例2,如图,在Rt△ABC 中,∠C=90°,AB=10,AC=8.E是AC 一点,AE =5,ED⊥AB,垂足为D. 求AD的长.
变式1:已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,
(1).图中有几对相似的三角形?写一写
(2).若AB=10,AC=8,求AD的长.
变式2:如图:在△ABC中,D为边AB上一点,连接CD,能使△ABC∽△ACD的条件是:
①∠ACD=∠B ②∠ACD=∠B ③ ④AC2=AD﹒AB ⑤
若△ABC∽△ACD,AB=10,AC=8,CD=4.8, AD= ,此时∠ACB= °
【答案或提示】例2解:∵ ED⊥AB,
∴∠EDA=90°.
又∵∠C=90°,∠A=∠A,
∴ △AED ∽△ABC.
∴
∴
变式1:(1)3对,△ABC∽△ACD,△ABC∽△CBD, △CBD∽△ACD
(2)利用△ABC∽△ACD相似,AC2=AD﹒AB,AD=6.4
变式2:① ② ③ ④ ,6.4 ,90(利用勾股定理逆定理证得△ACD为直角三角形,再利用相似三角形对应角相等求∠ACB度数.)
意图:巩固新知,融会贯通.
效果:通过变式训练,训练学生的思维发散性和敏捷性,优化思维品质.
(三)课堂练习
1.教材36页1.3题.
2. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( C )
3.如图,⊙O 的弦 AB,CD 相交于点 P,若 PA=3, PB = 8,PC = 4,则 PD = 6 .
意图:利用“两角分别相等的两个三角形相似”解决简单问题.
效果:巩固新知.
(四)课堂小结
这节课我们的收获是什么?试着分别从知识与技能、过程与方法等方面分享一下.
意图:从知识与技能、过程与方法等方面引导学生总结收获.
效果:在获得知识的同时,习得必要的数学学习方法,感悟数学思想方法的重要意义.
(五) 作业布置
A组:教材43页7题,58页8.9题.
B组:1.如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,,则AE的长为 7 .
【解析】结合图形符合一线三等角基本模型,易证△ABD∽△DCE,则,带入求值CE=2,则AE=7
2.如图,BE是△ABC的外接圆O的直径,CD是△ABC的高,求证:
【解析】证明: 连接CE,则∠A=∠E.
又∵BE是△ABC的外接圆O的直径,
∴∠BCE=90°=∠ADC,
∵∠A=∠E,∠BCE=∠ADC,
∴△ACD∽△EBC.
∴
3.如图,已知:∠ACB =∠ADC = 90°,AD = 2,CD =,当AB 的长为多少时,△ACB 与△ADC相似.
【解析】当两个相似三角形不是用相似符号连接时,要根据对应角或对应比不同分情况讨论.
详解:解:∵∠ADC = 90°,AD = 2,CD =,
当△ACB 与△ADC相似时,有两种情况:
(1)当∠CAD =∠BAC时,
有;
(2) 当∠ACD =∠BAC时,
∴当AB为3或时,这两个直角三角形相似.
意图:A组题目注重基础知识的直接运用,B组题目有一定灵活性,适用于学有余力的同学.
效果:布置分层作业,照顾不同学情的学生,进行自我检测.
六、板书设计
27.2.1相似三角形的判定
1.相似三角形判定方法.
2.分别相等的两个三角形相似.
几何语言: 在△ABC和△A'B'C'中,
∵∠A=∠A' ,∠B=∠B'
∴△A′B′C′∽△ABC
例题:
变式1:
变式2:
七、课后反思
《义务教育数学课程标准》指出:有效的数学学习活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学习数学的重要方式. 为了充分体现《义务教育数学课程》的要求,培养学生的动手实践能力,逻辑推理能力,积累丰富的数学活动经验,这节课主要采用动手实践,自主探索与合作交流的学习方法,使学生积极参与教学过程,在教学过程中展开思维,培养学生提出问题、分析问题、解决问题的能力,进一步理解观察、类比、分析、转化等数学思想方法.1
