初中数学人教版九下27.2.2相似三角形的性质 同步检测(含解析)
文档属性
| 名称 | 初中数学人教版九下27.2.2相似三角形的性质 同步检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 210.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 19:32:18 | ||
图片预览



文档简介
27.2.2相似三角形的性质
一、单选题
1.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )
A.3:5 B.9:25 C.5:3 D.25:9
2.若△ABC∽△A'B'C',相似比为1:2,则△ABC与△A'B'C'的面积的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,△ ABC中,点D、E分别在AB、AC上,且,下列结论正确的是( )
A.DE:BC=1:2 B.△ ADE与△ABC的面积比为1:3
C.△ ADE与△ABC的周长比为1:2 D.DE∥BC
4.如图,△ABC中,DE∥FG∥BC,且AD:DF:FB=1:1:1,则△ABC被分成的三部分面积之比S1:S2:S3=( )
A.1∶1∶1 B.1∶2∶3 C.1∶3∶5 D.1: :
5.如图在△ABC中,点E是AB边上的点,点F是AC边上的点,且EF∥BC,AE:EB=3:1,点D是AE中点,若△ABC的面积为32,则△DEF的面积为( )
A.18 B.12 C.10 D.9
6.已知△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,若BC边上的中线长为1,则EF边上的中线长是( )
A. B.2 C.3 D.4
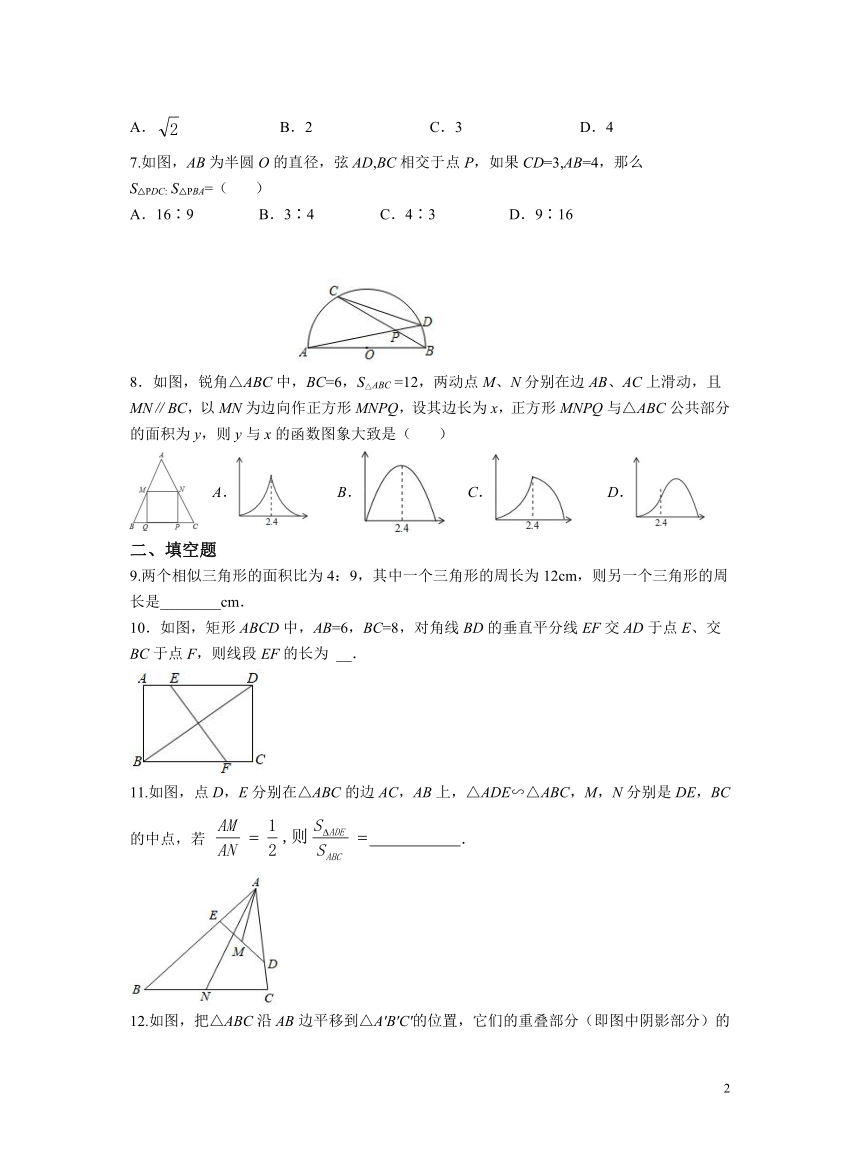
7.如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么
S△PDC: S△PBA=( )
A.16∶9 B.3∶4 C.4∶3 D.9∶16
8.如图,锐角△ABC中,BC=6,S△ABC =12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MNPQ,设其边长为x,正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
A. B. C. D.
二、填空题
9.两个相似三角形的面积比为4:9,其中一个三角形的周长为12cm,则另一个三角形的周长是________cm.
10.如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 __.
11.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若 .
12.如图,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC的面积的,若AB=5cm,则此三角形移动的距离AA'= cm.
三、解答题
13.如图,在△ABC和△DEF中,G,H分别是边BC和EF的中点,已知AB=2DE,AC=2DF,∠BAC=∠EDF.
(1)中线AG与DH的比是多少?
(2)△ABC和△DEF的面积比是多少?
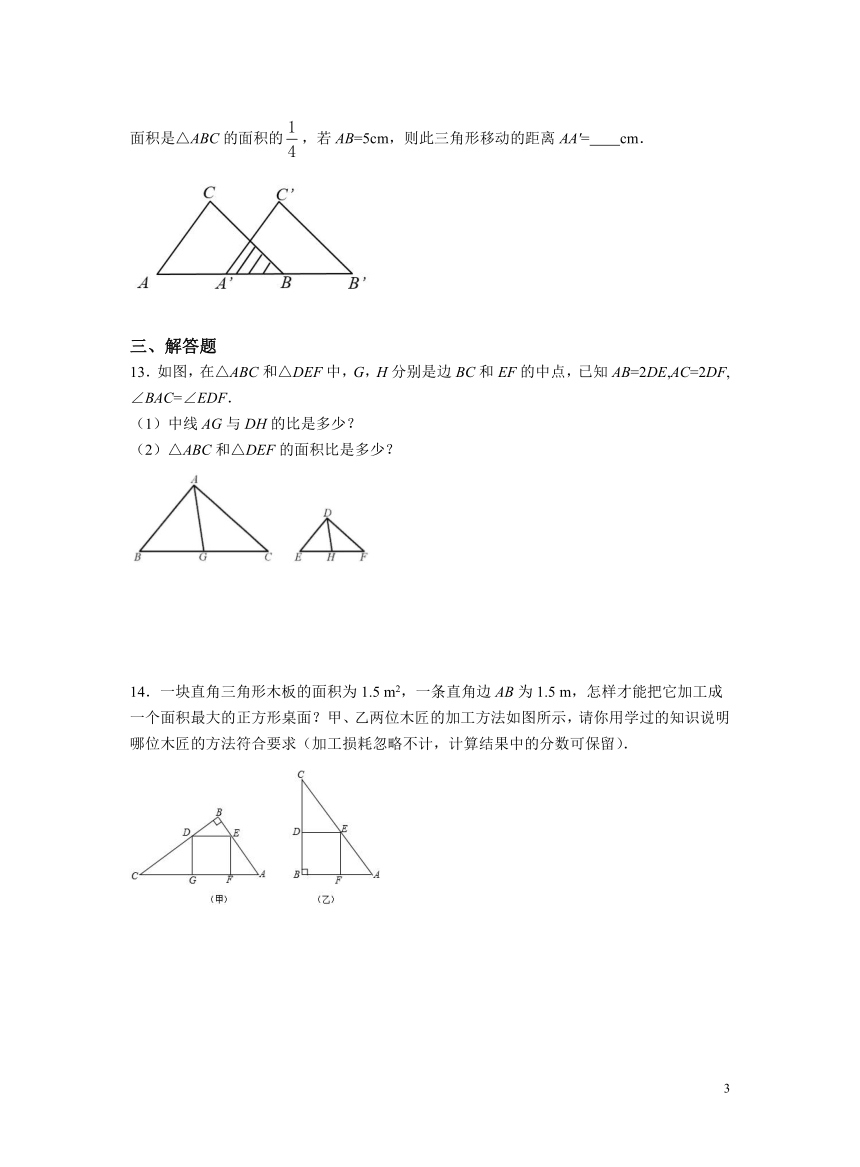
14.一块直角三角形木板的面积为1.5 m2,一条直角边AB为1.5 m,怎样才能把它加工成一个面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用学过的知识说明哪位木匠的方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).
参考答案
1.C
【解析】相似三角形的周长比等于对应的中线的比.
【详解】∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD:A′D′=10:6=5:3.
【点睛】本题考查相似三角形的性质,解题的关键是记住相似三角形的性质,灵活运用所学知识解决问题.
2.C
【解析】直接根据相似三角形面积比等于相似比平方的性质.得出结论:
∵△ABC∽△A'B'C',相似比为1:2,
∴△ABC与△A'B'C'的面积的比为1:4.
3.D
【解析】根据相似三角形的判定与性质进行逐一判断即可.
【详解】解:∵
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
4.C
【解析】由已知证得△ADE∽△AFG∽△ABC,其相似比分别是1:2:3,则面积的比是1:4:9,可求S1:S2:S3=1:3:5.故选:C
5.D
【解析】根据AE:BE=3:1,可得到AE:AB=3:4,再由EF∥BC,可证得
△AEF∽△ABC,从而得到,可得到△AEF=18,即可求解.
【详解】解:∵AE:BE=3:1,
∴AE:AB=3:4,
∵EF∥BC,
∴△AEF∽△ABC
∴
∵, ∴,
∵D是中点, ∴.
6.A
【解析】由△ABC∽△DEF,△ABC与△DEF的面积之比为1:2可知:相似比为1:,则对应中线的比为1:,即可求出答案A.
7.D
【解析】根据图形可得,∠DCP=∠BAP,∠CPD=∠APB进而得出△ABP∽△CDP,根据相似三角形的性质可得,,最后根据CD=3,AB=4进行计算即可.
【详解】解:∵∠DCP=∠BAP,∠CPD=∠APB,
∴△ABP∽△CDP,
∴,故选:D.
【点睛】本题主要考查了相似三角形的判定与性质以及圆周角定理的运用,解题时注意:相似三角形的面积的比等于相似比的平方.
8.D
【解析】分两种情况:①公共部分全在△ABC内;②公共部分的一部分在△ABC内,另一部分在△ABC外.方法一:先利用相似三角形的性质求出PQ在BC边上时x的值,再利用正方形和长方形的面积公式求出y与x的函数关系式即可得;方法二:先利用面积法求出PQ在BC边上时x的值,再利用正方形和长方形的面积公式求出y与x的函数关系式即可得.
【详解】如图,过点A作AD⊥BC于点D,
∵BC=6,
,
解得AD=4,
当PQ在BC边上时,则△AMN的MN边上的高为4-x,
∵MN∥BC
,即
解得x=2.4,
由题意,分以下两种情况:
①当公共部分全在△ABC内,即时,
则y=x2;
②当公共部分的一部分在△ABC内,另一部分在△ABC外,即时,
如图,设AD交MN于E点,且DE=a,则AE=4-a,
∵MN∥BC
即,
解得,
则
由此可知,y与x的函数图象大致是选项D的图象;
【点睛】本题考查了相似三角形的判定与性质、二次函数的图象等知识点,正确分两种情况讨论,并求出临界位置时x的值是解题的关键.
9.8或18
【解析】根据相似三角形面积比等于相似比的平方,求出相似比即可.
【详解】解:∵两个相似三角形的面积比为4:9,
∴两个相似三角形的相似比为2:3,
∴两个相似三角形的周长比为2:3,设另一个三角形的周长为xcm,
则,解得,x=8;或,解得,x=18;
故答案为:8或18.
10.
【解析】根据矩形的性质和勾股定理求出BD,证明△BOF∽△BCD,根据相似三角形的性质得到比例式,求出EF即可.
【详解】解:如图:
∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴EF是BD的垂直平分线,
∴OB=OD=5, ∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
解得,,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90° ,∠EDO=∠FBO
∴EF是BD的垂直平分线,
∴BO=DO,EF⊥BD,
在△DEO和△BFO中,
∴△DEO和△BFO,
∴OE=OF,
.
11.
【解析】根据相似三角形对应中线的比等于相似比求出,根据相似三角形面积的比等于相似比的平方解答即可.
【详解】
解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴
【点睛】本题考查了相似三角形的性质,掌握相似三角形面积的比等于相似比的平方、相似三角形对应中线的比等于相似比是解题的关键.
12.2.5
【解析】由题意易得阴影部分与△ABC相似,然后根据相似三角形的面积比是相似比的平方可求解.
【详解】解:∵把△ABC沿AB边平移到△A′B′C′的位置,
∴∠A=∠D A'B,∠CBA=∠DBA'
∴△ABC∽△A′B′D′,
∵它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的,AB=5cm,
,
;
【点睛】本题主要考查平移性质,相似三角形的性质,熟练掌握平移性质,相似三角形的性质是解题的关键.
13.(1)中线AG与DH的比是2∶1;(2)面积比是4∶1.
【解析】(1)先证明△BAC∽△EDF,推出∠B=∠E,,再证明△ABG∽△DEH,即可求出答案;
(2)根据相似三角形面积的比等于相似比的平方求出答案.
【详解】解:(1)∵AB=2DE,AC=2DF,
∴,
又∵∠BAC=∠EDF,
∴△BAC∽△EDF,
∴∠B=∠E,,
∵G,H分别是边BC和EF的中点,
∴BC=2BG,EF=2EH,
∴,
∴△ABG∽△DEH,
∴,即中线AG与DH的比是2∶1;
(2)∵△BAC∽△EDF,
∴,即△ABC与△DEF的面积比是4∶1.
14.乙木匠的加工方法符合要求.说明见解析.
【详解】
解:作BH⊥AC于H,交DE于M,如图
∵
∴
∵
∴
∴BH=
又∵DE∥AC
∴
∴,解得
设正方形的边长为x米,如图乙
∵DE∥AB
∴
∴
∵
∴乙木匠的加工方法符合要求.
【点睛】本题考查了相似三角形的判定与性质的实际应用及分析、解决问题的能力,正确理解题意,建立数学模型,把实际问题转化为数学问题是解决本题的关键.
答案第1页,共2页
1
一、单选题
1.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )
A.3:5 B.9:25 C.5:3 D.25:9
2.若△ABC∽△A'B'C',相似比为1:2,则△ABC与△A'B'C'的面积的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,△ ABC中,点D、E分别在AB、AC上,且,下列结论正确的是( )
A.DE:BC=1:2 B.△ ADE与△ABC的面积比为1:3
C.△ ADE与△ABC的周长比为1:2 D.DE∥BC
4.如图,△ABC中,DE∥FG∥BC,且AD:DF:FB=1:1:1,则△ABC被分成的三部分面积之比S1:S2:S3=( )
A.1∶1∶1 B.1∶2∶3 C.1∶3∶5 D.1: :
5.如图在△ABC中,点E是AB边上的点,点F是AC边上的点,且EF∥BC,AE:EB=3:1,点D是AE中点,若△ABC的面积为32,则△DEF的面积为( )
A.18 B.12 C.10 D.9
6.已知△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,若BC边上的中线长为1,则EF边上的中线长是( )
A. B.2 C.3 D.4
7.如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么
S△PDC: S△PBA=( )
A.16∶9 B.3∶4 C.4∶3 D.9∶16
8.如图,锐角△ABC中,BC=6,S△ABC =12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MNPQ,设其边长为x,正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
A. B. C. D.
二、填空题
9.两个相似三角形的面积比为4:9,其中一个三角形的周长为12cm,则另一个三角形的周长是________cm.
10.如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD于点E、交BC于点F,则线段EF的长为 __.
11.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若 .
12.如图,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC的面积的,若AB=5cm,则此三角形移动的距离AA'= cm.
三、解答题
13.如图,在△ABC和△DEF中,G,H分别是边BC和EF的中点,已知AB=2DE,AC=2DF,∠BAC=∠EDF.
(1)中线AG与DH的比是多少?
(2)△ABC和△DEF的面积比是多少?
14.一块直角三角形木板的面积为1.5 m2,一条直角边AB为1.5 m,怎样才能把它加工成一个面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用学过的知识说明哪位木匠的方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).
参考答案
1.C
【解析】相似三角形的周长比等于对应的中线的比.
【详解】∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD:A′D′=10:6=5:3.
【点睛】本题考查相似三角形的性质,解题的关键是记住相似三角形的性质,灵活运用所学知识解决问题.
2.C
【解析】直接根据相似三角形面积比等于相似比平方的性质.得出结论:
∵△ABC∽△A'B'C',相似比为1:2,
∴△ABC与△A'B'C'的面积的比为1:4.
3.D
【解析】根据相似三角形的判定与性质进行逐一判断即可.
【详解】解:∵
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
4.C
【解析】由已知证得△ADE∽△AFG∽△ABC,其相似比分别是1:2:3,则面积的比是1:4:9,可求S1:S2:S3=1:3:5.故选:C
5.D
【解析】根据AE:BE=3:1,可得到AE:AB=3:4,再由EF∥BC,可证得
△AEF∽△ABC,从而得到,可得到△AEF=18,即可求解.
【详解】解:∵AE:BE=3:1,
∴AE:AB=3:4,
∵EF∥BC,
∴△AEF∽△ABC
∴
∵, ∴,
∵D是中点, ∴.
6.A
【解析】由△ABC∽△DEF,△ABC与△DEF的面积之比为1:2可知:相似比为1:,则对应中线的比为1:,即可求出答案A.
7.D
【解析】根据图形可得,∠DCP=∠BAP,∠CPD=∠APB进而得出△ABP∽△CDP,根据相似三角形的性质可得,,最后根据CD=3,AB=4进行计算即可.
【详解】解:∵∠DCP=∠BAP,∠CPD=∠APB,
∴△ABP∽△CDP,
∴,故选:D.
【点睛】本题主要考查了相似三角形的判定与性质以及圆周角定理的运用,解题时注意:相似三角形的面积的比等于相似比的平方.
8.D
【解析】分两种情况:①公共部分全在△ABC内;②公共部分的一部分在△ABC内,另一部分在△ABC外.方法一:先利用相似三角形的性质求出PQ在BC边上时x的值,再利用正方形和长方形的面积公式求出y与x的函数关系式即可得;方法二:先利用面积法求出PQ在BC边上时x的值,再利用正方形和长方形的面积公式求出y与x的函数关系式即可得.
【详解】如图,过点A作AD⊥BC于点D,
∵BC=6,
,
解得AD=4,
当PQ在BC边上时,则△AMN的MN边上的高为4-x,
∵MN∥BC
,即
解得x=2.4,
由题意,分以下两种情况:
①当公共部分全在△ABC内,即时,
则y=x2;
②当公共部分的一部分在△ABC内,另一部分在△ABC外,即时,
如图,设AD交MN于E点,且DE=a,则AE=4-a,
∵MN∥BC
即,
解得,
则
由此可知,y与x的函数图象大致是选项D的图象;
【点睛】本题考查了相似三角形的判定与性质、二次函数的图象等知识点,正确分两种情况讨论,并求出临界位置时x的值是解题的关键.
9.8或18
【解析】根据相似三角形面积比等于相似比的平方,求出相似比即可.
【详解】解:∵两个相似三角形的面积比为4:9,
∴两个相似三角形的相似比为2:3,
∴两个相似三角形的周长比为2:3,设另一个三角形的周长为xcm,
则,解得,x=8;或,解得,x=18;
故答案为:8或18.
10.
【解析】根据矩形的性质和勾股定理求出BD,证明△BOF∽△BCD,根据相似三角形的性质得到比例式,求出EF即可.
【详解】解:如图:
∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴EF是BD的垂直平分线,
∴OB=OD=5, ∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
解得,,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90° ,∠EDO=∠FBO
∴EF是BD的垂直平分线,
∴BO=DO,EF⊥BD,
在△DEO和△BFO中,
∴△DEO和△BFO,
∴OE=OF,
.
11.
【解析】根据相似三角形对应中线的比等于相似比求出,根据相似三角形面积的比等于相似比的平方解答即可.
【详解】
解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴
【点睛】本题考查了相似三角形的性质,掌握相似三角形面积的比等于相似比的平方、相似三角形对应中线的比等于相似比是解题的关键.
12.2.5
【解析】由题意易得阴影部分与△ABC相似,然后根据相似三角形的面积比是相似比的平方可求解.
【详解】解:∵把△ABC沿AB边平移到△A′B′C′的位置,
∴∠A=∠D A'B,∠CBA=∠DBA'
∴△ABC∽△A′B′D′,
∵它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的,AB=5cm,
,
;
【点睛】本题主要考查平移性质,相似三角形的性质,熟练掌握平移性质,相似三角形的性质是解题的关键.
13.(1)中线AG与DH的比是2∶1;(2)面积比是4∶1.
【解析】(1)先证明△BAC∽△EDF,推出∠B=∠E,,再证明△ABG∽△DEH,即可求出答案;
(2)根据相似三角形面积的比等于相似比的平方求出答案.
【详解】解:(1)∵AB=2DE,AC=2DF,
∴,
又∵∠BAC=∠EDF,
∴△BAC∽△EDF,
∴∠B=∠E,,
∵G,H分别是边BC和EF的中点,
∴BC=2BG,EF=2EH,
∴,
∴△ABG∽△DEH,
∴,即中线AG与DH的比是2∶1;
(2)∵△BAC∽△EDF,
∴,即△ABC与△DEF的面积比是4∶1.
14.乙木匠的加工方法符合要求.说明见解析.
【详解】
解:作BH⊥AC于H,交DE于M,如图
∵
∴
∵
∴
∴BH=
又∵DE∥AC
∴
∴,解得
设正方形的边长为x米,如图乙
∵DE∥AB
∴
∴
∵
∴乙木匠的加工方法符合要求.
【点睛】本题考查了相似三角形的判定与性质的实际应用及分析、解决问题的能力,正确理解题意,建立数学模型,把实际问题转化为数学问题是解决本题的关键.
答案第1页,共2页
1
